零件的立体视觉测量和三维重建研究

摘 要：本文采用立体视觉测量并结合三维重建的方法，解决了零件的非接触测量问题。首先，分析了立体视觉测量系统的组成结构，利用左、右2个摄像机分别采集零件信息，进而根据二者间的空间关系计算视差数据。其次，采用均值滤波方法去除零件图像噪声，为立体匹配创造条件，进而根据立体图像对二者间的极线关系求取视差。选择Bowyer算法对视差图像进行剖分和三维重建。试验结果表明，本文建立的方法可有效完成航空发动机的叶片零件测量，进而实现生动逼真的三维重建。

关键词：航空发动机；立体视觉；视觉测量；三维重建

中图分类号：TP 39 " " 文献标志码：A

航空发动机的机械构成复杂、零件形状差异性大，导致对其进行测量和缺陷检测等工作具有较大难度。如果采用三坐标测量机类设备测量，需要测头和被测零件进行表面接触，容易导致零件损坏，因此采用无接触的测量方式更可靠。在各种非接触测量方式中，视觉测量是一种常见的测量方法[1]。视觉测量的核心设备是摄像机。将被测零件拍摄图像后，再根据图像处理方法提取特征，完成测量。视觉测量需要光照条件。根据光源的不同，视觉测量又分为结构光测量和自然光测量[2]。结构光测量准确性好，但需要外加结构光源，图像处理过程中需要结构光编码和解码，复杂程度较高。自然光测量无须外加光源。测量过程中，根据摄像机的数目不同，又可以分为单目视觉测量、双目视觉测量、多目视觉测量[3]。其中，双目视觉测量利用2个摄像机的空间几何关系计算出被测物的深度信息，进而根据重建方法完成被测物的三维重建。本文即采用双目立体视觉测量和三维重建结合的方法对航空发动机的零件进行测量和重建。

1 基于立体匹配的深度测量

在各种机器视觉技术中，双目立体视觉具有非常重要的地位。双目立体视觉技术最早由美国麻省理工学院人工智能实验室的Marr博士提出，他从2幅有视差的平面图像中提取出三维信息，奠定了双目立体视觉发展的理论基础。双目立体视觉系统中的2个摄像机对应人类的左、右眼。从仿生学的角度来看，双目立体视觉系统是人类视觉系统在机器人上的再现，是实现机器人类人智能的一种最直接的手段。双目立体视觉技术发展到今天，已经成为视觉测量领域的一个主要研究方向。

双目立体视觉技术从平面图像提取三维信息的过程类似用人眼观测周围环境的过程。人眼最终还可以把采集的信息在视网膜上重现，而双目立体视觉技术要想把提取出的三维信息复原为原始景物，就需要借助三维重建技术。双目立体视觉测量的基本原理如图1所示。

图1中，左、右2个摄像机共同拍摄一个场景区域，根据二者间的空间位置关系对同一点进行视差计算。视差最终可以恢复被测点的深度信息，从而获得被测物的完整三维信息。

由于摄像机在测量过程中会受各种干扰，因此左、右摄像机拍摄的图像需要进行去噪处理才能进一步用于视差计算。本文采用均值滤波去除图像中的噪声。去噪过程中使用的2个模板如图1所示。

首先，用模板一搜索图像中的随机噪声。用f（x，y）表示原始图像中的像素灰度，模板的中心点f（1，1）即待搜索的像素。其次，求出模板内的灰度均值，如公式（1）所示。

（1）

式中：表示灰度均值；f（x，y）表示图像中位于（x，y）的像素灰度。

然后计算与f（1，1）的差值，并将此差值与预先设定的阈值α进行比较。α根据图像像素灰度值矩阵的统计结果对进行人为设定，在不同的试验条件下，α取值也不同，此处将α设定为10。

如果与f（1，1）的差值小于阈值α，即差异在10个亮度等级内，就可认为该像素不是随机噪声；如果该差值大于阈值α，即差异大于10个亮度等级，可认为该像素是随机噪声，用模板二对该像素进行处理，如公式（2）所示。

（2）

式中：f（x，y）表示图像中位于（x，y）的像素灰度；f（1，1）表示模板中位于中心点的像素灰度，即在位置（1，1）上的像素灰度。

然后用f1（1，1）代替f（1，1），即可去除随机噪声。由此图像灰度由f（x，y）变为f1（x，y）。

本文采用的均值滤波经过特定模板的处理，能更有针对性地处理随机噪声，进一步增强图像质量。由试验还可知，本文提出的均值滤波对某些由规律电磁干扰造成的椒盐噪声和高斯噪声也具有一定处理能力，从而使去噪效果超出预期。因此，使用本文的均值滤波可显著改善图像质量，为左、右图像间对应图像特征的搜索识别乃至匹配奠定了基础。采用本文均值滤波方法去噪后，如果双目立体视觉系统已经标定，同时采集后的图像经过外极线校准和预处理，则可以执行进一步的立体匹配。

经过外极线校准后，左、右2幅图像满足外极线约束条件，即左、右2幅图像中对应的匹配点必在同名极线上。假定图像宽度为w，最大搜索视差为dmax。现在取出左、右2幅图像上的一组同名极线xL和xR，以右极线xR上一点xRi（0≤i≤w）为参考点，依次与左极线xL上n（n=dmax）个点xLj（i≤j≤i+dmax）进行相似性测度计算，即可得到n个匹配代价。遍历整个图像时，就可以得到三维的视差空间图像。进而用多种相似性测度计算视差空间图像中的匹配代价，如公式（3）所示。

（3）

式中：W（）代表相似性测度函数；wx代表匹配窗口的横坐标；wy代表匹配窗口的纵坐标；cx代表匹配窗口中心点的横坐标；cy代表匹配窗口中心点的纵坐标；IR代表左侧图像灰度；IL代表右侧图像灰度；MR代表左侧图像匹配代价；ML代表右侧图像匹配代价。

2 基于深度信息的三维重建

三维重建技术是计算机图形学的重要分支，其技术实现过程是充分利用输入的点云信息及其空间几何位置关系，在剖分、拟合、多边形拼接、面片生成、光照渲染和材质设定等技术手段的支持下，复原被测物三维形貌的过程。自出现以来，三维重建在很多领域均得到了广泛应用，包括人工智能的虚拟现实领域、工程建造的BIM信息化建模领域以及医学辅助手术治疗的虚拟导引领域。

如果将测量和重建看成完整的技术体系框架，那么立体视觉测量和三维重建分别位于不同的技术环节，并按照密切相关的先后顺序衔接。对一个被测物体进行三维测量和复原时，可以采用立体视觉进行表面拍摄，进而从图像信息生成视差信息，再生成三维点云信息。三维点云信息作为输入进入三维重建环节，用于进一步的三维形貌复原。可见，立体视觉环节的测量结果恰好是三维重建环节的输入。

对于三维重建的实用性要求，在目前很多领域的研究中，实现三维表面重建就可以满足要求。而三维空间中曲面的重建方法大体可分为整体拟合和局部拟合2类，其中局部拟合是主流技术。局部拟合一般利用多边形连接技术，从某一局部构建最初的多边形，然后再根据某些准则向外扩展，连接新的点以构成新的多边形。直到所有数据被连接完毕，再用这些网格生成面片，最终重建出曲面。而在所有多边形剖分中，三角形是最常用的。

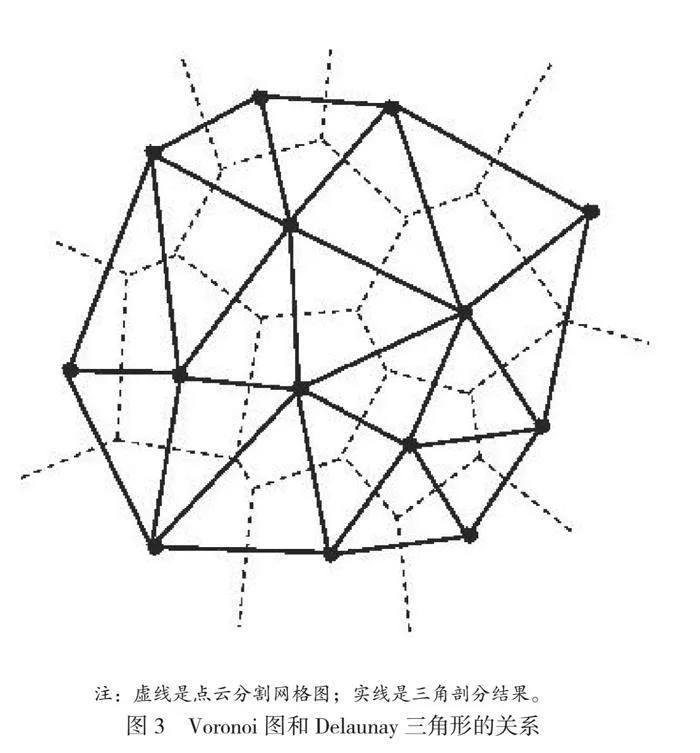
三维曲面具有整体面积大、复杂程度高的特点，会给复原和重建工作带来较大困难，一般都不采用整体重建的策略，而采用小范围剖分、再连接成整体的重建思路，因此剖分就成为三维曲面重建的关键技术。剖分又分为三角形剖分和多边形剖分。其中三角形剖分具有局部最小的剖分分辨率，实现技术难度低、剖分效果好且速度快。三角剖分的一种最简单的实现手段就是将参与剖分的点云从三维空间向二维平面投影，先在二维平面进行剖分成型后，再加入各点的深度信息并反映射回三维空间，例如Bowyer算法。但三维点云存在空间上的重叠或交错，直接的平面剖分可能会出现误差。在三角剖分中，直接根据特定的规则在三维空间中完成立体剖分也是一种常见的思路，例如Waston算法，即直接根据点云数据生成Voronoi图，再根据Voronoi图进行Delaunay三角形的划分。Voronoi图和Delaunay三角形的关系如图3所示。

从图3的三角剖分结果可以看出，在Bowyer算法中，三维点云被剖分成细密的三角形网格，剖分结果均匀。三维物面的点云数据采用剖分三角处理后，形成多个彼此连接的三角面片。这些面片经过光照处理就可以逼真地复原出原始物体的三维形貌特征。剖分出的三角形越接近正三角形、剖分数量越细密，三维重建的效果越理想。

本文采用Bowyer算法三角剖分法完成三维重建。Bowyer算法是典型的二维平面投影剖分算法。在三维点云完成向二维平面投影后，直接在平面内进行三角剖分，然后再恢复到三维空间中生成空间剖分结果。从算法的技术实现过程来看，该算法属于典型的递归剖分。Bowyer算法的实施步骤如下。

第一步，将三维空间点云投影到二维平面，并根据二维点云的区域面积构建初始三角形，该初始三角形应该涵盖平面内的所有点。

第二步，在初始三角形靠近中心的位置选择一个点进行第二次剖分，经过第二次剖分，初始三角形会形成3个新的三角形。

第三步，再以每个新的三角形为剖分标的，分别在其内部选择一个靠近中心位置的点，对每个新的三角形进行剖分，又分别形成3个更新的三角形。至此，已经得到9个三角形。

第四步，按照上述步骤，继续剖分每个新的三角形，直到原始点集中的点全部被使用完毕。

3 叶片零件的三维重建试验

为了验证本文提出的立体视觉测量方法和三维重建方法的有效性，本文针对航空发动机叶片进行视觉测量和重建试验研究。运用立体视觉方法测量航空发动机叶片，得到的三维点云数据结果如图4所示。

从图4可以看出，通过本文建立的立体视觉测量方法得到的航空发动机叶片点云数据十分稠密且均匀，为后续的三维重建奠定了基础。从形态上看，航空发动机叶片的三维点云数据空间分布均匀、相邻点各向间隔距离均衡，由此重建出的发动机叶片效果将更细腻和光滑。

对图4中的点云数据进一步执行Bowyer算法，得到三角剖分后再施加光照，得到航空发动机叶片的三维重建结果，如图5所示。

图5为3个不同角度的叶片三维重建结果，并施加环境光照以增强视觉效果。从图5的结果可以看出，运用Bowyer算法进行三维重建并复原的三维形貌特征，基本复原了真实叶片，对后续处理具有很强的支撑作用，例如叶片缺陷识别、叶片重塑的逆向工程等。

4 结论

我国航空工业取得了飞速发展，航空发动机的需求也日益扩大。对航空发动机关键零部件进行测量是确保航空发动机品质的重要保证。本文在机器视觉测量技术的基础上，采用基于双摄像机的立体视觉测量技术，对航空发动机叶片进行视觉测量。获得叶片上每个点的视差信息后，再根据空间几何位置关系复原具有深度信息的叶片点云数据。最后根据Bowyer算法对叶片三维点云数据进行三角剖分和三维重建。试验结果显示，Bowyer算法取得了非常理想的叶片三维重建效果。本文建立的立体视觉测量和三维重建方法体系，对航空发送机的零部件检测具有十分重要的意义。

参考文献

[1]王洪君，孙筱雯，石钧.基于自适应邻域对比度增强的直方图均衡算法[J].计算机应用，2023，23（1）：124-126.

[2]朱松立，戴礼荣，宋彦，等.基于角点特征值和视差梯度约束的角点匹配[J].计算机工程与应用，2022，34（6）：6-8.

[3]史松伟，任秉银.三维稀疏散乱点集的直接三角剖分新方法[J].哈尔滨工业大学学报，2022，37（10）：1318-1320.