新能源项目智能监控系统在后期运维中的应用

摘 要：本研究的目标是利用层次分析法（Analytic Hierarchy Process，AHP）和熵值法构建一个全面的评价体系，以评估新能源项目智能监控系统在后期运维中的效益。考虑在实际运营过程中数据的稀缺性，在评估过程中引入Bootstrap方法。Bootstrap方法利用重复抽样构建多个虚拟样本，优化模型的预测性能。为评估监控系统的效益，进行Bootstrap采样分析，将采样分布结果与原始数据进行对比。这种方法能够更全面了解系统性能，准确评估后期运维效益。本研究旨在为新能源项目的智能监控系统提供科学、可靠的评估框架，优化运营系统，提升可持续性。

关键词：新能源项目；智能监控系统；效益评估；Bootstrap方法

中图分类号：X 924 " " " " 文献标志码：A

在新能源领域，智能监控系统在提高系统性能、降低运维成本方面起到了关键作用，因此备受关注。成建国等[1]（2023）深入研究了深圳城际动车组智能化需求以及顶层指标建议方案，提出了创新的智能化方案，为城际动车组运营提供了新思路。樊任璐[2]（2023）研究上海轨道交通1号线空调智能运维系统。陈泽涛等[3]（2022）研究配电房安全智能监控平台接地刀闸状态位监控方法。钟怡然等[4]（2022）从现有智能监控系统中发展了三维建模技术并将其应用于安防领域。谈震等[5]

（2022）研究水利工程智能运维全链路监控系统。王学文等[6]（2022）研究AR/VR融合驱动的综采工作面智能监控关键技术。刘海滨等[7]（2018）研究水电站智能监控服务支持系统，为水电站提供全面的监控服务。于闯等[8]（2018）研究了动车组转向架智能监控分析平台。姜国义等[9]（2016）研究基于网络技术的信息系统集成接口智能监控管理，为企业信息系统集成管理提供了有效手段。

1 算例分析

1.1 变量选取

在能源领域中的重要任务是评估新能源项目智能监控系统在后期运维中的效益。为了更全面、客观地了解该系统的效用，本文采用AHP-熵值法结合专家评测的方法，确定技术可行性、系统性能和运维需求这3个关键准则的权重，进而深入评估其在后期运维中的作用和影响。

在新能源项目中，智能监控系统在后期运维中的效益十分重要。为了准确评估其效益，引入AHP-熵值法。这个方法结合了层次分析法（Analytic Hierarchy Process，AHP）和熵值法，能够在多个准则间建立层次结构，确定各准则的权重，综合分析系统的整体效益。本文的目标是评估智能监控系统的效益，涉及技术可行性、系统性能和运维需求这3个关键准则。技术可行性指系统所采用的技术是否适用于特定情况，系统性能考量系统的整体工作表现，运维需求关注系统后期维护所需的资源和投入。

为了确定这些准则的相对重要性，由专家进行评估，并采用两两比较的方法。向专家提供问卷，引导专家对这3个准则进行比较，使用1～9的尺度确定其相对权重。这些比较结果构成比较矩阵，作为计算权重的依据。例如，专家将技术可行性和系统性能进行比较，给出1～9的评分。

本研究结合专家经验与定量分析，对比较矩阵进行一致性检验和特征值计算，得到各准则的权重向量。这些权重向量是基于专家评估的定量化结果，代表不同准则在系统效益中的相对重要性。

1.2 重要性对比

向专家提供问卷，进行两两比较，确定准则之间的相对重要性，计算相应的权重。这些权重将应用于熵值法中，以综合各准则的信息熵，确定最终的权重分配。

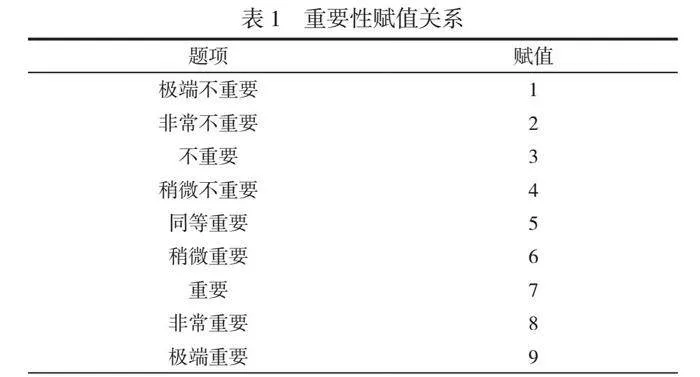
专家完成两两比较矩阵，使用尺度1～9，其中，1为相同重要性，9为极端重要性，重要性赋值关系见表1。

本文采用分析方法并借鉴了专家的经验，使新能源项目智能监控系统的效益评估更详尽、可靠。将问卷调查与专家评测相结合，从而建立科学、全面的评估框架，在后期运维中能够更精准地评估系统的综合效益。重要性评估结果见表2。

这些重要性评估结果是对智能监控系统准则间相对重要性的量化。在未来的研究中，基于这些结果进一步探索在不同权重中系统效益的变化情况，以及在不同假设权重中系统整体性能的变化趋势，进一步优化智能监控系统。

1.3 AHP-熵值法权重估计

在AHP-熵值法中，AHP方法将专家的两两比较转化为特征向量，计算各准则的权重。在这个过程中，根据两两比较矩阵获得了特征向量，该向量代表各准则相对重要性的度量。对特征向量进行归一化处理，得到初始的权重向量。计算一致性指标（CI）和一致性比率（CR），验证权重向量的一致性和可信度。

根据计算得到的CR与预设一致性水平进行对比，如果CR较低，则所得权重相对可信；如果CR较高，则需要重新考虑比较矩阵的一致性。结合初步的权重向量调整一致性比率，最终确定了准则的权重。专家判断层次结构中的每对准则，得到了两两之间的比较矩阵Cij。这些矩阵构成了层次结构的判断矩阵。基于上述重要性评价结果，计算得到CI=0.03，CR=0.10。

对每个比较矩阵进行归一化处理，得到权重向量Wi和对应的最大特征值λi。根据归一化的特征向量得到初始的准则权重W。

进行全局一致性检验后，使用特征值法计算得到最终的权重向量，见表3。

AHP-熵值法将AHP的权重评估与熵值法的信息熵相结合，获得最终的权重分配。这种方法使专家评估的权重在综合信息熵后更可靠、合理。对比较矩阵进行归一化处理，得到权重向量。利用这些权重向量，按照信息熵的计算公式计算每个准则的熵值，熵值越大，准则内部的差异性越高，即不确定性程度越大，如公式（1）所示。

（1）

式中：Ei为信息熵；Cij为准则i与j之间两两比较重要性结果的矩阵；λi为这个重要性矩阵的最大特征值；n为这个重要性矩阵的阶数。

熵权重Wentropy，i计算过程如公式（2）所示。

（2）

综合初始权重和熵权重得到最终权重W'。这个过程结合了专家评估意见与量化信息熵，保证权重的科学性和客观性。计算过程如公式（3）所示。

W'=α·W+（1-α）·Wentropy，i " "（3）

式中：W'为最终权重；α为权衡初始权重和熵权重的权衡因子，取值为0.5；W为基于AHP法计算的准则权重；Wentropy，i为基于熵值法计算的熵权重。

融合AHP与熵值法的方法考虑了专家评估和准则内部的差异性，在AHP权重计算中引入更多的数据特性，更好地反映准则之间的相对重要性，为评估体系提供了更全面、可靠的权重分配，为智能监控系统的后期运维效益提供支持。

1.4 权重优化过程

根据计算得到熵值，利用信息熵概念进行进一步优化权重，熵权重的计算考虑了信息熵的影响，修正并优化了初始权重，使权重更合理。

计算各准则的熵值，进一步优化权重。优化后的权重见表4。

在新能源项目中，对技术可行性、系统性能以及运维需求等关键准则进行评估，其熵值分别为0.97、0.72和0.81。这些熵值反映了不同准则内部信息的复杂程度和不确定性，为后续权重调整提供依据。利用基于层次分析法的特征值法计算熵权重，得到修订后的权重分配，即A准则的熵权重为0.273，B准则的熵权重为0.499，C准则的熵权重为0.228。这些熵权重是对初始权重的修正和优化，更准确地反映了每个准则在系统效益评估中的重要性。例如，在智能监控系统中，系统性能在整体评估中占主导地位，技术可行性和运维需求的重要性不高。

1.5 Bootstrap方法

Bootstrap方法是一种重要的数据增强技术，在解决数据不足的问题方面起到关键作用。它多次有放回地从原始数据中进行抽样，生成多个虚拟样本集合，从而增加样本量。因为这种方法有助于提高模型的预测性能与鲁棒性，所以在新能源项目监控系统的效益评估中十分重要。

假设本文有1个包括N个样本的原始数据集A，如公式（4）所示。

A={x1，x2，…，xN} （4）

式中：x1为样本，1～N为样本个数。

针对每个虚拟样本集合，利用建立的AHP评价体系计算相应的效益得分，这些得分反映了每次重抽样构成的虚拟样本在评估体系中的效益。本文从原始数据集中有放回地随机抽取N个重抽样的样本，构成1个虚拟样本集合，如公式（5）所示。

A={x1'，x2'，…，xN'} （5）

式中：x1'为x1的重抽样样本。

对每个虚拟样本X'，本文使用构建的AHP评价体系，计算得到相应的效益得分，如公式（6）所示。

Y'=f（X'） " " " " " （6）

式中：Y'为重抽样后的效益得分。

统计所有重抽样样本的效益得分，得到更全面的评估结果。生成了B个虚拟样本，B为Bootstrap的次数。得到M个效益得分，如公式（7）所示。

Y∈{y1'，y2'，…，yM'}，{y1'，y2'，…，yM'}∈B " " （7）

式中：Y为效益得分的样本集合；y1'，y2'，…，yM'为其他重抽样样本。

本文对重抽样样本进行多次评估，计算效益得分的均值、方差等统计量，了解样本之间的变化范围，减少了样本不确定性对效益评估结果的影响。引入Bootstrap方法，根据计算效益得分的分布情况来评估体系对数据变动的鲁棒性，从而更全面地了解模型在不同数据分布中的表现。

2 结果与讨论

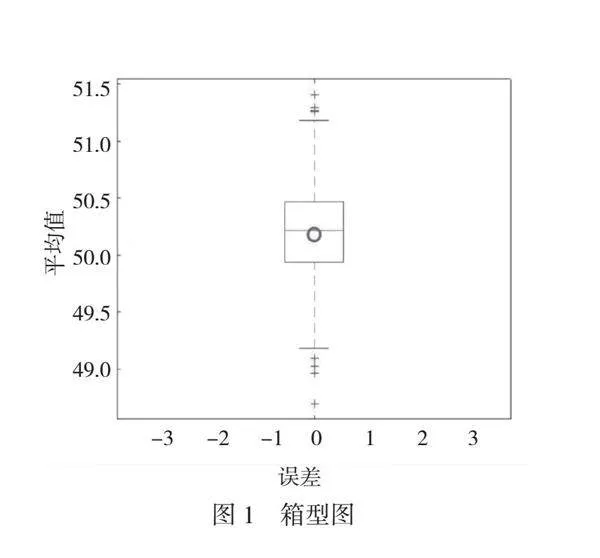
本文对Bootstrap采样分布和原始数据进行对比，可以全面了解效益评估的不确定性。通过计算均值、置信区间等统计量，可以评估监控系统的性能。其结果如图1所示。

使用箱型图呈现了Bootstrap方法的效果，箱型图显示了不同采样分布中的数据分布情况，利用这种方式可以直接观察Bootstrap采样分布与原始数据之间的差异。

采样分布与单一样本方法之间的差异如图2所示。引入Bootstrap方法在极小样本规模中对监控系统的效益进行优化评估。对比分析结果显示，Bootstrap采样分布与单一样本方法相比更稳健，说明Bootstrap方法在解决数据不足问题方面更有优势，效益评估结果更可靠。箱型图和柱状图都展现了与正态分布相似的趋势，该趋势共同反映了效益评估的结果相似。这些结果强调了在新能源项目智能监控系统效益评估中，Bootstrap方法在数据样本较少的情况下效益评估可靠、有效。

尽管结果呈现相似趋势，但是需要注意采样分布与单一样本方法之间的差异可能受到多种因素影响。样本容量、采样方法以及数据分布等因素可能会对2种方法的评估结果产生影响，导致评估结果之间出现微小差异。虽然Bootstrap方法展现了在小样本数据方面的优势，但是研究者在使用这种方法的过程中需要考虑数据采样的多样性和适用性，在特定情况下最大程度地提高Bootstrap方法的效益。未来研究可以进一步探索Bootstrap方法在不同条件下的稳定性，以及在数据不足的情况下对效益评估结果的影响程度。深入分析将有助于了解Bootstrap方法在智能监控系统效益评估中的应用潜力，为后续类似问题的研究提供更丰富的经验。

3 结论

采用AHP和熵值法构建评价体系，利用Bootstrap方法优化效益评估的预测性能，本研究为新能源项目的智能监控系统提供一种全面、稳健的评估方法。未来研究可以进一步扩大样本规模，引入更多影响因素，提高评估准确性，完善评估体系。探索更先进的评价方法和模型，结合机器学习等技术提高预测性能。案例分析和实证研究能够验证评价体系的实用性，为全面决策提供更可靠的评估指标。这些研究将优化监控系统评估方法，助力新能源领域可持续发展。

参考文献

[1]成建国，张桂南，郭晓燕，等.深圳城际动车组智能化需求及顶层指标建议方案研究[J].铁道运输与经济，2023，45（7）：110-118.

[2]樊任璐.上海轨道交通1号线空调智能运维系统[J].城市轨道交通研究，2023（增刊1）：128-131，136.

[3]陈泽涛，王增煜，刘秦铭，等.配电房安全智能监控平台接地刀闸状态位监控方法研究[J].电网与清洁能源，2022，38（12）：95-100，106.

[4]钟怡然，胡迪，俞肇元，等.基于多粒度时空对象数据模型的高速公路智能监控系统建模[J].地理与地理信息科学，2022，38（1）：110-115.

[5]谈震，舒依娜，刘敏，等.水利工程智能运维“云-网-端”全链路监控系统的研究与设计[J].中国农村水利水电，2022（9）：19-24，29.

[6]王学文，刘曙光，王雪松，等. AR/VR融合驱动的综采工作面智能监控关键技术研究与试验[J].煤炭学报，2022，47（2）：969-985.

[7]刘海滨，董海洋，秦晓康，等.水电站智能监控服务支持系统研究与应用[J].水电能源科学，2018，36（8）：162-165，213.

[8]于闯，高明亮，邵俊捷，等.动车组转向架智能监控分析平台研究[J].城市轨道交通研究，2018，21（2）：67-71.

[9]姜国义，郭宝财.基于网络技术实现信息系统集成接口智能监控管理[J].企业管理，2016（增刊2）：508-509.