基于LSTM-AEKF算法的锂离子电池SOC估计

摘 要：针对扩展卡尔曼滤波（Extended Kalman filter，EKF）算法与长短期记忆网络（Long Short-Term Memory，LSTM）不能准确估计锂离子电池荷电状态（State of Charge，SOC）的问题，本文提出了一种基于二阶戴维宁（Thevenin）的等效电路模型，采用自适应扩展卡尔曼滤波（Adaptve Extended Kalman filter， AEKF）与LSTM相结合的SOC估计算法，即LSTM-AEKF算法。在二阶RC等效电路模型的基础上建立整数阶模型，并采用EKF算法辨识模型参数，采用LSTM-AEKF算法估计SOC，与AEKF算法、LSTM算法进行比较。根据马里兰大学公开数据集进行测试，结果表明，与传统方法相比，LSTM-AEKF算法估计SOC的平均绝对误差（Mean Absolute Error，MAE）与均方根误差（Root Mean Square Error，RMSE）分别下降了1.23%、1.5%，基于二阶RC模型的LSTM-AEKF算法可以有效估计SOC。

关键词：锂离子电池；SOC估计；二阶Thevenin等效模型；长短期记忆网络（Long Short-Term Memory，LSTM）；自适应扩展卡尔曼滤波

中图分类号：TM 912 " " " " " " 文献标志码：A

锂电池的SOC（State of Charge）即锂电池目前的剩余电量，SOC取值为0%～100%，当SOC为100%时，表示完全充满电；当SOC为0%时，表示电池剩余电量为0，电池的内部电量完全放空。电池SOC的测量受外界因素和电池内部因素影响，对电池进行SOC精确估计十分重要。

目前，SOC估计方法主要有3种，分别为安时积分法、长短期记忆网络（Long Short-Term Memory，LSTM）相关算法和卡尔曼滤波相关算法[1]。安时积分法是一种计量电池电量的基础方法，它采用安时（Ampere-Hour，AH）累积的方法，对锂电池进行实时SOC估计[2]。LSTM算法估计非线性系统效果较好，但是在利用LSTM算法估计SOC的过程中，得到的解不一定是全局最优解[4]。在实践中，扩展卡尔曼滤波（Extended Kalman filter，EKF）算法是一种常用算法，可以较好地估计非线性系统的SOC问题[5]。

针对在不同噪声环境中，EKF算法对SOC估计精度不足的问题，本文将自适应扩展卡尔曼滤波（Adaptve Extended Kalman Filter，AEKF）与LSTM相结合，得到LSTM-AEKF 算法，该算法在鲁棒性较高的情况下避免了得不到全局最优解的问题，提升了SOC的估计精度。

1 建立二阶等效电路模型与在线参数辨识

1.1 建立等效电路模型

与低阶RC电路模型相比，高阶RC电路模型能够更准确地模拟电池的动态特性。由于高阶模型涉及复杂的计算，因此，为了在精度与计算复杂度之间取得平衡，本文选择二阶RC模型。二阶RC等效电路模型由开路电压、电阻和2组RC网络组成，如图1所示。

二阶RC等效电路的状态方程如公式（1）所示。

（1）

式中：t为当前时刻；U1、U2为2个RC回路的电压；R1、R2为电阻器；C1、C2为极化电容；IT为负载电流；Qn为电池容量；SOC为电池SOC初始值。输出方程如公式（2）所示。

UL=UOC（SOC）-R0IT-U1-U2 " " " " " " " " " " " （2）

式中：UL为端子电压；R0为欧姆内阻；UOC（SOC）为锂电池开路电压关于SOC的拟合多项式。

二阶RC模型建立完成后，须辨识锂电池内部参数，待辨识的参数包括开路电压 UOC，电路中的电阻R1、R2，电容 C1、C2以及欧姆内阻R0[3]。

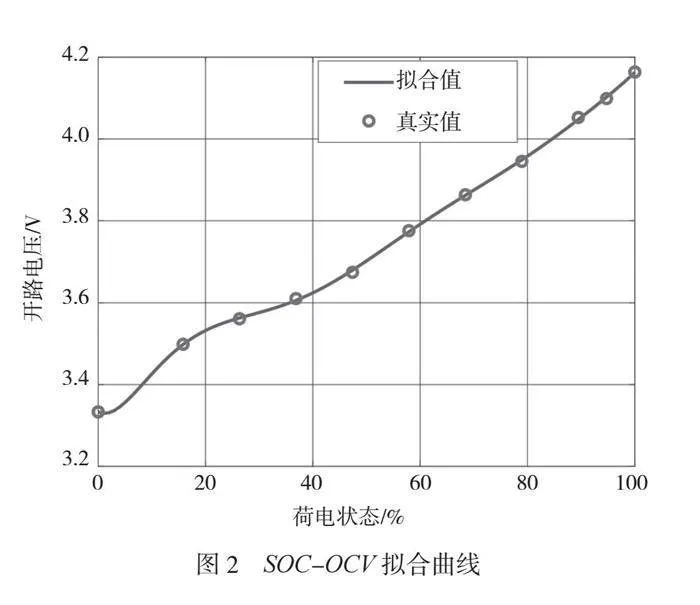
利用曲线拟合识别 UOC（SOC）[6]。使用马里兰大学锂电池试验的公开数据集数据，放电电流脉冲为1 A，放电电流持续时间为720 s，导致SOC下降了10%。当每次电池放电时，将其静置2 h，以保证端电压约等于开路电压。使用八阶多项式来精确拟合测量数据，如公式（3）所示。

UOC（SOC）=-170.24SOC8+665.92SOC7-

1 048.60 SOC6+851.71SOC5-384.83SOC4+

102.49SOC3-18.66SOC2+3.07SOC+3.264 2 " " （3）

SOC-OCV拟合曲线如图2所示。

1.2 在线参数辨识

离线参数辨识不能辨识所有电池工况，无法保证参数辨识的准确性[11]。当实际运行时，锂电池内部化学反应十分复杂，在线参数辨识能够精确辨识锂电池内部参数。锂电池在线参数辨识以电池的工况数据为基础，利用算法实时更改电池参数，追踪电池的实际工作状态[12]。本文采用卡尔曼滤波算法[7]辨识电池等效电路模型参数。二阶RC等效电路模型的在线参数辨识结果如图3所示。

2 AKEF与LSTM

LSTM-AEKF算法的核心是先使用LSTM算法估计电池SOC，得到1个SOC初始值，再使用AKEF算法[8]对估计结果进行二次修正，提升了SOC的总体估计精度。

2.1 使用LSTM进行SOC估计

LSTM的隐含层在循环神经网络（Recurrent Neural Network，RNN）的基础上增加1个细胞状态（Cell State）用于保存长期状态。引入该细胞状态可以有效解决RNN中存在的问题。

LSTM的结构如图4所示。LSTM和RNN采用相同的链式结构，RNN的隐含层中只有1个简单的tanh结构，LSTM包括4个结构，这4个结构采用特殊的方式进行交互[9]。LSTM增加的结构为门结构，包括遗忘门、输入门和输出门，可以选择性通过数据信息。

安时积分法估计SOC的计算过程如公式（4）所示。

（4）

式中：SOC0为初初始值；i（t）为t时刻的电流值。本文将电池电压、电流以及在线辨识得到的R0、R1、R2、C1和C2、作为输入数据，并将由公式（4）计算得到的SOC真实值中的90%作为训练集，模型训练完成后，其余10%作为预测集，调用已训练的LSTM完成SOC的估计，与SOC真实值进行比较，记录由LSTM估计得到的SOC与SOC估计误差。

2.2 使用AKEF进行SOC估计

噪声方差会影响卡尔曼滤波估计的准确性，不准确的噪声方差会导致估计精度降低，甚至导致滤波发散。假设过程噪声协方差矩阵Q和测量噪声协方差矩阵R是常数，那么对卡尔曼滤波估计SOC来说，这种根据经验和随机性得到的Q和R并不适用。而且，参数随SOC的估计进程实时改变。为了获得随估计过程而变化的Q值和R值，本文引入自适应思想。自适应思想即实时改变Q和R的数值，使其能够适应系统的SOC估计，得到高估计精度。本文将第2.1节估计得到的SOC值作为SOC初始值，在线辨识得到的电池参数R0、R1、R2、C1和C2，使用AEKF算法来获得更准确的SOC估计结果[10]。AEKF算法计算过程如公式（5）～公式（12）所示。

初始化状态向量如公式（5）所示。

x=[U1，U2，SOC]T " " " " " " " " " "（5）

式中：x为初始化系统的状态向量。

利用电池模型进行状态预测，如公式（6）所示。

=f（xk，uk） " " " " " " " " " （6）

式中：f（xk，uk）为状态方程；为预测的状态向量；xk为上一个时刻的状态向量；uk为输入。

状态预测误差协方差矩阵计算过程如公式（7）所示。

=AkPkAkT+Qk " " " " " " " （7）

式中：为更新后的状态误差协方差矩阵；Pk为当前时刻的状态误差协方差矩阵；Ak为状态转移矩阵；Qk为过程噪声协方差矩阵。

观测预测误差协方差矩阵计算过程如公式（8）所示。

Sk=Hk+1Rk+1 " " " " " " （8）

式中：Sk为观测误差协方差矩阵；Hk+1为观测矩阵；Rk+1为测量噪声协方差矩阵。

计算卡尔曼增益，更新状态协方差矩阵，如公式（9）、公式（10）所示。

（9）

Pk+1=（I-Kk+1Hk+1） " " " " " " （10）

式中：Kk+1为计算后的卡尔曼增益；S-1 k+1为更新后的观测误差协方差矩阵；Pk+1为更新后的状态协方差矩阵；I为单位矩阵。

状态测量与误差协方差更新如公式（11）、公式（12）所示。

xk+1=+Kk+1（zk+1-h（）） " " " " " " " " " " " "（11）

Pk+1=Pk+1-Kk+1Hk+1 " " " " " " " " " " " " （12）

式中：zk+1为测量值；h为观测方程。SOC的估计值从更新后的状态向量xk+1中提取；Kk+1（zk+1-h（））为计算后的卡尔曼增益值乘以测量值与观测值的差值。

3 试验结果与分析

试验中使用的数据为马里兰大学公开数据集，试验中使用的电池型号为INR 18650-20R。电池的标称电压为3.6 V，容量为2 Ah，试验温度为25 ℃，采样间隔为1 s。

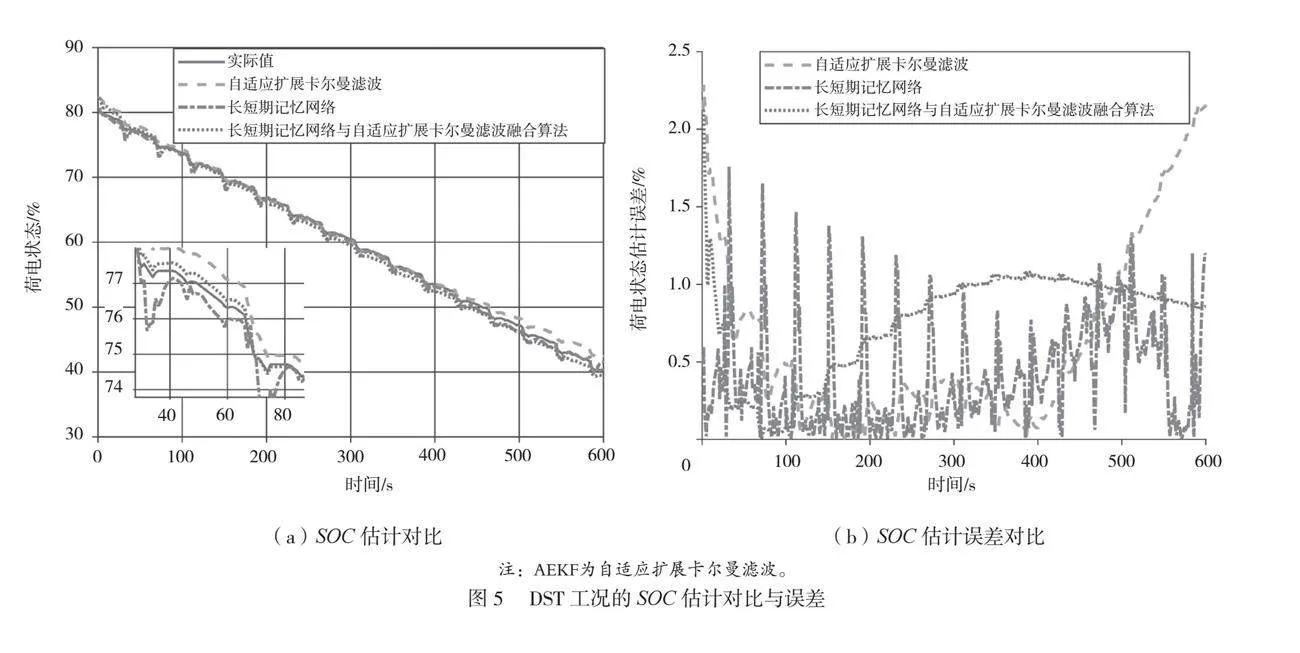
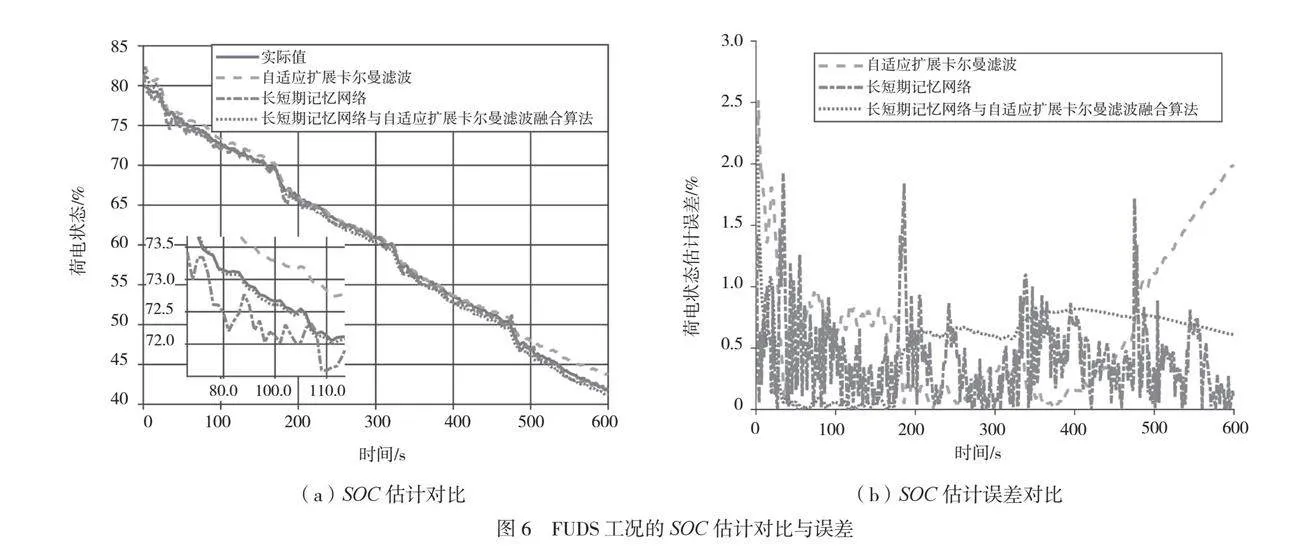
为了验证LSTM-AEKF算法在不同工况中的可推广性，使用DST、FUDS 2种不同工况数据进行SOC估计，将估计结果分别与AEKF算法和LSTM算法进行比较。试验结果和误差分别如图5、图6所示。从图5、图6可以看出，AEKF算法、LSTM算法和LSTM-AEKF算法可以有效地估计SOC，LSTM-AEKF算法的估计结果更接近真实值。与AEKF和LSTM算法相比，LSTM-AEKF算法的估计误差更低，在不同工况中波动更小。

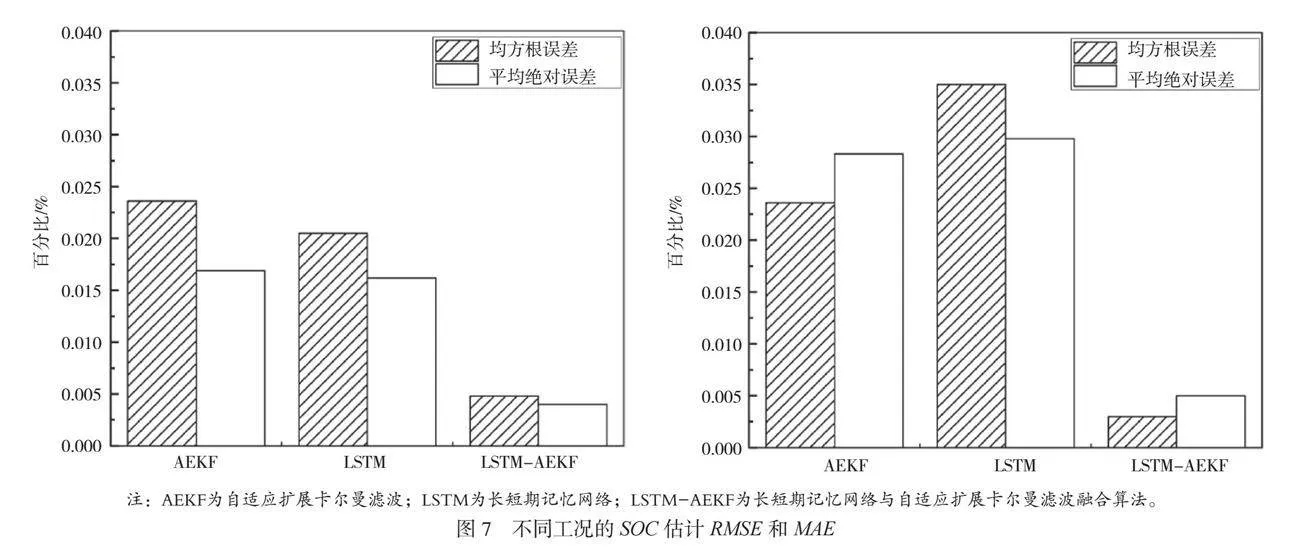
不同工况的SOC估计均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）如图7所示，从图7可以看出，使用LSTM-AEKF算法后，SOC的估计精度提高了。RMSElt;0.5%，MAE为0.48%，低于AEKF算法和LSTM算法的RMSE和MAE。 试验结果表明，在25 ℃锂电池的不同工况下，使用LSTM-AEKF算法估计SOC降低了试验误差，估计性能良好。LSTM-AEKF算法在DST、FUDS工况的RMSE分别为0.48%、0.22%，比AEKF算法低2.15%，比LSTM算法低1.5%，提高了SOC的估计精度，说明基于二阶RC等效电路模型的LSTM-AEKF算法易于推广，效果良好。

4 结论

电池的荷电状态估计是保障电池供电系统安全可靠运行的一项不可缺少的步骤。本文研究了不同电池工况的SOC估计，开发了以LSTM作为基准，结合AEKF提高其SOC估计性能的LSTM-AEKF算法。本文在二阶RC等效电路模型的基础上在线辨识电池参数，在线参数辨识可以提升SOC估计的准确性。研究结果表明，AEKF或LSTM算法估计SOC或或LSTM算法估计SOC的结果误差偏大，RMSE和MAE分别可达3.3%和3.15%。本文将这2种方法改进融合进行SOC估计，RMSE和MAE分别大幅降至0.22%和0.40%。与传统的AKEF算法和LSTM算法相比，本文提出的算法提升了SOC的估计精度，能够满足实际生产中对锂电池SOC的估计精度需求。

参考文献

[1]杨文荣，朱赛飞，陈阳，等.基于改进安时积分法估计锂离子电池组SOC[J].电源技术，2018，42（2）：183-184.

[2]刘迪，李琳，姜晓健.基于安时积分法和UKF的锂电池SOC估测[J].新型工业化，2021，11（11）： 125-128.

[3]杨帆，和嘉睿，陆鸣，等.基于BP-UKF算法的锂离子电池SOC估计[J].储能科学与技术，2023，12（2）：552-559.

[4]徐艳民.基于BP-EKF算法的电池SOC估计[J].汽车技术，2018（2）： 19-23.

[5]刘兴涛，李坤，武骥，等.基于EKF-SVM 算法的动力电池SOC 估计[J].汽车工程，2020，42（11）： 1522-1528.

[6]李堂，黄康，毛行奎，等.基于EKF算法的动力锂离子电池SOC估计[J].电器与能效管理技术，2023（9）：62-68.

[7]来鑫，李云飞，郑岳久，等.基于SOC-OCV优化曲线与EKF的锂离子电池荷电状态全局估计[J].汽车工程，2021，43（1）： 19-26.

[8]张武，孙士山，张家福.基于自适应无迹卡尔曼滤波的动力电池SOC估计[J].电源技术，2021，45（1）：14-17.

[9]张远进，吴华伟，叶从进.基于AUKF-BP神经网络的锂电池SOC估算[J].储能科学与技术，2021，10（1）：237-241.

[10]吴小慧，张兴敢.锂电池二阶RC等效电路模型参数辨识[J].南京大学学报（自然科学版），2020，56（5）：754-761.

[11]刘征宇，黎盼春，朱诚诚，等.基于组合模型的锂电池参数辨识和电池荷电状态在线联合估计[J].中国机械工程，2020，31（10）：1162-1168.

[12]陈息坤，孙冬.锂离子电池建模及其参数辨识方法研究[J].中国电机工程学报，2016，36（22）： 6254-6261.