装配式建筑套筒灌浆饱满度和密实度检测方法研究

摘 要：目前装配式建筑的技术难点是利用套筒灌浆连接构件。因此本文针对套筒灌浆密实度进行无损检测，基于阻尼振动的方法，提出了一种基于密实度指数的灌浆质量评价方法。在阻尼振动检测方法中，振动波形通过套筒灌浆会出现衰减，不同介质的衰减程度不同，由此可以检测灌浆质量问题。由于所在区间的不同，因此密实度指数可以准确地评价套筒灌浆的密实度，若大于0.5，则表现均匀密实。在测试试验中，本文采用14点位综合测量的方法，对5个工程的灌浆套筒进行检测，证实了本文所提出的检测方法和评价方法的有效性。

关键词：装配式建筑；套筒；灌浆；饱满度；密实度

中图分类号：TU 75" 文献标志码：A

在城镇化建设的过程中，民用住宅需求持续增加，这为建筑行业提供了一个非常好的发展契机。在这样的情况下，各种新的技术开始涌现，更具实用性和稳定性的方法逐渐成熟，并获得广泛应用[1]。在民用住宅施工的过程中，装配式建筑结构已经成为一种很常用的方式。这种方法不仅施工质量好，而且施工效率也比较高，可以在保证质量的前提下加快施工进度。在装配式建筑施工的过程中，套筒灌浆技术是影响建筑质量的最重要因素之一[2]。在装配式建筑的构件连接处，一般以套筒为连接件，内部为钢筋，在套筒和钢筋之间灌入高强度砂浆，从而对构件间进行连接。在这种处理方式下，装配式建筑连接处的强度取决于套筒和高强度砂浆之间的连接强度、高强度砂浆和钢筋之间的连接强度[3]。由此可见，如果套筒内高强度砂浆灌注饱满并且密实，就可以获得更好的连接强度，从而保障装配式建筑整体的安全性。因此，在这种情况下，对套筒灌浆后的饱满度和密实度进行检测，就成为判定灌浆质量是否达标的重要依据。本文主要采用不破坏建筑外观的无损检测方法进行研究工作。

1 基于阻尼振动的无损检测方法

在装配式建筑的构件连接过程中，套筒灌浆后，内部质量形成一个隐蔽的工程。因为套筒为金属、灌浆为非金属、钢筋为金属，所以灌浆后就形成了多层的金属和非金属交错的一种结构形态。而从实际施工经验来看，套筒内砂浆的厚度并不大，受内部钢筋所占体积制约，砂浆层厚度仅为5mm～6mm。

比较薄的砂浆层一旦出现灌注不均的情况，就会大大降低套筒连接的强度，导致极大的安全隐患。如果采用钻孔法进行灌浆质量检测，就会破坏建筑结构。因此，建立套筒灌浆质量无损检测方法势在必行。

本文采用基于阻尼振动的方法对灌浆饱满度和密实度进行检测，以明确套筒内的灌浆质量优劣。振动波形产生后，在介质传播过程中，会逐渐衰减和削弱。但是，不同介质对振动波形的衰减能力是不同的。如果灌浆足够饱满和密实，那么振动波形主要受到砂浆介质的衰减作用影响。如果灌浆不够饱满和密实，就会有空气夹杂于其中，振动波形会同时受到砂浆和空气或者是只受到空气介质的衰减影响。

阻尼振动是指振动波形在介质传输的过程中，会受到介质所带来的阻尼效应而逐渐衰减。在衰减的过程中，振动波形的幅度会逐渐变小。介质给振动波形施加的摩擦阻力的计算过程如公式（1）所示。

fr=-γv " " " " " " " " " " " " " " " "（1）

式中：fr为振动波形在介质中传播时受到的摩擦阻力；γ为介质施加给振动波形的阻力系数；v为振动波形在某一种介质中传播的速度。

根据牛顿第二定律，可以将振动波形传递的过程描述为一个二阶常值系数方程，计算过程如公式（2）所示。

（2）

式中：x为振动波形的幅度，也称位移参量；t为振动波形传递的时间；β为介质的阻尼系数，因介质不同而不同；ω0为振动波形的固有角频率。

阻尼系数的计算方法如公式（3）所示。

（3）

式中：β为介质的阻尼系数；γ为介质施加给振动波形的阻力系数；m为介质质量。

固有角频率的计算方法如公式（4）所示。

（4）

式中：ω0为振动波形的固有角频率；k为介质给振动波形提供的弹性模量；m为介质质量。

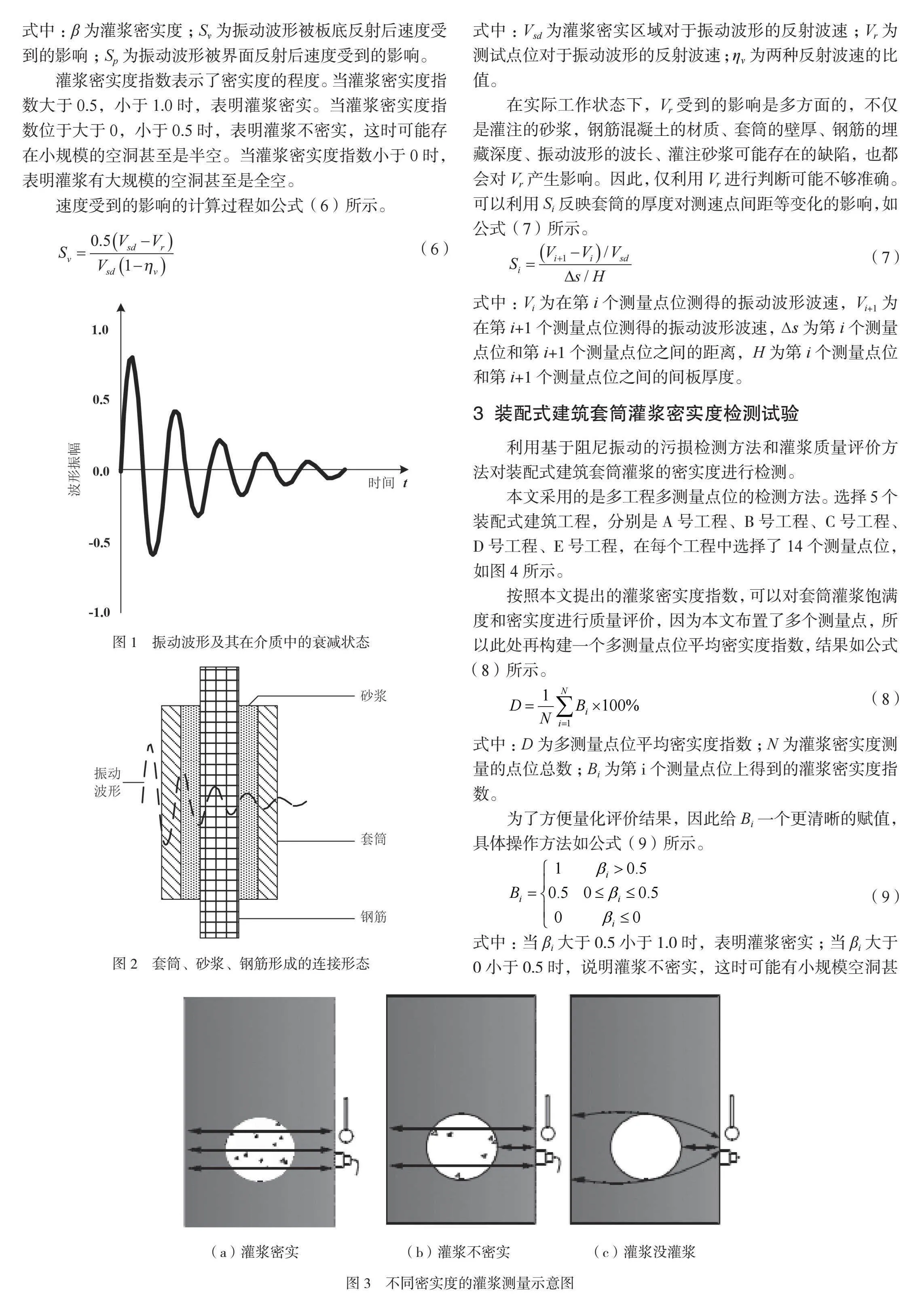
振动波形及其在介质中的衰减状态，如图1所示。

套筒、砂浆、钢筋形成连接形态后，如图2所示。

图2中，振动波形通过套筒灌浆连接件后，就会逐步衰减，通过这个衰减程度就可以判断内部砂浆的介质均匀性。

2 灌浆饱满度和密实度的质量评价

利用阻尼振动法对套筒灌浆质量进行检测，要根据特定的评价参数来判断灌浆质量。这时，可能会出现灌浆密实、不密实和没有灌浆等情况，如图3所示。

对套筒内灌浆的饱满度和密实度来说，领域内有最具针对性的密实度指数，其数学表达如公式（5）所示。

β=1-Sv-Sp " " " " " " " " " " " " " " " （5）

式中：β为灌浆密实度；Sv为振动波形被板底反射后速度受到的影响；Sp为振动波形被界面反射后速度受到的影响。

灌浆密实度指数表示了密实度的程度。当灌浆密实度指数大于0.5，小于1.0时，表明灌浆密实。当灌浆密实度指数位于大于0，小于0.5时，表明灌浆不密实，这时可能存在小规模的空洞甚至是半空。当灌浆密实度指数小于0时，表明灌浆有大规模的空洞甚至是全空。

速度受到的影响的计算过程如公式（6）所示。

（6）

式中：Vsd为灌浆密实区域对于振动波形的反射波速；Vr为测试点位对于振动波形的反射波速；ηv为两种反射波速的比值。

在实际工作状态下，Vr受到的影响是多方面的，不仅是灌注的砂浆，钢筋混凝土的材质、套筒的壁厚、钢筋的埋藏深度、振动波形的波长、灌注砂浆可能存在的缺陷，也都会对Vr产生影响。因此，仅利用Vr进行判断可能不够准确。可以利用Si反映套筒的厚度对测速点间距等变化的影响，如公式（7）所示。

（7）

式中：Vi为在第i个测量点位测得的振动波形波速，Vi+1为在第i+1个测量点位测得的振动波形波速，∆s为第i个测量点位和第i+1个测量点位之间的距离，H为第i个测量点位和第i+1个测量点位之间的间板厚度。

3 装配式建筑套筒灌浆密实度检测试验

利用基于阻尼振动的污损检测方法和灌浆质量评价方法对装配式建筑套筒灌浆的密实度进行检测。

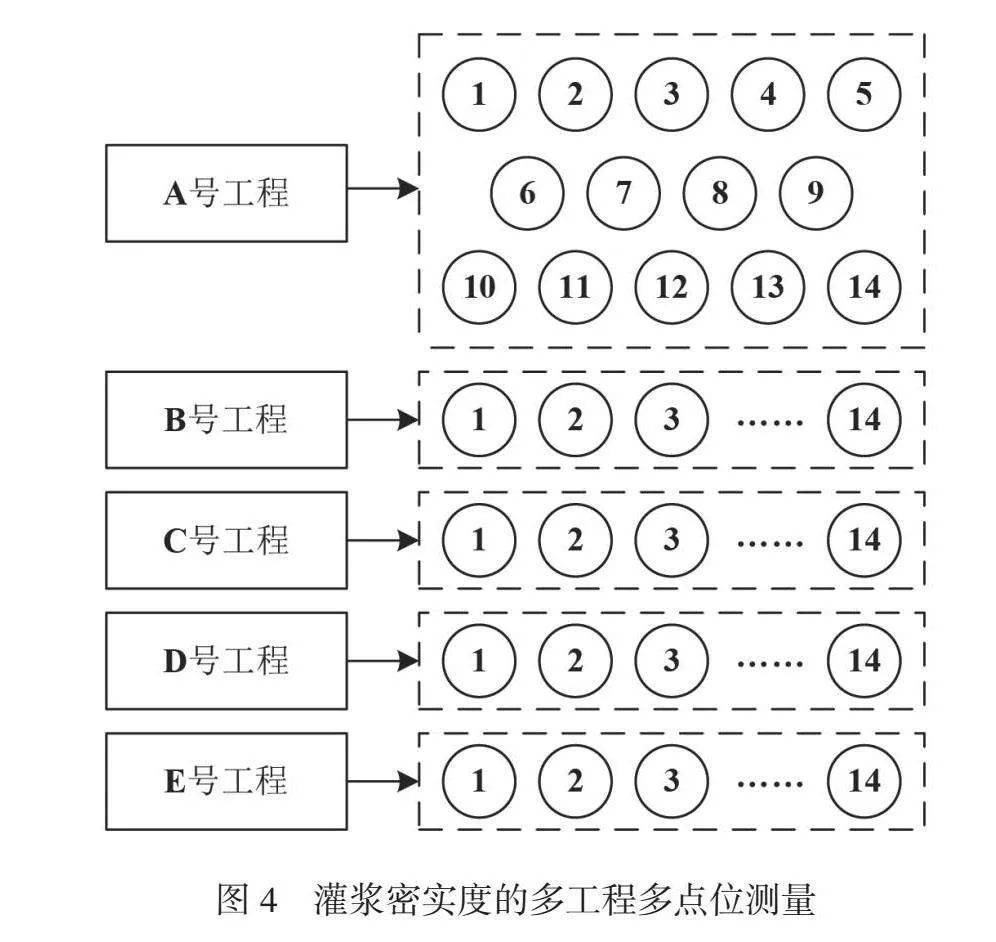
本文采用的是多工程多测量点位的检测方法。选择5个装配式建筑工程，分别是A号工程、B号工程、C号工程、D号工程、E号工程，在每个工程中选择了14个测量点位，如图4所示。

按照本文提出的灌浆密实度指数，可以对套筒灌浆饱满度和密实度进行质量评价，因为本文布置了多个测量点，所以此处再构建一个多测量点位平均密实度指数，结果如公式（8）所示。

（8）

式中：D为多测量点位平均密实度指数；N为灌浆密实度测量的点位总数；Bi为第i个测量点位上得到的灌浆密实度指数。

为了方便量化评价结果，因此给Bi一个更清晰的赋值，具体操作方法如公式（9）所示。

（9）

式中：当βi大于0.5小于1.0时，表明灌浆密实；当βi大于0小于0.5时，说明灌浆不密实，这时可能有小规模空洞甚至是半空情况；当βi小于0时，说明灌浆有大规模的空洞甚至是全空。

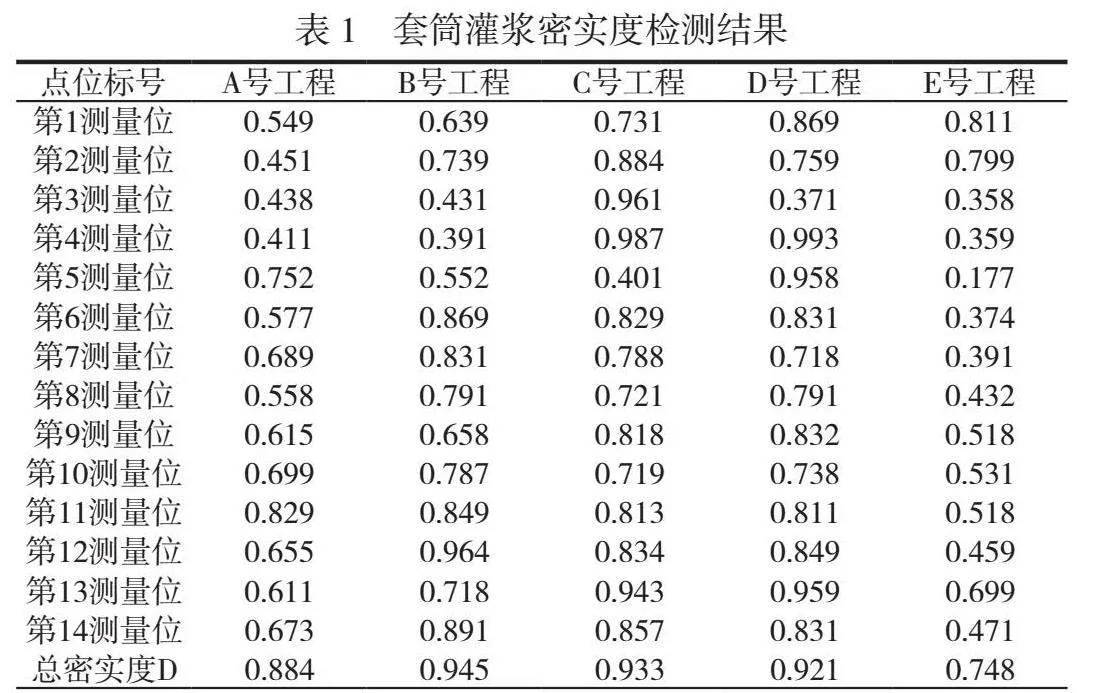
按照上述方法，对图4中5个工程的套筒灌浆密实度进行检测，得到的结果见表1。

在表1中，第一列表示14个测量点位和各点位汇总后的总密实度，第二列为A号工程、第三列标为B号工程、第四列为C号工程、第五列为D号工程、第六列为E号工程。

5个工程的多点位测量汇总结果，如图5所示。

从汇总结果可以看出，B号工程14个点位的套筒的灌浆密实度最好，为0.945。其次是C号工程14个点位的套筒灌浆密实度，为0.933。排在第三位的是D号工程14个点位的套筒密实度，为0.921。第四位的是A号工程14个点位的套筒灌浆密实度，为0.884。灌浆密实度最差的是E号工程14个点位的套筒密实度，为0.748。根据这一组测量结果可以看出：本次灌浆的总体质量很好，只有E号工程应该采取进一步的处理措施以提高其密实度质量。

4 结论

装配式建筑已经成为我国城市民用建筑的重要形式，该建筑极大地提高了城市建设的施工质量和施工效率。在装配式建筑的实践过程中，完成装配件连接是最关键的工艺。套筒连接是最常见的装配式连接方式。因为套筒为金属、灌浆为非金属、钢筋为金属，所以灌浆后就形成了多层金属和非金属交错的一种结构形态。为了检验套筒连接后内部灌浆的密实度，本文构建了阻尼振动模型。利用这种模型可以准确分析套筒内灌浆的密实程度。结果表明，对不同位置的套筒连接进行密实度检验，阻尼振动模型都能有效地检测密实度。

参考文献

[1] 陈旭东，汪秀娟，刘志豪，等. 无损检测技术在套筒灌浆密实度检测中的应用研究[J]. 兰州工业学院学报，2017，24（1）：49-53.

[2] 李宁波，钱稼茹，叶列平，等. 竖向钢筋套筒挤压连接的预制钢筋混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报，2016，37（1）： 31-40.

[3] 李丽红，耿博慧，齐宝库，等. 装配式建筑工程与现浇建筑工程成本对比与实证研究[J]. 建筑经济，2022，35（9）：102-105.