新型定转子齿混合励磁双凸极电机转矩特性研究

摘 要：为增大混合励磁双凸极电机的电磁转矩并减少转矩脉动，本文分析混合励磁双凸极电机电磁转矩产生机理。为有效利用磁阻转矩，对电机的定、转子齿分别进行开槽设计，使电机自感曲线分布发生变化，有效削弱负向磁阻转矩，减少磁阻转矩，增大平均转矩。对通场路耦合进行仿真验证，结果表明定转子开槽可在不增加转矩脉动的情况下提升转矩输出能力。

关键词：双凸极电机；混合励磁；转矩脉动；定转子开槽

中图分类号：TM 351" " " " " " " " 文献标志码：A

混合励磁双凸极电机（下文简称 HEDS 电机）是由双凸极永磁电机发展而来的，在双凸极永磁电机的基础上增加了励磁绕组和导磁桥。其不仅具有永磁型双凸极电机结构简单、效率高等优点，而且磁通调节能力很强。HEDS电机与其他双凸极电机类似，转矩波动明显，在一定程度限制了其应用范围。为进一步增大电机输出转矩，减少转矩波动，在电机控制方面，戴卫力等[1]分析了提前角度控制能提高转矩的内在机理，试验得到转速与最佳提前角度值的关系表，增大电机输出转矩。刘星等[2]为增大电机输出转矩，抑制转矩脉动，在三相三状态控制的基础上提出三相六状态控制策略。在电机本体方面，孙强等[3]利用斜槽减少电机转矩脉动，提出规定的双凸极电机有1个使转矩脉动率最小的最佳转子斜槽角。本文提出一种优化定转子极面结构的方法，在定转子中同时进行开槽，使HEDS电机相电感发生变化，削弱由磁阻转矩产生的负转矩，达到增大电机在高速状态下转矩的效果。进行场路耦合仿真，对比优化前后输出转矩与转矩脉动，验证了本文方法的合理性和正确性。

1 电机结构与数学模型

1.1 电机结构

1台三相12/8 HEDS电机模型如图1所示，定转子为双凸极结构，定子由铁心、永磁体、励磁绕组和ABC三相电枢绕组组成。图中定子轭部分为永磁体，其共有12个齿，在定子槽中分别放置A相、B相、C相绕组和W励磁绕组。转子为8个齿，结构简单，为叠压铁心。在运行过程中转子不断旋转振动，因此将转子设计为纯铁芯结构。与有永磁体和线圈的永磁电机或异步电机相比，次结构可以提高电机的可靠性，也有利于电机转子散热。在永磁体与励磁绕组之间安放导磁桥，磁导大小与磁路通过的面积成正比，励磁绕组通电后，产生的磁场会经过导磁桥，因此导磁桥宽度直接影响励磁绕组调节磁场能力[4]。为留出放置励磁绕组的空间位置，定子齿采用三相平行齿。

1.2 数学模型

HEDS电机数学模型包括电压方程、磁链方程以及转矩方程等，该数学模型描述了HEDS电机主要物理量之间的关系，可作为HEDS电机理论研究的基础。忽略相绕组间互感，HEDS电机电压方程、磁链方程和转矩方程如公式（1）所示。

（1）

式中：up、ip、rp和ψp分别为相电压、相电流、相电阻和磁链；p=A，B，C；ψpr 、ψpw和ψpm分别为相磁链、励磁磁链和永磁磁链；Tp、Tr、Tpw和Tpm分别为总电磁转矩、磁阻转矩、励磁转矩和永磁转矩；iw、Lp、Lpw和θ为励磁电流、自感、相绕组与励磁绕组间互感和转子位置角。本文主要讨论iw=0，Tpw=ipiw=0，因此下文中未考虑励磁转矩Tpw。

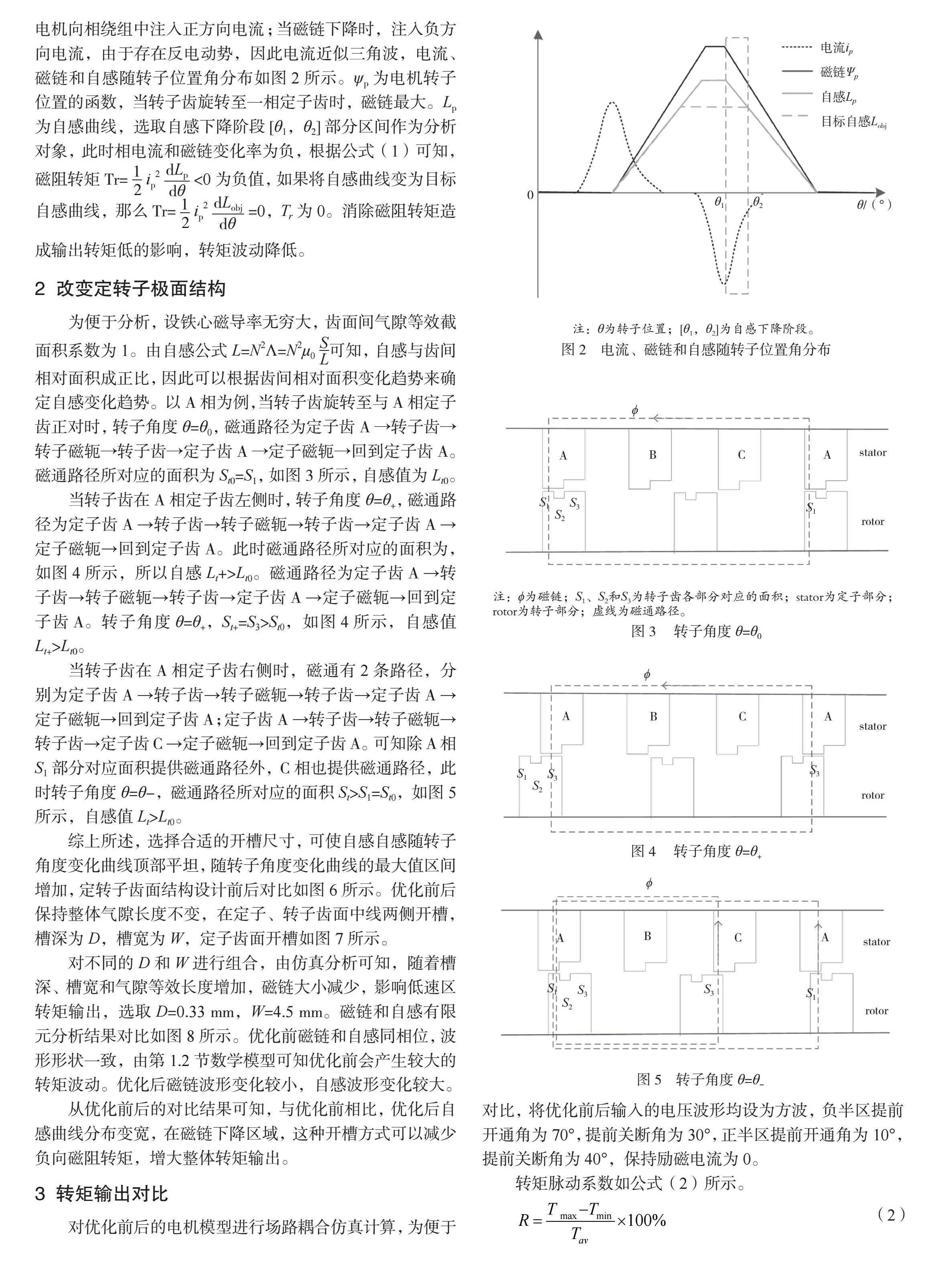
当高速运行且磁链增加时，为获得转矩，常规HEDS电机向相绕组中注入正方向电流；当磁链下降时，注入负方向电流，由于存在反电动势，因此电流近似三角波，电流、磁链和自感随转子位置角分布如图2所示。ψp为电机转子位置的函数，当转子齿旋转至一相定子齿时，磁链最大。Lp为自感曲线，选取自感下降阶段[θ1，θ2]部分区间作为分析对象，此时相电流和磁链变化率为负，根据公式（1）可知，磁阻转矩Tr=ip2lt;0为负值，如果将自感曲线变为目标自感曲线，那么Tr=ip2=0，Tr为0。消除磁阻转矩造成输出转矩低的影响，转矩波动降低。

2 改变定转子极面结构

为便于分析，设铁心磁导率无穷大，齿面间气隙等效截面积系数为1。由自感公式L=N2Ʌ=N2μ0可知，自感与齿间相对面积成正比，因此可以根据齿间相对面积变化趋势来确定自感变化趋势。以A相为例，当转子齿旋转至与A相定子齿正对时，转子角度 θ=θ0，磁通路径为定子齿A→转子齿→转子磁轭→转子齿→定子齿A→定子磁轭→回到定子齿A。磁通路径所对应的面积为St0=S1，如图3所示，自感值为Lt0。

当转子齿在A相定子齿左侧时，转子角度θ=θ+，磁通路径为定子齿A→转子齿→转子磁轭→转子齿→定子齿A→定子磁轭→回到定子齿A。此时磁通路径所对应的面积为，如图4所示，所以自感Lt+gt;Lt0。磁通路径为定子齿A→转子齿→转子磁轭→转子齿→定子齿A→定子磁轭→回到定子齿A。转子角度θ=θ+，St+=S3gt;St0，如图4所示，自感值Lt+gt;Lt0。

当转子齿在A相定子齿右侧时，磁通有2条路径，分别为定子齿A→转子齿→转子磁轭→转子齿→定子齿A→定子磁轭→回到定子齿A；定子齿A→转子齿→转子磁轭→转子齿→定子齿C→定子磁轭→回到定子齿A。可知除A相S1部分对应面积提供磁通路径外，C相也提供磁通路径，此时转子角度 θ=θ-，磁通路径所对应的面积Stgt;S1=St0，如图5所示，自感值Ltgt;Lt0。

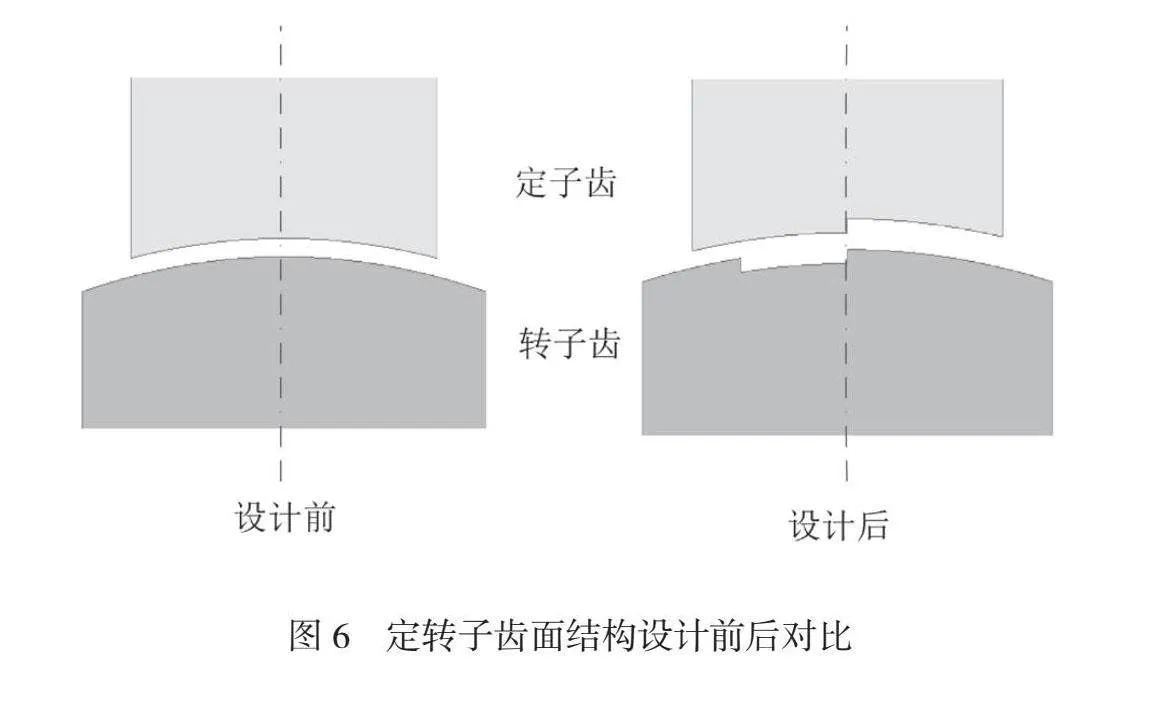
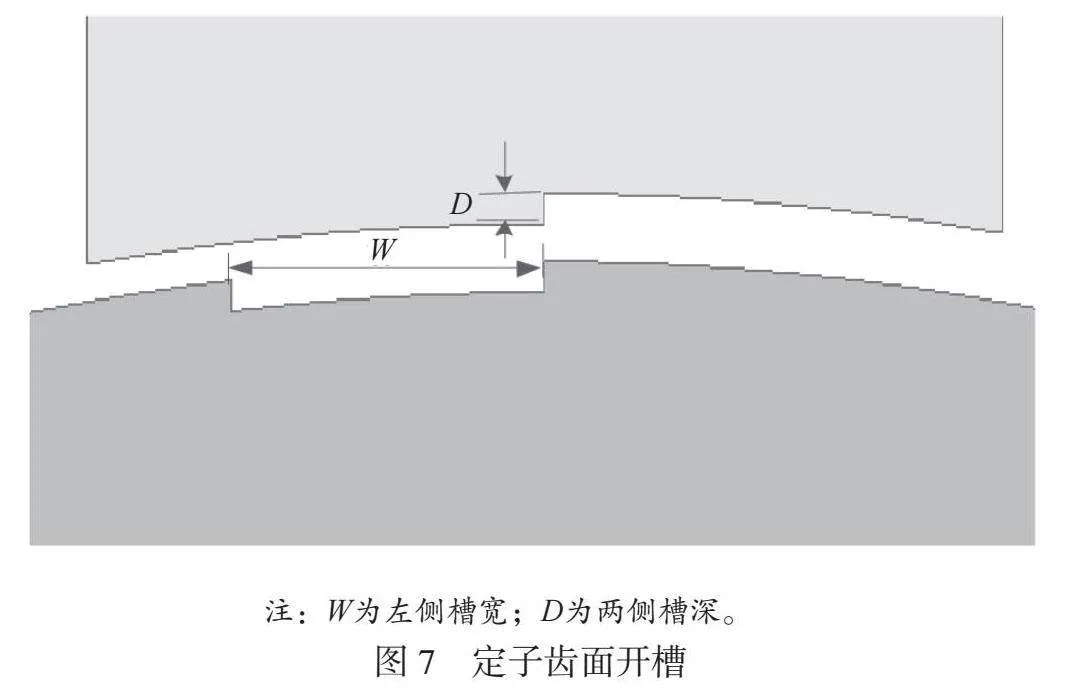
综上所述，选择合适的开槽尺寸，可使自感自感随转子角度变化曲线顶部平坦，随转子角度变化曲线的最大值区间增加，定转子齿面结构设计前后对比如图6所示。优化前后保持整体气隙长度不变，在定子、转子齿面中线两侧开槽，槽深为D，槽宽为W，定子齿面开槽如图7所示。

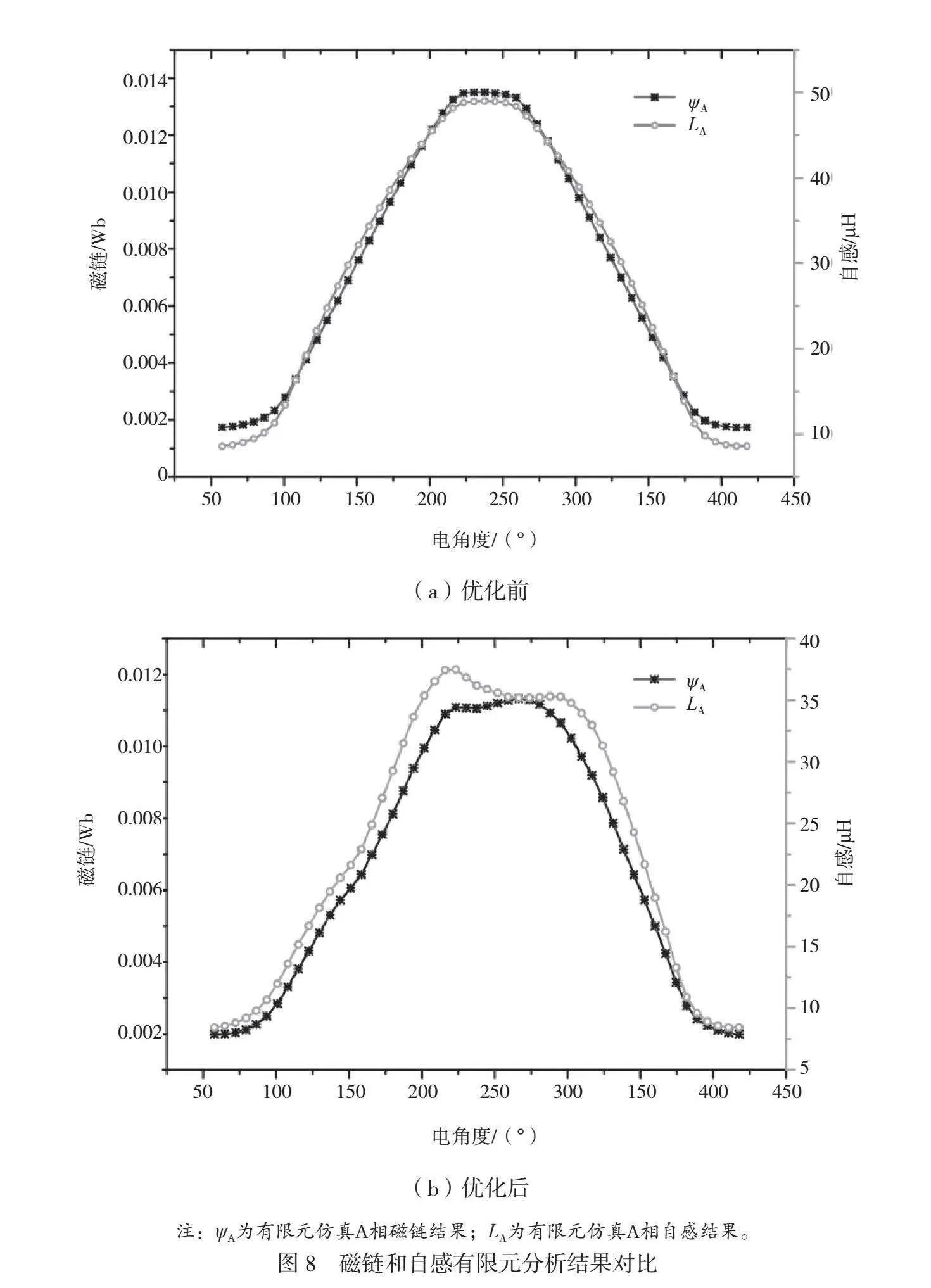
对不同的D和W进行组合，由仿真分析可知，随着槽深、槽宽和气隙等效长度增加，磁链大小减少，影响低速区转矩输出，选取D=0.33 mm，W=4.5 mm。磁链和自感有限元分析结果对比如图8所示。优化前磁链和自感同相位，波形形状一致，由第1.2节数学模型可知优化前会产生较大的转矩波动。优化后磁链波形变化较小，自感波形变化较大。

从优化前后的对比结果可知，与优化前相比，优化后自感曲线分布变宽，在磁链下降区域，这种开槽方式可以减少负向磁阻转矩，增大整体转矩输出。

3 转矩输出对比

对优化前后的电机模型进行场路耦合仿真计算，为便于对比，将优化前后输入的电压波形均设为方波，负半区提前开通角为70°，提前关断角为30°，正半区提前开通角为10°，提前关断角为40°，保持励磁电流为0。

转矩脉动系数如公式（2）所示。

（2）

式中：Tmax为当电机稳态运行时最大转矩值；Tmin为当电机稳态运行时最小转矩值；Tav为当电机稳定运行时平均转矩值。

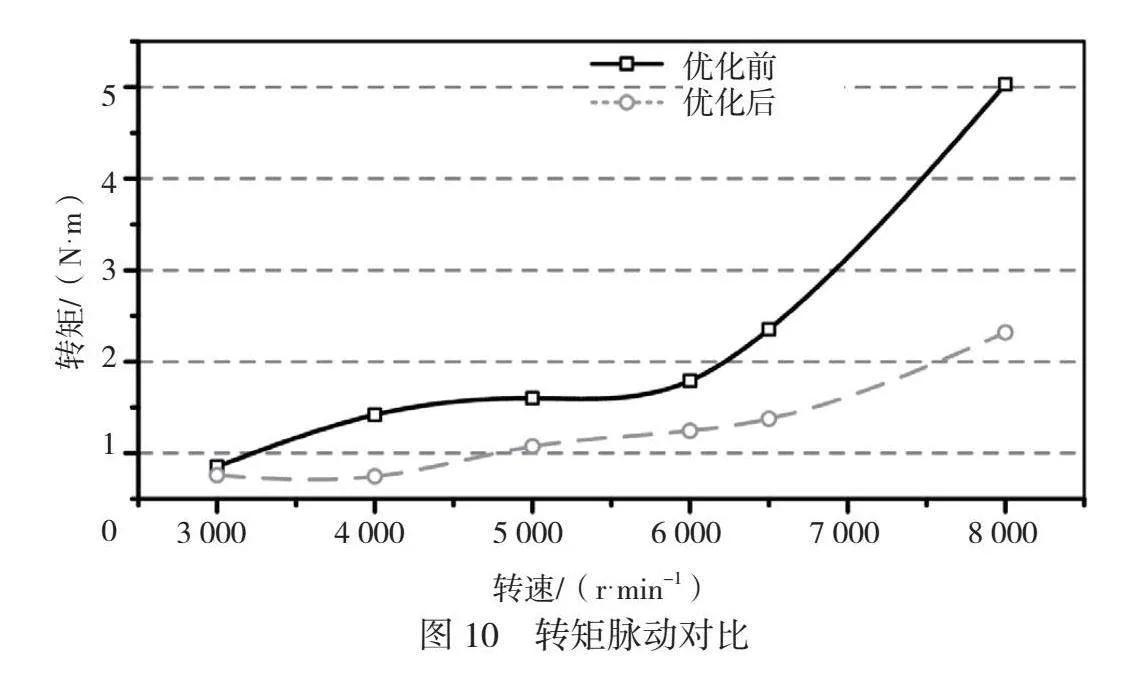
输出转矩对比如图9所示，转矩脉动对比如图10所示。根据仿真结果可以得到以下2个结论。1）优化后的电机模型转矩和转矩脉动系数在较大的电机转速范围内均得到了有效改进，转矩增大，转矩脉动减少。2）转速越快，改进效果越明显，当转速n=8 000 r/min时，转矩提高1倍，转矩脉动系数降低53.8%。

4 结论

本文设计的新型的定转子齿面结构不仅能有效减少转矩脉动系数，而且增加了输出转矩，使HEDS电机转矩输出能力得到全面提升。转速越高，效果越明显，当转速n=8 000 r/min时，转矩提高100%，转矩脉动系数降低53.8%。

参考文献

[1]戴卫力，王慧贞，严仰光.电励磁双凸极电机的提前角度控制[J].电机工程学报，2007，27（27）：88-93.

[2]刘星，陈志辉，朱杰，等.电励磁双凸极电动机三相六拍控制策略研究[J].中国电机工程学报，2013，33（12）：138-144.

[3]孙强，程明，周鹗，等.双凸极永磁电动机转矩脉动分析[J].电工技术学报，2002，17（5）：10-15.

[4]朱孝勇，程明，花为，等.新型混合励磁双凸极永磁电机磁场调节特性分析及试验研究[J].中国电机工程学报，2008，266（3）：90-95.