地铁车轮失圆原因分析及镟修策略分析

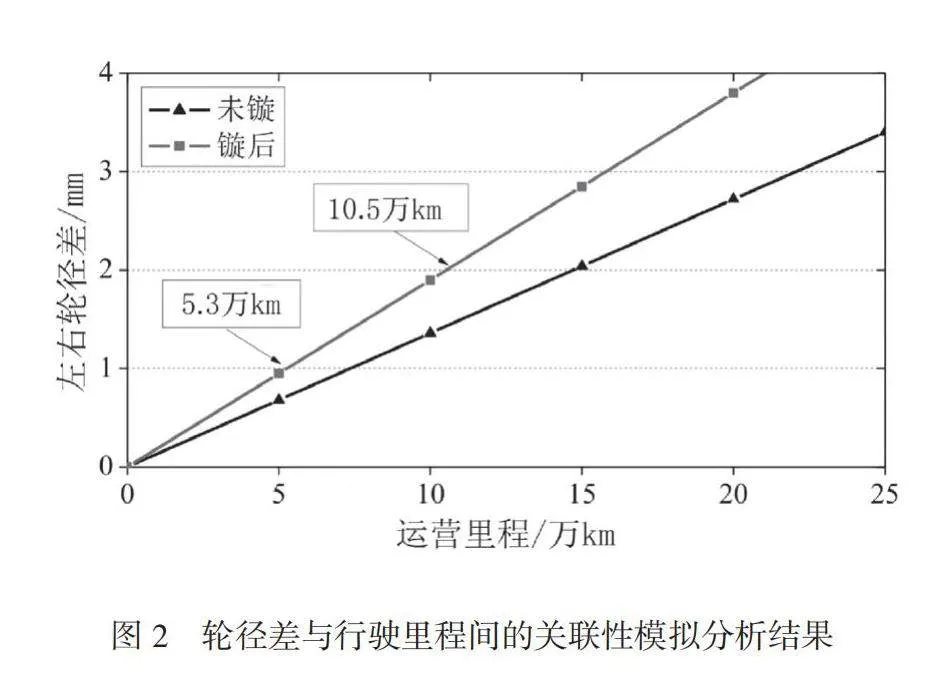
摘要：为提升整个地铁运行质量与效率，本文分析了地铁车轮失圆原因分析和镟修策略。通过实践调查与模拟分析的方式论述地铁车轮失圆主要原因，并通过车辆系统动力学模型、结合动力学性能评价提出相应车轮失圆镟修策略。结果表明，P2共振是车轮5～8边形主要成因，采取的镟修策略如下：在同轴轮径差为1mm条件下，车辆行驶5.3万km时控制车辆调头；在同轴轮差为2mm条件下，车辆行驶10.5万km时对车辆进行检查，针对具体情况合理选择29.5mm、30mm、31mm或31.5mm的轮缘厚度进行镟修处理。本文通过上述策略为地铁车辆安全、稳定运行提供支持，对保障地铁车辆安全、稳定运行具有重要的价值。

关键词：地铁；车轮；失圆；镟修

中图分类号：U231""""""""" 文献标志码：A

地铁是现代城市交通的重要组成部分，直接关系到城市居民的生活与社会发展。然而大量实践研究表明，在地铁运行过程中，地铁车轮很容易出现各种问题，失圆是较常见的一种，会影响地铁车辆的安全、稳定运行。因此，相关部门应对地铁车轮失圆问题予以高度重视，针对失圆问题的主要原因制定出科学、合理的镟修策略方案，以加强车轮失圆问题防治。基于此，本文研究了地铁车轮失圆原因分析和镟修策略，对进一步提升地铁车辆运行的安全性与稳定性具有重要意义。

1地铁车轮失圆原因分析

1.1车轮不圆度通过频率

为了准确了解地铁车轮失圆的主要原因，本文分析了车轮不圆度通过频率。所研究地铁列车为ATO模式，车辆运行速度为0km/h～75km/h，其中，速度在60km/h以上的时间段较多，占整个车辆行驶时间的66.4%左右。车轮的半径为420mm，5～8阶多边形的波长（λ）处于0.33mm～0.53mm。由此可以计算出该车轮的不圆度通过频率f，如公式（1）所示。

f=v（1）

式中：v为最高速与速度为60km/h的差值。

由计算可知，f为30Hz～63Hz。以此为基础，找出与f相差较小的车轮固有频率，从而确定车轮失圆的主要原因。

1.2轮对模态分析

为了了解车轮的固有频率特点，本文采用模态分析方式，对地铁动车与拖车轮对进行模拟分析，以此确定不同模态条件下车轮的固有频率。观察轮对实际情况可发现，拖车轮对结构比动车轮对更复杂，多出1个轮齿与齿轮箱。构建车辆模型时，通过刚性连接方式，将轮对与轴向连接到一起，忽略其他模块间的相互作用。构建车辆模型后，在轮对轴向方面，将网格划分模式设置成“8节点6面体”；在齿轮与齿轮箱方面，将网格划分模式设置成“4节点4面体”，并将整个模型设置成自由边界，并通过ANSYS软件对车辆模型进行模拟分析[1]。结果显示，在一阶模态条件下，动车轮对的扭转频率为74.7Hz，拖车轮对的扭转频率为80.4Hz，动车轮对弯曲共振频率为84.3Hz，拖车轮对弯曲共振频率为81.6Hz。以此为基础，与上述计算出来的f值进行比较，可以发现模态分析结果与f值存在较大差异，表明地铁车辆运行时，在弯曲工作作用下，基本不会出现车轮失圆问题。

1.3轨道振动测试

现代地下铁路领域共有5种轨道形式，分别为普通扣件轨道（A类型），竖直静态刚度为40kN/mm左右；双层非线性减振扣件轨道（B类型），竖直静态刚度为8～14kN/mm；中量级钢弹簧浮置板轨道（C类型）；重量级钢弹簧浮置板轨道（D类型）；减振垫浮置板轨道（E类型）。其中，E类型轨道较稀少，在轨道中的比例只有2.5%左右，因此可省略该类型轨道[2]。进一步观察4种常见类型轨道，可以发现，轨道运行时表面出现的波磨非常小，基本可以忽略不计。将轨道轨枕上部与跨中区域作为测点，对轨道进行敲击试验，确定出不同类型轨道的频响函数。鉴于篇幅有限，在此省略模拟分析结果（下同）。由模拟分析可知，对于A类型钢轨，测点在跨中钢轨区域，处于一阶条件下时，共振频率约为204Hz。说明轨道使用过程中，钢轨、轨枕与轨道板的振动形式基本一致。从竖直pinned-pinned共振频率角度来看，试验结果约为1100Hz，这种情况下，轨枕处的振动波长与2个轨枕间距基本相同，节点在轨枕区域。其他3种类型轨道的频响函数基本一致，但共振频率存在一定差异。由此表明，在轨道结构方面，共振频率与轮对的f值差异较大，因而出现车轮失圆问题的概率并不高。

1.4车辆振动测试

以上述4种类型轨道为例，对列车在不同轨道条件下行驶时的轴箱竖直振动加速度进行时频分析与频谱分析。进行时频分析时，振动加速度频率为0Hz～800Hz，列车行驶速度为60km/h～75km/h。由分析结果可知，轨道形式的不同对加速度的频率基本无明显影响，结果数值相差不大，主要为50Hz～80Hz。由频谱分析结果可知，采用A类型轨道时，车辆的振动加速度频率约为64Hz；采用B类型轨道时，加速度频率约为53Hz；采用C类型轨道时，加速度频率为58Hz～66Hz；采用D类型轨道时，加速度频率则为66Hz。由此可以发现，不论采用哪种类型轨道，车辆振动频率与f值的差异均不大，表明车辆共振是导致地铁车轮失圆的主要原因。

2地铁车轮失圆的镟修策略

2.1车辆系统动力学模型构建

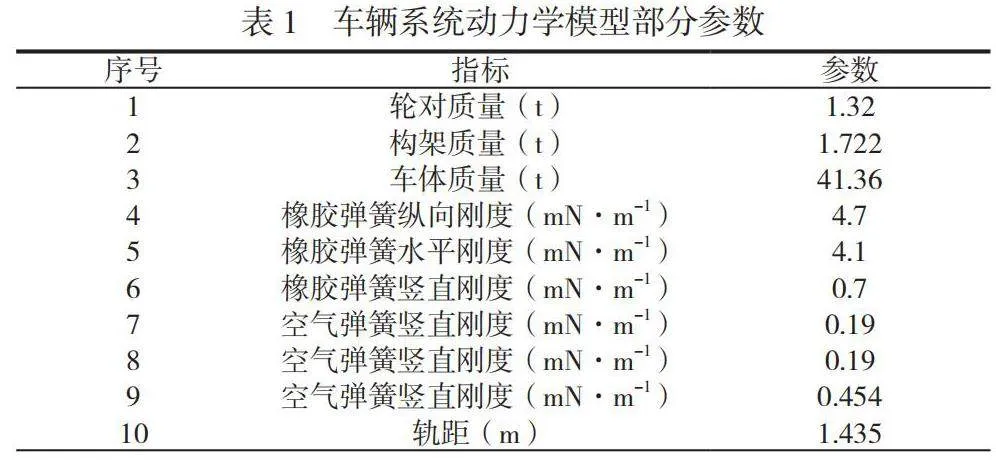
为了设计出最佳镟修策略，应对地铁车系统的动力学特点进行模拟分析。模拟分析过程中，本文以SIMPACK软件为主要工具，构建出地铁车辆的有限元模型。构建模型时，先对车辆进行简化，去除车辆中座椅、电气设备等对车辆动力学特性影响较小的部件，将整个车辆简化成含有1个车体、2个构架和4个轮对的模型。构建转向架模型时，选择“H”形焊接结构，其中一系为叠层橡胶弹簧，二系为大挠度高柔性空气弹簧。同时，结构中还包括减振器等部件。进而本文以一系弹簧为媒介，将轮对与转向架固定到一起，以二系空气弹簧为媒介，将车体与构件固定到一起。此外，为了降低研究难度，还应考虑下述3个方面：将整个车辆均看成钢体结构；忽略车辆行驶中产生的弹性变形；忽略其他因素对轮轨接触的影响，将二者看成非线性接触等[3]。并以此为基础，在SIMPACK软件中分别设置相应参数，其中部分主要参数见表1，使软件自动构建出车辆系统的动力学模型，如图1所示。

2.2动力学性能评价分析

2.2.1评价指标选择

进行轨道车辆动力学性能评价时，一般选择2个指标，具体如下所示。

第一，平稳性。平稳性用于评价车辆行驶质量，车辆稳定性越好，车辆行驶质量越高，内部人员舒适性越好。对车辆平稳性进行评价的主要公式[4]如公式（2）所示。

式中：a为车轮的振动加速度；f为振动的频率；F（f）为修正系数，可通过人类对振动频率的敏感性与相关资料查询获得。

计算出车辆的平稳性后，通过查询Sperling评价等级，确定车辆的平稳性等级。其中，车辆W值在2.5以下、机车W值在2.75以下为1级，表明车辆平稳性优秀；车辆W值在2.5～2.75、机车W值在2.75～3. 10为2级，表明车辆稳定性良好；车辆W值在2.75～3.0、机车W值在3.10～3.45为3级，表明车辆稳定性合格。

第二，安全性。安全性用于评价地铁车辆行驶过程中是否出现安全事故，是评价地铁车辆动力学性能的重要指标之一。目前，进行地铁车辆安全性评价时主要考虑2个方面：一是脱轨系数，主要通过水平力与竖向力的比值来计算，记作Q/P，根据计算结果，将脱轨系数划分成2个等级，分别为合格（≤0.9）与良好（≤0.8）；二是轮重减载率，即在水平力非常小的工况下，由一侧车轮减载导致车辆脱轨的概率计算如公式（3）所示[5]。

（3）

式中：ΔP为轮对的减载量；P为两侧轮对竖向力的均值；P2与P1均为某一侧轮对的竖向力。

根据计算结果，将减载率划分成2个等级，分别为合格（≤0.62）与良好（≤0.60）。

2.2.2车辆动力学性能评价结果

以图2所示模型为基础，分别模拟分析车辆动力学性能水平。由模拟分析结果可知，在平稳性方面，行驶里程为20万km范围内时，车辆平稳性为1.7左右，属于Sperling评价等级中的1级，即车辆平稳性优秀。与此同时，通过对车辆进行实际检测能够发现，车辆平稳性为1.5～2. 1，虽然存在较大波动，但整体与模拟分析结果相差并不大，均处于Sperling评价等级中的1级范围内，表明模拟分析结果是准确的，可作为车辆平稳性的分析结果。在脱轨系数方面，行驶里程为20万km范围内时，随着车辆行驶里程数不断提升，车辆脱轨系数基本无明显改变，均处于0.15～0.43，远低于0.8，表明车辆安全性良好，在安全限值范围内。在减载率方面，行驶里程为20万km范围内时，随着车辆里程数不断提升，减载率也基本无明显变化，在0.19～0.22小幅变化，表明车辆安全性良好，在安全限值范围内。

2.3镟修策略制定

根据上述分析结果可知，地铁车辆行驶20万km范围内时，车辆动力学特性基本保持良好，因此以20万km为一个周期，定期对地铁车辆进行镟修处理，即可使车辆安全、平稳运行。

2.3.1车辆调头与车轮镟修周期确定

由实践工作经验可知，由于车辆未调头行驶，因此会导致车辆车轮出现磨损，使车轮失圆，从而影响车辆的正常运行。为了提升车辆运行效果，则应注重车辆调头与车轮镟修周期的制定。通过对镟修处理前、后车辆行驶状况进行整理与分析，可得如图2所示的结果。由图2可知，车轮镟修前、后，随着车辆里程数增加，两侧轮径差呈逐渐上升的趋势，相对于镟修前，镟修后的轮径差上升幅度更显著。行驶里程达到5.3万km时，轮径差超过1.0mm，应控制车辆调头行驶。当车辆行驶里程达到10.5万km时，轮径差超过2.0mm，超过车辆安全行驶规定要求，因此需要对车轮进行镟修处理。但需要注意的是，由于车轮所处位置与转动速度并不相同，使车轮的磨耗水平存在一定差异，因此在实际中应以2个月为周期，定期对车轮磨耗水平进行检查，以及时发现车轮失圆问题，提升车辆运行的安全性与平稳性。

2.3.2轮对镟修模版自动匹配

由相关资料可知，我国地铁车辆车轮共有9种薄轮缘踏面外形，其中常见的有4种，分别为LM-29.5、LM-30、LM-31和LM-31.5，因此本文研究中仅将这4种的车轮作为镟修模版，对轮对镟修模版自动匹配进行分析。为了快速选择最佳的镟修模版，本文设计了一种地铁轮对镟修模版自动匹配程序。该程序先对轮对踏面外形进行检测，进行初步处理后，将其作为镟修模版匹配的主要参数。再将这些参数录入匹配程序，即可针对轮对具体情况选择最佳镟修模版，在保证两侧轮径差在0.5mm范围内的同时，控制镟修切削量，提升车轮的使用黏性，降低车辆运维成本。

3应用分析

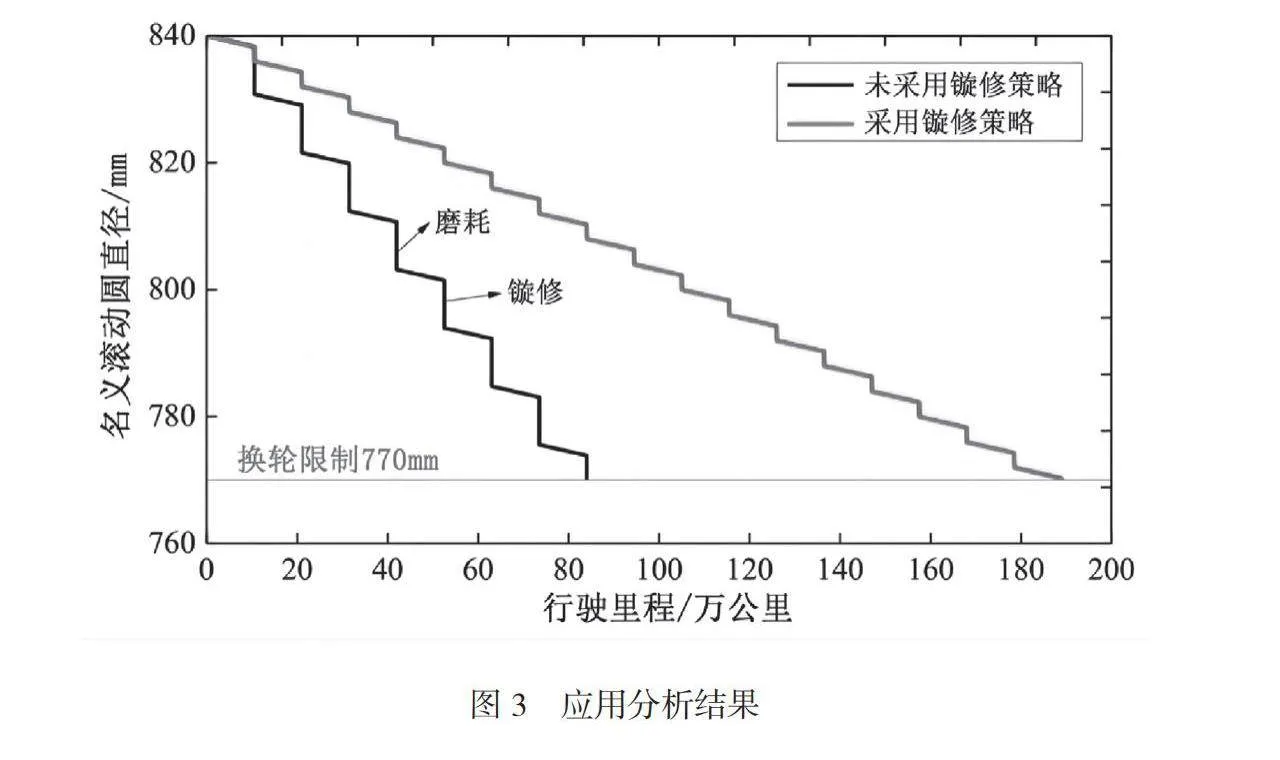
以某地铁为例，根据上述镟修策略处理地铁车轮失圆问题，以验证上述镟修策略是否合理。通过应用分析可以得到如图3所示的结果。由图3可知，未采用上述镟修策略前，车辆行驶80万km左右时即可达到使用寿命限值；采用上述镟修策略后，车辆行驶190万km左右时才达到使用寿命限值，远高于未采用镟修策略前。表明上述镟修策略是合理的，有利于提升地铁车辆行驶安全性、稳定性与寿命，对地铁系统的运行具有重要意义。

4结语

综上所述，分析了地铁车轮失圆原因，并介绍了一种车轮失圆问题的镟修策略，通过该镟修策略的应用，可以在投入较低成本的同时，有效解决车轮失圆问题，显著提升车轮的行驶里程数，为整个地铁系统安全、稳定的运行提供支持。

参考文献

[1]梁红琴，姜进南，陶功权，等. 基于轴箱垂向振动加速度的地铁车轮失圆状态诊断方法[J]. 中南大学学报（自然科学版），2024，55（01）：431-443.

[2]邓磊鑫，谢清林，陶功权，等. 基于轴箱振动与动力学模型驱动的高速列车车轮失圆状态识别方法[J]. 机械工程学报，2023，59（3）：110-121.

[3]黄江伟，方配丰，田聚峰，等.120km/h地铁B型车车轮失圆特征分析[J]. 电力机车与城轨车辆，2022，45（3）：70-75.

[4]沈钢，王兴远，毛鑫，等. 城市轨道交通车辆车轮失圆的机理研究及仿真分析[J]. 城市轨道交通研究，2021，24（7）：79-83.

[5]黄贵发，廖云，李修文，等. 融合振动位移滤波及加速度多阶谱的车轮失圆诊断方法[J]. 质量与可靠性，2021，35（3）：27-35.