基于R语言的主成分分析与聚类分析在成绩评价中的应用

摘 要：主成分分析与聚类分析是当前大数据时代较有应用前景的数据分析方法。首先介绍主成分分析与聚类分析的原理以及在R语言中的算法实现。利用主成分分析，建立一种可以综合评价成绩的方式，通过成绩综合评价的得分进行相应的排名，然后根据主成分中的得分进行聚类分析。通过对20名学生考试成绩的分析与评价，得出的结果可以用来反映学生的学习情况与教师的教学成效，为成绩的管理提供一种合理且便于操作的方式。

关键词：主成分分析 聚类分析 K-means聚类 R语言 成绩分析

中图分类号：G642

Application of Principal Component Analysis and Cluster Analysis Based on R Language in Score Evaluation

SHEN Dandan

Changzhi Medical College， Changzhi， Shanxi Province， 046000 China

Abstract： Principal Component Analysis and Cluster Analysis are the most promising data analysis methods in the current era of big data. Firstly， it introduces the principles of Principal Component Analysis and Cluster Analysis， as well as their algorithm implementation in R language. Using Principal Component Analysis， it establishes a comprehensive score evaluation method， and ranks based on the comprehensive score evaluation， and then conducts Cluster Analysis based on the scores in the principal components. By analyzing and evaluating the exam scores of 20 students， the results can be used to reflect the learning situation of students and the teaching effectiveness of teachers， providing a reasonable and easy to operate way for score management.

Key Words： Principal Component Analysis; Cluster Analysis; K-means cluster; R language; Score analysis

当前信息化时代背景下，面对高校教学中学生成绩错综复杂的情形，利用传统的成绩评定方式有一定的局限性，通常是采用加权评分法或对所有成绩求和，然后依据绝对分数来进行等级评定。然而在设置加权的权重时，人为主观因素较大，直接对所有成绩求和无法反映学生真实的学习情况与能力，利用绝对分数来进行成绩评定时很大程度上依赖于考试的形式、试卷的结构以及难易程度等，这些方法都存在一定的缺陷，不利于客观、科学地评价学生的学习情况，也不利于真实地反映教师的教学成果。主成分分析是把所有变量之间相关联的复杂关系进行简化分析，聚类分析能从大量的数据中对有意义的数据分布模式进行挖掘，将主成分分析与聚类分析应用于学生成绩评价时，可以弥补传统成绩评定方法所带来的缺陷，更能科学客观地反映学生的学习情况，从而为教学管理提供一定指导[3]。

1 主成分分析

1.1 ; 主成分分析基本思想

通常研究人员所要处理的问题大多是关于多变量的问题，变量越多，反应问题的信息更全面，但也无疑给问题增加了难度，从而研究人员希望在保证不丢失大量原始信息量的基础上，通过少量变量来反映问题。主成分分析就是采用降维的方式将具有一定相关性的多变量化为少数几个不相关的综合变量的统计分析方法。

主成分分析的基本原理：将原始具有相关性的变量通过线性组合的方式形成新的线性无关的变量。第一个线性组合即为第一个新变量，要求它在所有线性组合中方差最大，含有的信息量最多。如果第一个线性组合无法提取原始变量的所有信息，则考虑第二个线性组合即第二个新变量，且第一个新变量中所含有的信息不出现在第二个新变量中，即这两个变量的协方差为零。继续进行这个过程，直到包含的信息与原始变量包含的信息量相差不大。此过程即为主成分分析降维的过程，经过此过程可以使问题得到简化[8]。

1.2 主成分分析基本理论

设所研究的问题包含个变量，可构成向量，协方差阵为，对做线性组合：

得到新的综合变量，这里表示与之间的相关系数，所做的线性组合要求满足以下条件：

（1）；（2） 与（）互不相关；（3） 是与不相关的所有线性组合中方差最大的。若满足以上条件，则即为主成分，分别称为原始变量的第1、第2、第个主成分，且对应方差依次递减，通常选择前几个方差较大且所含信息总和达到以上的主成分。

每个主成分所含信息量的大小用方差来刻画，要使的方差达到最大，即使达到最大，而协方差阵的特征值就是对应主成分的方差，特征值所对应的特征向量就是。是第个主成分的方差贡献率，表示第个主成分提取个变量的信息量，该值越大，表示对应主成分所含信息量越多，为主成分的累计方差贡献率，表示前个主成分所含原始变量的信息量。

1.3 利用主成分分析对成绩评价的步骤

设个学生，成绩有个变量，第个学生的第项成绩为，则个学生个变量可构成原始数据矩阵为。

（1）对原始数据进行标准化，，其中，，。

（2）标准化数据后，计算相关系数矩阵，，其中。

（3）计算的特征值与相应的特征向量，因而可以得到个主成分。

（4）计算各个主成分的方差贡献率与累计方差贡献率，当前个主成分累计贡献率达到80%以上，确定主成分的个数为。

（5）写出综合评价函数：，函数值即为学生综合得分。

2 聚类分析

2.1 聚类分析基本思想

聚类分析是基于数据的相似性，根据数据的特征进行分类，聚合为一类的数据之间有较高的相似度，而类间的数据相似度较小。于是给定一组数据后，可以先确定度量数据之间相似程度的统计量，以此统计量为依据对数据进行划分，把相似度较大的数据归为一类，把另外的一些相似度较大的数据又归为另一类，相似度大的归到一个小的分类单位，相似度小的归到一个大的分类单位，直至所有的数据都归类完毕，把所有数据划分后，就会形成一个由小到大的分类系统[2]。

K-means聚类算法

K-means聚类算法，属于划分聚类算法中的典型算法，是一种快速聚类法，相对其他算法具有操作简便快捷的特点。K-means法中，首先要把全部数据分成k个类，把相似度高的数据划分为一类，这样就能得到类内相似度高，类间相似度低的几簇数据。通过计算类中数据的平均值来确定相似度。K-means算法流程图如图1。

3 主成分分析与聚类分析在学生成绩综合分析中的应用

3.1 研究的基础数据

本文中研究的基础数据来源于长治医学院2023—2024学年第一学期某专业班级20名学生的5门课程期末成绩，分别表示变量思想道德与法治、基础化学、大学英语A、医用物理学、医用高等数学。如表1所示。

3.2 设计实现与实验结果

使用R语言进行主成分分析得到结果，如图2所示。

由图2中的分析结果，在输出的5个主成分中，前3个主成分的累计贡献率已达89%，所以可用前3个主成分来进行分析。loading表示载荷，其值是 的系数，也是特征值对应的特征向量，由标准化变量所表达的主成分的关系式为：

由此得到综合评价函数为

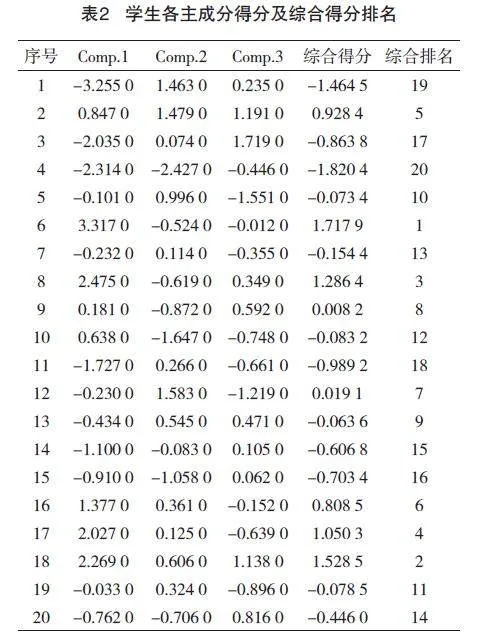
将成绩数据代入得到表2中的3个主成分得分、综合得分与排名，该结果是由统计分析得出，此过程很大程度上不受主观因素的影响，因此用在实例分析上较合理客观。

结果分析：由主成分分析得出的综合排名与原始成绩均值的排名相差不大，有极少数差异较大。例如序号为10号的同学，他的总分排名是6，而综合排名是12，该同学在第一主成分得分较高，说明数学、物理、化学成绩较好，在第二、三主成分得分较低，说明该生的思想道德与法治、大学英语成绩并不好。序号为12号的同学，总分排名是12，而综合排名是7，该生在第二主成分得分较高，第一、三主成分得分为负值。根据以上表中数据，能够对学生在各课程上的学习情况有较客观的了解与掌握，根据得分情况与综合得分了解他们成绩的特点，从而帮助分析学生的薄弱与优势科目，进而提升教师的教学成效。

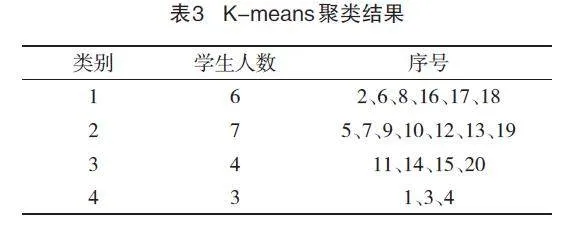
针对学生成绩数据，依据前3个主成分得分，利用R语言进行K-means聚类分析，得到的结果如表3所示。

从表3可看出：将学生分为四类，第一类学生各科成绩较理想，学习上较积极主动。第二类学生成绩中等，有些同学成绩或高或低，有偏科现象，在学习上积极主动性需要加强。第三类学生的第一主成分得分较低，数理化成绩较不理想，要注重学习兴趣的培养。第四类学生在各科成绩上均不理想，之后要更多注重基础知识的学习。

通过以上对主成分分析与聚类分析的思想、原理的阐述，以及对实验结果的分析，可以看出，通过主成分分析与聚类分析来对学生成绩划分评定时，较传统划分方式更科学、合理，能更好地反映出学生的学习情况与教师教学成效。

4 结语

主成分分析与聚类分析作为当前最有应用前景的数据分析方法，已被广泛应用于社会生活的各个领域。运用R语言通过主成分分析与聚类分析来划分学生的成绩，方便易行，且所得结果也具有合理性、有效性，这为教师开展教学工作与实践提供有效的参考与指导，不断提升教学质量。

对学生而言，学生可以认识到自身成绩的类别，认清自己各科成绩的差异，从而更有针对性地找到深入的方向，持续深造，提升自我。对教师而言，更清晰地了解学生的成绩类别，结合学生的平时表现、学习背景进一步了解学生，从而因材施教，增强学生学习积极性与主动性。

个变量，可构成向量，协方差阵为，对做线性组合：，这里表示与之间的相关系数，所做的线性组合要求满足以下条件：；（2） 与（是与不相关的所有线性组合中方差最大的。若满足以上条件，则即为主成分，分别称为原始变量的第1、第2、第个主成分，且对应方差依次递减，通常选择前几个方差较大且所含信息总和达到的方差达到最大，即使达到最大，而协方差阵的特征值就是对应主成分的方差，特征值所对应的特征向量就是。是第个主成分的方差贡献率，表示第个主成分提取个变量的信息量，该值越大，表示对应主成分所含信息量越多，为主成分的累计方差贡献率，表示前个主成分所含原始变量的信息量。个学生，成绩有个变量，第个学生的第项成绩为，则个学生个变量可构成原始数据矩阵为。，其中，，。，，其中。的特征值与相应的特征向量，因而可以得到个主成分。与累计方差贡献率，当前个主成分累计贡献率达到80%以上，确定主成分的个数为。，函数值即为学生综合得分。 （1）为所有数据与相应聚类中心的均方差之和；为数据对象中的一个数据；为类的均值。这个公式的聚类标准是要使每个聚类能具备以下条件：各类能尽量自行密集，而类间尽量分散。K-means算法流程图如图1。参考文献

[1]龙钧宇.基于均值聚类和决策树算法的学生成绩分析[J].计算机与现代化，2014（6）：79-83．

[2]叶福兰.基于K-means均值算法的学生成绩分析：以福州外语外贸学院信息管理与信息系统专业为例[J].贵阳学院学报（自然科学版），2017，12（3）：17-20.

[3]展金梅，陈君涛，田飞.数据挖掘技术在高校学生成绩分析中的应用[J].科技资讯，2023，21 （19）： 202-205.

[4]李凤英，许洪光，周方，等.基于数据挖掘和K-Means算法的高校学情数据集成研究[J].黑龙江工程学院学报，2022，36（4）：31-36.

[5]金玉.基于学习大数据的学生学习成绩预测关键技术研究[D].南京：东南大学，2021.

[6]钱玲，饶江泉，罗小泉，等.基于成绩分析探讨知识背景对学习的影响[J].科技资讯，2023， 21 （9）： 234-237.

[7]郭继东，郑可晗，张晶，等.基于主成分分析的学习效果因素调查分析研究[J].机电工程技术，2022，51（5）：165-169.

[8]郭兰兰，付政庆，衣秋杰.主成分分析法在学生成绩分析与评价中的应用[J].高教学刊，2021（3）：88-91.