基于RBF神经网络的建筑暖通水温节能控制设计

摘 要：本文基于RBF神经网络提出一种超低能耗建筑暖通空调冷水温度优化控制方法。在该方法中，对建筑暖通空调水系统的运行工况进行辨识。通过辨识结果，建立建筑暖通空调冷水温度优化控制器，利用RBF 神经网络对控制器进行在线优化，获取房间预测温度输出。利用预测信息和设定的目标函数，不断在线修正预测温度输出，得到最佳暖通空调冷水温度，对空调冷水温度进行优化控制。试验结果表明，该方法能够有效地对建筑暖通水温进行节能控制，具有较高的控制精度和可靠性。

关键词：RBF神经网络；建筑暖通；水温节能控制

中图分类号：TU 83" " 文献标志码：A

随着人们对能源消耗和环境保护的日益关注，建筑节能成为一个重要的研究领域[1]。建筑暖通系统是建筑能耗的重要组成部分，其中水温控制是影响能耗和舒适性的关键因素之一。传统的建筑暖通水温控制方法往往存在能耗高、控制精度低等问题。张帆等[3]采用蚁群算法来增强其全局搜索能力。叶立等[2]则引入粒子群优化算法来对控制器参数进行优化。本文以此为基础，基于RBF神经网络进行建筑暖通水温节能控制设计。

1 建筑暖通水温节能优化控制方法

1.1 建筑暖通空调水系统运行工况分析

在神经网络中，使用公式（1）来描述神经元的计算过程。

xi=∑（ωi×xi-1）+θ " "（1）

式中：xi为第i个神经元的输入；ωi为神经元之间的连接强度；xi-1为第i-1个神经元的输出；θ为阈值。

计算神经元的激活函数如公式（2）所示。

（2）

式中：f（）为激活函数；exp（）为指数函数。

神经元的输入是由前一层神经元的输出和连接强度加权求和得到的，再加上阈值，通过激活函数对输入进行非线性转换，得到神经元的输出。

计算隐含层的输出如公式（3）所示。

bf=f ∑（（ωij×bf-1）+θj ） （3）

计算输出层的输出如公式（4）所示。

cf=f ∑（（υij×bf-1）+γj） （4）

式中：bj为隐含层的输出；cf为输出层的输出；ωij为神经元i和j之间的连接强度；υij为神经元i和j之间的权值系数；θj为神经元的连接强度阈值；γj为神经元i的阈值；f（）为激活函数。

计算输出层的一般化误差如公式（5）所示。

ekj=Ct-tk " "（5）

式中：ekj为输出层的一般化误差；Ct为输出层的输出；tk为目标值。

计算误差函数的极小值如公式（6）所示。

ykt=∑（ekj2）" （6）

式中：ykt为误差函数的极小值；ekj为输出层的一般化误差。

计算输出层的误差，并根据误差函数的极小值来评估神经网络的性能。输出层的一般化误差是输出层输出与目标值之间的差异，即网络的预测误差。误差函数的极小值是对所有输出层神经元的一般化误差进行求和。在训练过程中，通过调整神经网络的参数和权重来最小化误差函数的极小值，从而提高网络的预测准确性。常用的方法是使用梯度下降算法来更新参数和权重，以逐步减小误差函数的极小值[4-5]。

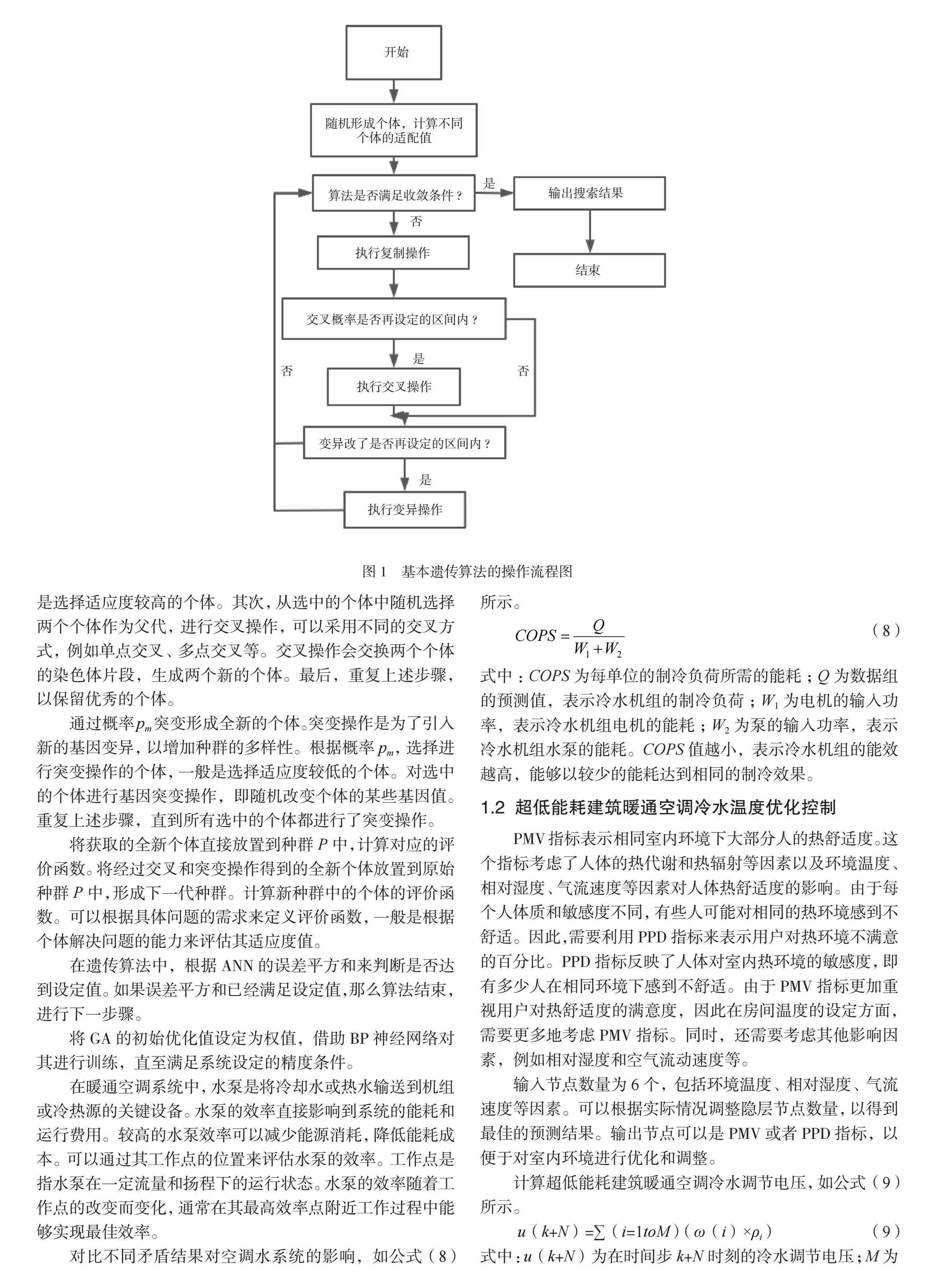
图1为遗传算法的流程图，第一步是将种群进行初始化处理。在实际编码的过程中，通常使用实数进行编码，以便更灵活地表示网络的结构和权值。

在遗传算法的每一代中，需要计算不同个体的适应度，适应度函数通常为评估个体解决问题能力的指标。具体适应度函数的选择取决于具体的问题和目标。根据适应度函数的计算结果，可以对种群中的个体进行排序，以便选择适应度较高的个体作为下一代的父代，从而保留优秀的个体解。

在遗传算法中，根据个体的适应度值和概率，可以选择不同的网络个体作为下一代的父代。具体的选择如公式（7）所示。

（7）

式中：pi为个体i被选中的概率，fi为个体i的适应度值。通过将个体的适应度值归一化，可以得到每个个体被选中的概率。

根据这些概率值，可以使用轮盘赌选择（Roulette Wheel Selection）的方法。该方法的基本思想是根据个体被选中的概率，在轮盘上选择父代个体。

计算累积概率：qi=∑pi，即第i个个体被选中的累积概率。生成一个随机数r，使0≤r≤1。

根据随机数r，选择第一个满足qi-1≤r≤qi的个体作为父代。

通过这样的选择过程，可以根据个体的适应度值选择适应度较高的个体作为下一代的父代，进一步进行遗传操作，从而优化网络的结构和权值。

首先，根据概率pc，选择进行交叉操作的个体，通常是选择适应度较高的个体。其次，从选中的个体中随机选择两个个体作为父代，进行交叉操作，可以采用不同的交叉方式，例如单点交叉、多点交叉等。交叉操作会交换两个个体的染色体片段，生成两个新的个体。最后，重复上述步骤，以保留优秀的个体。

通过概率pm突变形成全新的个体。突变操作是为了引入新的基因变异，以增加种群的多样性。根据概率pm，选择进行突变操作的个体，一般是选择适应度较低的个体。对选中的个体进行基因突变操作，即随机改变个体的某些基因值。重复上述步骤，直到所有选中的个体都进行了突变操作。

将获取的全新个体直接放置到种群P中，计算对应的评价函数。将经过交叉和突变操作得到的全新个体放置到原始种群P中，形成下一代种群。计算新种群中的个体的评价函数。可以根据具体问题的需求来定义评价函数，一般是根据个体解决问题的能力来评估其适应度值。

在遗传算法中，根据ANN的误差平方和来判断是否达到设定值。如果误差平方和已经满足设定值，那么算法结束，进行下一步骤。

将GA的初始优化值设定为权值，借助BP神经网络对其进行训练，直至满足系统设定的精度条件。

在暖通空调系统中，水泵是将冷却水或热水输送到机组或冷热源的关键设备。水泵的效率直接影响到系统的能耗和运行费用。较高的水泵效率可以减少能源消耗，降低能耗成本。可以通过其工作点的位置来评估水泵的效率。工作点是指水泵在一定流量和扬程下的运行状态。水泵的效率随着工作点的改变而变化，通常在其最高效率点附近工作过程中能够实现最佳效率。

对比不同矛盾结果对空调水系统的影响，如公式（8）所示。

（8）

式中：COPS为每单位的制冷负荷所需的能耗；Q为数据组的预测值，表示冷水机组的制冷负荷；W1为电机的输入功率，表示冷水机组电机的能耗；W2为泵的输入功率，表示冷水机组水泵的能耗。COPS值越小，表示冷水机组的能效越高，能够以较少的能耗达到相同的制冷效果。

1.2 超低能耗建筑暖通空调冷水温度优化控制

PMV指标表示相同室内环境下大部分人的热舒适度。这个指标考虑了人体的热代谢和热辐射等因素以及环境温度、相对湿度、气流速度等因素对人体热舒适度的影响。由于每个人体质和敏感度不同，有些人可能对相同的热环境感到不舒适。因此，需要利用PPD指标来表示用户对热环境不满意的百分比。PPD指标反映了人体对室内热环境的敏感度，即有多少人在相同环境下感到不舒适。由于PMV指标更加重视用户对热舒适度的满意度，因此在房间温度的设定方面，需要更多地考虑PMV指标。同时，还需要考虑其他影响因素，例如相对湿度和空气流动速度等。

输入节点数量为6个，包括环境温度、相对湿度、气流速度等因素。可以根据实际情况调整隐层节点数量，以得到最佳的预测结果。输出节点可以是PMV或者PPD指标，以便于对室内环境进行优化和调整。

计算超低能耗建筑暖通空调冷水调节电压，如公式（9）所示。

u（k+N）=∑（i=1toM）（ω（i）×ρi） （9）

式中：u（k+N）为在时间步k+N时刻的冷水调节电压；M为模糊神经网络的输出节点数量；ω（i）为每个节点的权重；ρi为空调调节阀电压取值。

在模糊神经网络中，通过网络的训练过程得到权重 ω（i），可以根据具体的算法和数据进行计算和调整。这些权重可以对输入变量与输出变量之间的关系进行建模和表示。通过调整权重，模糊神经网络可以学习并预测未来的冷水调节电压。

计算设定控制目标函数j如公式（10）所示。

j=∑（i=ltoN）（ω1×|y（k+i）-λ（k+i）|ω2×yr（k+i）） " （10）

式中：N为预测时间步数；ω1和ω2是权重系数；|y（k+i）-λ（k+i）|为测试房间的期望温度与实际温度之间的差值；yr（k+i）为房间最高温度和最低温度的差值。

控制目标函数的主要作用是优化控制策略，使测试房间的期望温度与实际温度之间的差值最小，并且将房间的温度控制在最高温度和最低温度的差值范围内。通过调整权重系数，可以根据实际需求来平衡不同的目标。

采用优化方法对性能进行优化，可以使用RBF（径向基函数）模糊神经网络来获取未来控制时长内暖通空调系统中冷冻水泵的调节电压，如公式（11）所示。

ρj，N（k+1）=∑（i=1tom）（ω（i）×Φ（||[aj，N（k+1），cj，N（k+1）]-[μi，σi]||）） （11）

式中：ρj，N（k+1）为经过调整和修正后的控制参数；aj，N（k+1）、cj，N（k+1）为经过调整和修正后的控制参数；ω（i）为每个节点的权重；Φ（）为径向基函数；[μi，σi]为径向基函数的中心和标准差。RBF模糊神经网络的训练过程通常包括确定径向基函数的中心和标准差以及节点的权重。通过训练过程，模糊神经网络可以学习并预测未来控制时长内的冷冻水泵调节电压，以优化性能。

2 仿真研究

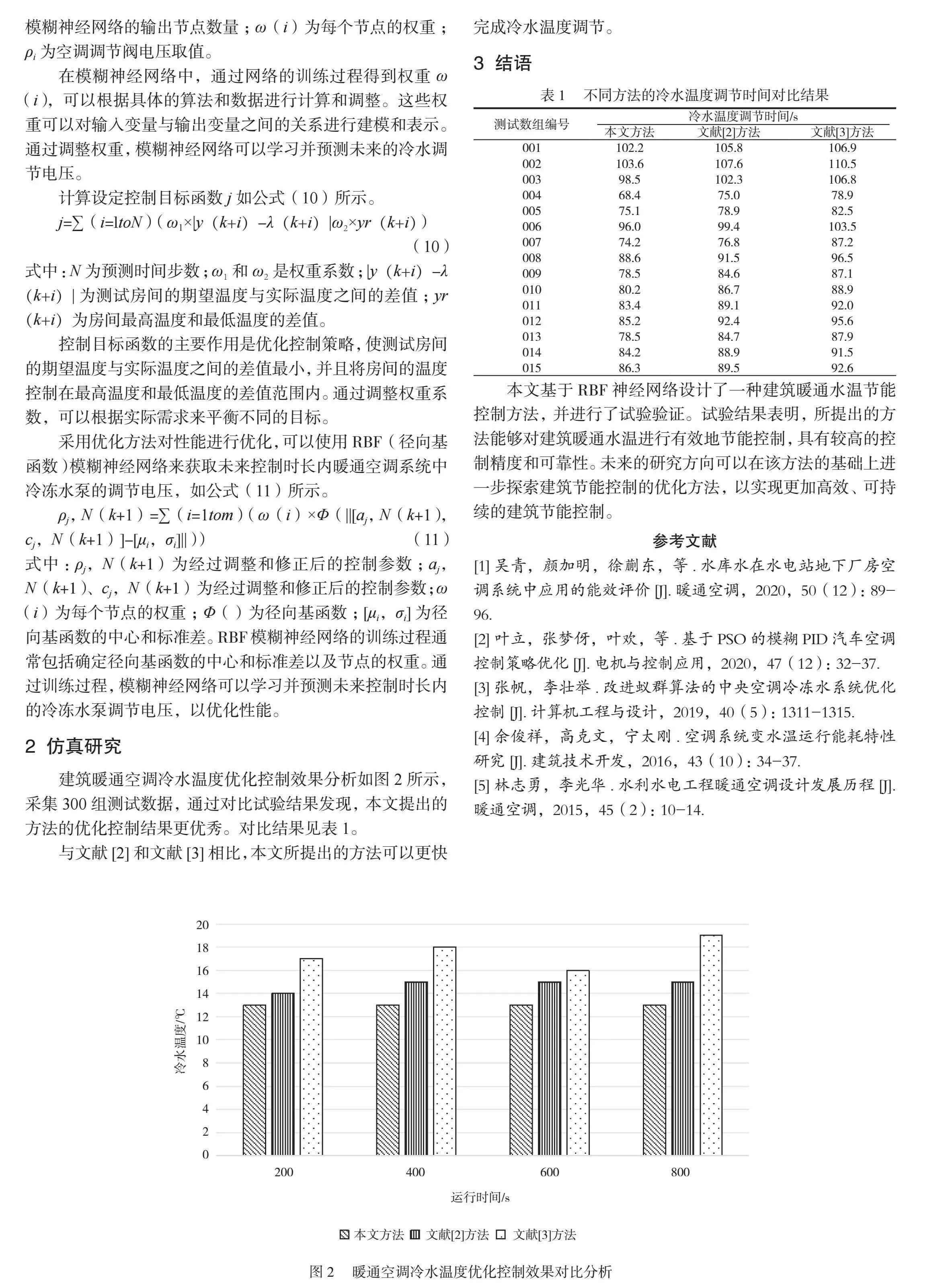
建筑暖通空调冷水温度优化控制效果分析如图2所示，采集300组测试数据，通过对比试验结果发现，本文提出的方法的优化控制结果更优秀。对比结果见表1。

与文献[2]和文献[3]相比，本文所提出的方法可以更快完成冷水温度调节。

3 结语

本文基于RBF神经网络设计了一种建筑暖通水温节能控制方法，并进行了试验验证。试验结果表明，所提出的方法能够对建筑暖通水温进行有效地节能控制，具有较高的控制精度和可靠性。未来的研究方向可以在该方法的基础上进一步探索建筑节能控制的优化方法，以实现更加高效、可持续的建筑节能控制。

参考文献

[1]吴青，颜加明，徐蒯东，等.水库水在水电站地下厂房空调系统中应用的能效评价[J].暖通空调，2020，50（12）：89-96.

[2]叶立，张梦伢，叶欢，等.基于PSO的模糊PID汽车空调控制策略优化[J].电机与控制应用，2020，47（12）：32-37.

[3]张帆，李壮举.改进蚁群算法的中央空调冷冻水系统优化控制[J].计算机工程与设计，2019，40（5）：1311-1315.

[4]余俊祥，高克文，宁太刚.空调系统变水温运行能耗特性研究[J].建筑技术开发，2016，43（10）：34-37.

[5]林志勇，李光华.水利水电工程暖通空调设计发展历程[J].暖通空调，2015，45（2）：10-14.