新能源发电高压配电网风险的算法研究

摘 要：本文针对跨区电能交易提出一种基于直流计划调整虚拟成本的优化方法，旨在改进跨区直流计划和日前发电计划，并以中国东北某省级电网为例进行算例分析。研究结果表明，该方法能够有效实现电力系统的经济运行和供需平衡，降低风险和成本，有助于维持整个电力系统的稳定性和可靠性。

关键词：跨区电能交易；直流计划调整；优化方法

中图分类号：TM 73" " " " " " 文献标志码：A

随着我国能源转型加速，新能源发展迎来了历史性机遇。新能源具有清洁、低碳和可再生等优点，是实现“双碳”目标的重要支撑[1]。作为一种清洁能源，利用新能源发电逐渐成为我国能源体系的重要组成部分，然而新能源却具有分布不均、波动性强以及不确定性大等特点，导致新能源供需不平衡，因此需要通过跨区电能交易，将新能源从富集地区输送到需求地区，实现新能源利用的最大化[2]。跨区电能交易是指在不同电网间进行的电力市场交易，可以提高电力系统的经济性、安全性和灵活性，促进新能源的消纳和发展[3]。然而，跨区电能交易也存在电力输送的不确定性、电网运行的复杂性以及市场机制的不完善性等风险，需要进行深入研究[4]。

因此，针对新能源发电高压配电网的风险问题，进行科学、合理且有效的风险评估是保障电力系统安全、稳定运行的重要手段。本文以中国东北某省级电网为例，针对跨区直流输电计划进行优化调整，建立了一种基于直流计划调整虚拟成本的优化方法，可以解决直流输电计划的优化调整问题。

1 直流联络优化模型建立

跨区电能交易的实施需要考虑不同地区的电网特性、电力市场规则和输电线路容量等因素，给电力系统的运行带来了风险和挑战。为了优化跨区电能交易效果，需要对跨区直流计划进行调整，其变化如公式（1）所示。

p（d，t）=p0（d，t）+∆p+（d，t）-∆p-（d，t） （1）

式中：p（d，t）为t时段的预定输送功率；p0（d，t）为优化调整后t时段的预定输送功率；∆p+（d，t）和∆p-（d，t）分别为t时段增加或者减少的输送功率。

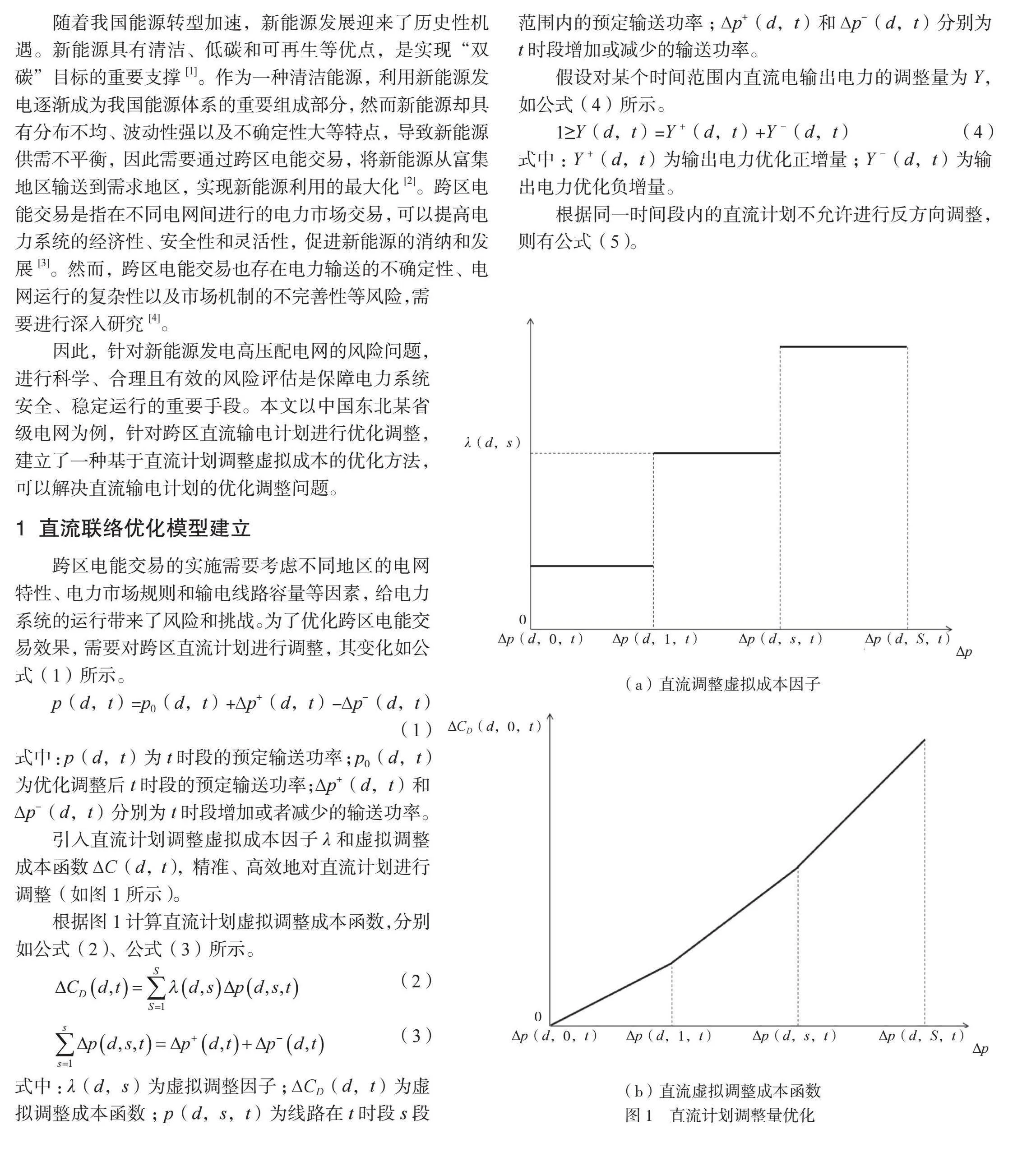
引入直流计划调整虚拟成本因子λ和虚拟调整成本函数∆C（d，t），精准、高效地对直流计划进行调整（如图1所示）。

根据图1计算直流计划虚拟调整成本函数，分别如公式（2）、公式（3）所示。

（2）

（3）

式中：λ（d，s）为虚拟调整因子；∆CD（d，t）为虚拟调整成本函数；p（d，s，t）为线路在t时段s段范围内的预定输送功率；∆p+（d，t）和∆p-（d，t）分别为t时段增加或减少的输送功率。

假设对某个时间范围内直流电输出电力的调整量为Y，如公式（4）所示。

1≥Y（d，t）=Y +（d，t）+Y -（d，t） （4）

式中：Y +（d，t）为输出电力优化正增量；Y -（d，t）为输出电力优化负增量。

根据同一时间段内的直流计划不允许进行反方向调整，则有公式（5）。

（5）

MAHER M J[5]指出输出电力优化正增量和输出电力优化负增量可在单位时间内电能转换成热量的速率的变化大小的基础上添加0、1二元变量T（d，t）来限制进行表述，如公式（6）、公式（7）所示。

D（d，t）-D（d，t-1）≤A1T1（d，t） （6）

D（d，t-1）-D（d，t）≤A1T2（d，t） （7）

式中：A1、A2为使等式满足条件的固定数值；T（d，t）为二元变量函数；D（d，t）为直流功率。

连接2个不同时间段的直流线路，其计划变化频率的限制应该是与直流线路自身的运行方式限制相匹配的，如公式（8）、公式（9）所示。

P（d，t）-P（d，t-1）≤BU+（d，t）C（t） （8）

P（d，t-1）-P（d，t）≤BU-（d，t）C（t） （9）

式中：BU为直流计划最大或最小变化速率；C（t）为研究段时长。

为了保证直流计划优化平稳进行，在最小间隔时间内，直流计划不进行进一步优化，如公式（10）所示。

（10）

式中：NT为最小间隔时间内的研究时段数量；E（d，t）为最小间隔时段内优化函数。

同样根据MAHER M J研究，BU可用0、1布尔变量E（d，t）来表述在这个时间段内是否进行优化，可得公式（11）～公式（13）。

Y（d，t+1）-M（d，t）≤E+（d，t） （11）

Y（d，t）-M（d，t）≤E-（d，t） （12）

Y（d，t）-Y（d，t+1）≤1M（d，t） （13）

式中：M（d，t）为引入的变量函数。

为保证不同地区电力市场交易正常履行，优化期间内直流电的总输出量必须符合市场交易合同规定的范围，则有公式（14）。

（14）

式中：Q（d）为直流计划优化期间最大或最小交易电量；C（t）为研究段时长。

在考虑了直流输电过程中的损失（包括变压器和线路损失）后，需要在接收端电网安全承受的上限和下限范围内对直流输送功率进行计算，如公式（15）所示。

pe-（d，t））≤D（d，t））（1-I（t））≤pe+（d，t）） （15）

式中：pe（d，t）为接受端电网能够接受的最大或者最小电力；I（t）为t时段内变压器和线路损失的损失函数。

由于2个跨区端口的电网相互依存，它们之间的电力传输需要遵循各自电网的运行规范和安全要求。同时考虑这些限制条件可以保证调整后的直流计划既满足供电端的要求，又不会对接收端的电网造成过载或不稳定的影响。

本文在上述限制的基础上，根据跨区电网的电力传输的特点，设计了2种不同的优化方法，用于改进编制供电端电网的跨区直流计划和日前发电计划，如图2所示。

根据图2所示，本文提出的双阶段优化方法基于新能源功能预测、安全约束、电力符合以及机组约束、直流计划调整约束等其他约束，对日前发电计划进行改进，同时考虑了多种影响因素，并分析了受电端口在安全条件下对直流电的最小接受能力曲线。如果受端电网直流电最低接纳能力为所有时段直流电输入的最小电量minF，如公式（16）所示。

（16）

同理最大电量maxF如公式（17）所示。

（17）

受端电网输入和输出电量达到稳定时，如公式（18）所示。

（18）

式中：L（t）为输入端电网在t时刻接收的净功率。

根据SCUC算法可得可再生能源产能源极限产值，如公式（19）所示。

（19）

式中：C为发电机在运转期间消耗的能源；Cst为发电机运行或者停止所需要的成本；ΔCW为风力或太阳能等资源的变化造成电力过剩时的遗弃成本；W为可再生能源发电机的总数。

直流计划优化虚拟费用和发电费用间的关系如公式（20）所示。

C（i，t）lt;∆CD（d，t）lt;∆CW（w，t） （20）

2 算例分析

本文以中国东北某省级电网为例进行分析，综合考虑受端电网安全等约束条件后的受端电网的直流安全接纳范围如图3所示。根据图3可知，受端电网全天可吸纳的直流输送功率高达4000MW，足以满足大部分电力需求，但白天高峰时段的电力需求旺盛，需要至少3000MW的直流注入才能满足负荷需求。凌晨时段，系统具备充分的调节余地，直流注入功率的变化不会严重影响系统平衡，系统有足够的空间进行调节，以保持电网稳定运行。由于不考虑调峰，因此导致电网早晚备用不足，需要限制风电出力。如果电网的备用容量不足，将无法满足电力需求，可能会导致电力供应中断。因此，为了保证电网的稳定运行，需要考虑调峰问题，增加电网的备用容量，以便在高峰期间满足负荷需求。说明需要在电网设计和运行中充分考虑电力需求的变化和如何有效调节电力供应，以满足这些需求。同时，应加强对风电出力的限制，避免电网早晚备用不足情况的发生。风电是一种可再生能源，具有环保、清洁等优点，但其出力受风速等自然条件的影响，存在一定的不稳定性，需要对风电出力进行有效控制，以保证电网的稳定运行。综上所述，电网的稳定运行需要充分考虑和平衡各种因素，包括电力需求的变化、电源的稳定性以及备用容量的充足程度等。

本文采用日前发电计划协调优化方法对送端电网进行优化，优化前、后的直流送出计划如图4所示。

根据图4可知，通过本文的优化调整，送端电网日前计划接受可再生能源发电量从302600MW·h增至308100MW·h。优化后，系统调节能力提高，有利于更好地消纳新能源，表明优化方案可有效增强电网的灵活性和适应能力，并有效整合和利用可再生能源。同时，为了进一步提高电网的灵活性和适应能力，可以考虑增加电网的备用容量，以便在高峰期间满足负荷需求。

3 结论

为了满足跨区域电力系统的经济运行和供需平衡，降低风险和成本，本文以中国东北某省级电网为例进行分析，针对跨区直流输电计划进行优化调整，得到以下4个结论。1）本文建立了跨区电能交易模型，并评估了跨区电能交易对电力系统的经济效益。结果表明，跨区电能交易可以有效平衡区域间的电力供需差异，提高新能源的消纳水平，降低电力系统的运行成本，增加电力系统的运行安全性和灵活性。2）本文考虑了直流计划调整对电力系统运行的影响，将直流计划调整虚拟成本作为直流计划优化的目标函数，建立直流计划调整优化模型，求解了最优直流计划调整量，并通过案例验证了所提方法的有效性和优越性。3）本文考虑了直流计划优化的多种限制条件，包括直流换流器的运行特性、直流计划的变化频率和幅度、直流计划的交易约束、直流输送功率的容量限制以及受端电网的接纳能力等，保证了直流计划优化的可行性和安全性。4）本文设计了2种不同的优化方法，分别为阶段1和阶段2，用于改进编制供电端电网的跨区直流计划和日前发电计划，实现了节能发电和新能源消纳的目标。

参考文献

[1]黄瑜珈.风电新能源及其并网探讨[J].光源与照明，2022（9）：229-231.

[2]汝小芳，赵媛.新能源开发与我国能源的可持续发展[J].能源研究与利用，2003（4）：4-6.

[3]周永华.论高压输电线路杆塔施工过程的技术要点[J].通讯世界，2014（4）：59-60.

[4]陈浩斌.高低压配电设备故障及其处理措施[J].中国新技术新产品，2018（17）：64-65.

[5]MAHER M J.Model building in mathematical programming[J].

Journal of the operational research society，2017，30（2）：182-183.