聚集核心素养，深度挖掘题目本质

笔者布置了人教版八年级数学下册第69页第14题让学生课后练习，批阅时发现了很多不同的证明思路和变式，引起笔者的重视，于是认真研究了此题，在班级进行了小结和归纳，整理汇总，与大家分享。

一、题目呈现

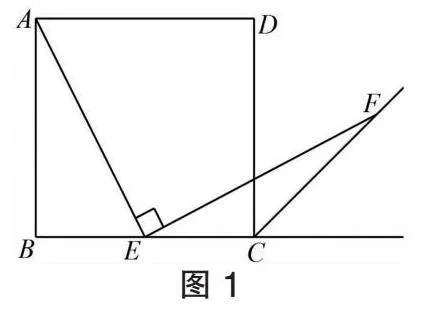
本题是人教版八年级数学下册第69页第14题：如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角的平分线CF于点F.求证：AE=EF.

难点分析：本题在正方形的背景下，综合考察正方形的性质、三角形全等的判定、证明线段相等的方法、平行四边形的判断与性质等等。解决本题要添加辅助线，要求学生具备较强的综合分析能力。

二、探究解法，挖掘题目本质，提升学生数学素养

一道题目，有时可能有多种解法，我们要从不同视角下对问题进行剖析和探究，深度挖掘题目的已知条件，添加合适的辅助线，如本题，有以下的解法：

解法1：如图2，在BA上取一点M，使BM=BE，连ME.构造△AME≌△ECF，得到AE=EF.

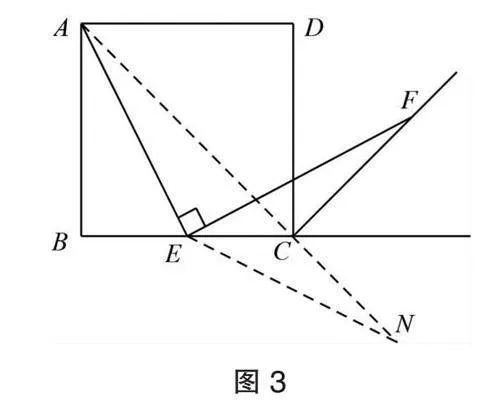
解法2：如图3，连接AC并延长，在延长线上取一点N，使得EN=EA，连EN，构造△ECN≌△ECF，得到AE=EF.

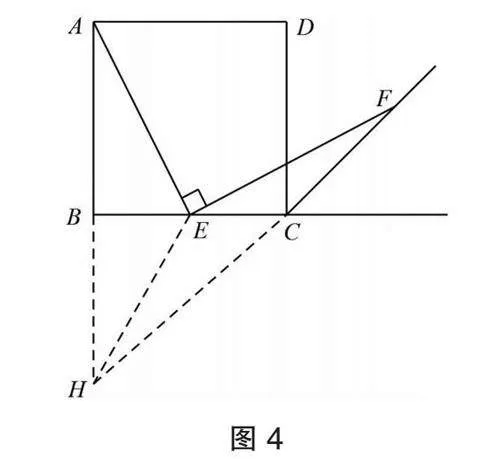
解法3：如图4，延长AB、FC交于点H，连HE，证EB垂直平分AH，得EA=EH，证∠EFC=∠EHF，得EH=EF，得到AE=EF.

解法4：如图5，连CA，过点E作QE⊥CB于点E，交AC于点Q，可得△QAE≌△CFE，推出AE=EF.

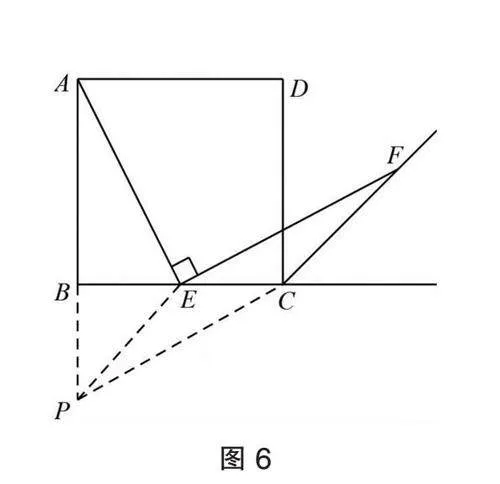
解法5：如图6，延长AB至点P，使PB=EB，连PE、PC，构造△ABE≌△CBP，证四边形EFCP是平行四边形，得到AE=EF.

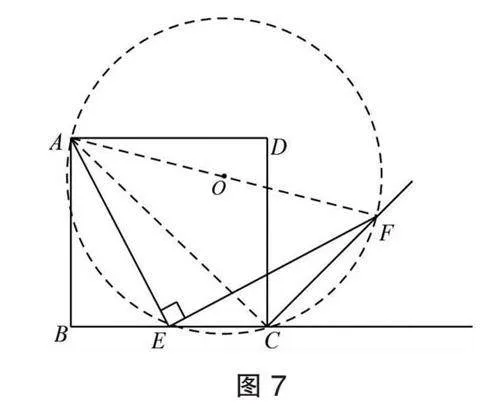
解法6：如图7，连CA，能证得∠ACF=∠AEF=90°，从而可以证得A、E、C、F四点共圆，得到∠AFE=∠ACE=45°，所以AE=EF.

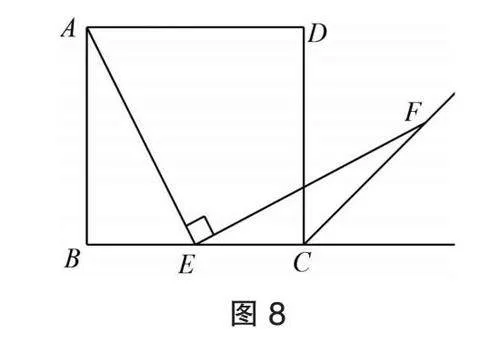
解法7：如图8，利用正弦定理，已知△ECF的两个角和一条边，可以求出EF，最后证到AE=EF.

解法8：建立平面直角坐标系，可以求出AE、EF的长度，用代数的方法研究几何.以点B为原点，BC为x轴正方向，BA为y轴正方向，BE为单位长度，建立平面直角坐标系如图9，可得：A（0，2）、E（1，0）、C（2，0），AE=，由∠AEF=90°可以推出：kAE·kEF=－1，因为kAE=－2，所以kEF=，可以求出直线EF的解析式：y=x－. 因为CF平分正方向外角，直线CF的斜率为1，且过点C（2，0），所以可以求出直线CF的解析式为：y=x－2，求出交点F的坐标（3，1），∴EF=，所以AE=EF.

三、变式拓展，激活数学思维

变式，在保留题目的本质因素下，通过题设变化、结论变化及引申，通过变化问题的内容或形式等，促进学生掌握问题的实质的一种教学方式。通过变式练习，不仅使学生对知识的理解更加深刻，更能发散学生的思维，实现举一反三的学习效果，提升学生的核心素养。

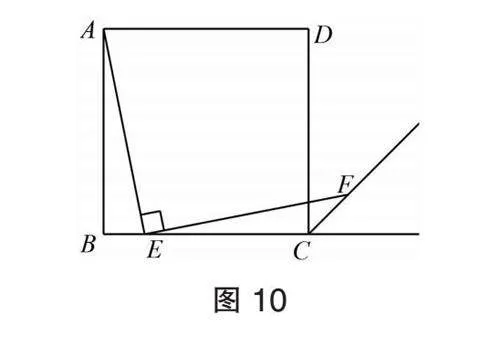
变式一：如图10，四边形ABCD是正方形，点E是边BC上的一个动点，∠AEF=90°，且EF交正方形外角的平分线CF于点F.求证：AE=EF.

变式二：如图11，四边形ABCD是正方形，点E是直线BC上的动点，∠AEF=90°，且EF交正方形外角的平分线CF于点F.求证：AE=EF.

变式三：如图12，等边△ABC中，点E是直线BC上的动点，∠AEF=60°，且EF交等边三角形外角的平分线CF于点F.求证：AE=EF.

四、感悟

1.平移、旋转、轴对称是基本的图象变换，常常借助于这些基本的图象变换构造三角形全等，达到证明线段相等、角相等的目的。解题时一定要挖掘题目已知条件，注重知识之间的关联，合理添加辅助线。

2.一题多解，拓展学生的做题思路。一道题目从不同视角下进行剖析和探究，可以有多种解法，让学生学会从不同度发现问题，发展学生的应用意识和创新意识。

3.一题多变，突出通性通法。题目从正方形出发，拓展到正n边形为背景下的动点问题，大大激发了学生的发散性思维，同时紧扣题目的已知条件，抓住问题的实质，认清题目的本质，解决问题的思路和方法不变，突出通性通法。

【注：本文系广东省教育科学规划2022年度中小学教师教育科研能力提升计划项目课题“深度学习视角下的高中数学单元教学设计的案例研究”（项目编号：2022YQJK015）研究成果】

责任编辑 邱 丽