无人机编队的无源定位及调整策略研究

摘 要：针对无人机集群圆形编队的无源定位问题，建立漂移圆模型进行无人机的方位调整，通过模拟退火算法不断优化调控，使得无人机集群保持良好的编队。利用MATLAB进行仿真，验证模型的有效性，为无人机集群的编队方位调整策略提供有益的参考。

关键词：无人机;编队方位;漂移圆模型;模拟退火算法;无源定位

中图分类号：V279 文献标志码：A 文章编号：2095-2945（2024）34-0044-04

Abstract： Aiming at the passive positioning problem of circular formation of UAV （or drone） clusters， a drift circle model is established to adjust the direction of drones， and the simulated annealing algorithm is used to continuously optimize and control， so that the drone cluster maintains a good formation. Simulation using MATLAB verifies the effectiveness of the model and provides a useful reference for the formation orientation adjustment strategy of UAV clusters.

Keywords： unmanned aerial vehicle（UAV）; formation bearing; drift circle model; simulated annealing algorithm; passive location

随着世界科技水平的发展，无人机在军用与民用领域都有了大量的应用场景，尤其是无人机集群可利用规模效应，进行协同作业，优势明显。为了保障无人机群编队的系统精度和安全性，编队飞行过程中的无人机无源方位调整就显得非常重要。

在无人机遂行编队飞行中的纯方位无源方位调整方面，杨雨卉等[1]提出基于理想圆的标准角度调整模型来解决圆形编队方位调整，基于理想等边三角形的调整模型来解决锥形编队方位调整。李汉森等[2]提出利用滑动均值法进行无人机纯方位无源调整，利用正弦定理和三角函数推导出变量之间的函数关系。聂础辉等[3]提出通过角度信息构建位移算法，通过动态迭代的方式，灵活选择方向信息最接近理想值的无人机作为下次迭代时的第三台发射机，经过多次迭代直至收敛。潘礼规等[4]侧重于对无人机编队阵列布局的研究，得出“面”布局可提升无人机定位性能，合理配置观测几何能提高相对定位精度。刘高峰等[5]通过最小二乘法求出近似解，并运用多步决策模型逐渐调整无人机位置保持编队的有效性。

本文针对无人机编队飞行过程中存在的方位偏差问题，建立漂移圆模型，由于模拟退火算法较易实现，且能很好地适应非线性复杂问题，采用模拟退火算法优化无人机方位调整模型，确保无人机集群飞行过程中编队始终保持合理的队形。

1 无人机定位模型

以圆形编队的无人机集群作为研究对象，除圆心无人机外，其余无人机均匀分布在圆上，编队中每架无人机均有固定编号，且在编队中与其他无人机的相对方位关系保持不变。假定无人机飞行过程不受外界因素干扰、收信机能实时接收到发信机的信号、无人机真实位置与理想位置偏差不会太大、编队飞行在统一水平面上。由此得到无人机编队示意图如图 1所示，设包含圆心机在内的无人机总量为Z台，无人机圆周半径为R，除了圆心机FY00外，其余无人机均匀分布在圆周上。取FY00和任意2台编号为X1、X2的无人机为发信机，FY00与X1的连线方向为直角坐标X轴正方向，选取任意一台收信机Y，此时X1、X2与Y满足

X1，X2，Y∈[1，Z-1] 。 （1）

设收信机Y的定位方位角是（α1，α2），如图1所示。由于（α1，α2）唯一且互不相同，因此确定的（α1，α2）可实现对Y的定位。

以圆心为角的顶点，Y与X1、X2的夹角分别是（β1，β2），由图1可知

αi=，i=1，2 ， （2）

βi=×Xi-Y，i=1，2 。 （3）

由于（α1，α2）与（β1，β2）构成映射关系，因此确定的（β1，β2）可实现对Y的定位。

在无人机编队飞行过程中，收信机Y的实际位置可能会与理想位置之间存在偏移，两者之间的偏差可以用无人机位置的半径偏差σ和角度偏差θ来衡量。

σ=r-r′ ， （4）

θ=β1-β1′ 。 （5）

2 无人机漂移圆模型

为了确保无人机形成理想编队，需要在无人机编队飞行过程中，控制无人机位置的半径偏差σ和角度偏差θ减小至合理范围内。

使用2架发信机X1与X2对具有一定偏差的无人机Y'（理想方位为Y）进行调整，利用三点构建漂移圆模型，如图2所示。由X1、X2、Y三点构建的圆心为O点，由X1、X2、Y′三点构建的圆心为O′点。

设X1、X2、Y三点的坐标分别为（x1，y1）、（x2，y2）、（x3，y3），圆心O为（x，y），圆心为O′为（x′，y′），由几何关系可得

利用公式（6）也可以推导出（x'，y'），进而得到两圆心距离OO'，只要设计方案缩短OO'至极小值，就可确保Y'与其理想方位Y的偏差在允许范围内，满足编队飞行的要求。

3 基于模拟退火算法的方位调整策略模型

模拟退火算法具有算法较易实现，能很好地适应非线性复杂问题，可以通过随机因素向全局最优解方向搜索的优点[6]，因此其适用于无人机编队的方位调整。本文采用模拟退火算法对漂移圆模型进行求解和调控。

基于漂移圆模型，获取无人机的方位信息，进而得到能量函数E

E=，（7）

式中：n为迭代次数，En_X、En_Y为偏差欧氏距离

En_X=Xreal-Xideal;（8）

En_Y=Yreal-Yideal。（9）

利用模拟退火算法进行求解。退火过程中，用f（X）表示当前状态，f（X+1）表示下次迭代后状态，f（X*）表示变化了的状态量。令无人机沿实际方位与理想方位间特定轨迹的2个方向移动特定步长，计算相应的适应定值，若能量E下降，通过比较选取E更接近于全局最优解进行迭代。根据Metropolis准则，定义系统由f（X*）变为f（X+1）的接收概率为P

式中：K为Boltzmann常数，Tn为系统当前温度。

在迭代过程中，系统的绝对温度缓慢下降，表示为

Tn+1=λ×Tn ， （11）

式中：λ为退火系数，取值0到1之间。

经过n次迭代后，寻找最低偏差方位，能量E接近于全局最优解，达到终止温度，退火操作完成，无人机调整至理想方位。

4 仿真试验

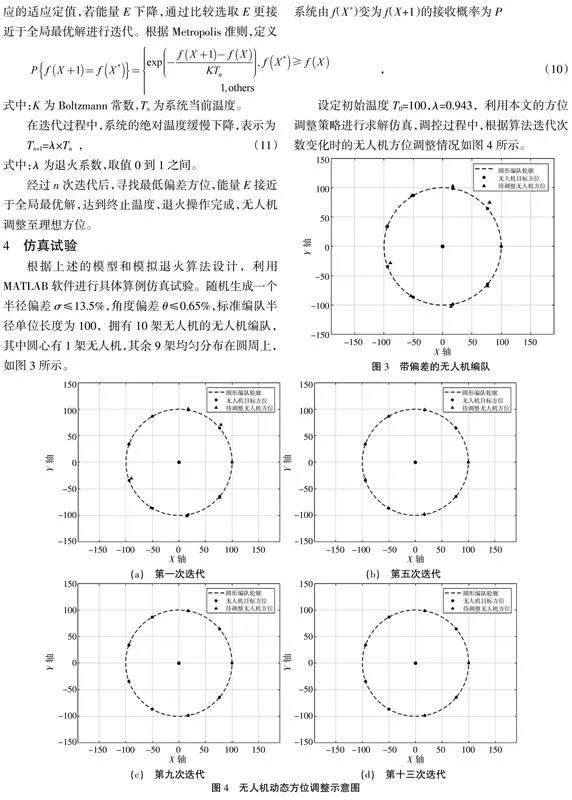
根据上述的模型和模拟退火算法设计，利用MATLAB软件进行具体算例仿真试验。随机生成一个半径偏差σ≤13.5%，角度偏差θ≤0.65%，标准编队半径单位长度为100，拥有10架无人机的无人机编队，其中圆心有1架无人机，其余9架均匀分布在圆周上，如图3所示。

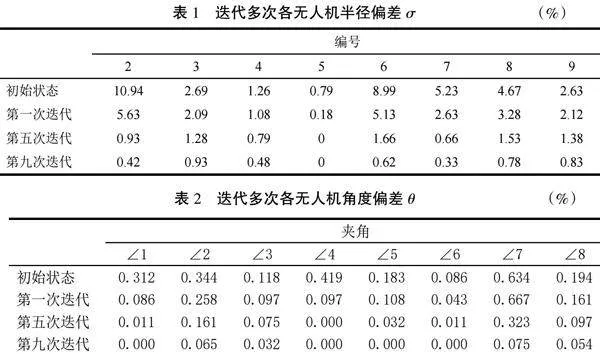
设定初始温度T0=100，λ=0.943，利用本文的方位调整策略进行求解仿真，调控过程中，根据算法迭代次数变化时的无人机方位调整情况如图4所示。

由图4可知，初次迭代时部分无人机有明显的方位偏差，经过5次迭代之后，无人机实际位置与理想位置偏差已经很较小，9次迭代之后直观上已经很难分辨出来实际位置和理想位置。

为了进一步说明偏差的变化情况，表1和表2分别给出了迭代过程总的半径偏差和角度偏差的变化值。

由表1可知，8架无人机中，对于半径偏差σ，在迭代之前，其最大值为10.94%，均值为4.65%;在迭代9次后，其最大值为0.93%，均值为0.445%，表明9次迭代后，全部无人机的半径偏差均降低至小于1%，相对于半径长度为100个单位，半径偏差均在一个单位距离以下，且均值在半个单位距离以内，半径偏差非常小。

由表2可知，8架无人机中，对于角度偏差θ，在迭代之前，其最大值为0.419%，均值为0.286%;在迭代9次后，其最大值为0.075%，均值为0.028 2%，表明9次迭代后，角度偏差非常小。

结合图4和表1、表2，在模型迭代9次后，无人机实际位置与理想位置之间的偏差已经很小;迭代13次，两者几乎没有偏差。从仿真试验结果上看，此调整方法具有较高的准确性。

5 结论

本文针对无人机遂行编队飞行中的纯方位无源方位调整问题开展研究，建立了衡量无人机实际方位与理想方位偏差的漂移圆模型，设计了模拟退火算法进行方位调整，并且通过MATLAB进行了仿真试验验证。仿真结果表明，对于随机生成的无人机圆形编队，依据模型迭代9次后，全部无人机的半径偏差和半径偏差均明显减小，此时无人机实际位置与理想位置之间的偏差已经很小，通过方位调整策略保证了无人机编队飞行过程中的队形不变，验证了模型和算法设计的有效性。

本文只考虑了二维平面圆形均匀分布无人机编队的方位情况，没有考虑到实际编队中三维方位可能导致的全局偏差问题，今后将完善模型来消除这种偏差产生的影响。

参考文献：

[1] 杨雨卉，于爱菊，乔琛.无人机遂行编队飞行中的纯方位无源定位方案研究[J].数学建模及其应用，2023，12（1）：60-68.

[2] 李汉森，曹健铭，张育涛，等.基于滑动均值法的无人机纯方位无源调整策略[J].数字技术与应用，2023，41（6）：39-43.

[3] 聂础辉，曾慧林，黄逸桓，等.无人机遂行编队飞行中的纯方位无源定位[J].湖南理工学院学报（自然科学版），2023，36（2）：17-20.

[4] 潘礼规，尹佳琪，徐春光.一种无人机集群相对定位新方法及编队队形影响分析[J].兵工自动化，2023，42（10）：84-91，96.

[5] 刘高峰，臧秋艳，李燕珊，等.一种高精度无人机编队纯方位无源定位方法[J].科技创新与应用，2024，14（10）：143-146.

[6] 邓绍强，郭宗建，李芳，等.基于Metropolis准则的自适应模拟退火粒子群优化[J].软件导刊，2022，21（6）：85-91.

基金项目：广东省一流本科课程“电机学”项目（粤教高函〔2022〕10号）;广东省一流本科课程“发电厂电气部分”项目（粤教高函〔2023〕33号）;广东省本科高校教学质量与教学改革工程建设项目（粤教高函〔2024〕9号）;华南农业大学本科教学质量与教学改革工程项目（JG2023028）;华南农业大学课程思政示范课程“电机学”项目（kcsz2023011）;广东省省级大学生创新训练项目（S202410564069）

第一作者简介：邓孟龙（2001-），男。研究方向为电气工程及其自动化。

*通信作者：孔莲芳（1979-），女，博士，讲师。研究方向为智能电力系统、控制理论与工程。