基于混沌理论和RBF神经网络算法的风电功率预测研究

摘要：风电功率预测对并网后电力系统的发电量调度、优化以及安全稳定地运行具有重要意义。通常算法是通过分析风功率与天气因素的关系等方法来预测的，没有从风机发电系统的角度出发。因此，传统算法使用的数据种类较多，导致模型的训练压力较大，且容易陷入局部极小值点，影响预测结果。由于风力发电时间序列具有混沌特性，本文将混沌理论与RBF神经网络结合应用至风电功率预测中。本文采用宁夏长山头风电场数据进行了训练与预测，并与BP神经网络模型进行对比，结果显示，混沌RBF神经网络取得了良好的效果，提高了超短期预测的预测精度。

关键词：风功率预测；混沌理论；相空间重构；RBF神经网络

引言

鉴于风的波动性和非连续性特征，当大规模风电并入电网系统时，将给电力系统的安全稳定运作及电能质量构成严峻考验[1]。鉴于此，开展风电功率预测显得尤为重要。借助风力发电功率的超短期预测技术，能够有效促进电网运行状态的即时动态调整，并合理规划传统能源的发电输出，确保电网供电量与用户需求负荷之间维持均衡，从而保障电力系统的平稳运行[2-3]。

目前，预测技术可分为两类：物理建模技术和统计建模技术[4]。物理建模技术是基于数值天气，考虑风电场的具体地理环境如地形、等高线、障碍物等，结合机组的功率时序进行预测，但这类方法建模时考虑因素较多，预测精度受到一定影响；统计建模技术较少考虑风速变化的物理过程和风电场的具体地理信息，而是根据风电功率时间序列寻找天气数据与风电场出力的关系，根据这种函数关系来预测发电场未来时刻的出力情况[5]。这类预测模型是利用大量的历史数据建立输入与输出之间的映射关系，可以提高预测精度[6]。小波分析法是一种空间分析法，通过对风功率序列进行多尺度分解，能够有效弱化风功率的随机性强、波动幅度较大的特点，较好地提高了预测精度。但小波变换中选取合适的小波基与确定分解尺度方面有一定的难度，影响小波分析法的预测精度。支持向量机法在解决非线性问题方面很有优势，但存在确定网络结构的困难以及局部极小值点的问题，影响预测精度的提高[7]。针对这些问题，本文提出了混沌RBF神经网络的预测方法。

鉴于风力发电功率时间序列展现出混沌特性[8]，混沌理论为风电功率预测开辟了一条新途径。该途径通过运用混沌理论的相空间重构技术，将风力发电功率的一维时间序列转换至高维相空间中进行重构，以此方式，一维时间序列中的信息更为充分地在高维空间中得到体现，进而能更深入地挖掘时间序列隐含的信息并重建系统的动态路径。在此过程中，确定运动轨迹中各点连接函数的近似表达，即解决逼近非线性函数的问题，成为整个过程中的核心环节。人工神经网络（ANN）[9]通过内部训练调整权系数找到输入与输出数据之间的非线性映射关系，这种独特的处理非线性时间序列的能力被广泛应用到风电功率预测中。功率时间序列经过相空间重构后应用RBF神经网络能更好地逼近非线性函数的映射，提高了预测精度。本文采用宁夏长山头风电场数据进行了训练与预测，并与BP神经网络模型进行对比，结果显示，混沌RBF神经网络取得了良好的效果，提高了超短期预测的预测精度。

1. 风功率时间序列的相空间重构

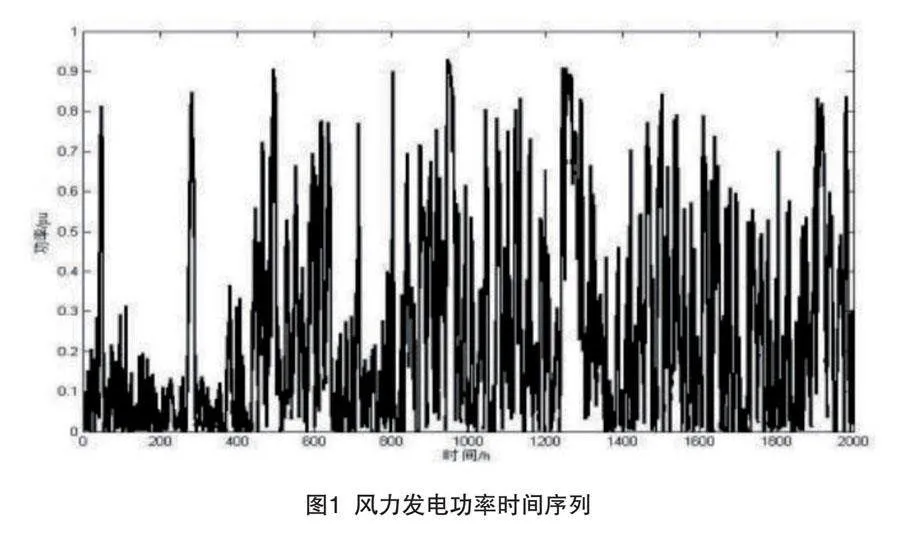
风力发电功率具有随机波动性和间歇性，如图1所示。利用混沌理论的相空间重构法对一维风功率时间序列进行重构，从而研究出风力发电系统的结构性，即恢复出该系统的演化轨迹。塔肯斯定理证明了由一维风功率观测序列以及选取合适的延迟时间与嵌入维数，对风功率序列进行相空间重构，风力发电系统的运动轨迹可由重构后相空间中的相点的演化轨迹完整地恢复出来[10]。

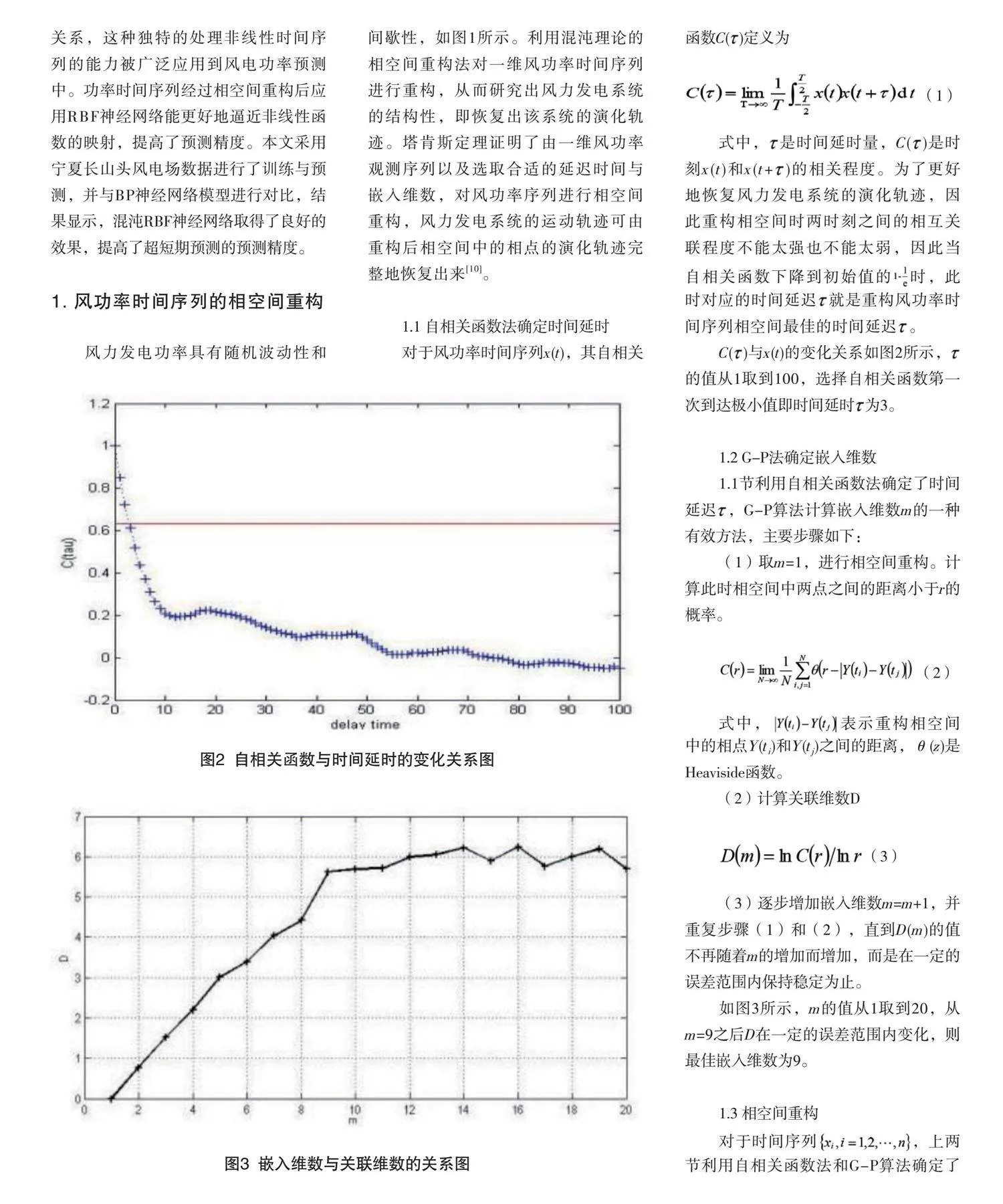
1.1 自相关函数法确定时间延时

对于风功率时间序列x（t），其自相关函数C（）定义为

（1）

式中，是时间延时量，C（）是时刻x（t）和x（t+）的相关程度。为了更好地恢复风力发电系统的演化轨迹，因此重构相空间时两时刻之间的相互关联程度不能太强也不能太弱，因此当自相关函数下降到初始值的时，此时对应的时间延迟就是重构风功率时间序列相空间最佳的时间延迟。

C（）与x（t）的变化关系如图2所示，的值从1取到100，选择自相关函数第一次到达极小值即时间延时为3。

1.2 G-P法确定嵌入维数

1.1节利用自相关函数法确定了时间延迟，G-P算法计算嵌入维数m的一种有效方法，主要步骤如下：

（1）取m=1，进行相空间重构。计算此时相空间中两点之间的距离小于r的概率。

（2）

式中，表示重构相空间中的相点Y（ti）和Y（tj）之间的距离，θ（z）是Heaviside函数。

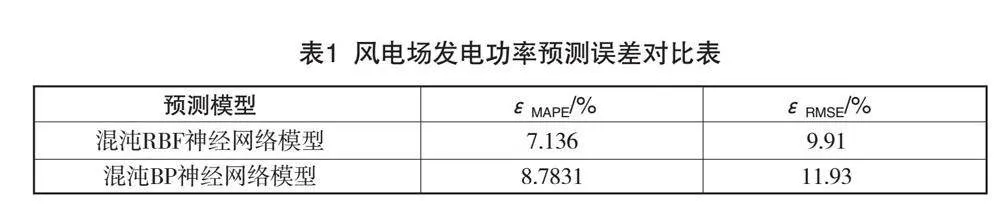
（2）计算关联维数D

（3）

（3）逐步增加嵌入维数m=m+1，并重复步骤（1）和（2），直到D（m）的值不再随着m的增加而增加，而是在一定的误差范围内保持稳定为止。

如图3所示，m的值从1取到20，从m=9之后D在一定的误差范围内变化，则最佳嵌入维数为9。

1.3 相空间重构

对于时间序列，上两节利用自相关函数法和G-P算法确定了相空间重构所需要的嵌入维数m和延迟时间，则重构相空间的吸引子矩阵为

（4）

2. 混沌RBF神经网络预测模型的确定

2.1 相空间重构和RBF神经网络结合的理论依据

当前，BP神经网络与RBF神经网络被广泛应用。具体而言，BP神经网络在训练过程中运用负梯度下降算法来调整其权重系数，这一机制导致BP神经网络存在收敛速度较慢且易于陷入局部最优解的困境；相比之下，RBF神经网络凭借其独特的最佳逼近性质，能够高效地实现非线性关系的映射。在众多前馈网络中，RBF网络被视为执行映射功能的最佳选择，其学习过程不仅收敛迅速，而且有效避免了局部最优解的问题。鉴于此，本文选用RBF神经网络。

RBF神经网络的特性使其极为适用于混沌序列的预测研究领域。应用混沌理论使得原本一维的风功率序列在高维相空间中得以映射，进而展现出风力发电机出力系统的动态行为特征。借助RBF神经网络对高维相空间内的相点进行函数逼近，能够揭示出该动力系统的函数关系，基于这一关系，可以预测系统未来的状态点位置。

在上文中，针对风功率时间序列，实施了相空间重构。通过确定两个相点间的函数关系，能够精确地描绘出系统的运动轨迹，并据此推断出系统下一个状态点的位置，这等同于获取了未来某一时刻的信息，而这种函数关系通过RBF神经网络学习训练后得到[11]。

（5）

该过程涉及将一个m维相空间中的信息投影至一维时间序列的非线性变换，寻找这样的函数关系颇具挑战性。幸运的是，神经网络凭借其强大的输入－输出非线性映射能力，恰好能够有效应对这一难题[12]。

2.2 混沌RBF神经网络预测模型

首先，利用相空间重构方法恢复风功率时间序列所代表的系统运动轨迹，并据此构建出重构相空间的吸引子矩阵，该矩阵包含了所有相点的信息。然后，将这一重构后的样本空间（即吸引子矩阵）作为RBF神经网络的输入数据。通过神经网络的训练过程，能够逼近相点与其后续点之间的函数关系F（x），从而实现对未来值的预测。预测流程图如图4所示。

（1）为方便后续的计算，对功率时间序列进行归一化处理；

（2）利用相空间重构法对归一化之后的风电功率时间序列进行前期数据处理，找到合适的和m，完成相空间重构；

（3）应用Wolf法计算最大Lyapunov指数λ，判断该序列是否具有混沌属性；

（4）用RBF神经网络通过训练学习数据来拟合满足公式（5）的这种函数关系，然后利用训练好的神经网络来推导未来的值，即用时间序列的前m个值（x（t），x（t+），…，x（t+（m-1）））来预测下一个值x（t+1+（m-1））。

对于实际风功率短期预测模型，RBF神经网络的学习样本输入即风功率历史数据相空间重构后的向量见公式（6），学习样本输出即训练目标见公式（7），即

（6）

（7）

RBF神经网络的训练部分的核心是神经元节点间连接权值的调整，并且找到最优权系数的问题。通过调整神经元节点间的阈值和权值，直至收敛为止。最后得到网络固定的阈值、权值和样本数据相对应的系统模型。

3. 算例分析

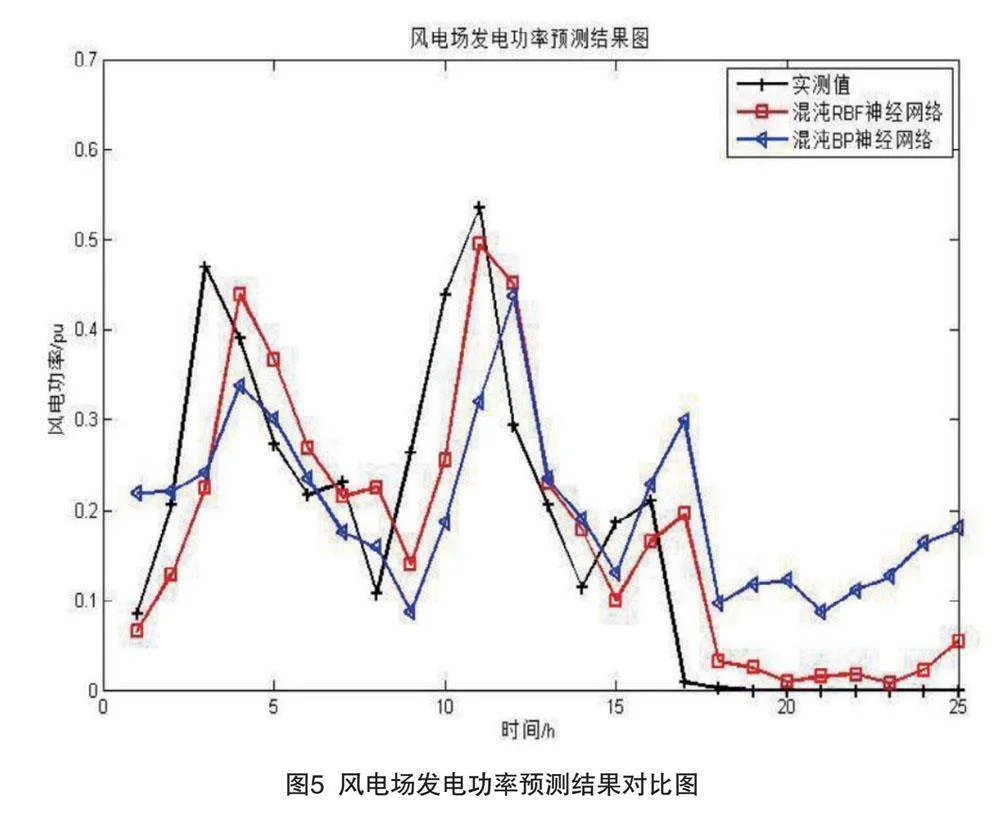
以宁夏长山头风电场2018年一年的数据为样本，对风电功率进行短期预测。前10个月的功率数据用来训练，后2个月的功率数据用来预测。根据前述相空间重构的结果，本文用BP神经网络法与RBF神经网络法的预测结果进行对比。预测结果对比图片段如图5所示。

如图5所示，两条预测曲线均与实测值曲线呈现相似的变化趋势。然而，相较于混沌神经网络BP模型，混沌RBF模型的预测曲线在拟合实测值变化方面表现得更为出色，特别是在功率值为零的关键点上。因此，可以得出结论，混沌RBF神经网络模型的预测性能更优。

同时εMAPE%能更好地反映预测值误差的实际情况；εRMSE%用于衡量预测误差的分散度。对预测结果进行评价，结果如表1所示。

结果显示，混沌RBF神经网络模型的εMAPE%和εRMSE%都明显低于混沌BP神经网络模型，表明RBF模型与实测值的拟合效果更好，适应性更好，预测精度更高。

综上，RBF神经网络能找到最优的权系数且收敛速度快，适应性强，鲁棒性好，预测效果稳定。RBF神经网络弥补了BP神经网络收敛速度慢和陷入局部最小值的问题。

结语

针对传统算法预测精度较低的问题，本文提出了混沌RBF神经网络预测模型，将一维的功率时间序列重构出整个系统的运行轨迹，能够揭示该时间序列内蕴含的信息；再利用RBF神经网络进行各相点间的函数逼近，确定系统的运动轨迹，以便于未来值的预测。经过算例分析并与BP神经网络模型进行对比，结果表明，将混沌理论与RBF神经网络结合的预测方法运用至发电场发电功率的超短期预测中具有较强实用性。

参考文献：

[1]匡威.基于STATCOM的并网风电场电压稳定性改善研究[D].株洲：湖南工业大学，2022.

[2]杨丽薇，高晓清，蒋俊霞，等.基于小波变换与神经网络的光伏电站短期功率预测[J].太阳能学报，2020，41（7）：152-157.

[3]韦通鑫.面向可再生能源效率提升的电网电量平衡规划研究[D].济南：山东大学，2023.

[4]黄树帮，陈耀，金宇清.碳中和背景下多通道特征组合超短期风电功率预测[J].发电技术，2021，42（1）：60-68.

[5]章雅楠，莫日格吉勒图.风力发电系统功率预测技术研究综述[J].电工技术，2023（11）：14-17.

[6]陶虎，文智江，吴晓锐.基于小波分析和改进BP神经网络的风电功率预测算法[J].广西电力，2022，45（2）：1-6，48.

[7]王涛，高靖，王优胤，等.基于改进经验模态分解和支持向量机的风电功率预测研究[J].电测与仪表，2021，58（6）：49-54.

[8]商立群，李洪波，黄辰浩，等.基于多变量相空间重构和优化深度极限学习机的短期风电功率预测[J].南方电网技术，2023，17（2）：82-91.

[9]王瑞，王雨宁，逯静.基于双分解和深度学习的短期风电功率预测[J/OL].武汉大学学报（工学版），1-16[2024-10-29].http：//kns.cnki.net/kcms/detail/42.1675.T.20241008.1139.004.html.

[10]西安理工大学.基于马尔可夫链和组合模型的风力发电功率预测方法：CN202111376441.8[P].2024-08-02.

[11]陈婷，郭亚琪，彭杰，等.基于相空间重构及模糊聚类的供电服务风险评价模型[J].自动化技术与应用，2024，43（10）：217-220.

[12]董洁，韩子扬.相空间重构与改进SMA优化SVR的网络流量预测[J].计算机工程与设计，2024，45（9）：2796-2804.

作者简介：朱莉娜，硕士研究生，助教，1285389255@qq.com，研究方向：人工智能技术应用。