指向运算教学中推理意识培养的教学实践

［摘 要］数运算本质上是严格的推理过程。从数的结构、算理及算法的一致性来看，运算是培养推理意识的基础。以人教版教材四年级上册“三位数乘两位数笔算练习课”为例，探讨运算教学中推理意识的培养方法，为进阶式培养学生的推理意识提供新的范式。

［关键词］推理意识；三位数乘两位数；运算教学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）32-0023-03

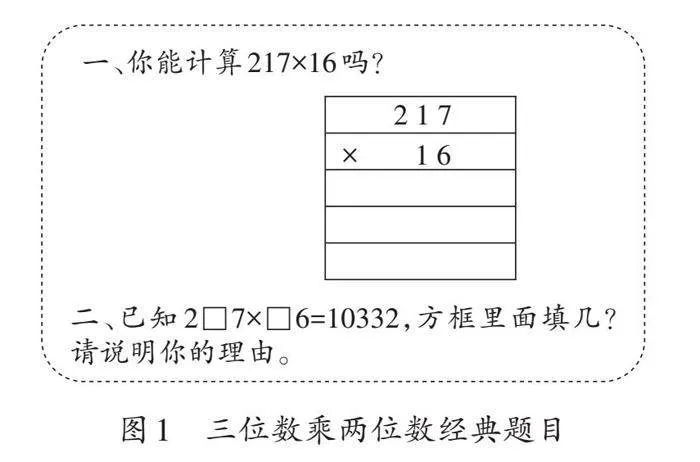
运算在数学中占据核心地位，它既是数学研究的对象，也是一种基本的思维模式。笔者利用两道三位数乘两位数的经典题目（如图1），对四、五、六年级共316名学生检测与分析（见表1），发现学生虽能熟练掌握计算技巧，但其推理能力并未随年级提升而显著增强。

面对这一现象，笔者很是疑惑：既然机器计算更为精确且迅速，为何仍需学习运算？运算教学除了提升运算能力，还应关注哪些方面？于是以人教版教材四年级上册“三位数乘两位数笔算”练习课为例进行探究。

一、提出推理意识：指向“为什么”的学生立场分析

运算学习涵盖三个核心问题：一是“如何算”，即算法与运算程序的应用，体现为运算的熟练度；二是“为何这样算”，即对算理的理解，体现为运算的合理性；三是“怎样算更好”，即算法的优化，体现为运算的灵活性。简而言之，学生需会计算、会说理、会运用。其中，“会运用”更多的是指综合运用运算知识，体验“提出猜想—论证猜想—得出结论”的推理过程。

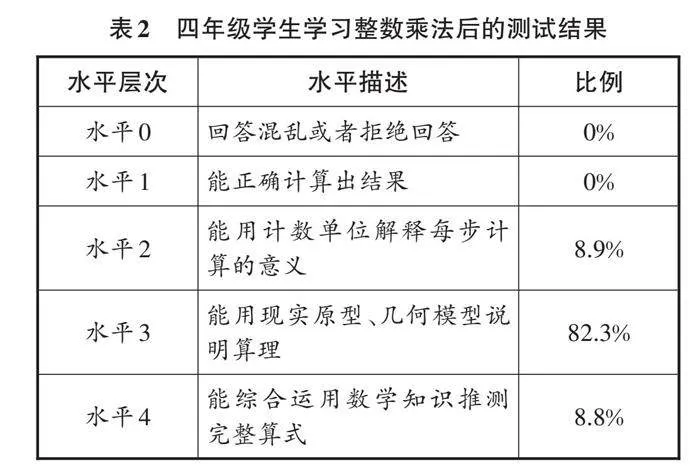
笔者根据这三个核心问题设计检测单（如图1）对本校四年级120名学生进行测试，并运用SOLO分类理论评估学生水平（见表2）。

通过分析得出以下两个启示：

第一，重视在运算教学中培养推理意识。《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）强调算理与运算的一致性，即推理的意义。表2中显示82.3%的学生达到水平3，表明他们已掌握计算和说理方法。然而，面对“2□7×□6=10332”这样的挑战，只有8.8%的学生能进行有理有据的推理。这一现象提示教师在运算教学中需加强学生推理意识的培养。

第二，强调几何模型助力推理意识培养。运算教学中，利用几何模型将抽象运算具象化，有助于学生理解算理。分析学生作品后发现，仅1.7%的学生使用了几何模型来说明算理，表明大部分学生对此方法不熟悉或不喜欢。这不利于学生对算理的理解、运算一致性的建立，以及核心素养的形成。

二、思考推理意识：明确“是什么”的整体视角解读

推理意识分为合情推理和演绎推理，它要求学生对自己和他人的问题解决过程给出合理的解释，并培养讲道理、有条理的思维习惯。在小学阶段，各种数学关系及其推理过程本质上都与数运算紧密相关。

（一）表现描述——运算中发展推理意识

2011年版和2022年版课程标准对运算能力的主要表现及教学要点有不同的描述。2022年版课程标准从定义、表现和作用等多个维度对运算能力进行了详细阐述，特别强调通过运算来促进学生数学推理意识的发展。

（二）课标指出——逐层发展推理意识

《课程标准》在数与运算的内容要求中，针对三个学段的运算教学均提出了培养推理意识的要求：第一学段，通过情境、文字和模型理解四则运算的意义和关系，初步发展推理意识；第二学段，通过学习运算律进一步发展推理意识；第三学段，通过理解数与运算概念系统的内在联系，增强运算中的推理，让学生在法则运用中体验数学从一般到特殊的论证过程。这为教师在运算教学中逐层发展学生的推理意识提供了方向。

（三）教材变化——推理意识凸显一致性

对比不同版本教材中“三位数乘两位数”练习课的内容后发现，苏教版教材引导学生使用现实模型和纯数学理论进行推理，沪教版和香港版教材则引入了几何模型，以促进推理意识的培养。同时，比较2011年版和2022年版人教版教材，可以看出2011年版人教版教材倾向于正向推理，而2022版人教版教材则更注重综合运用运算知识进行推理，要求学生运用现实模型、纯数学理论和几何模型等多种方式讲道理，对推理意识的要求更高。

综合表现、课标和教材的多维度解读，可以得出运算中的推理包括：（1）通过类比推理感悟运算的一致性；（2）通过加强算理教学形成推理意识；（3）通过注重运算间的联系发展推理意识。

三、实践推理意识：构建“怎么做”的学习路径

在教学“三位数乘两位数”后，笔者安排了一堂专注于推理意识培养的练习课：以“辨析—明理—结构”为线索，通过从精确计算到估算、从分散知识点到连续知识链、从结果准确性到数值范围的多层次教学过程，培养学生的推理意识。

（一）运用“三算”激发推理意识

本课的第一环节通过一道选择题“□□□×□□=（ ）。①998 ②6000 ③99901 ④100000”来启动。该环节围绕核心问题“你不会选择哪一个，为什么？”引导学生运用运算知识进行推理。四个选项“①998 ②6000 ③99901 ④100000”分别代表三位数、四位数、五位数和六位数的乘积，学生通过考虑最小积、最大积或特殊算式如“1000×100”来进行判断。整个推理过程包括“口算筛选—估算比较—笔算验证”，旨在让学生将“三算”内化为需求，并运用这些方法对未知算式的结果进行推理，从而激发学生的推理意识。

（二）借助几何模型提升推理意识

在激发学生的推理意识之后，笔者进一步利用“□□□×□□≈6000”这一教学素材，指导学生编写算式并阐述理由。在反馈环节，通过“初步推理—丰富推理—深化推理”三个阶段，逐步提升学生的推理意识。

第一层，初步推理。

针对“□□□×□□≈6000”，笔者提出问题“像这样的算式，你最多能列出几道”。学生从“300×20”推理出“299×20、300×21、301×20、302×20”这四个算式的积均约等于6000。笔者追问：“哪个算式的结果更接近6000？”学生通过观察乘数的变化来判断哪个算式更接近6000。在这一阶段，学生得出的答案多样，各自有各自的理由，交流出现障碍。

第二层，丰厚推理。

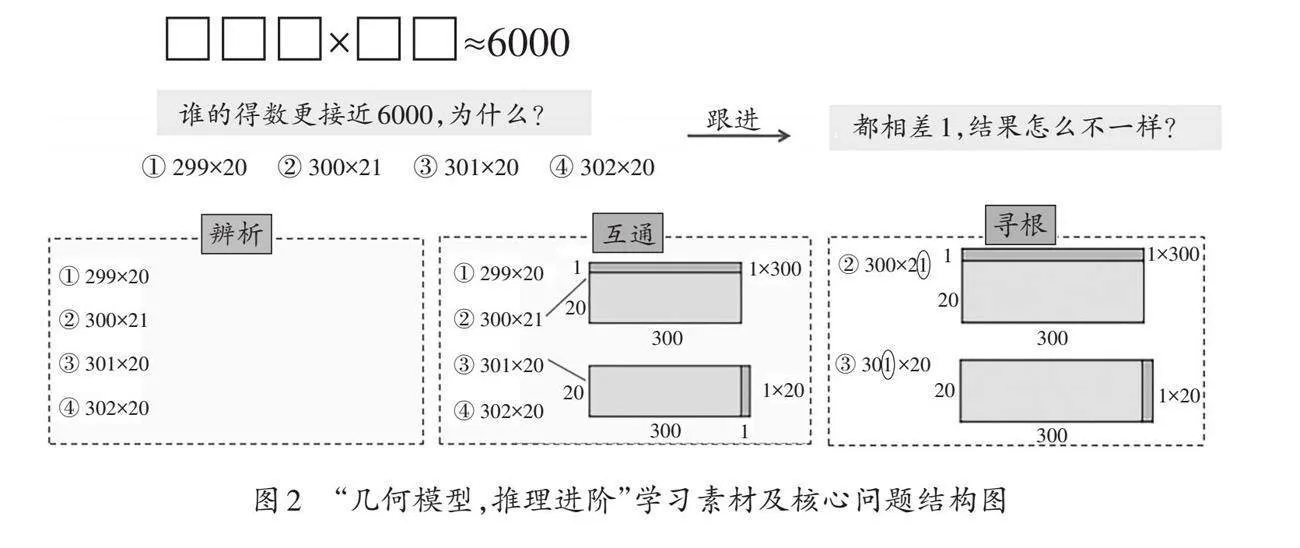
基于上述情况，笔者引导学生想象“299×20、300×21、301×20、302×20”四个算式的图形，将图形表征与语言表征相结合。在学生绘制草图后，笔者通过问题“为何相差1，结果却不同？”引导学生深入思考。这样，图形、语言与算式相互关联（如图2），使得推理有形有据。学生从关注结果的差异转向关注乘数的变化，根据乘法规则推理，弥合思维上的断点。

第三层，深化推理。

笔者提出问题：“如果一个数估大了，另一个数估小了，哪个算式更接近6000？①597×13 ②299×21 ③148×42”“你肯定不选哪一个？为什么？”学生通过绘制草图来解释自己的选择。首先，观察“597×13”的图形后，学生发现将其估成“600×10”后，多了3个597，少了3个10，从而理解积实际上增加了约1800。接着，对比“299×21”和“148×42”的图形，学生就能通过图形推理出哪个算式更接近6000。最后，学生运用笔算验证“353×17”，从而打破思维定式，丰富推理方法。

整个过程中，学生利用画图、分析、推理，明确了乘数与积之间的关系，结合几何模型表述运算过程，运用乘法规则说明运算原理，最终通过综合运用推理方法确定哪个算式最接近6000。这样的教学旨在让学生在推理过程中有理有据，克服运算教学中的推理障碍，提升学生的整体思维能力。

（三）利用知识结构化培养推理意识

知识贵在求联，技能贵在求变，思想贵在求通。培养推理意识旨在体现运算的一致性，进而促进学生实现结构化学习。三位数乘以两位数的笔算是整数乘法最后的环节，笔者通过提问“为何学习了三位数乘以两位数后不再学习其他整数乘法？”引导学生利用竖式模型类比推理出多位数乘法的算法及原理，从而消除乘法运算间的障碍。学生在比较和整理中发现，乘法运算本质上是计数单位的累积过程，这有助于他们理解乘法的意义，并为学习小数、分数乘法打下基础。

本课分三个环节展开，各环节相互促进、相得益彰：始于三算、忠于模型、归于结构。通过揭示整数乘法的算理和算法，利用几何模型实现了从运算内容到运算思维的结构化突破，不断推进学生推理意识的进阶培养。

总之，运算能力是推理意识的前提，而推理意识的培养又能提升运算能力，二者相互依存，相辅相成，教学时不能顾此失彼。

（责编 金 铃）