小题串促生成，跨学科核心素养重培养

发展学生抽象能力和跨学科能力是培养学生核心素养的主要任务之一。本文以一节“反比例函数”的概念课为例，通过独到的一系列情境问题串或小题组，让学生在归纳概念、解决问题的同时，提升抽象能力；从身边的物理现象开始，培养他们跨学科解决问题的能力。

一、教学背景

我们都知道数学来源于生活，也应用于生活，而数学概念的学习是一个由具体到抽象的过程。学好数学概念有助于学生对知识的理解，发展学生的抽象思维能力。教师可以将知识应用于其他学科，或现实生活中，让学生用数学的方法去主动发现、提出、分析、解决现实生活中的问题。

以一节“反比例函数”的概念教学为案例。以一系列贴近学生生活的情境问题串或小题组的形式展示生活中的变化的量，促进学生思考，使学生通过这些情境中的具体数量关系，以及与一次函数、正比例函数的表达式的对比，抽象出反比例函数的概念。再通过一系列的小题组练习加深对反比例函数概念本质的进一步理解。最后通过一些跨学科的小题组应用练习，感悟概念内涵的同时，进一步加强学生跨学科核心素养的培养。

二、设计流程及设计说明

（一）展示课题及教学目标

课题：反比例函数

教学目标：

1.理解并掌握反比例函数的意义及概念。

2.会判断一个函数是不是反比例函数。

3.会求反比例函数的表达式。

（设计意图：板书课题，展示教学目标，让学生对本节的学习要求有整体的了解和预知。）

（二）填空小问题，回忆旧知识

问题1：一般地，在一个变化过程中，如果有两个

x和y，并且对于x的每个确定的值，y都有相应的值与其对应，那么我们就说 是 的函数，其中 是自变量。

问题2：形如 的函数是正比例函数。

形如 的函数是一次函数。

（设计意图：展示两个简单的填空串，一个是函数概念知识的填空，一个是正比例函数与一次函数的一般形式，学生容易将一次函数的一般形式中的k，b的取值忽略。所以，以填空问题串的形式回顾函数、一次函数及正比例函数知识，让学生在回忆旧知识的同时为本节课反比例函数的学习做铺垫。）

（三）情境小题串，对比抽象引概念

情境1：为了学好英语，小琳同学打算每天背10个英语单词，那么小琳所掌握的单词总量y（个）与时间x（天）之间的关系式是什么？（生：y=10x）

情境2：小琳同学原来已经记住110个单词，以后每天背10个单词，那么他所掌握的单词总量y（个）与时间x（天）之间的关系式是什么？（生：y=10x+110）

情境3：九年级英语全册大约有新单词1500个，小琳同学打算用x（天）全部背完，平均每天需要记忆的单词量y（个）与打算的时间x（天）之间的关系式是什么？（生：y=■）

情境4：已知银川市的总面积约9025 km2，人均占有面积s（km2/n）随全市总人口n（单位：人）的变化而变化，请写出s与n之间的关系式。（生：s=■）

情境5：京沪高速铁路全长约1318 km，列车沿铁路从上海驶往北京，列车行完全程所需要的时间t（h）与行驶的平均速度v（km/h）之间的变化关系式是什么？（生：t=■）

师：观察情境3、情境4、情境5的关系式，它们与情境1、情境2有什么不同之处？

生1：前两个是我们学过的一次函数和正比例函数，而后面三个明显与前面的不一样，都是一个常数除以一个变量。

生2：从关系上来看，前两个是一次函数和正比例函数，而后面三个是另外的一种。

生3：情境3中，如果小明打算30天背完，那么他平均每天要背50个单词；如果打算50天背完，那平均每天要背30个单词；如果打算60天背完，那平均每天要背25个单词，以此类推，y随着x的增加而减少，明显与前两个不同。一次函数和正比例函数，它们是y随着x的增大而增大。

生4：后面三个明显是同一类函数，它们总是可以写成一个变量等于一个常数除以另一个变量的形式。如果我们用x，y分别表示两个变量，用一个字母k表示常量，那么上面的形式就可以写成y=■（k为常数，且k≠0）。

师：这位学生说得非常清晰、明朗。如果两个变量x，y之间的对应关系可以表示为y=■（k为常数，且k≠0）的形式，那么我们就称y是x的反比例函数。反比例函数的自变量x不能为零。

（设计意图：呈现5个简单的情境小题串，它们既有联系，又有区别。前两个简单，学生可以轻松口述表达。后面三个则明显与前面两个函数不同，学生有明显的对比思考。通过对比感悟，学生强烈地感觉到后三个表达式与前面的不同，在对比中思考、感悟……学生的心里会逐步生成新的思维：从后面这三个关系式的特征来看，它们肯定是一种新的表达式，一种新的函数。

运用简单、贴近生活的情境小题串，调动学生的学习自信心、积极性，再通过潜移默化的对比分析，逐步生成学生想要的知识，从而抽象出反比例函数概念。在这一过程中，学生的思维开始从具体思维向形象思维转化。同时，这一过程既促进了学生知识点的生成，又发展并提升了学生的抽象能力，从而形成函数模型。）

（四）练习小题串，抽象概念深理解

导语：认识反比例函数以后，我们就把形如y=■（k为常数，k≠0）的这种函数都叫作反比例函数。接下来，就让我们来做个判断小练习。

练习1：下列函数中，x均为自变量，那么哪些y是x的反比例函数？k值是多少？

①y=-■ ②xy=■ ③■=1

④y=5x-1 ⑤y=■ ⑥y=■-1

⑦y=■

生5：①②④为反比例函数，k分别为-2，■，5。其中④可以写成y=■。

生6：（补充前面同学）第③个经过变形就写成了y=3x，所以它不是；第④个中，y=5x-1=5■=■，所以是反比例函数。

生7：第⑤中，虽然看起来与y=■很像，但是它的自变量的位置是（x+2），那也就是说自变量变成了（x+2），而题目中自变量是x，所以不是。第⑥⑦显然也不是。

师：从上面的判断来看，反比例函数还可以写成xy=k（k≠0），y=kx-1（k≠0）的形式。

练习2：①若y=■是反比例函数，则m应满足的条件是 。

生8：m≠-1。

②若y=（m+1）xm2-2是关于x的反比例函数，确定m的值，并求其函数关系式。

生8：由题可知：m+1≠0，且m2-2=-1。

得：m=1。

所以，该反比例函数的关系式为：y=■。

练习3：y是x的反比例函数，表1给出了x与y的一些值。

（1）写出这个反比例函数的表达式。

（2）根据函数表达式完成表1。

师：如何求反比例函数表达式？你认为要求表达式关键是求什么？

生9：求函数表达式的关键是求出k的值。

生10：设反比例函数表达式为y=■（k≠0），把x=-1，y=2代入表达式，得：k=-2，所以，反比例函数的表达式为y=■。

生11：因为题目中说是反比例函数，所以我们设反比例的函数表达式为y=■（k为常数，且k≠0），我们发现表格中有一对x，y的值，就把这对数值代入函数表达式，得到k=-2。所以得出反比例函数的表达式为y=■。

生12：根据前面同学求出的反比例函数表达式，我们可以求出表1中的其他值依次为：-3，1，2。

生13：从上面的计算过程，我们发现求函数表达式的过程实际就是求系数k的值。这个过程可以是：先设反比例函数表达式；然后把一组对应的x，y的值带入；接着求出系数k的值；最后写出函数表达式。

设计说明：前两个问题的重点在于强化学生对反比例函数的概念本质的理解，让学生深刻体会反比例函数中变量x，y与常数k之间的关系，并发现反比例函数的其他书写形式。在此基础上，进一步明确第三个问题：确定一个反比例函数关系式的关键是求非零常数k的值。同时，让学生初步体会函数表达式与函数表格这两种形式的相互转化，在这里多让学生说说他们的做法、见解，从而增强学生探索学习的自信心，获得自我价值感。

在教学中，我们常常需要一些练习小题串来帮助学生理解知识点、概念、性质、运算规则等。这就需要教师精心设计这些练习小题串。这些小题串可以是同类型的不同表达方式型的；也可以是由易到难地逐步提升型的；还可以是不同类的对比型的；还可以是由具体实物生成符号的抽象型的。总之，通过小题串的练习，学生加强了对知识点本质的理解感悟，能在万千变化的问题中确定性质的特有属性。

（五）跨学科小题串，抽象思维重培养

过渡：在生活中，反比例函数的应用极其广泛，也会出现在其他学科中，让我们来看看物理学中的反比例函数。

教师举例：有这样一种台灯，随着开关旋钮的转动，我们会发现台灯越来越亮，这是什么原因呢？原来，随着旋钮的转动，台灯的电阻越来越小，电流就会越来越大。比如下面这个问题。

设计说明：关于电流、电压、电阻的物理问题在初中生的认知里是比较抽象的，学生理解起来比较困难。为了避免学生理解上出现卡顿，在展示下面的问题1之前，教师先举出生活中的渐变式台灯。由渐变式台灯，学生可以浮想联翩：广播、音响、耳机声音的大小变化等。这样，既贴近生活，又牵引到了物理学科知识。从而让学生进一步体会、理解反比例函数中x、y变化的关系。

问题1：电流I，电阻R，电压U之间满足关系式U=IR。在照明电路中，正常电压U=220伏。

（1）求I与R之间的函数关系式。

（2）变量I是R的反比例函数吗？

（3）利用写出的关系式，完成表2。

生15：I与R之间的函数关系式为：I=■。I是R的反比例函数。

（设计意图：教师结合生活中的实例现象，引导学生解决有关电流、电阻、电压之间的关系的问题。使学生从具体的实物到物理学科中抽象的电问题，体会物理中的电阻、电流间的变化关系，再对比概念中y与x间的变化关系，从而抽象出反比例函数模型，进一步巩固学生对反比例函数意义的理解，从而抓住概念本质。同时，也培养了学生跨学科的抽象思维意识及跨学科的应用意识。）

问题2：在某一电路中，保持电压U（伏）不变，电流I（安）是电阻R（欧）的反比例函数，当电阻R=3欧时，电流I=4安。

（1）求I与R之间的函数关系式。

（2）当电流I=0.6安时，求电阻R的值。

生16：（1）因为I是R的反比例函数，所以I=■。

把R=3，I=4代入关系式，得：U=12，所以I与R之间的关系式为：I=■。

（2）当I=0.6时，R=200（欧）。

设计说明：还是电流、电阻、电压的问题，有了上一个问题的铺垫，学生很轻松地感觉到电流、电压、电阻之间的关系就是反比例关系。问题2在上面问题的基础上，增加了难度，让学生经历在抽象的物理问题中求反比例函数关系式。从其他学科的角度来理解数学概念的本质特性。让学生会用数学的眼光去发现、观察这一物理现象；会用数学的思维去思考这一物理问题；并用数学的语言表达电阻、电流间的反比例关系。

师：通过上述的解答过程，你能说说如何求反比例函数的表达式吗？

生17：用待定系数法，也就是①设函数表达式；②代入一组x、y的值；③求出系数k的值；④写出函数表达式。

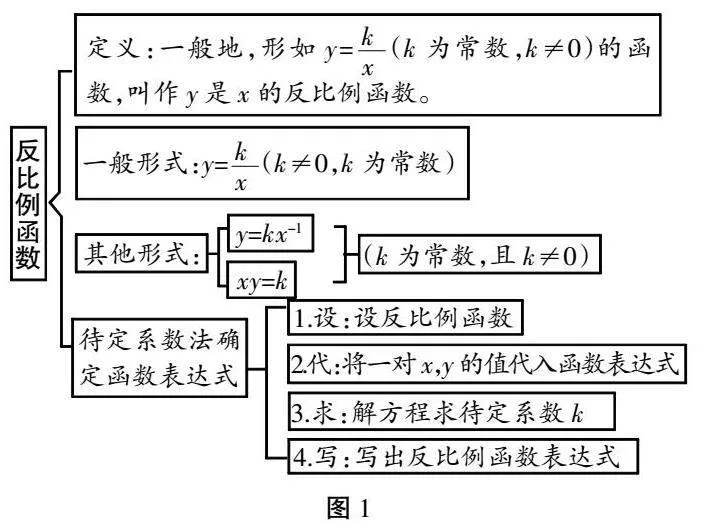
（三）归纳总结（展示思维导图，见文末图1）

（设计意图：以思维导图的形式，对本节课的知识进行梳理，让学生在归纳总结中抽象本节课的知识要点，进一步培养学生的抽象意识。）

三、总结

本节课以小题串或小题组的形式穿针引线，抽象出反比例函数概念，抽丝剥茧出反比例函数概念的深度内涵，再以生活现象牵引出物理中的数学。最后运用数学概念、原理及方法等来解释物理学科方面的现象特征。虽然是一节简单的反比例函数的概念课，却让学生经历了从现实问题情境中抽象出反比例函数概念的抽象思维过程，并将这一抽象的数学模型应用于抽象的物理学科中，让学生在解决问题的过程中，感悟数学函数模型的通性，从而达到学以致用的效果。

简单的小问题串、小情境串、小题组蕴含了大大的能量。小小的问题串，可以让学生发现问题、寻找策略、生成知识内涵，从而信心满满地解答问题。在解决问题的过程中，学生通过实践、探究、体验、反思、分析、交流等过程，积累数学活动经验，体会数学知识之间、数学与其他学科之间及生活实践之间的关联。

数学是认识、理解与表达现实世界的一种基本方式，跨学科的应用对数学知识的理解、技能的巩固、思想方法的感悟都是至关重要的。因此，在教学中，我们要积极培养学生的跨学科应用意识，从而激发学生的数学学习兴趣与热情，促使他们去自主地探究数学。掌握了数学知识属性、概念特性等，学生就更愿意从数学角度去参与跨学科综合实践活动，感悟数学与现实世界的联系，进而解决更多实际活动中存在的问题。

（作者单位：银川市唐徕中学宝湖校区）

编辑：曾彦慧