基于任务情境的初中数学教学设计与实施

以任务情境为特征的教学，强调创设贴近学生生活实际、富有挑战性的问题情境，引导学生在解决问题的过程中实现知识和技能的习得、过程和方法的体验以及情感态度与价值观的形成。本文基于任务情境理念，以初中数学“圆与正多边形”为例，探索教学活动的设计与实施策略，为学生数学核心素养的培养提供参考。

一、教学目标

1.数学语言的建构与运用：能够描述圆与正多边形的关系，解释设计方案，并论证自己的计算过程；培养逻辑连贯的表达能力和数学交流能力。

2.数学思维的发展与提升：培养观察、猜想和论证的能力，发展批判性思维和创造性思维。

3.审美鉴赏与创造：理解对称性和比例在设计中的重要性；培养设计思维和审美能力，增强学生的空间想象力，培养将数学美感应用于实际创作的能力。

二、教学过程

（一）导入：创设任务情境

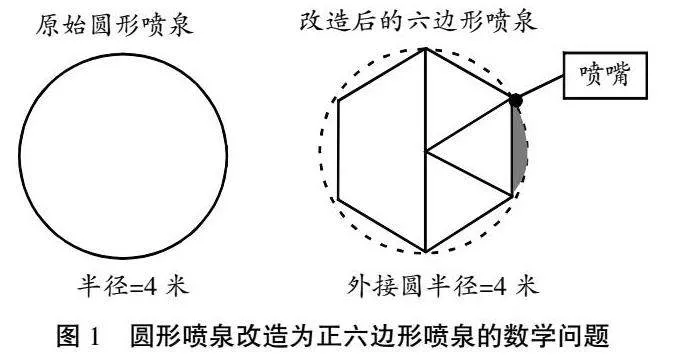
教师展示城市广场航拍图，中央有大型圆形喷泉，并介绍市政府计划将喷泉改造成正六边形，以提升美观度和实用性。新喷泉保持原规模，外接圆半径4米。教师提出三个问题：确定六边形边长，使其内接原圆；计算改造后喷泉的周长和水面面积。（强调：这些计算对材料采购和水泵设计很重要。）接着介绍创新设计：在六边形每个顶点安装喷嘴，形成扇形水流。教师在黑板上画单位圆（半径为1）和内接正六边形，指出每个喷嘴水流形成60°扇形（见图1）。提出三个进阶问题：扇形总数、每个扇形面积、扇形覆盖区与六边形水面的面积差（即阴影部分）。这些问题综合运用圆与正多边形的知识，将抽象数学知识应用于实际工程设计。

（二）新知探究：正多边形的性质

教师引导学生观察六边形喷泉模型，提问：“喷泉的每个边看起来一样长，这告诉我们什么？”学生讨论后得出正多边形边长相等的特征。教师再问：“喷泉中心到每个顶点的距离相等吗？”学生测量后发现都是4米，引出正多边形外接圆半径的概念。

教师在模型上标出中心到边的连线，问：“这些线段有什么特点？”学生观察后发现它们等长且平分边，引出正多边形的半径和边心距概念。教师提示：“如果知道半径，如何求边长？”学生尝试后，教师引导得出边长等于半径的结论。

针对喷泉的周长计算，学生提出6乘以边长的方法。教师肯定后，引导学生推广到n边形，得出周长公式：C=na。关于面积，教师建议将六边形分割成六个三角形，学生计算后得出面积公式：

S=■na2sin（■）。

（三）例题讲解：正六边形的周长和面积

教师回顾喷泉设计任务：“我们现在需要计算新六边形喷泉的周长和面积。设计图显示外接圆半径为4米，让我们一步步解决这个问题。”

首先，教师引导学生回想之前结论：“正六边形的边长等于外接圆的半径，所以喷泉每条边长是多少？”学生很快得出4米的答案。教师继续：“知道边长后，如何计算周长？”学生提出6乘以4的方法，得出周长为24米。教师借机引入通用公式：C=6a，其中a为边长。

其次，教师转向面积计算：“计算水面面积更复杂，我们可以把六边形分成六个等边三角形。”教师在黑板上绘制了一个等边三角形，标出高线。“这个三角形的底是多少？高怎么算？”引导学生发现高等于2■。“现在我们可以计算一个三角形的面积了，然后乘以6。”

学生计算得出一个三角形面积为4■，总面积为24■。教师总结：“我们可以写成S=6×（■×4×2■）=24■。”

最后，教师将问题拓展到实际应用：“知道周长和面积后，我们可以计算铺设地砖的数量和所需水量。假设地砖宽度为0.5米，宽度为0.1米，你们能计算出需要多少块地砖吗？如果水深为0.5米，喷泉需要多少立方米的水？”

（四）练习与巩固

教师引入新的挑战：“市政府对我们的六边形喷泉设计很满意，现在他们想探索更多方案。让我们一起设计不同形状的喷泉。”

教师呈现圆形喷泉改造任务：“将喷泉改造成正八边形，保持原来4米的外接圆半径，如何计算新喷泉的周长和面积？”学生分组讨论，运用C=na和公式S=■na2sin（■）进行计算。教师巡视指导，关注学生对公式的理解和应用。计算完成后，教师提出实际应用问题：“设计师提议在喷泉周围安装LED灯带，每米需要10个LED灯，每个灯2元。正八边形喷泉需要多少个LED灯？总成本是多少？”学生需要将周长计算与成本估算结合，深化对数学应用的理解。

接着，教师引入水资源管理问题：“假设正八边形喷泉的水深为0.6米，请计算所需水量。与之前的六边形喷泉相比，哪个更节水？”这个问题要求学生计算体积并进行比较分析，将面积计算扩展到实际应用层面。为了拓展学生思维，教师提出开放性问题：“如果继续增加喷泉的边数，趋近于圆形，其周长和面积会如何变化？”教师借此引导学生探讨极限情况，加深对圆与正多边形关系的理解。

在整个练习过程中，教师鼓励学生讨论，分享不同的解题策略。各组完成后展示设计方案和计算结果。教师适时点评，强调数学模型在实际工程中的应用价值，如成本估算、资源管理等。

（五）拓展探究：圆内接正多边形

教师展示新的喷泉设计图：“市政府提出了一个创新想法，在圆形水池边缘安装多个喷嘴，形成多边形喷泉效果。我们来探讨这个设计。”

教师在黑板上绘制一个单位圆，标出圆心O和圆周上的点A、B。连接OA、OB形成圆心角AOB，再连接AB形成内接线段。“假设圆心角AOB为60°，AB就是内接正六边形的一条边。”

学生观察图形，教师引导：“圆心角和内接正多边形边数有什么关系？”学生讨论后得出：边数n=■。“那么，60°对应几边形？”学生很快回答：“正六边形。”教师继续：“现在，我们来计算这个喷泉的实际尺寸。假设水池半径为1米，求内接正六边形的边长和面积。”学生运用三角函数，推导出边长a=2sin（■），此处n=6。

计算完边长后，教师引导学生思考面积：“我们把六边形分成六个等腰三角形。”学生计算三角形面积，然后乘以6，得出六边形面积公式：

S=（■）cot（■）。

教师提出实际问题：“如果我们在每个顶点安装喷嘴，喷出60°的扇形水流，覆盖面积如何计算？”学生运用扇形面积公式■，计算单个扇形面积，再乘以6。比较一下六边形面积和扇形覆盖面积，哪个大？差多少？学生进行计算和比较，发现扇形覆盖面积大于六边形面积，差值即为水流覆盖的额外区域。

教师鼓励学生思考：“如果增加喷嘴数量，内接多边形和扇形覆盖面积会如何变化？这对喷泉设计有什么启示？”学生讨论不同边数对水流覆盖效果的影响，体会数学知识在实际设计中的应用。

（六）总结与反思

教师引导学生回顾通过喷泉设计项目学习的关键数学概念和公式。学生重温正多边形的定义、内角和、中心角等基本概念以及周长公式和面积公式。通过回顾计算喷泉边长、周长、面积的过程，以及LED灯带设计和水资源管理等应用案例，学生深刻认识到了数学知识在实际工程中的重要性。教师还引导学生思考了圆与正多边形之间的关系，特别是边数增加时多边形逐渐接近圆的过程，加深了学生对极限概念的理解。学生分享了对这种基于实际项目学习方式的体会，普遍认为将抽象数学概念应用到具体工程问题中很有价值。最后，教师总结。通过喷泉设计，学生不仅掌握了计算公式，更重要的是理解了数学知识在现实世界中的应用。希望这次经历能激发他们继续探索数学与工程之间的联系。

三、任务情境下教学的意义

（一）促进知识的整合与应用

任务情境下的教学，将知识点有机融入具体情境，为学生提供了综合运Qlg1Yq8iQmc12UdrDPi165IEWRoCJ2/7X8lKzpvn92c=用知识的机会。以圆与正多边形为例，学生在解决亭子地基设计问题的过程中，需要综合运用圆的周长、面积公式，正多边形的特征、性质等知识，将零散的知识点整合为解决实际问题的工具。这种学习方式不仅加深了学生对知识的理解，更促进了知识的迁移与应用。通过设计任务情境，学生能够感受到数学与生活的紧密联系，提高学习数学的兴趣和主动性。在解决问题的过程中，学生的逻辑思维、空间想象等能力得以提升，为今后学习更复杂的数学知识奠定了基础。

（二）培养学生的数学核心素养

数学核心素养是学生适应个人生活和未来发展需要所必备的数学品质和关键能力。任务情境下的教学，为培养学生的数学核心素养提供了良好的平台。在设计亭子地基的任务中，学生需要运用数学抽象、逻辑推理等数学思维方法，分析问题、构建模型、论证结论，体现了数学抽象、逻辑推理等核心素养。同时，学生在合作探究中，通过交流、讨论、评价等方式，提高了数学表达与交流的能力。在探索问题解决策略的过程中，学生运用多种数学工具和资源，体现了数学建模和数学运用的素养。任务情境为学生提供了展示创新意识和批判性思维的机会，培养了学生的创新意识和创新能力。

（三）提高教师的教学设计能力

任务情境下的教学，对教师的教学设计能力提出了更高的要求。教师需要根据教学内容和学生特点精心创设任务情境，把握任务的难度和开放程度，引导学生在探究中获得知识和能力的提升。在设计亭子地基的教学中，教师需要有机整合圆与正多边形的知识点，创设合适的问题情境，预设学生可能遇到的困难和解决策略，提供适当的支架和指导。这一过程不仅考验教师的数学专业知识，更考验教师的教学智慧和设计能力。通过不断的实践与反思，教师可以优化教学设计，提高教学质量。教师通过集体备课、教学研讨等方式，与同行交流教学设计经验，共同提高教学设计能力。

基于任务情境的数学教学为培养学生的核心素养开辟了新途径。通过设计喷泉这一贴近生活的项目，本文展示了如何将抽象的数学概念与具体的工程实践相结合的方法。这种教学方法不仅促进了知识的整合与应用，还培养了学生的问题解决能力、创新思维和团队协作精神。教师在设计过程中需要精心构建情境，把握难度，为学生提供适当的引导和支持。这种教学模式对教师的专业素养提出了更高要求，同时为教学创新提供了广阔空间。

（作者单位：江苏省宿迁经济技术开发区南蔡实验学校）

编辑：常超波

作者简介：郑新涛（1984—），男，汉族，江苏宿迁人，本科，中小学一级教师，研究方向：初中数学教育教学。