翻转课堂在高中数学教学中的应用探析

【摘要】翻转课堂作为一种新颖的教学手段，在高中数学教学中合理运用可增强学生的学习驱动力，保证学生的学习效率．特别对于复杂难懂的数学知识，翻转课堂的有效利用，能够发挥良好的教育作用．本文围绕向量教学，探索翻转课堂在高中数学教学中的运用对策，希望为高中数学教师提供向量教学新思路．

【关键词】翻转课堂；高中数学；课堂教学

在高中数学教学组织中，翻转课堂的合理应用，有良好的实用性特点，但是由于翻转课堂是一种新颖的教学方式，教师缺少丰富的应用经验，使其整体教学效果差强人意．想要充分展现翻转课堂的教育作用，还要根据高中数学学科的基本特点，将学生的学习基础、接受能力作为翻转课堂的落脚点，总结概括翻转课堂的教学经验，使翻转课堂的教育作用充分展现出来，促进学生全面发展．

1 有关向量的知识点分析

在高中数学教学中，向量知识点占据主导地位，也是高考数学试卷中常见的考点之一．在分析高中数学向量习题过程中，学生要触及众多数学知识，还要掌握向量几何和物理的要点．为此，对于高中学生来讲，向量知识点既为重点，亦为难点．在高中数学向量教学组织中，教师想要达到预期目标，应从学生日常生活入手，为学生构建真实的生活情境^［1］，使学生在熟知的生活情境中思考问题，加深学生对向量知识点的理解．然而，高中数学教师若只是习惯运用常规“教师教+学生学”的固定方式，学生对于此部分的知识理解往往会停留于表面，还会限制学生学习能力、应用能力的发展，这就要求高中数学教师探索新颖的教学手段，激发学生的学习驱动力，使学生克服向量学习难点，提高向量教学质量．

2 翻转课堂的特点概括

2.1 科学合理

高中数学教师在教学组织中，想要运用翻转课堂教学方式，需要明确整体教学目标^［2］，以便根据教学目标，进行教学内容、教学环节的设计．例如，在课堂教学前8～15分钟左右，教师要适时导入新知识，为学生讲授重点内容，以免由于学生学习疲劳、兴趣低下而出现注意力不集中的情况，影响整体教学效率．

2.2 教师与学生角色互换

在高中数学翻转课堂中，强调学生是学习的主人，教师要发挥引导促进作用，扮演好教学组织者的角色，控制好教学的大方向与教学进程，根据学生的课堂表现、学习基础、接受能力等^［3］，运用适合学生的学习方式，增强学生的学习驱动力，改变常规“教师教+学生学”，即教师一讲到底的教学模式.学生长期处在被动学习地位，容易对教师形成过度依赖，出现不善思考、甚少发言的教学情况，影响整体教学质量．

2.3 丰富多彩

相较于常规教学方式，翻转课堂教学方式、教学工具更加灵活，为高中数学教师提供多重选择．在此种情况下，高中数学教师要根据学生的学习差异性、学习基础、发展要求，选取适当的教学方式^［4］，不断调整教学内容、教学目标、教学进程，为课堂教学注入新鲜元素，才能让学生对所学内容产生浓厚兴趣，保持良好的学习状态，提高学生学习效率，发挥翻转课堂的教学作用．

3 在高中数学教学中翻转课堂教学的运用对策

3.1 注重学情分析

纵观历年的高考数学试卷，可以发现向量作为必考考点，占据一定的分值，且向量知识有显著的理论性、综合性特点^［5］.

例如 向量基础运算，不但涉及高中数学知识与几何知识，还包括高中物理知识与力学知识．为此，高中数学教师想要提高整体教学水平，应在教学准备期间，做好教学难点、教学重点的分析工作，为学生精心设计引导作用显著的教学目标、教学方案，保障各项教学环节有序展开．具体为：是否要巩固复习和向量有关的旧知识，通过哪种方式进行向量教学导入，是否要制作向量教学课件，明确向量教学组织中的相关影响因素，制定行之有效的应对对策，了解向量教学中的注意要点等．只有高中数学教师做好以上准备工作，才能把握教学主线，促进教学目标的实现．

3.2 注重教学环节

高中数学教师在向量教学中，运用翻转课堂教学方式，旨在引导学生复习与向量相关的知识要点，涵盖向量、零向量、平行向量以及相反向量等概念，从而增强学生的学习驱动力，使学生保持良好的听课状态^［6］，以便进入新知识的讲授之中．

3.3 注重例题引用

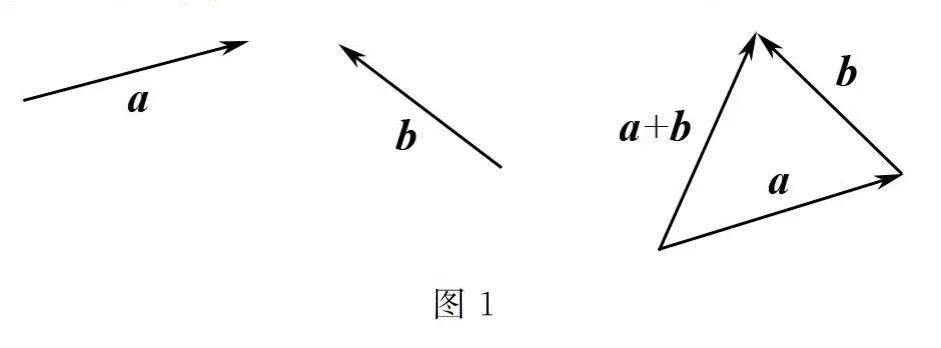
例1 在动态化视频中，向学生呈现“假期小明与父母出去旅游”的情境．小明与父母的旅行路线始于北京，途经青岛，最终抵达菏泽．请同学们深入思考，假如直接从北京前往菏泽，这两个位置会发生怎样的变化？它们之间有哪些关系？学生看完动态化视频后，在电子白板大屏幕中呈现不同的图形（如图1所示），在图中已经知晓ɑ与b的向量，求证ɑ+b．

学生根据动态化演示与亲自画图，分析出：两个向量的和为一个向量，这是向量加法的基本性质．基于此性质，学生可以推导出向量加法的三角形法则：将两个向量首尾相接，从起点到终点的连线即为这两个向量的和．

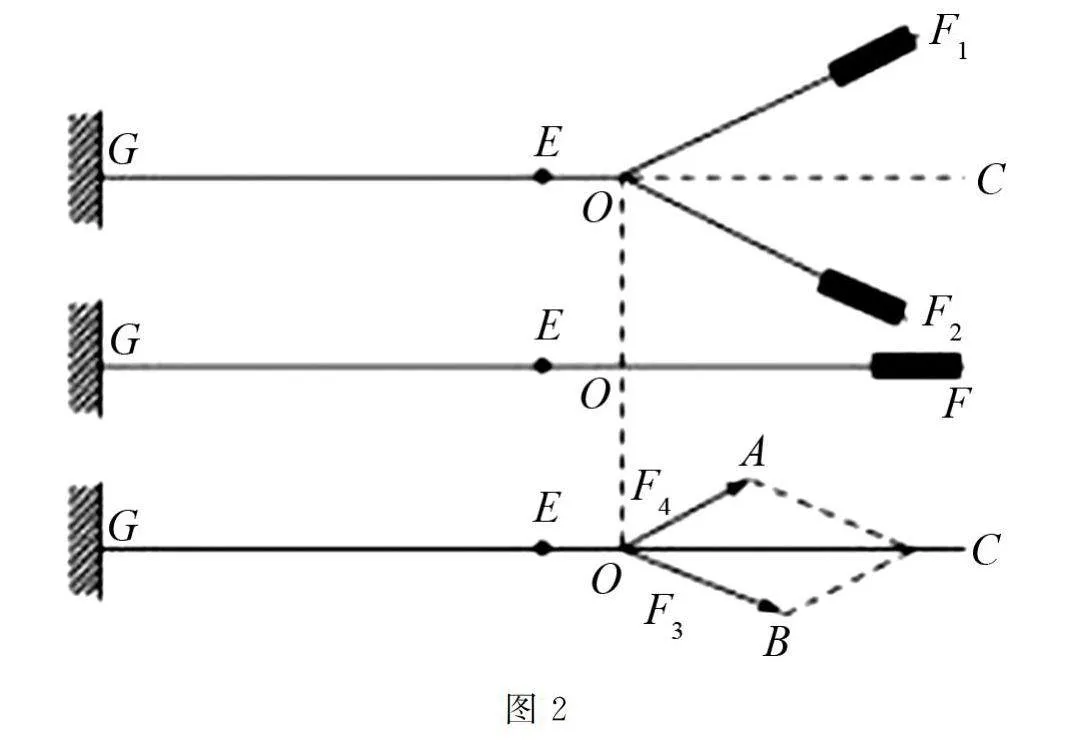
例2 审阅图2，可知在力F和F的相互影响下，弹簧沿着直线GC方向，使EO线段长度呈现明显改变化．将力F和F消除后，向其施加力F，将弹簧拉伸至点O部位．你们可以把这两次力的大小准确标注出来吗？同时分析力的方向，此时学生进行图像观察，发现向量加法呈现为平行四边形形态．

学生在翻转课堂中，对于问题与已知条件展开深层分析，依照向量加法的平行四边形法则，将两个相同起点的向量视为平行四边形的邻边，将平行四边形画出来．把公共起点和对角线连接好，对角线上的向量即为两个向量的和向量．

例3 在图3中，可以看到河道两旁并未修建桥梁，因此只能借助渡轮，运输相应的货物，一艘渡轮在A点处出发，向着与河岸方向保持垂直的角度行驾．已知渡轮行驶速度保持每小时5千米，河流流速测量为向东每小时2千米．根据向量知识要点，说明水流的速度、渡轮行驶速度、渡轮在精准导航情况下的速度、渡轮驾驶方向等．

教师让学生基于向量的层面：假设a和b属于同向的情况下，表明a+b的方向与a和b的方向一致；假设向量a和b属于反向的情况下，表明a+b的方向将与a和b中数值较大的那个向量的方向保持一致．

教师让学生利用自身掌握的向量知识点，梳理相应的解题思路，找到解决问题的诀窍：在a与向量b的方向处于相同情况下，表明a+b的指向与a、b指向相统一；而在a和向量b指向存在差异的情况下，表明a+b的指向要进一步分析数值更大的向量．

在a+b≤a+b向量不等式中，唯有a与b的方向保持一致时，等量关系方可成立；对于a+b≥a－b向量不等式中，a与b的方向存在明显差异，才能满足等量关系．

因教师习惯在课后为学生导入练习题，高中数学教师要在翻转课堂中，向学生抛出典型的与向量知识相关习题，达到融会贯通、学以致用的效果．

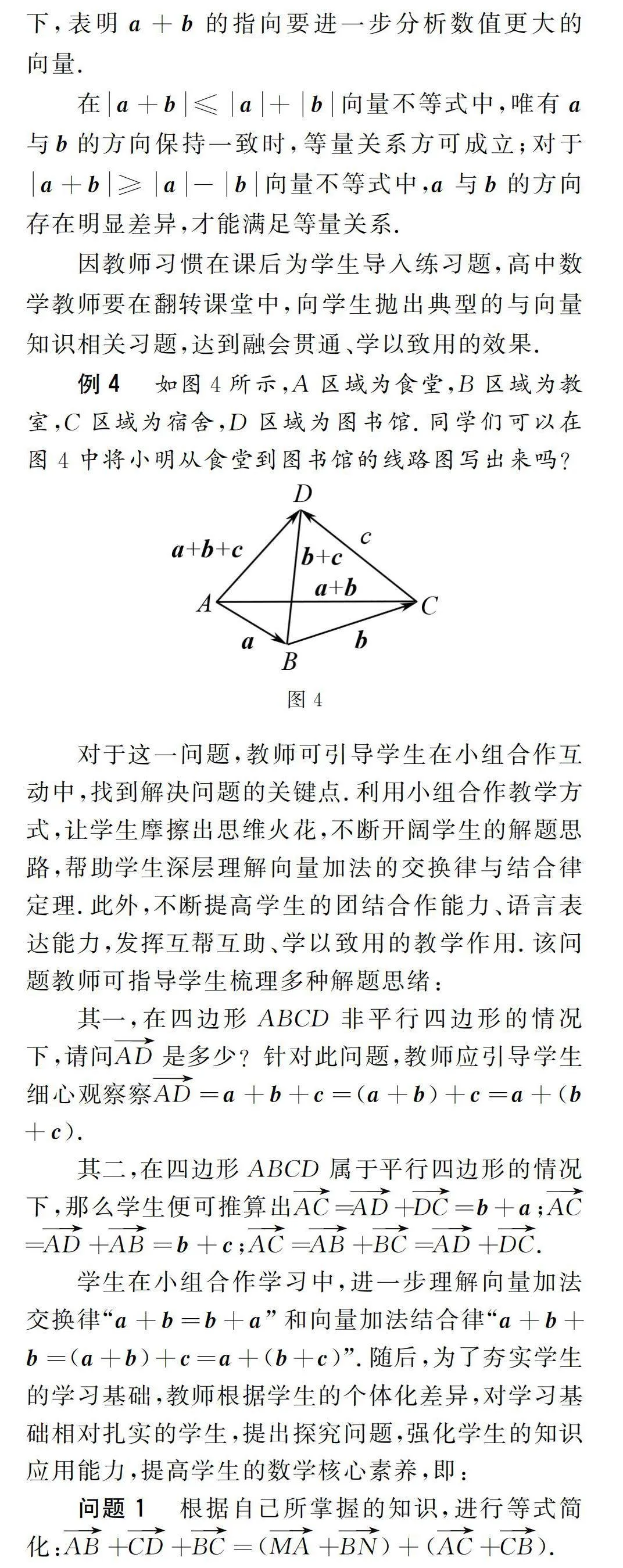
例4 如图4所示，A区域为食堂，B区域为教室，C区域为宿舍，D区域为图书馆．同学们可以在图4中将小明从食堂到图书馆的线路图写出来吗？

对于这一问题，教师可引导学生在小组合作互动中，找到解决问题的关键点．利用小组合作教学方式，让学生摩擦出思维火花，不断开阔学生的解题思路，帮助学生深层理解向量加法的交换律与结合律定理．此外，不断提高学生的团结合作能力、语言表达能力，发挥互帮互助、学以致用的教学作用．该问题教师可指导学生梳理多种解题思绪：

其一，在四边形ABCD非平行四边形的情况下，请问AD是多少？针对此问题，教师应引导学生细心观察察AD=a+b+c=（a+b）+c=a+（b+c）．

其二，在四边形ABCD属于平行四边形的情况下，那么学生便可推算出AC=AD+DC=b+a；AC=AD+AB=b+c；AC=AB+BC=AD+DC．

学生在小组合作学习中，进一步理解向量加法交换律“ɑ+b=b+ɑ”和向量加法结合律“ɑ+b+b=（ɑ+b）+c=ɑ+（b+c）”．随后，为了夯实学生的学习基础，教师根据学生的个体化差异，对学习基础相对扎实的学生，提出探究问题，强化学生的知识应用能力，提高学生的数学核心素养，即：

问题1 根据自己所掌握的知识，进行等式简化：AB+CD+BC=（MA+BN）+（AC+CB）．

问题2 已知一架飞机向南飞行500千米，又向西飞行400千米，你知道这架飞机的总飞行距离是多少千米吗？两次飞行的位移合成总共是多少千米？

3.4 注重教学总结

经过长时间的实践，翻转课堂会为学生建立完整的知识体系，使各项知识都能得到良好应用，提高学生的知识应用能力．通过帮助学生形成良好的做题习惯^［7］，不但能提高学生的解题能力，还能使学生端正自身的学习态度，形成良好的数学思维能力．

4 结语

综上所述，高中数学教师沿用常规教学方式，常常是持续灌输，甚少引导学生自主思考、主动质疑、大胆设想．长此以往，容易降低学生的学习驱动力，难以强化学生的数学逻辑思维能力，达不到核心素养培养的目的．为此，在新课程改革指导下，翻转课堂凭借科学的教育观念、有效的教学手段，代替常规的授课方式，推动教育教学创新发展．由于高中数学教学有显著的理论性、抽象性特点，运用翻转课堂，能够为学生构建活跃的教学环境，使抽象复杂的学科知识变得形象生动，降低学生的学习难度，激发学生的学习驱动力，使学生保持良好的学习状态参与到课堂学习之中，学生的学习效率、学习能力得到大幅度提高，有助于促进学生全面发展．

参考文献：

［1］白志荣.翻转课堂教学模式在高中数学教学中的实践策略研究——以向量的教学为例［J］.考试周刊，2021（99）：61-63.

［2］郁杰华.翻转课堂在高中数学教学中的实践应用［J］.数学大世界（上旬版），2021（04）：77.

［3］郑金萍.“翻转课堂”在高中数学教学中的应用［J］.数理化学习（教育理论），2021（03）：45-46.

［4］盛祥.翻转课堂在高中数学教学中的应用探析［J］.教育界，2021（46）：34-36.

［5］何睦.“数学思考”的教学：教什么、怎么教——以“平面向量的概念”一课的教学为例［J］.中国数学教育（高中版），2022（12）：18-22.

［6］邵曦.基于学习进阶的高中数学教学设计——以“平面向量的应用”为例［J］.中学数学（高中版），2022（02）：15-16.

［7］江潞潞.课堂实践中探索核心素养落地——以“平面向量基本定理”的教学为例［J］.数学教学通讯，2023（03）：31-33.