高中物理中变力做功问题的解题技巧

【摘要】在高中物理学习中，变力做功问题是一个常见的难点.本文旨在探讨解决变力做功问题的两种常用方法：微元法和平均值法.并结合具体例题进行讲解，帮助学生更好地理解和掌握这两种方法，提高他们解决变力做功问题的能力.

【关键词】高中物理；变力做功；解题技巧

1 引言

在高中物理学习中，变力做功问题是一个常见的难点.由于力的大小和方向可能随着位移的变化而变化，使得变力做功的计算变得复杂.为了解决这一问题，可以采用微元法和平均值法.本文将对这两种方法进行详细探讨，并通过具体例题进行讲解.

2 微元法求解变力做功

微元法在处理变力做功问题时，其核心思想是将整个位移区间分成无数微小的小段，每一小段内力的大小和方向近似不变，从而可以将其视为恒力.对于每一微小位移，力可以认为是恒定的，因此在该微小位移上做的功为力的值乘以位移的大小.接下来，对整个位移区间进行积分，将所有微小段上的功加起来，即可得到整个过程中变力做的总功.这种方法特别适用于力随位移连续变化的情况，如弹簧力、引力等，能够将复杂的变力做功问题转化为简单的积分问题，从而有效求解.

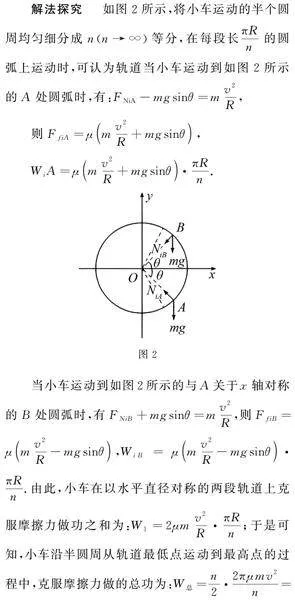
例1 如图1所示，质量为m的小车以恒定速率v沿半径为R的竖直圆轨道运动，已知小车与竖直圆轨道间的摩擦因数为μ，试求小车从轨道最低点运动到最高点的过程中，克服摩擦力做的功.

思路分析 小车沿竖直圆轨道从最低点匀速率运动到最高点的过程，由于轨道的支持力是变力，所以所受的摩擦力也是变力，不能根据功的公式求克服摩擦力做功，可用微元法求解.

解法探究 如图2所示，将小车运动的半个圆周均匀细分成nn→∞等分，在每段长πRn的圆弧上运动时，可认为轨道当小车运动到如图2所示的A处圆弧时，有：FNiA－mgsinθ=mv2R，

则FfiA=μmv2R+mgsinθ，

WiA=μmv2R+mgsinθ·πRn.

当小车运动到如图2所示的与A关于x轴对称的B处圆弧时，有FNiB+mgsinθ=mv2R，则FfiB=μmv2R－mgsinθ，WiB=μmv2R－mgsinθ·πRn.由此，小车在以水平直径对称的两段轨道上克服摩擦力做功之和为：W1=2μmv2R·πRn；于是可知，小车沿半圆周从轨道最低点运动到最高点的过程中，克服摩擦力做的总功为：W总=n2·2πμmv2n=πμmv2.

解决本题的关键要运用微元法求变力做功，要知道摩擦力是变力，不能直接根据功的公式计算其做功.

3 平均值法求解变力做功

平均力法不同于微元法.微元法是将整个位移区间分成无限多个无限小的微元，然后在每个微元内将变力视为恒力，而平均力法则是在整个位移区间内取一个平均力来计算总功，不需要将位移区间分成微元.平均力法在处理变力做功问题时，其核心思想是将整个过程中变力的大小和方向的变化近似地视为一种均匀变化.具体来说，当力随位移的变化呈现出某种规律时，则可以假设在整个位移区间内，力的大小和方向是均匀变化的.然后，利用这个平均力与整个位移区间的乘积来计算变力所做的功.由于假设了力是均匀变化的，因此这个平均力能够较好地反映整个过程中力的大小和方向的变化情况.需要注意的是，平均力法是一种近似方法，它只适用于力随位移均匀变化或变化不剧烈的情况.如果力的变化非常剧烈或没有规律，那么使用平均力法计算的结果可能会有较大的误差.

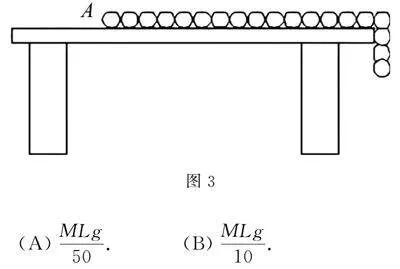
例2 如图3所示，有一根长为L，质量为M的均匀链条静止在光滑水平桌面上，其长度的15悬于桌边外，如果在链条的A端施加一个拉力使悬着的部分以0.1g（g为重力加速度）的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触，则拉力最少需做功（ ）

（A）MLg50. （B）MLg10.

（C）MLg250. （D）MLg25.

思路分析 假设链条悬着的部分被拉回x时，拉力为F，根据牛顿第二定律求出F与x的关系，可知F与x是线性关系，再求F的平均值，由F的平均值与位移的乘积求F做的功.

解法探究 设链条悬着的部分被拉回x时，拉力为F，对整个链条，根据牛顿第二定律得：F－15L－xLMg=M·0.1g，可得F=0.3Mg－xLMg.

则刚开始拉链条时，x=0，F1=0.3Mg，链条全部拉回桌面的瞬间，x=15L，代入F=0.3Mg－xLMg得F2=0.1Mg，所以F的平均值为F=F1+F22=0.2Mg，拉力最少需做功W=FL5=MgL25，故选（D）.

本题中拉力是变力，必须根据拉力的平均值求拉力做功，根据牛顿第二定律得到拉力与位移的关系是关键.

4 结语

本文通过对微元法和平均值法的原理、适用条件、解题步骤进行详细分析，并结合具体例题进行讲解，帮助学生更好地理解和掌握这两种方法，提高解决变力做功问题的能力.在实际解题过程中，学生应根据具体情况选择合适的方法，以达到简化计算、提高解题准确率的目的.

参考文献：

[1]南从从.探究高中物理中求变力做功的方法[J].数理化解题研究，2023（24）：68-70.

[2]王慧娟.基于核心素养理念的高中物理概念教学研究[D].扬州大学，2022.

[3]刘育昂.浅析高中物理变力做功问题[J].中外企业家，2018（23）：184.