高中物理动态平衡问题的处理之相似三角形法

【摘要】在力的平衡知识点中，传统“旋转法”在处理某些情况下力的变化问题时具有局限性.本文针对高中物理动态平衡问题，提出基于相似三角形的解题方法.该方法能够通过寻找力的三角形和几何三角形之间的相似关系，直观地判断力的大小变化情况.本文详细介绍了该方法的五个步骤，并通过实际例题验证该方法在解决高中物理力学问题中的实用性和有效性.

【关键词】高中物理；动态平衡；解题方法

1 引言

高中物理力学题目众多，某些题目需要在受力的动态平衡中，除去重力，另外两个力的方向都发生变化的情况下，判断力的大小变化情况.对于此类问题无法通过“旋转法”解答，可以通过“相似法”判断另外两个力的大小变化.由于在得到力的三角形的过程中大都是通过平移的方式，因此便较容易找到与“力的三角形”相似的“几何三角形”.

2 案例分析

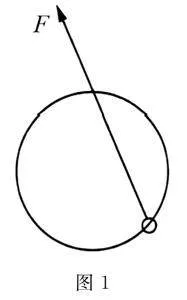
例1 如图1所示，在竖直平面的固定光滑圆轨道的最高点有一个光滑的小孔，质量为m的小环套在圆轨道上，用细线通过小孔系在环上，缓慢拉动细线，使环沿轨道上移，在移动过程中拉力F和轨道对小环的作用力N的大小变化情况是（ ）

（A）F不变，N增大. （B）F不变，N不变.

（C）F减小，N不变. （D）F增大，N减小.

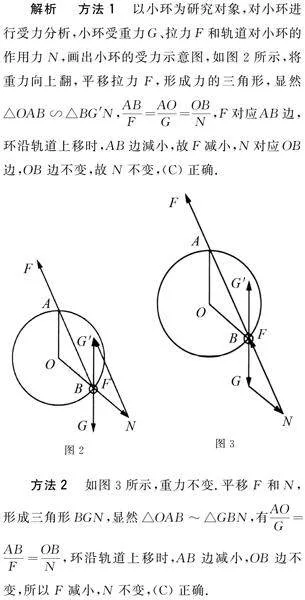
解析 方法1 以小环为研究对象，对小环进行受力分析，小环受重力G、拉力F和轨道对小环的作用力N，画出小环的受力示意图，如图2所示，将重力向上翻，平移拉力F，形成力的三角形，显然△OAB∽△BG′N，ABF=AOG=OBN，F对应AB边，环沿轨道上移时，AB边減小，故F减小，N对应OB边，OB边不变，故N不变，（C）正确.

方法2 如图3所示，重力不变.平移F和N，形成三角形BGN，显然△OAB～△GBN，有AOG=ABF=OBN，环沿轨道上移时，AB边减小，OB边不变，所以F减小，N不变，（C）正确.

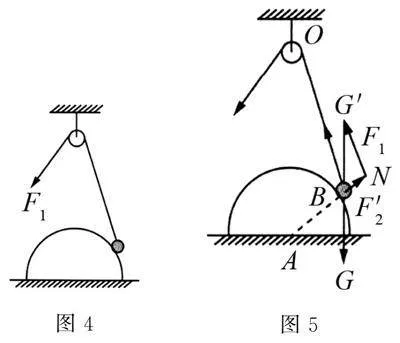
例2 如图4所示，光滑半球的半径为R，有一质量为m的小球用一细线挂靠在半球上，细线上端通过一个定滑轮，在用力将小球缓慢往上拉的过程中，细线对小球的拉力大小F1和小球紧压球面的力F2的变化情况是（ ）

（A）两者都变小.

（B）两者都变大.

（C）F1变小，F2不变.

（D）F1不变，F2变小.

解析 对小球进行受力分析，如图5所示，小球受重力G，细线对小球的拉力F1，球面对小球的支持力F2′，将重力向上翻折，构建力的三角形△G′BF2′，显然△OAB～△G′BN，F′2对应AB边，AB边等于半径，所以F2′大小不变，由于F2′与F2大小相等，可知F2不变.F1对应OB边，当小球沿着球面上移时，OB边减小，故F1减小，（C）正确.

点评 结合例1和例2来看，题目均为平衡问题中的动态变化分析问题，在小球移动过程中F与N不垂直，可运用相似三角形法进行分析，相似三角形法是解决此类问题的一种典型方法，学生要学会应用.在解决问题的关键在于需要学生判断出轨道对于受力对象施加力的方向，从而构建正确的相似三角形.

3 解题步骤总结

在力学问题中，特别是在解决静力学平衡问题时，经常需要通过图形化的方法分析和计算多个力的合成.解题过程可分为五个步骤：（1）将重力向量垂直向上翻转，以符合物理图形表示的常规方向；（2）选择剩余的两个力中的任意一个力进行平移，以便与另外两个力的作用点对齐，从而形成一个力的三角形构图；（3）通过几何学中的平移变换，寻找与力的三角形相似的几何三角形，这通常是在同一平面内的一个简单三角形；（4）利用几何学原理，力的三角形与几何三角形之间的对应边成比例，这为力的计算提供了数学基础；（5）通过对几何图形的观察和分析，可以推断出力的合成情况，以及各力之间的关系，从而揭示整个系统的力学状态.

4 结语

相似三角形解题方法为高中物理动态平衡问题提供了一种直观有效的解决途径.通过对具体试题的分析，展示了该方法在实际问题中的应用效果.该方法不仅有助于学生理解力的合成原理，提高解题能力，也为高中物理教师的教学提供了新的视角.

参考文献：

[1]李伟锋.高中物理动态平衡问题的解法研究[J].中学生数理化（自主招生），2019（12）：29.

[2]侯志敏.巧用数学方法求解物理问题[J].数理化解题研究，2019（31）：72-73.

[3]黄祖德.高中物理题的“难题易解”思维[J].中学生理科应试，2019（03）：27-30.