分类破解热力学第一定律与气体图象的综合问题

【摘要】高中物理热学知识体系较为复杂，抽象程度高，不利于学生的直观理解，尤其是热力学第一定律与气体图象的综合题更是让不少学生无从下手.本文结合实例分类研究四类经典综合题型，以求在解题过程中让学生理解解题思路，归纳解题策略，从而提高物理学科核心素养.

【关键词】热力学第一定律；气体图象；高中物理

1 典例分析

类型1 热力学第一定律与气体p－V图象的综合

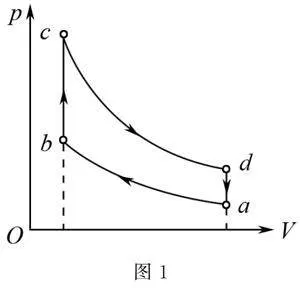
例1 奥托循环是汽车四冲程内燃机常用的工作方式，它包含了两个绝热过程和两个等容过程.图1所示为一定质量的理想气体在奥托循环中的状态变化，关于该气体下列说法中正确的是（ ）

（A）在状态a和c时的内能可能相等.

（B）在a→b过程中，外界对气体做的功等于内能的增量.

（C）在b→c过程中内能的增量小于d→a过程中内能的减少量.

（D）在循环过程中Q吸<Q放.

解 由图象得c→d过程为绝热膨胀过程，则Q=0，W<0.由热力学第一定律ΔU=W+Q得ΔU<0，理想气体的内能只与温度有关，故T减小.d→a的过程为等容过程，p减小，则T减小，故TC>TA，选项（A）错误.

a→b过程为绝热压缩过程，W>0，Q=0，则ΔU=W，即外界对气体做的功等于内能的增量，选项（B）正确.

p－V图象与横坐标轴所围面积即为做功的多少，图象中b→c→d→a围成的图形的面积为气体对外做的功，整个过程中ΔU=0，则ΔW+ΔQ=0，ΔW<0，ΔQ>0，即循环过程中Q吸>Q放，则b→c过程中内能的增量大于d→a过程中内能的减少量，选项（C）（D）错误.

类型2 热力学第一定律与气体T－V图象的综合

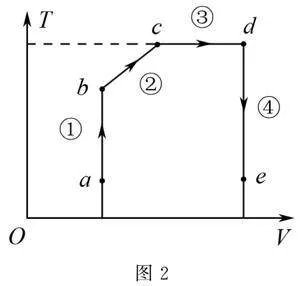
例2 如图2，一定质量的理想气体从状态a开始，经历过程①，②，③，④到达末态e.关于该气体下列说法中正确的是（ ）

（A）过程①中气体压强pa>pb.

（B）过程②中气体对外界做负功.

（C）过程④中气体从外界吸收热量.

（D）气体压强pd<pb.

解 过程①中，V不变、T增大，则p增大，选项（A）错误；

过程②中，V变大，气体对外界做正功，选项（B）错误；

过程④中，T减小，U减小，V不变，W=0，由ΔU=W+Q得Q<0，即气体放出热量，选项（C）错误；

分别作出状态b，c，d的等压线，分析得pb>pc>pd，故选项（D）正确.

类型3 热力学第一定律与气体p－T图象的综合

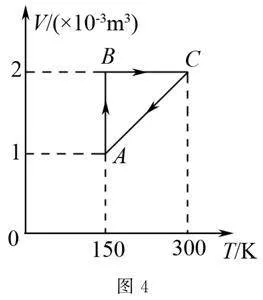
例3 如图3所示是一定质量的理想气体由状态a经历等温或等压过程ab，bc，cd，da再回到原状态的p－T图象.对角线ac的延长线过原点O，下列说法中正确的是（ ）

（A）气体在c点的体积小于a点.

（B）气体在c点的内能小于a点.

（C）cd过程中放热量大于外界对气体所做的功.

（D）da过程中吸收的热量小于外界对气体所做的功.

解 因为ac的延长线过原点O，所以Oca为一条等容线，Va=Vc，选项（A）错误；

理想气体的内能只与温度有关，故在Ua>Uc，选项（B）正确；

cd是等温过程，ΔU=0，由ΔU=W+Q得气体对外放出的热量等于外界对气体做的功，选项（C）错误；

da过程ΔU>0，从外界吸收的热量大于气体对外界做的功，选项（D）错误.

类型4 热力学第一定律与气体V－T图象的综合

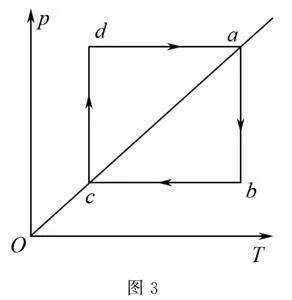
例4 如图4所示，一定质量的理想气体经历A→B→C→A的过程，已知PA=2.0×105Pa，过程中气体对外界放出61.4J的热量.试求该气体在A→B过程中对外界做的功.

解 整个过程中，外界对气体做功W=WAB+WCA，且WCA=pA（VC－VA）.

由热力学第一定律ΔU=W+Q得WAB=－（Q+WCA）=－138.6J，即气体对外界做的功为138.6J.

2 解题要点

要点1 理解热力学第一定律

热力学第一定律，其表述为：系统从外界吸收的热量，一部分使系统内能增加，另一部分对外做功.数学表达式为Q=ΔU+W，其中Q是系统吸收的热量，ΔU是系统内能的增量，W是系统对外做的功.解题时首先要明确系统是否与外界有热量交换以及系统是否对外做功或外界对系统做功.然后就能够依据热力学第一定律的表达式，计算出系统内能的变化量.

要点2 掌握气体图象问题的分析方法

气体图象问题通常涉及到气体的压强、体积、温度等状态参量的变化关系.例如在p－V图上，如果图象是一条双曲线，则说明气体的温度保持不变.

要点3 注意单位换算和正负号的处理

单位换算和正负号的处理是非常重要的.例如温度的单位可能是摄氏度或开尔文，需要依据题目条件进行转换.在热力学第一定律的表达式中热量Q和做功W的正负号表示了能量是增加还是减少.

3 结语

综合上述解题过程和要点分析可知，处理此类问题首先要深入理解热力学第一定律中物理量的含义，以及如何将其变化量的大小在气体图象中体现出来.通过不断地练习和总结，学生会在过程中提高解决问题的能力和物理学科核心素养.

参考文献：

[1]刘跃.例析热力学第一定律的理解与应用[J].数理天地（高中版），2024（08）：20-21.

[2]张志娟.用微专题突破气体实验定律和热力学第一定律的有关问题[J].高中数理化，2020（24）：48-49.

[3]赵九华.理想气体计算问题的基本题型及解法探析[J].高中数理化，2017（07）：29-31.