受力分析的两种方法及其应用探索

【摘要】受力分析是高中物理教学中的重要内容，对于培养学生的物理思维和解题能力具有重要意义.本文对受力分析中的两种方法——隔离法和整体法，进行深入探讨，并通过实例展示它们在高中物理解题中的应用，旨在为物理教学和学习提供有益的参考，引导学生掌握这两种方法，并培养他们灵活运用这些方法解决实际问题的能力.

【关键词】高中物理；受力分析；解题方法

1 引言

受力分析是高中物理教学中的重要内容，隔离法和整体法是两种常用的方法.隔离法通过对物体进行单独分析，可以清晰地了解每个物体所受的力，适用于解决简单问题；整体法是将多个物体视为一个整体，通过分析整体受力情况，可以解决更为复杂的问题.本文将对这两种方法进行深入探讨，并通过实例展示它们在高中物理解题中的应用，以期为物理教学和学习提供有益的参考.

2 隔离法和整体法的概述

隔离法是将研究对象从周围物体中分离出来，单独进行分析的方法.这种方法通常用于分析单个物体或系统中的某个部分的受力情况.通过隔离，可以清晰地识别出作用在研究对象上的所有力，包括已知力和未知力，从而为求解力或运动方程提供基础.整体法是将多个物体或系统的多个部分视为一个整体进行分析的方法.这种方法通常用于分析多个物体组成的系统的受力情况，特别是当系统内部的相互作用力可以忽略不计时.两种方法的选择取决于问题的具体需求和简化问题的可能性.在实际问题中，隔离法和整体法可以结合使用，以简化问题的复杂性，使得问题更易于解决.

3 案例分析

例1 质量为m1和m70BjajCQi2wAD4SgWJZBZg==2的两木块分别被两轻质弹簧连接（不拴接），弹簧劲度系数分别为k1和k2，如图1所示顺序放置，此时整个系统处于平衡状态.某时刻缓缓向上提质量为m1的木块，直至其离开上面的弹簧.则m2移动的距离为（ ）

（A）m1gk1. （B）m2gk1.

（C）m1gk2. （D）m2gk2.

解析 本题主要考查胡克定律的应用，考查合理选择研究对象，并能进行正确的受力分析.求下面弹簧原来的压缩量时，应把m1，m2看作一个整体，下面弹簧的压缩量x1=m1+m2gk2.m1脱离弹簧后，把m2作为对象，则下面弹簧的压缩量x2=m2gk2.下面木块移动的距离d=x1－x2=m1gk2，（C）选项正确.

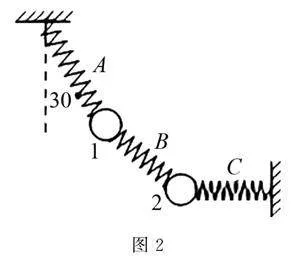
例2 如图2所示，用完全相同的轻弹簧A、B、C将两个小球1，2连接并悬挂，小球均处于静止状态，小球1，2的质量分别为2m和m.弹簧A与竖直方向的夹角为30°，弹簧C水平，则弹簧A，B，C的伸长量之比为（ ）

（A）3∶4∶2. （B）4∶3∶2.

（C）23∶2∶3. （D）23∶1∶3.

解析 把小球1和小球2隔离，对它们分别受力分析，设弹簧A，B，C的拉力分别为FA，FB，FC，弹簧B的拉力与竖直方向的夹角为α，如图3所示.

由平衡条件，对小球1：FAsin30°=FBsinα，FAcos30°=2mg+FBcosα.对小球2：FBsinα=Fc，FBcosα=mg.联立解得：FA=23mg，FB=2mg，FC=3mg.根据胡克定律F=kx，k相同，则弹簧A，B，C的伸长量之比等于三个弹簧的拉力之比，即有xA∶xB∶xC=FA∶FB∶FC=23∶2∶3.故选（C）.

例3 如图4所示，设A重10N，B重20N，A，B间的动摩擦因数为0.1，B与地面的摩擦因数为0.2.问：至少对A向左施多大的力，才能使A，B发生相对滑动？

解析 当A，B发生相对滑动时，它们之间的摩擦力达到最大静摩擦力.

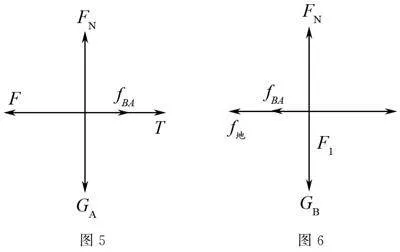
图5是A的受力分析图，图6是B的受力分析图.对B受力分析，水平方向受A对B的摩擦力和地面对B的摩擦力和绳子拉力，则有：T=fAB+f地.因为fAB=μ1GA=1N，f地=μ2GA+GB=6N，则T=7N.对A进行受力分析，水平方向受向左施加的拉力、B对A向右的摩擦力和绳子对A向右的拉力，F=T+fBA=8N.因此至少对A向左施加8N的力，才能使A，B发生相对滑动.

4 结语

通过本文的探讨，学生可以看到隔离法和整体法在受力分析中的重要性和实用性.隔离法能够清晰地展示每个物体所受的力，帮助学生建立对物体受力的直观理解；整体法则能够简化复杂问题，提高解题效率.在实际应用中，需要根据问题的具体情况选择合适的方法，并灵活运用.此外，对于一些复杂问题，结合使用隔离法和整体法能够达到更好的解题效果.在高中物理教学中，教师应注重引导学生掌握这两种方法，并培养他们灵活运用这些方法解决实际问题的能力.

参考文献：

[1]吕高美.借助整体法高效解答高中物理力学试题[J].高中数理化，2023（S1）：113-114.

[2]刘文煜.妙用整体法与隔离法解决夹砖问题[J].初中生辅导，2023（08）：63-65.

[3]杨攀，刘松.例谈“受力分析”在初中力学解题中的有效应用[J].数理化学习（初中版），2023（03）：43-46.