非质点类机械能守恒问题的解题策略

【摘要】本文深入探讨非质点类机械能守恒问题，详细阐述“液柱”类模型、“软绳”类模型和“链条”类模型的机械能守恒问题及相应的解题策略．通过对各种典型实例的分析，强调正确选择系统、细致分析能量转化、准确判断守恒条件以及合理运用相关物理量的重要性．旨在为解决非质点类机械能守恒问题提供有效的方法和思路，以提升对该类问题的理解和处理能力．

【关键词】机械能守恒；高中物理；解题策略

机械能守恒定律是物理学中的重要定律之一，在解决众多物理问题中具有关键作用．然而，当涉及到非质点类物体时，问题的复杂性增加，需要特定的策略和方法来准确求解．对非质点类机械能守恒问题的深入研究具有重要的理论和实践意义．

1 “液柱”类模型中的机械能守恒问题

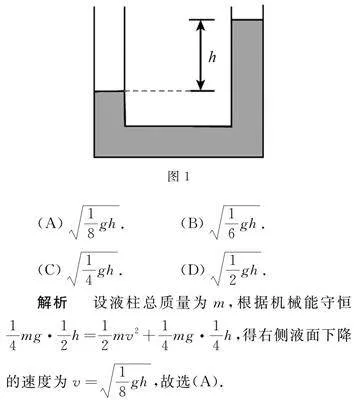
例1 如图1所示，粗细均匀、两端开口的U形管内装有同种液体，管中液柱总长度为4h，开始时使两边液面高度差为h，后来让液体自由流动，当两液面高度相等时，右侧液面下降的速度为（ ）

（A）18gh. （B）16gh.

（C）14gh.（D）12gh.

解析 设液柱总质量为m，根据机械能守恒14mg·12h=12mv2+14mg·14h，得右侧液面下降的速度为v=18gh，故选（A）．

解题策略 运用机械能守恒定律解决“液柱”类模型问题时，确定重力势能是关键，需要分段确定其重心和质量，进而确定重力势能．

2 “软绳”类模型中的机械能守恒问题

例2 如图2所示，总长为l、质量为m的均匀软绳对称地挂在轻小滑轮上，用细线将质量也为m的物块与软绳一端连接．现将物块由静止释放，直到软绳刚好全部离开滑轮．不计一切摩擦，重力加速度为g，下列说法正确的是（ ）

（A）刚释放物块时，细线的拉力大小等于mg.

（B）在软绳从静止到刚离开滑轮的过程中，软绳的机械能守恒.

（C）在软绳从静止到刚离开滑轮的过程中，物块的机械能减少了18mgl.

（D）在软绳从静止到刚离开滑轮的过程中，软绳的机械能增加了38mgl.

解析 刚释放的时候，物块是有向下的加速度的，根据牛顿第二定律有mg－T=ma，可知拉力小于mg，故（A）错误；在软绳从静止到刚离开滑轮的过程中，拉力对软绳做了功，软绳机械能不守恒，故（B）错误；设软绳刚离开滑轮的时候，物块和软绳的速度为v，根据机械能守恒定律有mg·l2+mg2·l2=12·2m·v2，计算可得v=3gl2，则物块机械能的减少量为E减=mg·l2－12mv2=18mgl，故（C）正确；系统的机械能是守恒的，由于物块的机械能减少了18mgl，所以软绳的机械能增加了18mgl，故（D）错误．

解题策略 高中物理中“绳连接体”模型中，绝大多数情况下绳子为轻绳（不计重力），只需考虑绳连接的物体的重力及其重力势能，但这里给出的“软绳”是质量分布均匀的绳子，确定其重力势能需要找运动过程中的重心，确定了重力势能才能运用机械能守恒定律解题．

3 “链条”类模型中的机械能守恒问题

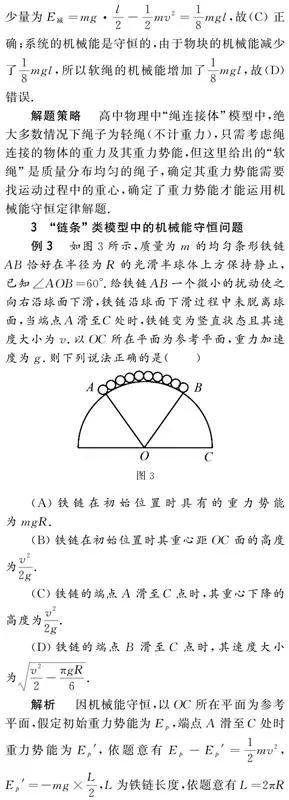
例3 如图3所示，质量为m的均匀条形铁链AB恰好在半径为R的光滑半球体上方保持静止，已知∠AOB=60°．给铁链AB一个微小的扰动使之向右沿球面下滑，铁链沿球面下滑过程中未脱离球面，当端点A滑至C处时，铁链变为竖直状态且其速度大jugTL0i9dcsZPIcjx1seQQ==小为v．以OC所在平面为参考平面，重力加速度为g．则下列说法正确的是（ ）

（A）铁链在初始位置时具有的重力势能为mgR.

（B）铁链在初始位置时其重心距OC面的高度为v22g.

（C）铁链的端点A滑至C点时，其重心下降的高度为v22g.

（D）铁链的端点B滑至C点时，其速度大小为v22－πgR6.

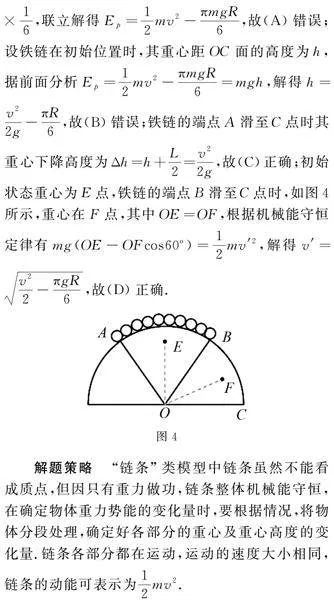
解析 因机械能守恒，以OC所在平面为参考平面，假定初始重力势能为Ep，端点A滑至C处时重力势能为Ep′，依题意有Ep－Ep′=12mv2，Ep′=－mg×L2，L为铁链长度，依题意有L=2πR×16，联立解得Ep=12mv2－πmgR6，故（A）错误；设铁链在初始位置时，其重心距OC面的高度为h，据前面分析Ep=12mv2－πmgR6=mgh，解得h=v22g－πR6，故（B）错误；铁链的端点A滑至C点时其重心下降高度为Δh=h+L2=v22g，故（C）正确；初始状态重心为E点，铁链的端点B滑至C点时，如图4所示，重心在F点，其中OE=OF，根据机械能守恒定律有mg（OE－OFcos60o）=12mv′2，

解得v′=v22－πgR6，故（D）正确．

解题策略 “链条”类模型中链条虽然不能看成质点，但因只有重力做功，链条整体机械能守恒，在确定物体重力势能的变化量时，要根据情况，将物体分段处理，确定好各部分的重心及重心高度的变化量．链条各部分都在运动，运动的速度大小相同，链条的动能可表示为12mv2．

4 结语

非质点类机械能守恒问题虽然具有一定的复杂性，但通过合理的解题策略，可以有效地进行分析和求解．对系统的恰当选择、深入的能量分析、准确的守恒条件判断以及合理的物理量运用是解决此类问题的关键．进一步地研究和实践将有助于更深入地理解和掌握这些策略，从而更好地处理各种复杂的物理问题．

参考文献：

[1]陈卫国.“迁移法”解非质点类机械能守恒问题[J].物理教师，2023，44（06）：96-97.

[2]丁军涛.善用机械能守恒，化繁为简有奇功——例析机械能守恒定律在解题中的应用[J].数理天地（高中版），2022（22）：44-46.

[3]郑周博，劳荆华.回视典例 迁移模型——谈一道绳索问题的另解[J].湖南中学物理，2024，39（03）：75-77.