物体与弹簧的“别离之舞”：动态分离问题研究

【摘要】两体弹簧系统问题是高中物理力学系统中的重要内容，这类问题涉及整体法、隔离法以及牛顿第二定律的应用，分析这类问题需要把握分离的关键条件以及分离时两物体速度、加速度特点，在教学中需要加强这方面的专题训练.本文从模型到方法以及典型例题深入分析，以突破这类问题的难点.

【关键词】弹簧；临界分离；高中物理

1 认清弹簧端的叠加体的动态分离的本质

弹簧端的叠加体的动态分离问题的本质是：

（1）从力的角度来看是支持力和压力的临界，即在两物体分离的瞬间两者之间的相互作用的支持力和压力为零；

（2）从加度速的角度来看是加速度的临界，即两物体在分离的瞬间的加速度是相同的；

（3）从速度的角度来看是速度的临界，即两物体在分离的瞬间的速度是相同的；

（4）从处理方法的角度来看，处理弹簧端的叠加体的动态分离用到的方法是整体法和隔离法.

2 弹簧端的叠加体的动态分离问题的分类处理

2.1 自然状态下的动态分离问题

例1 如图1所示，A，B两物体叠放在弹簧上，现用力向下压B到某位置后释放，试分析判断A，B两物体分离瞬间所在位置？

解析 抓住临界问题的本质：在A，B分离的瞬间，二者的加速度相同，A，B间没有相互作用的支持力和压力.设分离的瞬间弹簧对整体的弹力为F，A的质量为M，B的质量为m.

对A，B整体据牛顿第二定律有：（M+m）g+F=（M+m）a.

对B据牛顿第二定律有：mg=ma由以上两式解得：F=0，即两者在弹簧恢复原长时分离.

2.2 恒力作用下的动态分离问题

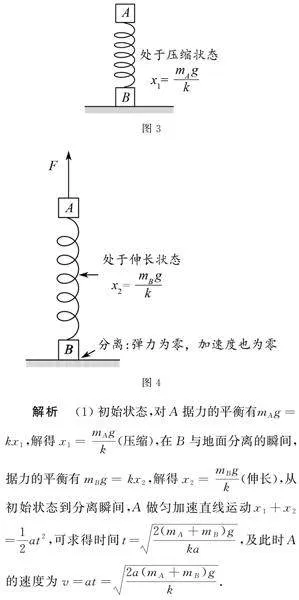
例2 如图2所示，在物体B上施加一恒力F，二者向上运动，试分析判断A，B分离瞬间所在位置？

解析 抓住临界问题的本质：在A，B分离的瞬间，二者的加速度相同，A，B间没有相互作用的支持力和压力.

设分离瞬间弹簧对整体的弹力为F，A的质量为M，B的质量为m.

对A，B整体进行分析，根据牛顿第二定律有：F+kx－（M+m）g=（M+m）a（x为弹簧的形变量）.

对A进行分析，根据牛顿第二定律有：kx－Mg=Ma.

由以上两式解得：kx=MmF，所以A，B分离时弹簧处于压缩状态，弹簧的压缩量x=MFmk.

3 弹簧两端的连接体的动态分离问题

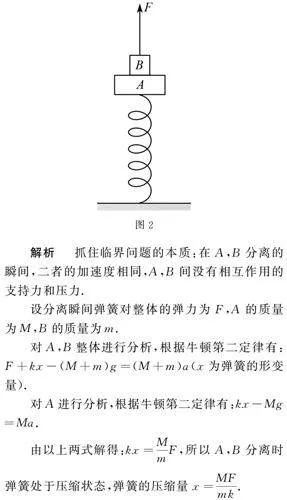
例3 在变力F的作用下物体A以加速度a做匀加速直线运动的情况来研究：

（1）物体A做匀加速直线运动的时间？

（2）分析拉力F和物体A的位移大小间的定量关系？

解析 （1）初始状态，对A据力的平衡有mAg=kx1，解得x1=mAgk（压缩），在B与地面分离的瞬间，据力的平衡有mBg=kx2，解得x2=mBgk（伸长），

从初始状态到分离瞬间，A做匀加速直线运动x1+x2=12at2，可求得时间t=2（mA+mB）gka，及此时A的速度为v=at=2a（mA+mB）gk.

（2）当力F刚作用在物块A上的瞬间，对A由牛顿第二定律有F－mAg+kx1=mAa，解得F=mAa，当弹簧在压缩阶段据牛顿第二定律有F－mAg+k（x1－x）=mAa（x为A的位移），得F=kx+mAa.当弹簧在伸长阶段据牛顿第二定律有F－mAg－k（x－x1）=mAa（x为A的位移），得F=kx+mAa，由此可见F随物体A的位移均匀增加.

例4 如图5所示，A，B两小球在竖直方向上通过劲度系数为k的轻质弹簧相连，B球放在水平地面上，整个系统处于竖直静止状态.现用竖直向上的拉力F缓慢将A上提，直至B恰好离开地面.已知A，B的质量均为m，重力加速度为g.在此过程中拉力做的功（ ）

（A）2mg2k. （B）2mg23k.

（C）3mg22k. （D）mg2k.

解析 原来系统静止时弹簧处于压缩状态，B恰好离开地面时弹簧处于伸长状态，由于A，B的质量均为m，设弹簧的压缩量和伸长量均为x，由胡克定律F=kx，可得x=mgk.

弹簧压缩时的弹性势能与伸长时的弹性势能相等，在此过程中拉力做的功等于系统机械能的增量W=ΔE=mgh=mg×2×mgk=2mg2k，故选（A）.

点评 对小球A初位置分析可以求出弹簧压缩量，小球B将要离开地面瞬间，合外力为零，可以求出弹簧伸长量，由于初末位置弹簧形变量相等，弹簧弹性势能相等，然后结合小球A上升的高度即可求出系统机械能增量.

4 结语

弹簧端物体分离的关键是分离瞬间之间的弹力为零，加速度相等.如果是两物体的分离，则两物体的速度、加速度均相等；如果是物体与某一接触面分离，此时他们之间弹力为零，加速度相等；如果接触面是静止不动的，则与之分离的物体加速度和速度均为零.处理这类问题需要把握分离关键条件，结合牛顿第二定律、整体法、隔离法进行列式求解.