带电粒子在叠加场中的运动问题分类突破

【摘要】带电粒子在叠加场中的运动问题是高中物理的难点之一.本文对带电粒子在叠加场中的运动问题进行分类突破，以期为学生提供有益的参考.

【关键词】高中物理；带电粒子；叠加场

在物理学习中，带电粒子在叠加场中的运动问题是一个重要的知识点，它涉及磁场、电场、重力场等多个场的叠加，综合性强，难度较大，只有掌握了准确的处理方法才不容易出错.

1 带电粒子在叠加场中的直线运动

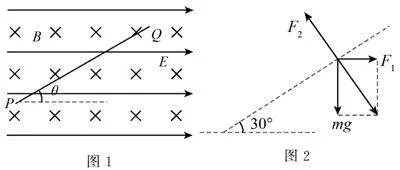
例1 在地面上方存在相互正交的匀强磁场和匀强电场，其中磁感应强度B=1T，电场强度E=5N/C，方向如图1所示.一质量为m=0.5g、电荷量未知的带正电小球恰好沿与水平方向成θ=30°的PQ方向由P向Q做直线运动，重力加速度g=10m/s2.求：

（1）带电小球的电荷量和速率；

（2）当小球运动到Q点时撤去匀强磁场，此时Q距地面的高度为h=10m，求小球落地点距Q点的水平距离.（不考虑撤去磁场时对电场的影响）

解析 （1）由题意可知，带电小球受力平衡，如图2所示.

F1为小球受电场力，F2为小球受洛伦兹力，因此可知小球带正电，

由图可得F1=qE=mgtan30°，

F2=qvB=mgcos30°=0.5×10－3×1032N

=3×10－23N，

解得q=mgtan30°E=33×10－3C，

v=F2qB=3×10－233×10－33×1m/s=10m/s.

（2）当小球运动到Q点撤去匀强磁场，则有小球在水平方向做匀加速直线运动，在竖直方向小球做竖直上抛运动，

则有x=vcos30°t+12at2，

y=vsin30°t－12gt2，

又有a=qEm=33×10－3×50.5×10－3m/s2=1033m/s2，

代入数据解得t=2s，t=－1s（舍去），

则有x=5033m.

评析 因洛伦兹力与速度有关，所以，有洛伦兹力参与的直线运动一定为匀速直线运动，可见，粒子由P向Q的运动过程中受力平衡.

2 带电粒子在叠加场中的圆周运动

例2 图3和图4是两个完全相同的竖直半圆形光滑绝缘轨道，其中M点和N点为两轨道的最低点，在图3轨道所在的平面内有垂直于平面的匀强磁场，在图4轨道所在的平面内有平行于平面向右的匀强电场，现将两个可视为质点的相同带正电小球a、b分别从各自轨道的右侧最高点处由静止释放，在它们从释放到首次到达各自的最低点的过程中，下列选项正确的是（ ）

（A）b球下滑的时间比a球长．

（B）下滑过程中两球机械能均守恒．

（C）b球在N点的速度大于a球在M点的速度．

（D）b球对N点的压力大于a球对M点的压力．

解析 因洛伦兹力不做功，小球在磁场中仅有重力做功，所以a球的机械能守恒；小球在电场中从最高点运动到最低点的运动过程中，电场力做负功，机械能减小，到最低点时的速度相对较小，b球在N点的速度小于a球在M点的速度，在电场中运动的时间也相对较长，（A）选项正确，（B）（C）选项错误；小球a在磁场中的最低点：FM－mg－BqvM=mv2Mr，解得FM=mv2Mr+mg+BqvM，小球b在电场中的最低点：FN－mg=mv2Nr，解得FN=mv2Nr+mg，因为vM>vN，可得FM>FN，（D）选项错误.

评析 粒子在图3和图4的两个竖直面内都做圆周运动，但是运动规律不同，图3中的小球受到重力和指向圆心的洛伦兹力，其中洛伦兹力始终不做功，对粒子的速度大小无影响，机械能守恒，而处在图4环境中的粒子相当于在“等效重力场”中运动，其速度会受到电场的影响.

3 突破带电粒子在叠加场中的运动问题的基本思路

首先，明确叠加场的性质.叠加场通常是由电场、磁场以及重力场中的两个或三个场叠加而成.仔细分析每个场的特点，如电场力的方向与大小取决于电场强度和粒子的电荷量；洛伦兹力的大小为qvB，方向始终与速度方向垂直；重力的大小和方向则较为固定.

其次，进行受力分析.这是解决问题的关键步骤.根据带电粒子的电性、速度方向以及各个场的方向，确定粒子所受的电场力、洛伦兹力和重力.如果粒子的速度大小或方向发生变化，洛伦兹力也会随之改变，所以要动态地进行受力分析.

接着，判断粒子的运动状态.根据牛顿第二定律，合力决定了粒子的加速度.若合力为零，粒子将做匀速直线运动；若合力大小不变，方向始终与速度方向垂直，粒子将做匀速圆周运动.

然后，选择合适的解题方法.对于直线运动，可以利用牛顿运动定律结合运动学公式求解；对于圆周运动，要确定圆心、半径和周期，通常利用洛伦兹力提供向心力的公式来求解；对于复杂的曲线运动，可以考虑能量守恒定律或动能定理.

最后，进行结果的分析与讨论.检查所得结果是否符合实际情况，同时，可以对不同的参数进行讨论，分析其对粒子运动的影响.

4 结语

带电粒子在叠加场中的运动问题综合性强，难度较大.在解题过程中，需要注意粒子在各个场中的受力情况，以及粒子的初始条件和边界条件等因素的影响.对这类问题要归类后各个击破，逐步掌握解题技巧，提高解题能力.同时，建议学生多做相关练习，积累解题经验，加深对知识点的理解和掌握.

参考文献：

[1]惠梦苏，刘新选.带电体在组合场和叠加场中运动问题归类分析[J].中学物理教学参考，2021，50（01）：67-70.

[2]胡连冬.带电粒子在正交叠加场中运动问题的研究[J].数理化解题研究，2020（04）：57-59.

[3]单鹏杰.浅析带电粒子在叠加场中运动问题的求解策略[J].中学生数理化（学习研究），2019（01）：75.

[4]韩兴乾，喻梅琴.例析带电体在组合场和叠加场中的运动[J].试题与研究，2017（31）：15-18.