含弹簧连接体的动力学问题探讨

【摘要】本文深入研究含弹簧连接体的动力学问题，通过对竖直面内和斜面上的弹簧连接体问题的详细分析，探讨弹簧的弹力对系统内物体运动的影响，并结合具体实例进行深入剖析，以展现该类问题在物理学中的重要性和复杂性.

【关键词】弹簧连接体；初中物理；解题技巧

在物理学中，连接体问题一直是一个重要的研究领域，而含弹簧连接体的动力学问题因其独特的特点和广泛的应用而备受关注.对这类问题的研究不仅有助于深入理解力学的基本原理，也在众多实际应用中具有关键意义.

1 竖直面内恒力作用下物体的非匀变速直线运动

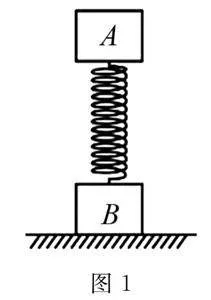
例1 如图1所示，小物块A和B通过轻质弹簧相连接，竖直静置于水平地面上.若给小物块A一竖直方向的瞬时冲量，其大小为3N·s，随后B恰好不能离开地面.已知A，B质量分别为1kg、2kg，弹簧的劲度系数k=100N/m，弹簧始终处于弹性限度内，重力加速度g取10m/s2.

（1）从开始至B恰好不离开地面的过程，求弹簧弹性势能的变化量；

（2）若用大小为17.4N的竖直向上恒力作用于A，使之由静止开始运动，直至B刚离开地面时，求A的速度大小.

解析 （1）初始小物块A静止时，弹簧压缩x1，

则mAg=kx1，代入得x1=0.1m.

小物块B恰好不能离开地面，弹簧伸长x2，

则mBg=kx2，代入得x2=0.2m.

对小物块A提供竖直向下的瞬时冲量I，

则I=mAv，代入得v=3m/s.

小物块B恰好不离开地面的过程中，小物块A、小物块B、轻弹簧和地球系统机械能守恒，

则12mAv2=mAgx1+x2+E弹，

代入得E弹=1.5J.

（2）由题知，未用力F拉动时，A，B静止，小物块A静止时，弹簧压缩x1，小物块B恰好不能离开地面，弹簧伸长x2，由动能定理知Fx1+x2－E弹－mAgx1+x2=12mAv2A，代入得vA=1.2m/s.

点评 竖直面内弹簧连接体在恒力作用下，因弹簧的弹力是变力，对系统内每个物体而言，加速度大小是变化的，需要运用能量观点来解决问题.

2 竖直面内恒力作用下的临界问题

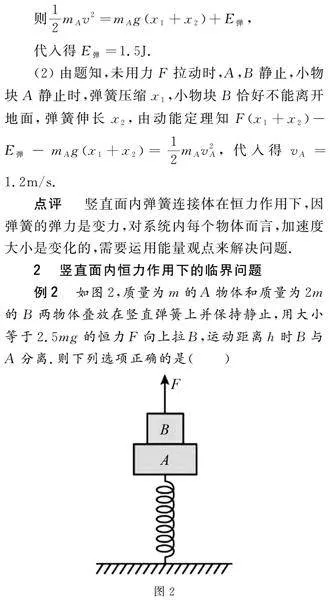
例2 如图2，质量为m的A物体和质量为2m的B两物体叠放在竖直弹簧上并保持静止，用大小等于2.5mg的恒力F向上拉B，运动距离h时B与A分离．则下列选项正确的是（ ）

（A）B和A刚分离时，弹簧弹力为1.25mg．

（B）B和A刚分离时，A、B间弹力为mg．

（C）B和A刚分离时，A的加速度为0.25g．

（D）弹簧的劲度系数等于7mg2h．

解析 B与A刚分离的瞬间，A、B仍具有相同的速度和加速度，且A、B间无相互作用力.对B分析知，B具有向上的加速度F－2mg=2ma，解得a=0.25g，此时对A分析有F弹－mg=ma，解得F弹=1.25mg，且处于压缩状态，（A）（C）正确，（B）错误；B和A刚分离时，弹簧处于压缩状态，F弹=1.25mg，原来静止时弹力大小为3mg，则弹力减小量ΔF=3mg－1.25mg=1.75mg，两物体向上运动的距离为h，则弹簧压缩量减小Δx=h，得k=ΔFΔx=7mg4h，（D）错误.

点评 弹簧连接体中叠加物体的分离问题，需要先分析物体在运动过程中的受力情况，再进行运动分析，分析运动过程中体恰好分离的临界条件（叠加体之间的弹力为0），进而运用牛顿运动定律求解.

3 斜面上恒力作用下的临界问题

例3 如图3所示，轻质弹簧一端固定在光滑斜面底端，另一端与物块A拴接，物块B、C用跨过光滑定滑轮的轻绳相连，与B相连的轻绳与斜面平行，开始时用手托住物块C，三个物块均保持静止，绳刚好伸直且无拉力，C距地面足够高.三个物块均可视为质点.已知斜面倾角为θ=37°.物块A、B、C的质量分别为mA=1kg、mB=3kg、mC=2kg.弹簧的劲度系数k=100N/m，g取10m/s2.从释放C的瞬间开始计时，则（ ）

（A）释放物块C的瞬间，物块C的加速度为0.4m/s2．

（B）释放物块C的瞬间，物块C的加速度为103m/s2．

（C）当物块C下落的高度为0.24m时，物块A、B恰好分离．

（D）物块A、B分离时，物块C的速度约为0.81m/s．

解析 根据牛顿第二定律mCg=（mA+mB+mC）a，解得释放物块C的瞬间，物块C的加速度a=103m/s2，故（B）正确，（A）错误；释放C时，根据平衡条件可得kx1=（mA+mB）gsinθ，解得x1=625m，物块A，B恰好分离时，A，B之间的弹力为零，对A根据牛顿第二定律kx2－mAgsinθ=mAa′，对B，C整体根据牛顿第二定律mCg－mBgsinθ=（mC+mB）a′，联立解得x2=0.064m，物块A，B恰好分离时物块C下落的高度h=x1－x2=0.176m，对从释放C到A，B恰好分离的过程，根据动能定理12kx21－12kx22+mCg（x1－x2）－（mA+mB）gsinθ·（x1－x2）=12（mA+mB+mC）v2，解得v=0.81m/s，故（D）正确，（C）错误.

点评 本题中，因物块C的质量恒定，因此物块B受到绳子的拉力恒定，释放物块C的瞬间，运用牛顿第二定律求解其加速度，物块A，B分离的瞬间，他们之间的弹力为0，运用能量观点求解其速度的大小.

4 结语

含弹簧连接体的动力学问题是物理学中一个具有挑战性的问题.通过对其动力学原理和求解方法的探讨，以及结合具体实例的分析，深入理解了这类问题的复杂性和多样性.在实际应用中，含弹簧连接体的动力学特性具有广泛的用途，对于工程技术和科学研究都具有重要的价值.未来，随着科学技术的不断发展，对含弹簧连接体问题的研究将继续深入，为解决更多实际问题提供理论支持和技术保障.

参考文献：

[1]黄尚鹏.弹簧连接体问题的分析及拓展[J].中学物理教学参考，2023，52（01）：29-34.

[2]吕迎春.刍议连接体模型求解策略[J].中学生数理化（学习研究），2018（09）：51.

[3]刘大明，江秀梅.连接弹簧的连接体分离问题的再剖析[J].理科考试研究，2020，27（07）：37-38.