温度边界条件对平面壁板热屈曲行为的影响研究
摘 要:以高超声速飞行器为代表的高速航空器在飞行过程中其壁板结构易发生屈曲失稳,这种屈曲失稳与热效应紧密相关,因此温度边界条件会对结构的屈曲行为产生影响。本文通过一套自主设计的试验夹具,结合基于热力顺序耦合方式的静力弧长算法,研究了不同温度边界条件对平板屈曲行为的影响。结果表明,边界温度会显著影响极限屈曲载荷,且影响程度与力学边界条件相关;当边界与域内存在负温差(边界温度低于域内温度)时,温度影响的敏感程度更高;相比之下,边界温度影响区的宽度对壁板屈曲行为的影响较小。本文可为复杂壁板结构热屈曲行为的深入研究提供一定的参考依据。
关键词:平板屈曲; 热力耦合边界; 弧长法; 边界温度; 极限屈曲载荷
中图分类号:V214.3 文献标识码:A DOI:10.19452/j.issn1007-5453.2024.08.006
基金项目: 航空科学基金(20200009057004)
高超声速飞行器具有超过Ma 5的超快飞行速度,可以做到很高的突防成功率和侦察效能,但其快速飞行时产生的严酷气动加热环境使得机身和机翼除了要承受复杂的机械载荷,还要承受外表面气动加热引起的热梯度以及受约束的热膨胀的作用,导致其结构容易产生屈曲问题[1],从而对壁板动力学响应产生不可忽略的影响[2-3],因此热效应对壁板屈曲行为的影响值得研究。
针对结构屈曲失稳问题,国内外学者先后发展了圆柱薄壳初始缺陷非线性理论、载荷与挠度的非线性跳跃论、初始后屈曲理论[4]等,且提出了不同的屈曲计算方法。孙家斌[5]基于Donnell壳体理论建立了一种能量守恒的解析算法,用于求解弹性圆柱壳、弹塑性圆柱壳和功能梯度圆柱壳在各类载荷作用下的屈曲问题。侯瑞等[6]基于金属结构的张力场理论提出了一种适用于复合材料翼梁的后屈曲计算方法,此方法也可用于复合材料机身壁板的后屈曲计算。Hutchinson等[7]研究了均匀径向压力引起的周向薄膜应力对轴压圆柱壳临界屈曲载荷折减因子的影响。Virot等[8]研究了凹坑缺陷对于结构屈曲强度的影响,并分析了圆柱壳在不同轴向压力作用下发生屈曲所需要克服的能量壁垒。
中国飞机强度研究所在飞行器关键部件的屈曲研究方面做了大量的工作。针对飞行器加筋壁板在不同载荷工况下的结构稳定性问题,建立了多种加筋壁板有限元数值分析模型并开展稳定性分析[9];采用一体化热防护系统(ITPS)承力结构的方法,开发了参数化建模程序,并研究了镂空腹板对ITPS承载能力及隔热性能的影响[10];开展了平板加热虚拟试验,实现了全参数设计的平板加热试验数值仿真,以此进行结构热强度虚拟试验[11]。
目前,在热效应对壁板结构屈曲行为的影响研究中,通常为简化问题采用的是均匀温度场[1,12-13]。而在实际问题中,壁板的边界受夹持,会导致边界附近的温度与内部存在温差,即壁板的温度场不均匀且受温度边界条件的影响,同时有研究指出夹持端的温度边界条件引起的温度分布不均,会进一步引起局部力学性能差异,导致屈曲模态发生改变[14],在此基础上有必要进一步研究温度边界条件对壁板结构屈曲行为的规律。因此,本文采用有限元数值模拟结合试验的方法分析了典型力学约束条件下,温度边界条件对壁板屈曲问题的影响,相关研究成果可为复杂壁板结构热屈曲行为的深入研究提供一定的参考,用于指导高超声速飞行器结构设计。
1 热屈曲试验研究
1.1 热屈曲试验方案
本文所用试验材料为304不锈钢,化学组成成分见表1。从厚板上切下小圆柱作为测试试样,通过Gleeble-3500试验机进行了不同温度下的热压缩试验,以获得基础力学性能;其他热物性参数见参考文献[15]。材料参数见表2。
为开展热屈曲试验,本文设计并制造了适用于小尺寸平板屈曲试验的夹具(三维模型见图1),可实现双边与四边固支和简支的任意搭配;配合加热装置、万能材料试验机INSTRON 2382以及红外热像仪构成一套完整的热屈曲试验平台。热屈曲试验平台如图2所示,屈曲试验夹具被安装在材料试验机上,并由热像仪记录板面全场温度分布,某典型时刻的温度场如图3所示。基于试验平台,开展小尺寸平板屈曲试验,取尺寸为120mm×120mm×1mm的小平板置于加热炉中进行预加热,随后将平板取出至夹具中进行夹持固定,操作期间平板处于空冷状态,最后对平板中心区域使用喷火枪进行加热。试验全程使用热像仪检测板面的温度场。当平板的中心温度到达600℃时进行下压,获得压缩载荷-位移曲线。
1.2 热屈曲试验结果分析
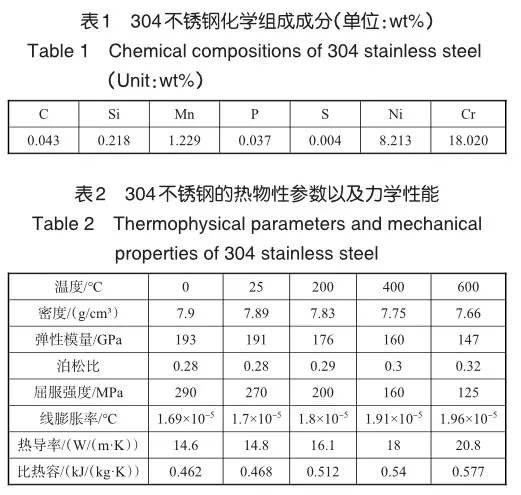
将热像仪记录的温度场数据进一步可视化处理,由于压缩过程时间很短(1s以内),板面温度场变化很小,近似认为压缩过程温度场恒定,取平板开始压缩时刻的温度场作为平板整个压缩过程的近似温度场,如图4所示。平板中心的最高温度区域的平均温度定义为平板的中心温度T1,板面4条边界上温度的平均值定义为边界温度T2。

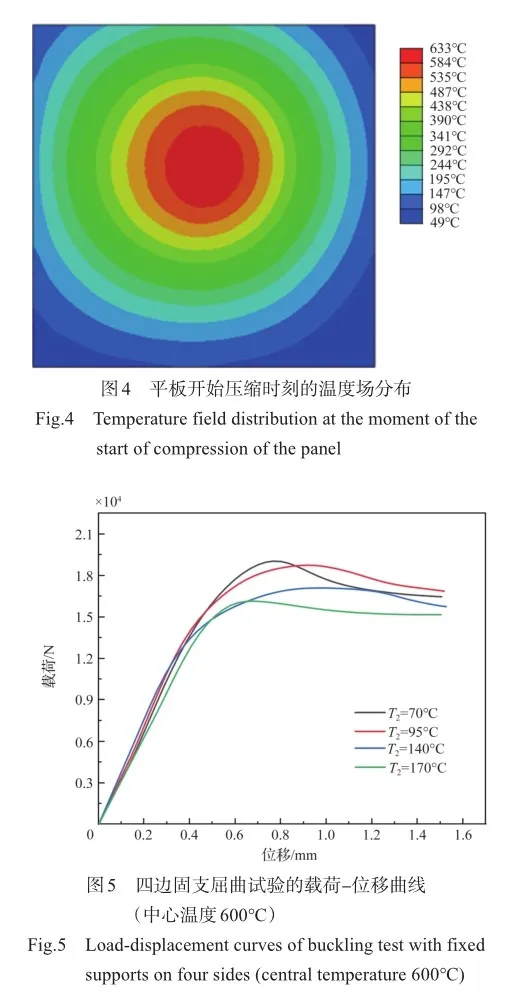
图5给出的是平板中心温度600℃,边界温度分别为70℃、95℃、140℃、170℃时,四边固支情况下的单向压缩屈曲试验的载荷-位移图。对比边界温度为70℃、95℃、140℃、170℃的曲线可以看出,随着边界温度的上升,平板的极限屈曲载荷下降。
2 热屈曲数值模拟
2.1 数值模拟方法
有限元法能够通过将复杂的数学物理问题离散化,通过编程借助计算机来分析复杂的高度非线性问题,因而得到广泛应用[16-18]。本文使用某有限元软件模拟平面壁板的屈曲问题,研究壁板的温度边界条件对屈曲现象的影响。
2.1.1 稳态顺序热力耦合分析理论
屈曲试验压缩前后温度场分布基本不变,表明此壁板对热屈曲问题中由塑性耗散或者相变产生的热量产生的影响较小,且可以视为稳态温度场,应力应变场和温度场更倾向于一种单向耦合的关系,因此可采用稳态温度场问题的顺序热力耦合法[19]。


2.1.3 模拟方法可靠性验证
将顺序热力耦合法和静力弧长法相结合进行求解,并将过程分成线性屈曲分析、稳态传热分析以及非线性屈曲分析三部分。具体求解过程是先通过线性屈曲分析获得壁板模型的一阶屈曲模态并作为初始几何缺陷;再通过稳态传热分析获得模型的稳态温度场结果;最后进行非线性屈曲分析,先使壁板热膨胀,再施加单向压缩直至屈曲,结合初始几何缺陷和稳态温度场,采用静力弧长法对模型的热屈曲行为进行分析。
为验证数值模拟方法的可靠性,依照上述的数值模拟方法建立试验平板的有限元模型(100mm×100mm×1mm的方形平板,材料为304不锈钢),并将屈曲试验中热像仪测定的板面实际温度场直接导入非线性屈曲分析中,替代求解过程中的稳态温度场,完成热屈曲数值模拟分析,得到四边固支情况下屈曲模拟的载荷-位移图(见图6),与屈曲试验的载荷-位移图(见图5)对比可以看出,模拟曲线的变化趋势与试验曲线相近。图6中边界温度为95℃和140℃对应的极限屈曲载荷相近,原因是两种情况下的屈曲模态相近;但边界温度的升高会导致边界软化加剧,需要施加更大的强制位移条件才能达到极限屈曲载荷,故两种温度边界条件下发生屈曲时的位移相差较大。图7给出了不同边界温度下的屈曲试验与模拟的极限屈曲载荷,通过对比可以看出,试验和模拟得到的极限屈曲载荷相近,且随着边界温度的上升,平板的极限屈曲载荷均有所下降。

2.2 模拟研究方案
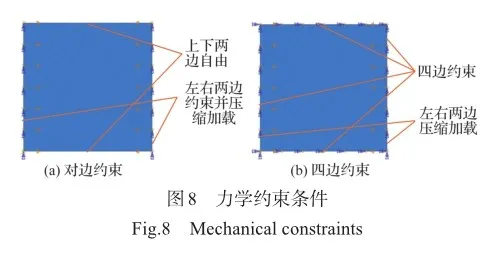
在实际应用中大尺寸平板适用性更广,但对于大尺寸平板屈曲试验,受限于试验平台等因素,试验开展较为困难,故用小平板进行验证数值模拟方法的可行性。而数值模拟中则以大尺寸壁板开展研究,壁板尺寸被设定为1000mm×1000mm×2.5mm,材料仍是304不锈钢。构建有限元模型,模型构建使用壳单元,网格划分的近似全局尺寸为15,材料参数的设定与屈曲试验一致,采用 DS4传热壳单元模拟温度场,用S4R减缩积分壳单元模拟应力应变场。施加不同的边界条件构建两种具有不同力学约束条件的模型,分别为对边约束条件(另两边自由)和四边约束条件,每种条件下又分为固支约束(固定位移和转角)和简支约束(固定位移,转角自由),如图8所示。4种情况的加载过程相同,均通过左右夹持边向面内平行推进以模拟单向压缩,随后产生屈曲现象。
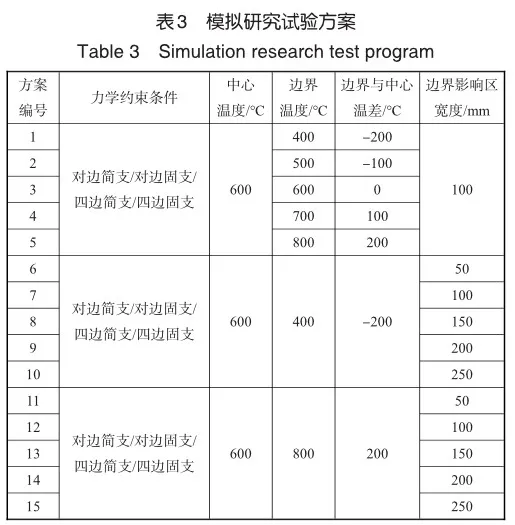
受限于喷火枪加热方式,故在试验中采用的是点加热方式。而高速航空器在飞行中发生的升温现象更接近于区域整体加热,因此在模拟研究中采用方形加热方式,使中心区域的温度呈方形分布,并留出一定的边界温度影响区,如图9所示,其中L表示方板的面内尺寸,T1表示壁板内部温度,T2表示边界温度,两者之间宽度为b的区域为边界温度影响区。模拟研究方案见表3,共分成两类:一类探究不同力学约束条件下壁板边界和内部存在不同温差时对屈曲结果的影响(试验1~5);另一类探究不同位移约束条件下边界温度影响区(即中心温度区与边界温度区间的过渡温度区)大小对屈曲结果的影响(试验6~15)。其中我们分别考虑了负温差(边界温度低于中心温度)和正温差(边界温度低于中心温度)的情况。

2.3 模拟结果与讨论
2.3.1 边界温差对屈曲的影响
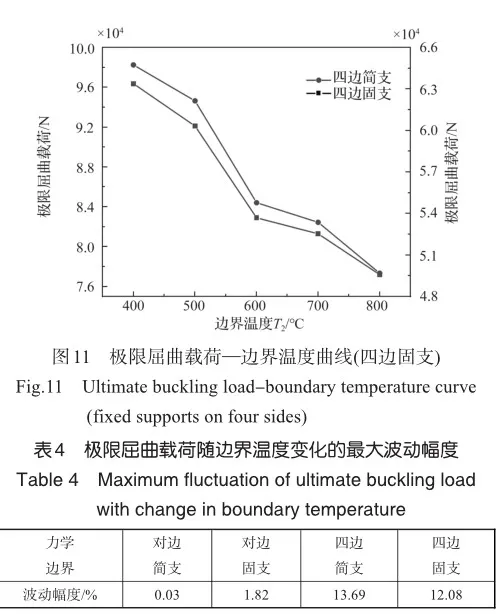
图10给出了不同边界温度下的极限屈曲载荷图。在对边约束下,壁板极限屈曲载荷受边界温度的影响不大。而在四边约束下,随着边界温度的升高,极限屈曲载荷明显下降。图11给出了四边约束下的极限屈曲载荷-边界温度曲线,可以看出负温差条件下(边界温度400~600℃)的曲线段比正温差条件下(边界温度600~800℃)的曲线段更陡,这表明壁板的极限屈曲载荷受负温差的影响大于正温差。表4给出了极限屈曲载荷随边界温度变化的最大波动幅度,可知对边约束的载荷变化小于2%,而四边约束的载荷变化大于10%,这表明四边约束下壁板热屈曲行为对边界温度的敏感性要大于对边约束情况。

2.3.2 边界温度影响区大小对屈曲的影响
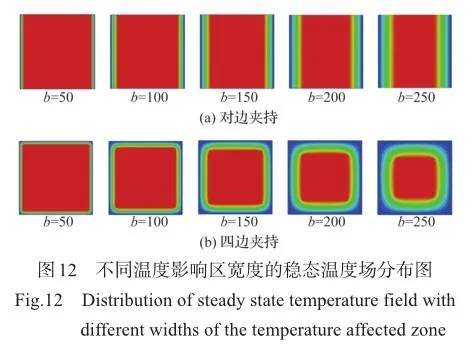
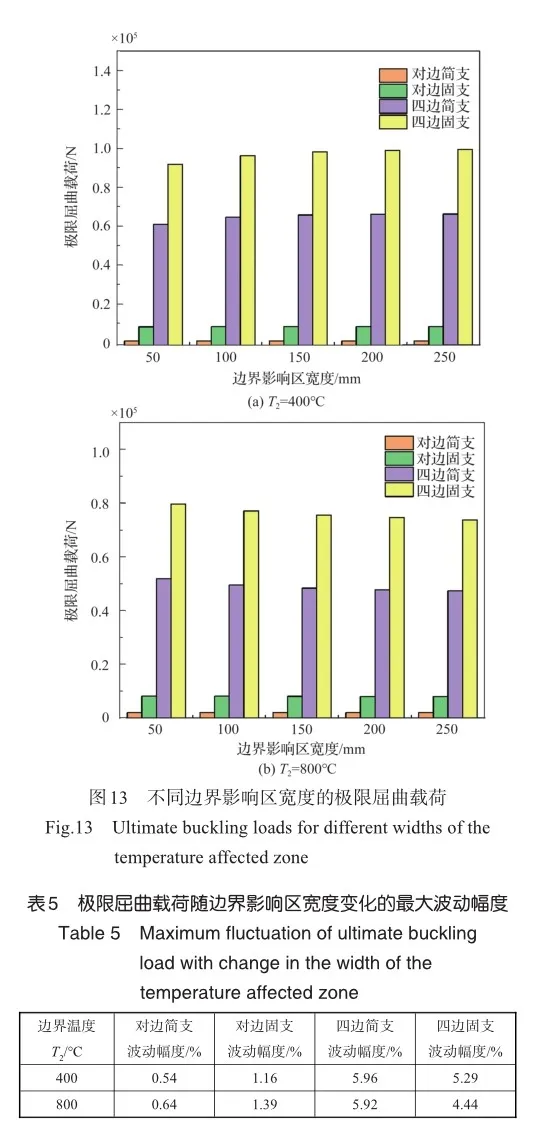
图12给出的是不同温度影响区宽度的稳态温度场,可以看出随着影响区宽度增大,中心和边界之间的温度过渡更加平缓。图13给出了不同边界影响区宽度的极限屈曲载荷图,结合表5可以看出,在对边约束下,边界温度为400℃或800℃时,影响区宽度的改变均不会对极限屈曲载荷造成明显影响(极限屈曲载荷变化均小于1.5%);在四边约束下,边界温度为400℃时影响区宽度的增大使极限屈曲载荷略微增大(极限屈曲载荷变化接近5%),而边界温度是800℃时影响区宽度的增大使极限屈曲载荷略微减小(极限屈曲载荷变化接近5%)。
3 结论
本文以平面壁板为研究对象,通过热屈曲试验以及有限元数值模拟,研究了温度边界条件对壁板结构热屈曲问题的影响规律。主要结论如下:
(1)通过平板热屈曲试验和数模模拟结果对比表明,基于热力顺序耦合方式的静力弧长法可以给出平板热屈曲行为的合理预测。
(2)边界与内部存在温差时会明显影响壁板的屈曲行为,提高平面壁板的边界温度会导致其极限屈曲载荷降低,壁板的抗屈曲能力下降;且壁板极限屈曲载荷在负温差下的影响程度比正温差条件下更大,即对低温边界更加敏感。此外,上述影响程度与边界的力学约束相关,四边约束(简支或固支)条件下内外温差的影响较显著,而对边约束条件下内外温差影响相对不敏感。
(3)相较于边界温差,边界温度影响区宽度对壁板屈曲行为的影响更小。
参考文献
[1]任青梅. 高超声速飞行器薄壁结构热屈曲行为研究进展[J].飞航导弹, 2018(7): 6-12. Ren Qingmei. Research progress on thermal buckling behavior of thin-walled structures for hypersonic vehicles[J]. Aircraft Missile, 2018(7): 6-12. (in Chinese)
[2]杨智春, 刘丽媛, 王晓晨. 高超声速飞行器受热壁板的气动弹性声振分析[J]. 航空学报, 2016, 37(12): 3578-3587. Yang Zhichun, Liu Liyuan, Wang Xiaochen. Analysis of aero‐elastic vibro-acoustic response for heated panel of hypersonic vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(12): 3578-3587. (in Chinese)
[3]Dhainaut J M, Mei C. Nonlinear response and fatigue life of isotropic panels subjected to nonwhite noise[J]. Journal of Aircraft, 2006, 43(4): 975-979.
[4]陈铁云, 沈惠申. 结构的屈曲[M]. 上海: 上海科学技术文献出版社, 1993. Chen Tieyun, Shen Huishen. Buckling of structures[M]. Shanghai: Shanghai Science and Technology Literature Publishing House, 1993. (in Chinese)
[5]孙家斌. Donnell圆柱壳屈曲问题中的辛方法[D]. 大连: 大连理工大学, 2013. Sun Jiabin. A symplectic method in buckling of Donnell’s cylindrical shells[D]. Dalian: Dalian University of Technology, 2013. (in Chinese)
[6]侯瑞, 把余炜.vYmYkiz22rKgScIpk9pme8pJ32yRjmvjvtXqMGr6xaQ= 一种复合材料翼梁后屈曲计算方法[J]. 航空科学技术, 2014, 25(12): 21-25. Hou Rui, Ba Yuwei. Post buckling calculation research on composite wing spar[J]. Aeronautical Science & Technology, 2014, 25(12): 21-25. (in Chinese)
[7]Hutchinson J W. Knockdown factors for buckling of cylindrical and spherical shells subject to reduced biaxial membrane stress[J]. International Journal of Solids and Structures, 2010, 47(10): 1443-1448.
[8]Virot E, Kreilos T, Schneider T M, et al. Stability landscape of shell buckling[J]. Physical Review Letters, 2017, 119(22): 224101.
[9]马良, 马玉娥, 秦强. 热力耦合下不同加筋壁板稳定性分析[J]. 西北工业大学学报, 2020, 38(1): 40-47. Ma Liang, Ma Yu’e, Qin Qiang. Stability analysis of different stiffened plates in thermal-mechanical coupling environments[J]. Journal of Northwestern Polytechnical University, 2020, 38(1): 40-47. (in Chinese)
[10]杨志斌, 成竹, 李丽霞,等. 一种一体化热防护承力结构的设计研究[J]. 应用力学学报, 2018, 35(4): 783-789+932. Yang Zhibin, Cheng Zhu, Li Lixia, et al. Research on a loadcarrying capacity structure design of integrated thermal protection systems[J]. Journal of Applied Mechanics, 2018, 35(4): 783-789+932. (in Chinese)
[11]杨志斌, 秦强, 曲林锋. 平板加热虚拟实验[J]. 工程与实验, 2016, 56(3): 26-29+82. Yang Zhibin, Qin Qiang, Qu Linfeng. Virtual experiment of plate heating[J]. Engineering and Experiment, 2016, 56(3): 26-29+82. (in Chinese)
[12]邓文亮, 成竹, 吴敬涛,等. 约束方式对温度环境下复材/金属混合结构壁板稳定性的影响[J]. 应用力学学报, 2020, 37(4): 1798-1804+1877. Deng Wenliang, Cheng Zhu, Wu Jingtao, et al. Effect of constraint method on stability of hybrid composite metal structural walls in temperature environment[J]. Journal of Applied Mechanics58B5cdqxO3sVRLQyk9H8W72CZ/lKSW7Ck2h/fmzzmU=s, 2020, 37(4): 1798-1804+1877. (in Chinese)
[13]屈佑文, 安效民, 邓斌,等. 热环境下复合材料壁板的非线性颤振特性分析[J]. 航空兵器, 2022, 29(4): 91-99. Qu Youwen, An Xiaomin, Deng Bin, et al. Nonlinear flutter analysis of composite panels in thermal environment[J]. Aerospace Weapons, 2022, 29(4): 91-99. (in Chinese)
[14]Rolfes R, Tessmer J, Rohwer K. Models and tools for heat transfer, thermal stresses, and stability of composite aerospace structures[J]. Journal of Thermal Stresses, 2003, 26(6): 641-670.
[15]Zhang Tianyin, Li Dongqing, Xu Tianjiao, et al. Local buckling-induced forming method to produce metal bellows[J]. Chinese Journal of Mechanical Engineering, 2023, 36(1):120-130.
[16]刘斌, 曹立阳, 王波,等. 基于多线性本构与损伤耦合的叠层陶瓷基复合材料数值预测方法[J]. 航空科学技术, 2023, 34(6): 54-65. Liu Bin, Cao Liyang, Wang Bo, et al. Numerical prediction meth‐od of laminated ceramic matrix composite based on the multilin‐ear constitutive and the coupling of damage[J]. Aeronautical Sci‐ence & Technology, 2023, 34(6): 54-65. (in Chinese)
[17]苏雁飞, 赵占文, 薛应举. 轴压载荷下复合材料薄壁加筋板后屈曲承载能力分析与试验验证[J]. 航空科学技术, 2014, 25(12): 26-29. Su Yanfei, Zhao Zhanwen, Xue Yingju. Post-buckling study and test verification of thin-walled composite stiffened panel under compression load[J]. Aeronautical Science & Technology, 2014, 25(12): 26-29. (in Chinese)
[18]任青梅. 热/力联合作用下壁板结构相似准则研究[J]. 航空科学技术, 2019, 30(8): 41-48. Ren Qingmei. Study on the similarity criterion of panel under the combined effect of temperature and static load[J]. Aeronautical Science & Technology, 2019, 30(8): 41-48. (in Chinese)
[19]卫原平, 阮雪榆. 金属成形过程中热力耦合分析技术的研究[J]. 塑性工程学报, 1994(2): 3-10. Wei Yuanping, Ruan Xueyu. A study on thermal-mechanical coupled analysis technigue of metal forming processes[J]. Journal of Plasticity Engineering, 1994(2): 3-10. (in Chinese)
[20]Hellweg H, Cris M A. A new arc-length method for handling sharp snap-backs[J]. Computers & Structures, 1998, 66(5): 705-709.
Study on the Influence of Temperature Boundary Conditions on the Buckling Phenomenon of Panels
Ding Zehang, Zhang Tianyin, Han Xianhong
Shanghai Jiao Tong University, Shanghai 200030, China
Abstract: High-speed aircraft represented by hypersonic aircraft is prone to buckling instability of the panel structure during flight, which is closely related to the thermal effect, thus the temperature boundary conditions will have an impact on the buckling behavior of the structure. In this paper, the influence of different temperature boundary conditions on the buckling behavior of the panel was studied by a set of self-designed test fixture and the static arc length algorithm based on the thermal sequential coupling method. The results show that the boundary temperature significantly affects the ultimate buckling load, and the degree of influence is related to the mechanical boundary conditions; when there is a negative temperature difference between the boundary and the domain (the boundary temperature is lower than the domain temperature), the sensitivity of the temperature effect is higher; in contrast, the width of the boundary temperature affected zone has little effect on the buckling behavior of the panel. This study can provide some reference basis for the in-depth study of thermal buckling behavior of complex panel structure.
Key Words: panel buckling; thermodynamic coupling boundary; arc length method; boundary temperature; ultimate buckling load

