基于优化RRT算法的智能车辆路径规划策略





摘要:为了解决快速搜索随机树(RRT)算法存在收敛速度慢、生成路径质量差等问题,提出一种融合算法,即将人工势场法以及A*算法的代价函数融合到RRT算法中。使用改进后的RRT算法生成路径,并将其所搜寻到的路径作为初始解传递给A*算法,进而重新规划出一条更优路径,并结合车辆运动学约束,利用贝塞尔曲线平滑路径。选取两种地图场景进行仿真实验,实验结果表明,提出的改进策略可以更快地生成质量更高且更符合汽车实际行驶的路径。仿真结果证明了该算法能有效提升RRT算法的收敛速度和路径质量。
关键词:RRT算法;人工势场法;A*算法;贝塞尔曲线
中图分类号:TP242.6文献标志码:A
0引言(Introduction)
路径规划一直是汽车自动驾驶领域的研究重点,它在自动驾驶中的作用是实现具体的行程调度[1]。目前,针对路径规划已有很多成熟的算法,常见的算法有Dijkstra算法[2]、A*算法[3]、遗传算法[4]、人工势场法[5]、RRT算法[6]等。其中,RRT算法的核心思想是通过随机扩展树结构,快速地探索搜索空间以达到搜寻路径的目的。RRT算法可以在高维空间中进行路径规划,并且适用于复杂的环境,但由于其搜索本质具有随机性,它仅能确保尽快找到路径,却难以生成最优的路径[7],因此大量学者对RRT算法进行了深入研究,例如,叶鸿达等[8]提出了一种基于A*引导的RRT算法,A*可以很好地引导RRT算法中随机树的生长,但是A*对地图的要求过于严格,因此难以用于实际。李金良等[9]提出了安全场的概念,并且结合实车的测试数据,基于距离建立安全场,对RRT算法进行改进,提高了搜索的效率和成功率,但该算法的性能在很大程度上依赖于所用数据且鲁棒性不高。
针对经典RRT算法存在的问题,结合现有学者的部分研究成果,本研究对随机点的生成添加两个生成代价,一个是A*算法的综合代价值,另一个是人工势场法的合力。只有当新节点满足这两个判定指标时,才会减少生成的冗余节点并加快收敛速度。将生成的初始路径传递给A*算法,重新搜索一条更优的路径,过滤掉多余的枝条,使最终生成的路径更优。结合车辆运动学约束,利用贝塞尔曲线平滑路径,3c521f991f288277348d9b4d54591c06最终得到一条更加符合实际的车辆行驶路径。
1经典RRT算法(ClassicalRRTalgorithm)
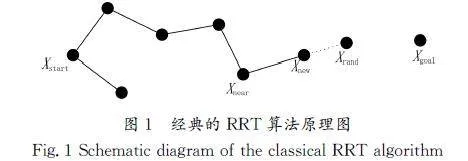
经典的RRT算法原理如图1所示。传统的RRT算法的逻辑是从初始位置Xstart出发,通过在状态空间中随机采样的方式增加新的节点,绕过在状态空间中的障碍物,当新生成的节点是目标点Xgoal或者出现在目标区域内时,最终生成一个随机树。进入循环之后,有以下几个步骤[6]。
Step1:在状态空间中随机采集节点Xrand。
Step2:查找节点集合T中距离Xrand最近的节点Xnear。
Step3:令Xnear沿着指向Xrand的方向,生长规定步长得到新节点Xnew。
Step4:对Xnear与Xnew的连线进行碰撞检测,若发生碰撞,则进行下一轮循环,若没有发生碰撞,则将新节点Xnew放入节点集合T中7565a70e5237ea09bcde0620522fda68,并且设置Xnear为Xnew的父节点。
[JP3]Step5:若Xnew等于Xgoal,或者Xnew到Xgoal的距离小于设定的阈值(即新节点到达目标范围),则路径成功找到,即退出循环。
按照RRT算法的逻辑,影响生成路径好坏的主要因素是随机点的生成与否,而随机点的生成通常是毫无规律的,大部分情况都需要较大的计算量完成路径搜索,因此想生成最优的路径十分困难,所以需要对生成的路径进行优化。
2优化RRT算法(OptimizetheRRTalgorithm)
针对RRT算法的收敛速度慢、冗余节点多的问题,提出一种基于人工势场法和A*算法的判定随机节点生成策略,当且仅当随机点满足约束条件时,才会生成,使得随机点的生成在具有较强启发性的同时,还能在遇到某些特定场景时保持其本身的随机性,并将RRT算法生成的路径作为A*算法的初始解,再利用A*算法生成一条更加合理的路径。由于在RRT算法中已经计算过初始解中节点的代价值,因此A*算法不需要重复计算。对于A*算法生成后的路径,利用贝塞尔曲线进行路径优化,在此基础上结合车辆运动学约束,使得生成的路径不仅更优且符合汽车的实际行驶路径,最终得到一条质量较高的路径。
经典的RRT算法在附近一片区域内随机选择一个点并按照步长进行扩展,即随机点的生成完全是由随机点所处的位置决定的,没有任何的约束,具备较大的随机性。这样会导致随机树生长盲目,产生很多无意义的节点。基于此问题,可以利用A*算法中的代价函数和人工势场法中的势场所产生的力对随机点的生成进行判定和限制,减少冗余节点的生成,并且缩短迭代的时间。
根据A*算法中代价函数的计算方法,F(n)为节点n的综合优先级,G(n)是起点距离当前节点n的代价,H(n)是当前节点n到终点的预计代价[3]。图3表示将综合优先级作为随机点生成的判定条件之一,对新生成的随机点进行代价检测,选择使用综合优先级F(n)小于其父节点值加上一个步长距离的点作为扩展点。这里G(n)是步长与当前路径上所生成随机点个数的乘积,具体为图3中的实线。其中预计代价H(n)的计算方法有很多,为了保证RRT算法中节点生成具有随机性,选择使用能够向任何方向生长的欧几里得距离,为图3中的长短虚线。当随机点Xrand2的综合代价大于其父节点加上一个步长的距离,即h2大于h1,则舍弃该点。
根据人工势场法的基本思想,在障碍物周围构建障碍物斥力势场,在目标点周围构建引力势场,类似于物理学中的电磁场。被控对象在这两组势场组成的复合场中受到斥力作用和引力作用,引力和斥力的合力指引着被控对象运动,搜索出无碰撞的避障路径[10]。但是,处于势场中的被控对象可能会陷入局部最小值从而导致方向不明确和路径生成失败的情况,所以需要对人工势场法的函数做一部分的修改和完善。引力计算公式如下:
Fatt(q)=-η[WTHX]ρ[WTBX](q,qg)[JZ)][JY](1)
其中:η为正比例增益系数,[WTHX]ρ[WTBX](q,qg)是一个矢量,表示从当前点到目标点的距离,方向为从当前位置指向目标点位置。斥力计算公式如下:
Freq(q)=〖JB({〗〖HL(2:1,Z;2,Z〗k[JB((]〖SX(〗1〖〗[WTHX]ρ[WTBX](q,q0)〖SX)〗-〖SX(〗1〖〗[WTHX]ρ[WTBX]0〖SX)〗[JB))]〖SX(〗1〖〗[WTHX]ρ[WTBX]2(q,q0)〖SX)〗,〖〗0≤[WTHX]ρ[WTBX](q,q0)≤[WTHX]ρ[WTBX]0
0,〖〗[WTHX]ρ[WTBX](q,q0)≥[WTHX]ρ[WTBX]0〖HL)〗〖JB)〗[JZ)][JY](2)
其中:k为正比例系数,[WTHX]ρ[WTBX](q,q0)是一个矢量,方向是从障碍物指向当前点的位置,表示的是当前点到障碍物的距离。障碍物产生斥力的条件是当前点在障碍物的影响区域内,若当前点与障碍物的距离大于设定阈值,则不产生斥力。当前位置所受到的合力,即引力与斥力之和。现添加一个斥力,即遇到目标不可达的情况时,添加一个由车辆指向目标点方向上的力,让斥力的受力方向发生改变,等于变相地增加引力而削减斥力。修改后的斥力计算公式如下:
将修改后的斥力计算公式与引力计算公式相加就是当前所受的力,此时不考虑力的方向,仅考虑其大小。如图4所示,若新的随机点受到的合力大于其父节点,则舍弃。
2.2利用A*算法进行优化路径
RRT算法是一种用于搜索无向环境中连续状态空间中路径的随机算法,与之相比,A*算法是一种启发式算法,主要用于在图中找到从起点到终点的最佳路径。因此,可以将RRT算法作为A*算法的初始解,然后通过A*算法对RRT算法生成的路径进行进一步优化。这样做的目的在于利用了RRT算法可以在复杂环境中快速生成近似路径的优势,而A*算法可以在这条路径的基础上进行更精确的优化,将两个算法的优势有机结合,带来更有效的路径规划解决方案。核心策略为在栅格化地图之后,使用A*算法对RRT算法生成的初始解进行进一步搜索,A*算法会在给定的搜索空间中基于启发式信息和路径代价评估函数,尽可能地找到最佳路径。一旦A*算法完成搜索,得到了一条路径之后,就可以删除那些冗余的枝条而只留下A*算法找到的路径,然后对这条路径进行处理。
A*算法的主要策略如下。
Step1:初始化open_list和close_list,并将RRT算法搜索到的初始路径传入open_list中。
Step2:遍历open_list,若其不为空,从其中选择优先级最高的点n,判断节点n是否为终点,若是终点,则进入Step5,若不是,则进入Step3。
Step3:将节点n从open_list中删除,并加入close_list中,遍历其附近节点,判断附近节点m是否在close_list中,若在其中,则选取下一个附近节点,若不在其中,则进入Step4。
Step4:若附近节点m也不在open_list中时,则设置节点m的父节点为节点n,并计算节点m的代价值,添加到open_list中回到Step2。
Step5:回溯路径并输出。
2.3贝塞尔曲线平滑路径
贝塞尔曲线是一种数学曲线,常用于图形设计和计算机图形学中,它的作用是在A*算法搜寻到路径之后,将离散的路径点连接,从而获得更加平滑的路径。贝塞尔曲线可以使用n个控制点{P1,P2,…,Pn}控制曲线的形状,曲线经过起点P1和终点Pn,但不经过中间点P2~Pn-1[11]。这里将A*算法搜寻到的所有路径点,按照每3个为一组,组成若干个二阶贝塞尔曲线。在二阶贝塞尔之后继续递归得到n阶贝塞尔的公式,进而一次性将所有的路径点都考虑进去。其中,贝塞尔曲线的公式如下:
p(t)=∑〖DD(〗n〖〗i=0〖DD)〗PiBi,n(t),0≤t≤1[JZ)][JY](4)
[JB({]Bi,n(t)=Cini(1-t)n-i
Cin=〖SX(〗n!〖〗i!(n-i)!〖SX)〗[JB)](i=0,1,…,n)[JZ)][JY](5)
二阶贝塞尔曲线公式如下:
B(t)=(1-t)2P0+2t(1-t)P1+t2P2,t∈[0,1][JZ)][JY](6)
2.4融合车辆运动学的约束函数
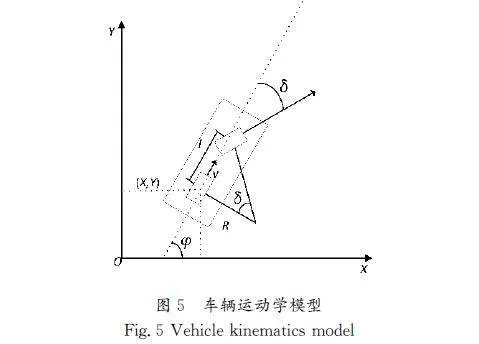
在生成的路径中,会出现有一部分位置的曲率小于汽车的最小转弯半径所要求的最小值,所以需要对生成后的路径进行约束,使路径满足车辆转向特性要求。假设车辆在平面内做匀速运动且车辆做纯滚动式运动,在任何行驶时段,车辆的速度都一定指向纵轴的垂直方向。将车辆简化为二自由度的自行车模型,如图5所示,l是轴距,φ是横摆角,δ是车辆前轮转角,(X,Y)是后轴轴心坐标。为了验证优化算法的可行性,在VisualStudio2022中进行算法的仿真验证。为了验证其改进效果,将经典RRT算法、基于密集节点过滤的RRT算法与本文算法布置在同一张地图上进行仿真实验,简单场景下的仿真结果如图6所示,复杂场景下的仿真结果如图7所示。将引力系数设为0.5,斥力系数设为0.5,RRT扩展步长设为50。设置两种地图场景,一种简单、一种复杂,地图大小均为750×750。图6、图7中较细的线条为搜寻后生长的枝条,其中加粗的线条为生成的最终路径。
由图6、图7可知,经典RRT算法的路径分支繁多,难以快速地找到路径,而基于密集节点过滤的RRT算法能有效地减少分支。本文提出的改进RRT算法可以很好地避免多分支情况的出现,还可以在保留经典RRT采样随机性的同时,给予随机点较强的目标启发性,并且减少搜索时间和缩短路径长度,同时更加符合车辆的运动学规律。根据生成的最终曲线,可以确定路径的质量也得到了提高。为了确保算法的科学性,本研究分别在简单场景下和复杂场景下,对表1中的3种算法进行了100次仿真实验,具体的实验结果分别如表1和表2所示。
通过表1和表2,可以很明显看出,不管是在简单场景还是复杂场景中,本文算法的路径规划时间、路径长度、所生成的随机点的个数均是最少的。并且相比于密集节点过滤的RRT算法,本文算法在简单场景中的规划速度提升了62%左右,随机点减少了50%左右;在复杂场景中的规划速度提升了51%左右,随机点减少了57%左右。此外,在使用贝塞尔曲线平滑路径后,路径长度得到明显缩短。
4结论(Conclusion)
基于智能车辆的路径规划算法的研究中,本文对于RRT算法、A*算法、人工势场法进行了深入研究,通过仿真实验,揭示了经典RRT算法存在的问题,包括冗余节点多、随机点生成无规律及生成路径质量差等。为了解决以上问题,首先在RRT算法中融合人工势场法和A*算法,明显减少了迭代的次数和迭代所需要的时间,生成的随机点具备一定的方向性;其次通过A*算法生成了一条质量更高的路径,并利用贝塞尔曲线平滑路径;最后对所生成路径进行车辆运动学约束,使生成的路径更加满足车辆的实际行驶要求。经过大量的仿真实验,证明了优化后RRT算法具有一定的可行性和科学性。
参考文献(References)
[1]采国顺,刘昊吉,冯吉伟,等.智能汽车的运动规划与控制研究综述[J].汽车安全与节能学报,2021,12(3):279\|297.
[2]马新国,马希青.融合改进RRT和Dijkstra算法的机器人动态路径规划[J].组合机床与自动化加工技术,2023(2):5\|9.
[3]郭昭烽,谢玲,刘红英,等.移动机器人路径规划算法仿真及实现[J].软件工程,2022,25(4):25\|29.
[4]孙俊丽.谈遗传算法[J].办公自动化,2019,24(12):48\|49.
[5]LIUJ,QINXL,QIBL,eta1.3DonlinepathplanningofUAVbasedonimproveddifferentialevolutionandmodelpredictivecontrol[J].Internationaljournalofinnovativecomputing,informationandcontrol,2020,16(1):315\|329.
[6]笪晨,宋天麟,施维.多策略模式下RRT算法的优化[J].组合机床与自动化加工技术,2022(12):128\|131,135.
[7]谭波,罗均,罗雨松,等.改进Ra5bf9f4dd2099b8e75e23f4d9e0cbf8cb097d00314a12c82d2abccb1a86fa2bfRT算法的机器人路径规划[J].重庆大学学报,2023,46(9):13\|22.
[8]叶鸿达,黄山,涂海燕.基于改进Bi\|RRT*算法的移动机器人路径规划[J].电光与控制,2022,29(2):76\|81.
[9]李金良,舒翰儒,刘德建,等.基于改进RRT路径规划算法[J].组合机床与自动化加工技术,2021(2):22\|24,29.
[10]PANGBZ,DAIW,HUXT,etal.Multipleairroutecrossingwaypointsoptimizationviaartificialpotentialfieldmethod[J].Chinesejournalofaeronautics,2021,34(4):279\|292.
[11]韩浩,王舜燕.基于混合贝塞尔曲线模型的车道检测算法[J].计算机工程与设计,2018,39(3):732\|737.

