融合翻筋斗觅食和正余弦策略的白骨顶鸡优化算法
摘要:针对白骨顶鸡优化算法(COOT)全局搜索能力差、优化精度低和易陷入局部最优等缺陷,提出了一种融合翻筋斗觅食和正余弦策略的白骨顶鸡优化算法,引入一种翻筋斗觅食策略,增加了白骨顶鸡个体的多样性。此外,在领导者位置更新过程中采用正余弦策略和随机因子,以提高算法的搜索能力。通过10个标准检验函数,以及Wilcoxon秩和检验,对改进的COOT性能进行了全面评估,并将其与其他几种算法进行了比较。仿真结果表明,改进的COOT在迭代速度和收敛精度方面取得了显著的提升,并展现了出色的鲁棒性。
关键词:改进白骨顶鸡优化算法;翻筋斗觅食策略;正余弦策略;随机因子
中图分类号:TP301.6文献标志码:A
0引言(Introduction)
近年来,深度学习以及智能优化算法成为解决工程应用或管理领域中复杂任务问题的有力工具[1\|2]。随着人工智能的兴起,智能优化算法的研究与应用更显得尤为重要。白骨顶鸡优化算法(CootOptimizationAlgorithm,COOT)是NARUEI等[3]在2021年提出的一种新型智能优化算法,通过模仿白骨顶鸡的运动习性,包括其在水上游动时的协调性、快速转向能力和在复杂环境中的灵活性。COOT具有简明易懂、易于实施的特点,并且拥有出色的全局优化能力。尽管COOT已经在某些工程优化问题中展现了其应用价值并得到了成功应用[4],但是仍然存在与其他智能优化算法相同的搜索能力不足和易陷入局部最优等问题[5]。目前,许多学者引入了多种策略以期改进其性能。例如,MEMARZADEH等[6]为了优化风电功率预测模型的参数,提出了一种基于长短期记忆和白骨顶鸡优化算法的风力发电企业新型最优储能系统模型。同样,DIAB等[7]为了准确估计各种光伏模型,使用平衡白骨顶鸡优化算法和人工生态系统优化算法对光伏模型参数进行优化。GOUDA等[8]为了优化太阳能机组在各种运行和负载场景下的性能,提出了基于白骨顶鸡优化算法的太阳能发电机组的性能评估。
针对COOT的缺陷,本文提出融合翻筋斗觅食和正余弦策略的白骨顶鸡优化算法(SSFCOOT)。首先,通过白骨顶鸡个体的翻筋斗觅食策略,使算法跳入新的位置,扩大了搜索范围并避免陷入局部最优解。其次,在领导者位置更新中引入正余弦策略,并通过随机因子对正余弦算法进行改进,以加快收敛速度和增强算法的搜索能力。
1白骨顶鸡优化算法(CootOptimizationAlgorithm)
COOT借鉴了白骨顶鸡群在水面上的移动习性,主要有4种不同的运动行为,分别是个体随机运动、链式运动、跟随领导者移动和领导者移动。
1.1初始化种群
根据公式(1)随机初始化白骨顶鸡种群位置:
CootPos(i)=rand(1,d)×(ub-lb)+lb[JZ)][JY](1)
其中:CootPos(i)是第i个白骨顶鸡的位置,rand为0到1的随机数,d表示维度,ub和lb分别是搜索空间的上限和下限。ub和lb的定义分别如公式(2)和公式(3)所示:3eKiJMxWVv3SPbbioq9Yvg==
ub=[ub1,ub2,…,ubd][JZ)][JY](2)
lb=[lb1,lb2,…,lbd][JZ)][JY](3)
初始化种群后,根据以下4种运动行为更新白骨顶鸡的位置。
1.2个体随机运动
在个体随机运动中,使用公式(4)随机初始化位置Q:
Q=rand(1,d)×(ub-lb)+lb[JZ)][JY](4)
个体随机运动探索了搜索空间的不同部分。为了避免陷入局部最优,根据公式(5)更新位置:
CootPos(i)=CootPos(i)+A×R2×(Q-CootPos(i))[JZ)][JY](5)
其中:R2为[0,1]区间中的随机数,A是迭代的随机函数,更新方式如下:
A=1-L×〖SX(〗1〖〗Iter〖SX)〗[JZ)][JY](6)
其中:L为当前的迭代次数,Iter为最大的迭代次数。
1.3链式运动
链式运动通过使用两个个体的平均位置实现。首先计算两个个体之间的距离向量,其次将其中的一个个体向另一个个体移动大约距离向量的一半,个体的新位置如下:
CootPos(i)=0.5×(CootPos(i-1)+CootPos(i))[JZ)][JY](7)
其中,CootPos(i)是第二个个体。
1.4跟随领导者移动
白骨顶鸡根据小组中领导者的位置更新自己的位置,每组中的白骨顶鸡跟随者向领导者移动。领导者的选择如公式(8)所示:
K=1+(iMODNL)[JZ)][JY](8)
其中:i是当前个体的位置索引,NL是领导者的数量,K表示选定的第K个领导者。个体的位置更新如下:
[JZ]CootPos(i)=[WB]LeaderPos(k)+2×R1×cos(2Rπ)×
[DW](LeaderPos(k)-CootPos(i))[JY](9)
其中:CootPos(i)是个体的当前位置,LeaderPos(k)是选中的领导者位置,R1是[0,1]区间中的随机数,R是[-1,1]区间中的随机数。
1.5领导者移动
为了找到最优位置,领导者必须从现有的局部最优位置跳转到全局最优位置。利用公式(10)更新领导者的位置。
LeaderPos(i)=〖JB({〗B×R3×cos(2Rπ)×(gBest-
LeaderPos(i))+gBest,R4<0.5
B×R3×cos(2Rπ)×(gBest-
LeaderPos(i))-gBest,R4≥0.5〖JB)〗[JY](10)
其中:gBest为领导者种群内最优个体的位置,R3和R4均为[0,1]区间中的随机数,R为[-1,1]区间中的随机数,B是迭代的随机函数,其更新方式如下:
2[ZK(][JP3]融合翻筋斗觅食和正余弦策略的白骨顶鸡优化算法(CootOptimizationAlgorithmbasedonsomersaultforagingandsine\|cosinestrategy)[HJ][BT)]
2.1翻筋斗觅食策略
为了增强COOT的跳出局部最优解能力,引入了一种独特的翻筋斗觅食策略。该策略将猎物的位置视为一个支点,并通过围绕支点旋转和翻滚的方式不断寻找新的位置。翻筋斗觅食策略如公式(12)所示:
CootPos(i)=[WB]Cootpos(i)+s×(rand×gBestScore-rand×[DW]CootPos(i))[JY](12)
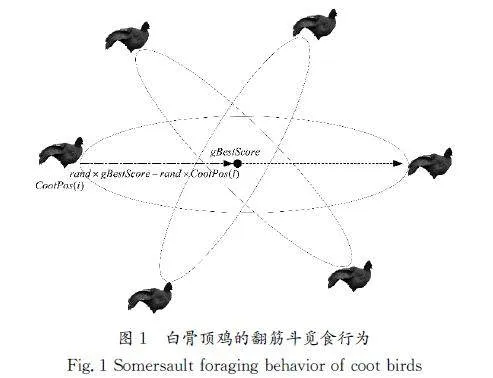
其中:CootPos(i)是白骨顶鸡跟随者的当前位置,s代表空翻因子,gBestScore表示目前的最优位置,rand为[0,1]区间中的随机数。图1为白骨顶鸡的翻筋斗觅食行为。
根据公式(12)和图1可知,白骨顶鸡的移动范围取决于当前位置与其对称位置之间的新搜索域。该搜索域是围绕迄今为止发现的最佳白骨顶鸡位置而确定的。白骨顶鸡越接近最佳位置,对当前位置的扰动就越小,使得所有个体在搜索空间中逐渐趋近最优解。因此,随着迭代次数的增加,白骨顶鸡翻筋斗觅食的范围会逐渐缩小,实现自适应的调整。
2.2正余弦策略
MIRJALILI提出了一种基于种群的优化算法,即正余弦算法[9](SCA),用于解决各种优化问题。该算法基于正弦和余弦函数的数学模型搜索空间中的不同区域,并要求它们朝着最优解振荡。为了使这一阶段的领导者群体运动更加随机,避免陷入局部优化,引入了随机因子p∈(0,1)。得到新的领导者位置更新公式如下:
LeaderPos(i)=〖JB({〗B×R3×cos(2Rπ)×(gBest-LeaderPos(i))+
p×gBest,R4<0.5
B×R3×sin(2Rπ)×(gBest-LeaderPos(i))-
p×gBest,R4≥0.5〖JB)〗[JZ)][JY](13)
2.3SSFCOOT算法步骤
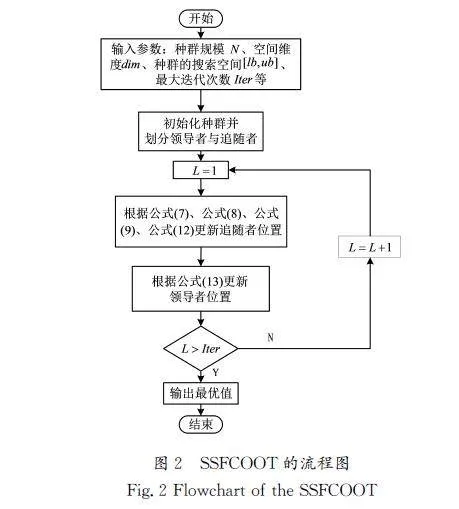
综上改进策略,本文所提的SSFCOOT,其计算步骤如下。
步骤1:初始化算法的相关参数,即种群规模N、空间维度dim、种群的搜索空间[lb,ub]、最大迭代次数Iter等。
步骤2:根据公式(1)初始化种群并划分领导者与跟随者。
步骤3:根据公式(4)随机生成位置Q。
步骤4:根据公式(7)、公式(8)、公式(9)、公式(12)更新追随者位置。
步骤5:计算追随者适应度并更新领导者。
步骤6:根据公式(13)更新领导者位置。
步骤7:计算领导者适应度。
步骤8:对迭代终止条件进行判断,若满足条件,则进行下一步操作;否则,继续执行步骤3。
3实验结果分析(Analysisofexperimentalresults)
3.1基准测试函数
为了验证本文改进算法(SSFCOOT)的寻优能力,将SSFCOOT与标准COOT、鲸鱼优化算法(WhaleOptimizationAlgorithm,WOA)[10]、蚁狮优化算法(AntLionOptimizer,ALO)[11]、阿基米德优化算法(ArchimedesOptimizationAlgorithm,AOA)[12]、海鸥优化算法(SeagullOptimizationAlgorithm,SOA)[13],分别选取5个单峰函数和5个多峰函数[14]进行对比仿真实验。此外,6种算法均采用相同的软件和硬件平台,实验是在配备32GBRAM与i7\|12700H处理器的个人计算机上进行的。
3.2收敛精度分析[HJ2.4mm]
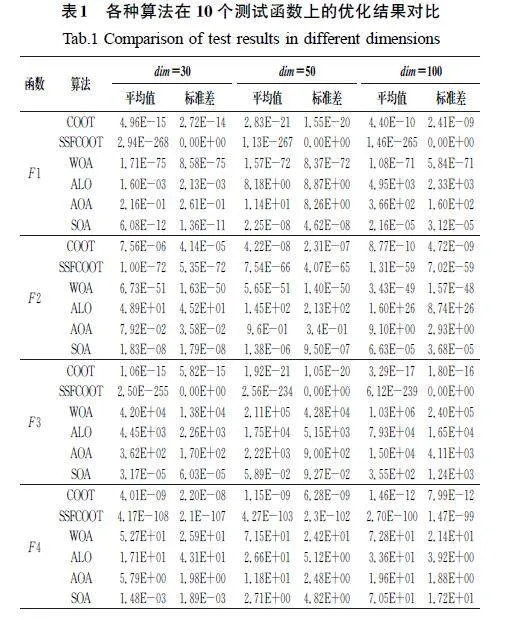
为了评估SSFCOOT的优化精度,本研究对比了改进算法与其他5种算法在10个测试函数(空间维数dim=30/50/100)上的性能。每种算法针对每个测试函数独立运行30次,并使用平均值和标准差评估它们的优化性能。表1展示了各种算法在10个测试函数上的优化结果对比。
由表1可知,从纵向来看,SSFCOOT的求解精度明显优于其他5种算法,其中ALO的求解精度是其他5种对比算法中表现最差的,AOA次之。从维度方面来看,随着测试函数维度的增加,COOT、WOA、ALO、AOA、SOA的寻优能力整体呈现下降趋势,这是因为维度增加使测试函数的复杂度增大,导致寻优过程需要更大的计算量。WOA和SSFCOOT在求解函数F6和F8时,能够准确地找到理论最优值0,显示出卓越的优化能力。对于单峰函数来说,SSFCOOT的求解精度最高,也从侧面表明了翻筋斗觅食和正余弦策略的引进提高了SSFCOOT的鲁棒性。
3.3收敛曲线分析
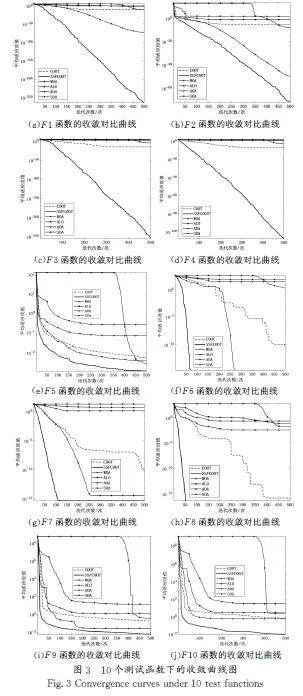
为了深入分析各种算法的收敛性能,图3展示了6种算法在10个测试函数上的收敛曲线。
如图3(a)、图3(b)、图3(c)和图3(d)中的单峰收敛曲线所示,SSFCOOT的收敛曲线一开始迅速减小,接近理论最优值,并且其收敛速度随着迭代次数的提升而提升。然而,对于其他5种算法,它们的收敛曲线呈现平缓的变化趋势,并陷入局部最优。这表明翻筋斗觅食策略可以有效地探索算法的理论最优解,防止其陷入局部最优。此外,图3(f)、图3(h)中的多峰收敛曲线表明,SSFCOOT和WOA在寻找最优值时,收敛速度非常快,并最终获得理论最优解。然而,COOT似乎处于停滞状态并陷入局部最优,验证了引入正余弦策略和随机因子可以帮助提高算法的全局优化能力。同样,如图3(e)、图3(i)和图3(j)中的收敛曲线所示,SSFCOOT、WOA、COOT和AOA都表现出良好的搜索精度,但SSFCOOT的收敛速度明显快于其他3种算法。综上,与其他5种算法相比,SSFCOOT在收敛精度和收敛速度方面都具有优势,证实了本文提出的改进方法的有效性。
3.4Wilcoxon秩和检验
为了全面评估SSFCOOT在全局寻优方面的优越性,仅凭平均值和标准差作为性能指标是不足以充分说明问题的。为了确定SSFCOOT与其他5种算法之间是否存在显著差异,本文采用Wilcoxon秩和检验进行性能测试。设定原假设H0:两种算法在寻优性能上基本相同。此外,提出了备选假设H1:两种算法在性能上存在显著差异。通过Wilcoxon秩和检验,可以更准确地评估SSFCOOT与其他算法之间的差异,以进一步验证其优越性。
当P<0.05时,可以被认为拒绝H0假设,说明两种算法在性能上存在显著差异;当P>0.05时,可以被认为接受H0假设,说明两种算法在寻优性能上基本相同。
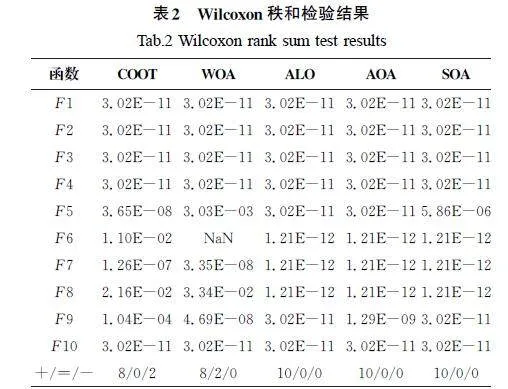
表2为10个测试函数在搜索空间维度dim=30时,独立运行30次的SSFCOOT与COOT、WOA、ALO、AOA、SOA的Wilconxon秩和检验对比分析。其中,“NaN”表示不适用,即无法进行显著性判断。“+”“=”“-”分别表示SSFCOOT的性能“优于”“相当于”“劣于”其他算法。
由表2可知,大部分P值都小于0.05,总体上SSFCOOT的性能与其他5种算法的差异显著,从而表明SSFCOOT相对于其他算法具有一定的优越性。
4结论(Conclusion)
本文提出了一种融合翻筋斗觅食和正余弦策略的白骨顶鸡优化算法(SSFCOOT),旨在找到全局最优解,提高收敛速度。首先,翻筋斗觅食策略的引入使SSFCOOT能够扩大搜索范围,增强种群多样性。其次,在领导者位置中使用正余弦策略,并引入随机因子,提高了算法的搜索能力。通过对10个基准测试函数进行的仿真实验,以及基于Wilcoxon秩和检验的性能比较,验证了SSFCOOT在收敛精度和速度方面的优越性,同时该算法表现出较小的标准偏差,具有极强的稳定性。
参考文献(References)
[1]缪晓宾,陈昊.模拟退火算法优化转运小车转向的梯形机构设计[J].机械设计与研究,2023,39(5):67\|71.
[2]杨宝杰,石凯元,陈佳凯,等.基于改进粒子群算法的电力工程数据多目标优化方法[J].电子设计工程,2024,32(5):95\|99.
[3]NARUEII,KEYNIAF.AnewoptimizationmethodbasedonCOOTbirdnaturallifemodel[J].Expertsystemswithapplications,2021,183:115352.
[4]张立峰,陈达.基于改进白骨顶鸡优化算法的ECT图像重建[J].计量学报,2023,44(11):1692\|1698.
[5]李雪利,杜逆索,欧阳智,等.基于扰动因子和贪心策略的白骨顶优化算法[J].智能计算机与应用,2023,13(6):38\|49.
[6]MEMARZADEHG,KEYNIAF.AnewoptimalenergystoragesystemmodelforwindpowerproducersbasedonlongshorttermmemoryandCootBirdSearchAlgorithm[J].Journalofenergystorage,2021,44:103401.
[7]DIABAAZ,EZZATA,RAFAATAE,etal.OptimalidentificationofmodelparametersforPVsusingequilibrium,cootbirdandartificialecosystemoptimisationalgorithms[J].IETrenewablepowergeneration,2022,16(10):2172\|2190.
[8]GOUDAEA,KOTBMF,GHONEIMSSM,etal.Performanceassessmentofsolargeneratingunitsbasedoncootbirdmetaheuristicoptimizer[J].IEEEaccess,2021,9:111616\|111632.
[9]MIRJALILIS.SCA:aSineCosineAlgorithmforsolvingoptimizationproblems[J].Knowledge\|basedsystems,2016,96:120\|133.
[10]MIRJALILIS,LEWISA.Thewhaleoptimizationalgorithm[J].Advancesinengineeringsoftware,2016,95:51\|67.
[11]MIRJALILIS.Theantlionoptimizer[J].Advancesinengineeringsoftware,2015,83:80\|98.
[12]HASHIMFA,HUSSAINK,HOUSSEINEH,etal.Archimedesoptimizationalgorithm:anewmetaheuristicalgorithmforsolvingoptimizationproblems[J].Appliedintelligence,2021,51(3):1531\|1551.
[13]DHIMANG,KUMARV.Seagulloptimizationalgorithm:theoryanditsapplicationsforlarge\|scaleindustrialengineeringproblems[J].Knowledge\|basedsystems,2019,165:169\|196.
[14]胡春安,熊昱然.多策略改进的混沌哈里斯鹰优化算法[J].计算机工程与科学,2023,45(9):1648\|1660.
作者简介:
张志飞(1999\|),男,硕士生。研究领域:智能算法,计算机视觉。
孔维宾(1990\|),男,博士,副教授。研究领域:信号处理,微波技术。本文通信作者。
杜义(2000\|),男,硕士生。研究领域:智能检测。
张婷琳(1988\|),女,博士,讲师。研究领域:信号处理,人工智能。
王玉婷(2003\|),女,本科生。研究领域:电子信息。
高薪越(2004\|),女,本科生。研究领域:电子信息。

