基于时延Petri网的大型工程机械装备排产模型与收敛算法

摘要：在大型工程机械装备的柔性制造系统中，由于涉及多个车间且存在大量的并行加工过程，因此资源被闲置浪费的情况比较常见。为解决此问题，提出一种基于时延Petri网的大型工程机械装备排产模型与收敛算法。首先，在建模过程中对各种存在并行加工的情况使用约束矩阵进行描述，利用Petri网建立系统模型，实现对车间内各机床之间调度流程的描述，并在发生突发事件时进行模型重建；其次，使用一种基于遗传算法和粒子群优化的融合算法，构建算法的适应度函数；最后，根据算法求出模型的最优路径，达到资源利用的最大化。

关键词：柔性制造系统；大型工程机械装备；Petri网；遗传算法

中图分类号：TP301.6文献标志码：A

0引言（Introduction）

Petri网已被广泛应用于众多行业。张宁等［1］针对鱼雷装备测试维修使用需求，采用广义随机Petri网模型进行测试维修建模；闫哲等［2］提出逻辑博弈概率Petri网，使用Petri网描述动态博弈过程；贾云富等［3］提出了一种适用于柔性生产线调度研究的Petri网模型，用于描述柔性生产线的调度过程；王慧英等［4］提出基于约束优化的Petri网可达性伪标识判定模型构建方法，使用该方法构建Petri网可达性伪标识判定模型时的CPU占用率低、网络路径覆盖率高、判定效果好；樊海刚等［5］基于Petri网可能出现的状态集同构马尔科夫链，实现了定量评价地震应急协同能力；徐海军等［6］则提出基于模糊Petri网的有载分接开关故障诊断模型，以解决分接开关实际发生故障与结果之间存在偏差的问题；YANG等［7］使用高级Petri网处理模糊物联网冲突策略的建模和推理；KABASHKIN等［8］利用Petri网评估环境、社会和经济方面走廊可持续性的通用方法；CUI等［9］提出了一种基于时间转移Petri网的描述模型，用于实现飞机周转时间预测。

在面对拥有大量零部件的大型工程机械装备和存在大量的并行制造过程时，传统的柔性制造系统排产模型无法很好地描述制造过程中的复杂情况。基于此，本文采用一种基于Petri网的建模方式对大型工程机械装备的柔性制造系统建立模型，通过对此模型进行求解，进而得出最优的工序路径。

1.1首次建模

柔性制造系统由各种类型的车间组成，这些车间包括锻件车间、精加工车间、焊接车间、装_{aZ0xub/B62nZfnv+CLJCTA==}配车间等，车间中又包含了用于工件工序加工的各种机床资源。基于柔性制造的特性，一个工序可以由多种机器路径实现，不同的机器有不同的加工时间。因此，在建立模型之前需要对建模流程中的变量进行统一定义，具体如下。

1.[JP3]方法charmap（int）是一种映射关系，该方法接收数字参数，将其进行唯一映射为该数字对应的一个字母，如map（1）->a，表示将数字1映射为字母a，并且a仅由1映射。

2.机器的数量为x，工件的数量为y。

3.机器集定义为集合X={Xi|i∈1，2，…，x}。

4.工件集定义为集合Y={Yi|i∈1，2，…，y}。

5.工件Xa的加工工序集定义为集合Pa={Pai|i∈1，2，…，len（Xa）}，集合中的个体Pab表示工件Xa的第b步加工工序。

6.可以实现工序Pab的机床集合定义为集合MTab={MTabi|i=1，2，…，len（MTab）}，集合中的元素MTabc表示可以完成工序Pab的第c个机床。

7.库所集合S={Si|i=1，2，…，len（S）}。

8.变迁集合T={Ti|i=1，2，…，len（T）}。

9.时延集合Delay={Di|i=1，2，…，len（D）}，表示为同一个变迁Ti发射的所有token均必须经过Di时间长度之后，才会变成可用的token。

10.系统的输入矩阵为[WTHX]IN[WTBX]（Si，Tj），表示变迁Tj发射之后，需要库所Si提供的token的数量，发射变迁Ti需要的所有token表示为∑〖DD（〗len（T）〖〗i=1〖DD）〗[WTHX]IN[WTBX]（Si，Tj），只有当变迁对应的所有输入库所的token数量不小于输入矩阵中该变迁对应的值时，变迁才是可以发射的。

11.系统的输出矩阵为[WTHX]OUT[WTBX]（Si，Tj），表示变迁Tj发射之后，输出到库所Si中的token数量，变迁Tj发射的token集合表示为∑〖DD（〗len（T）〖〗i=1〖DD）〗[WTHX]OUT[WTBX]（Si，Tj），变迁Tj发射的所有token经过Delay（Si）之后，变成可用token。

基于时延Petri网的柔性制造系统的排产模型建模算法的逻辑如下。

1.计算机器的数量为x，工件的数量为y。

2．根据机器的数量和工件的数量，建立输入矩阵[WTHX]IN、输出矩阵OUT[WTBZ]及存放中间数据的List集合。

3.遍历工件集合中的所有的工件：forYiinY（第一层循环）。

4.创建工件Yi的加工开始库所Siα，加工结束库所Siβ，加工开始变迁Tiα。

5.赋值操作：[WTHX]IN[WTBX]（Siα，Tiα）=1。

6.将变迁Tiα放入List集合中：List.add（Tiα）。

[HJ1.5mm]

7.遍历工件Yi所有的工序：forPijinPi（第二层循环）。

8.创建工序选择库所Sij。

9.遍历List集合中的所有元素while（list.iterator（）.hasNext（））。

10.赋值操作[WTHX]OUT[WTBX]（Sij，iterator（）.next（））=1。

11.List集合遍历结束后，清空集合中的所有元素：List.clear（）。

12.遍历可以完成工序Pij的所有机床集合：forMTabcinMTab（第三层循环）。

13.创建工序Pij的工序开始变迁Tijk，工序结束变迁Ti（j+1）map（k），工序加工库所Sijk。

14.赋值操作：

[WTHX]IN[WTBX]（Sij，Tijk）=1；

[WTHX]IN[WTBX]（Sij，Ti（j+1）map（k））=1；

[WTHX]IN[WTBX]（SMT，Tijk）=1；

[WTHX]OUT[WTBX]（Sijk，Tijk）=1；

[WTHX]OUT[WTBX]（SMT，Tijk）=1。

15.将工序结束变迁放入List集合中：List.add（Ti（j+1）map（k））。

16.结束第三层循环。

17.结束第二层循环。

18.遍历List集合中的所有元素while（list.iterator（）.hasNext（））。

19.赋值操作[WTHX]OUT[WTBX]（Siβ，iterator（）.next（））=1。

20.结束第一层循环。

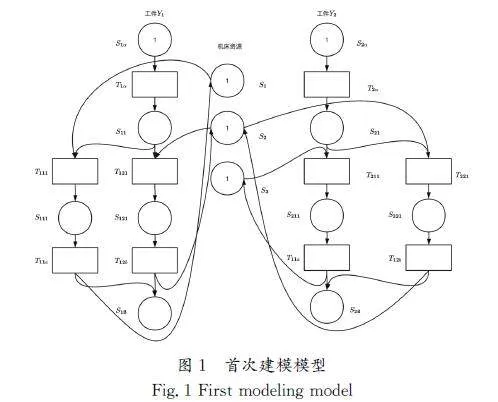
建模算法的输入为加工机床集合MT、工件集合Y及所有工件的工序集合P；建模算法的输出为变迁输入矩阵[WTHX]IN和变迁输出矩阵OUT[WTBZ]。首次建模模型如图1所示。

模型的时延特性在工序加工库所Sijk和时延集合Delay中体现，例如当变迁T121发射后，库所S121中的token必须等待Delay（S121）时间之后，才会变成可用token，因此变迁T12b不会立即使能，机器资源库所S2中token的数量在Delay（S121）时长内为0，假如此时工件2同样需要使用2号机床的变迁T221时，由于没有满足变迁发生条件的token数量，因此变迁T221不是使能的，此时工件2有两个选择，即等待变迁T12b发射，归还库所S2的token；或是选择3号机床执行变迁T211。

1.2突发事件重建模方法

在大型工程机械装备柔性制造系统运行时，可能会发生一些事件干扰当前正在进行的生产流程，比如出现加工机床故障、紧急插单等，如果不实时修改原来已经建立的排产模型，就可能产生工序错误。

基于此，提出一种针对突发事件的重建模方法，该方法可以在发生机床故障、紧急插单等突发事件时进行重新建模，并在突发事件解决后再次进行重建模，以保证最大化地利用柔性制造系统中的资源。

1.2.1安全点机制

突发事件重建模方法参考了Java虚拟机垃圾回收机制中的安全点思想：在HotSpotJava虚拟机中，对内存堆区域中的不可达对象进行垃圾回收的时机不是任意的，需要Java虚拟机进程的所有线程都执行到定义的安全点的位置后，虚拟机开始对堆中的对象进行可达性分析，标记可达对象，再对不可达对象进行回收。突发事件重建模方法同样定义了安全点机制：定义安全点集合SP={Si|i=1，2，…，len（SP）}。只有在安全点时，才可以进行重建模。

1.2.2机器故障重建模

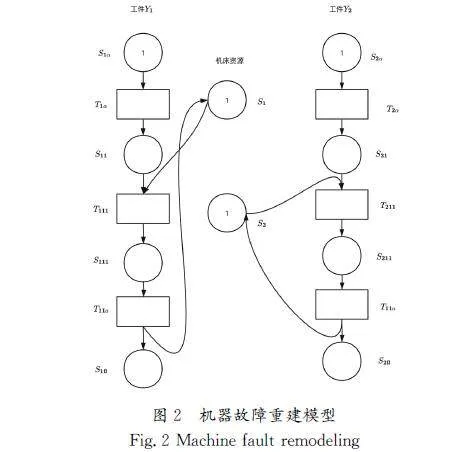
以首次建模的模型为例，当发生机器故障时，假设2号机床发生故障无法使用，此时模型的加工机床集合MT发生了变化，在安全点库所S11加入暂停逻辑，并按照上文提出的建模算法流程进行重建模操作，输入为当前可用的加工机床集合MT，工件集合Y，所有工件的工序集合P，机器故障重建模型如图2所示。

如果故障的机床在原系统模型中表示正在使用，即工序加工库所S121中的token数量不为0，则需要回退到安全点S11，然后进行重建模操作。

1.2.3紧急插单重建模

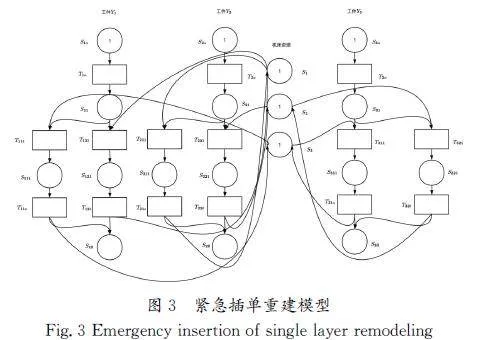
以1.1节中的模型为例，当发生紧急插单事件时，当工件Y1和工件Y2正在进行加工时，有工件Y3要紧急插单，优先级高于Y1和Y2，此时模型的工件集合Y、工件的工序集合P均发生了变化。在安全点库所S11加入暂停逻辑，并进行重建模操作，输入为按照权重排序的工件集合Y、加工机床集合MT、所有工件的工序集合P，紧急插单重建模型如图3所示。

紧急插单工件排序后，作为工件集合Y中的第一个元素Y1，原工件Y1在新工件集合中为Y2，原工件Y2在新工件集合中为Y3。同理，工件的工序集合P也相应地进行修改。

与机器故障不同，紧急插单不会进行回退操作，假设原系统工序加工库所S111中的token数量不为0，表示该工序对应的机床资源1号机床正在使用中，此时插单的工件必须等待该机床使用完毕，或者使用其他的机床完成工序。

1.2.4重建模流程

所有变量的意义已在1.1节中说明，建模算法的输入为加工机床集合MT、工件集合Y、所有工件的工序集合P、突发事件类型Type、原变迁输入矩阵[WTHX]IN和原变迁输出矩阵OUT[WTBX]、原模型上下文Context，建模算法的输出为变迁输入矩阵[WTHX]IN和变迁输出矩阵OUT[WTBX]，排产模型重建模算法逻辑如下。

本文提出一种基于遗传算法和粒子群算法的融合算法，首先使用遗传算法对解集中的个体进行选择、交叉、变异操作，将遗传算法一次迭代后生成的新种群作为粒子群优化算法的初始粒子群，计算个体极值和群体极值。其次对粒子进行随机扰动，判断此次的粒子是否更优，若更优，则更新粒子的速度和位置，并更新个体极值和群体极值。最后开始下一次遗传算法和粒子群优化算法的迭代，最终输出一个问题的最优解序列。

算法约束条件如下。

（1）根据Petri网建立的柔性排产系统的运行规则：当且仅当p∈·t，M（p）≥W（p，t）时，变迁t是有权利发生的，当变迁的发生条件可以得到满足时，从·t中转移权重函数数量的token到t·中。

（2）工序顺序规则：在柔性制造系统中进行加工的各种零部件，需要遵守事先规定的加工工序顺序。

（3）[JP3]并行加工规则：当柔性制造系统中存在并行加工操作时，需要根据融合算法给出的最终解序列，按照顺序进行工序加工。

算法输入：基于Petri网的柔性排产模型、工序约束矩阵、最大迭代次数imax、种群中的个体数量Size、交叉概率Mc和变异概率Mm。

算法输出：当前种群最短加工时间及其对应的染色体序列（加工路径）。

融合算法流程如下。

1.根据基于Petri网建立的柔性制造系统模型中变迁的数量，确定解向量的维度l，通过算法产生初始种群[WTHX]X=［X1，X2，…，X[WTBX]t，…，[WTHX]X[WTBX]size］T，其中每一个解向量可以表示为[WTHX]X[WTBX]t=［X1t，X2t，…，Xlt］，解向量中的每个元素的选择由各工序的生产路径约束信息决定。算法开始时的迭代次数为0，在迭代中不断增加。

2.若当前迭代次数小于最大迭代次数，即i<imax，则表示当前可以继续循环迭代，通过适应度函数F（[WTHX]X[WTBX]t）计算解向量表示的总加工时间F（[WTHX]X[WTBX]t）（t∈［1，size］）；否则，输出当前种群中适应度函数值最大的最优解，其中适应度函数为

3实验（Experiment）

本文的数据来源为某大型工程机械装备制造企业的MES制造执行系统的图纸和工艺文件数据以及SAP企业资源管理系统中的生产计划数据；大型工程机械装备以盾构机为例，使用盾构机刀盘的部件及零件的最短加工路径作为算法的解。

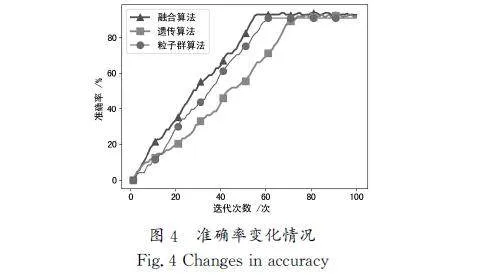
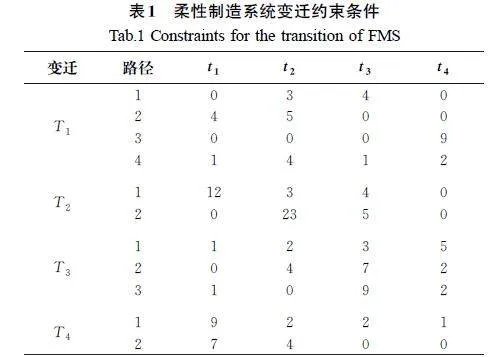
盾构机刀盘模块零部件包括中心刀、边刀、滚刀、铲斗、正刀、轮轴、主驱动，需要经过锻件车间、精加工车间、焊接车间和装配车间共计4个车间进行加工。使用柔性制造系统模型和各个车间的模型，根据Petri网的变迁使能表达式和表1所示的变迁约束条件，使用基于遗传算法和粒子群算法的融合算法对模型进行求解，得到最终的解序列，输出排产工序流程。同时，将融合算法在迭代过程中的目标函数值、结果准确率与遗传算法和粒子群算法进行比较。

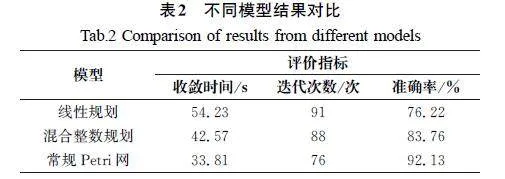
将本文提出的基于时延的Petri网模型和融合收敛算法与其他方法建立的模型性能进行对比，结果见表2。从表2中的数据可以看出，本文提出的模型在收敛时间、迭代次数、准确率方面均有所改善。

4结论（Conclusion）

本文提出一种基于时延Petri网建立大型工程机械装备柔性制造系统的建模方法，旨在模拟大型工程机械装备的柔性制造系统在实际生产过程中的各种调度情况，通过约束矩阵的辅助，能够很好地描述大型工程机械装备多部件、多零件、并行度高的特点。该模型充分发挥了Petri网逻辑模型用于描述和分析异步并发系统的优势，具有精确的定义、坚实的基础支撑，避免了模糊性、不确定性和矛盾性，使原本复杂的制造系统变得简单、直观。

在建立模型之后，本文提出了一种基于遗传算法和粒子群优化的融合算法对模型求解。这种算法具有遗传算法中强大的全局搜索能力，以及粒子群优化算法具有的通过随机扰动跳出局部最优解的能力。首先通过遗传算法在解集中获取较优解，其次通过粒子群优化对包含较优解的集合进行随机扰动，从而避免陷入局部最优解的情况。通过该算法的求解后，可以得到一个包含最优解的解集，其中的个体相较于传统的采用单一算法进行求解的结果，具有适应度更高、收敛速度更快、误差更小的优势，在并行度较高的柔性制造系统中可以最大化地提升资源利用率，优化企业在生产过程中的调度方式。

参考文献（References）

［1］张宁，林海华，孙亚平，等.鱼雷装备测试维修Petri网模型与指标论证分析［J］.兵工学报，2023，44（3）：886＼|894.

［2］闫哲，刘伟，杜玉越.基于逻辑博弈概率Petri网的地铁应急决策建模与分析［J］.系统仿真学报，2023，35（7）：1602＼|1618.

［3］贾云富，张凯.基于Petri网的机床座类柔性生产线调度模型［J］.机电工程，2022，39（10）：1470＼|1476.

［4］王慧英，周恺卿，周辉.基于约束优化的Petri网可达性FU模型［J］.计算机仿真，2022，39（6）：408＼|411，416.

［5］樊海刚，郭红梅，张莹，等.随机Petri网在地震应急协同能力定量评价与动态分析中的应用［J］.中国地震，2022，38（2）：248＼|259.

［6］徐海军，李彦斌，王进，等.基于模糊Petri网的有载分接开关故障诊断方法研究［J］.中国安全生产科学技术，2022，18（5）：222＼|228. ;

［7］YANGR，WUM，GUIXQ，etal.IntelligentconflictdetectionofIoTservicesusinghigh＼|levelPetrinets［J］.Complex&intelligentsystems，2024，10（3）：3789＼|3817.

［8］KABASHKINI，SANSYZBAYEVAZ.Methodologicalframeworkforsustainabletransportcorridormodelingusingpetrinets［J］.Sustainability，2024，16（2）：489.

［9］CUIYY，MALY，DINGQM，etal.AircraftturnaroundtimedynamicpredictionbasedonTimeTransitionPetriNet［J］.PLoSone，2024，19（7）：e0305237.