多吸引子忆阻混沌系统在图像加密中的应用

【摘 要】 为增强图像加密安全性，基于Lorenz混沌系统设计了一种新型的多吸引子忆阻混沌系统。通过最大李雅普诺夫指数图、分岔图和双参复杂度图进行理论分析和仿真，结果显示该系统具有共存吸引子现象，验证了系统具有超混沌特点及对初始值的高敏感性。此外，利用该系统在高复杂度区间生成的混沌序列对图像矩阵进行扩散、置乱、旋转及循环处理，实现图像的加密。通过直方图、信息熵及相邻像素相关性分析，证实了该算法具有较高的加密性能。

【关键词】 多吸引子忆阻混沌系统；共存吸引子；图像加密

Application of Multi-attractor Memristor Chaotic System in Image Encryption

Dai Wenpeng1， Chen Heng2*， Song Li1， He Na1， Yang Hongyu1

（1.Yantai Institute of Science and Technology， Yantai 265600， China;

2.Xijing University， Xi′an 710123， China）

【Abstract】 In order to enhance the security of image encryption， a new multi-attractor memristor chaotic system based on Lorenz chaotic system is designed. Through the theoretical analysis and simulation of the maximum Lyapunov exponent graph， the bifurcation graph and the two-parameter complexity graph， the author draws the conclusion that the system has the coexistence attractor phenomenon， and it is verified that the system is hyperchaotic and highly sensitive to the initial value. In addition， the chaotic sequence generated by the system in the high complexity region is used to diffuse， scramble， rotate and cycle the image matrix， so as to realize the image encryption. Through the analysis of histogram， information entropy and the correlation of adjacent pixels， the author confirms that the algorithm has high encryption performance.

【Key words】 muti-attractor memristor chaotic system; coexisting attractors; image encryption

〔中图分类号〕 TN601 〔文献标识码〕 A 〔文章编号〕 1674 - 3229（2024）03 - 0060 - 08

0 引言

多吸引子混沌系统结合了具有记忆性的忆阻器，增加了系统的随机性和不可预测性，从而使得系统的动态行为更为复杂［1-2］。由于混沌序列的复杂性，系统更难被攻击者预测，有效增强了抗攻击能力。同时，由于数字图像像素之间的强关联性，混沌系统应用于图像加密中，可以有效打破这种关联性，从而进一步提高密文的抗攻击性［3-6］。因此，对Lorenz混沌系统进行模拟和改进，以提高系统复杂度，并将改进后的系统与加密算法相结合，不仅增强了像素的随机性，也为提高加密算法的安全性提供了新的思路，显示出该系统在图像加密领域的重要应用价值。

首先，通过引入正弦函数、忆阻器到模拟Lorenz系统中，构建了多吸引子忆阻混沌系统。使用Matlab进行数值计算和仿真，验证了该系统能够根据初始条件及参数变化显示出复杂的动态行为。其次 ，利用该系统在高复杂度区间生成的混沌序列，执行图像加密过程中的各种操作，包括扩散、置乱、旋转和循环运算，此操作有助于破坏图像数据中像素之间原有的关联性，从而实现图像的有效加密［7-8］。最后，通过对加密图像信息熵、直方图及相关性分析，表明该系统的算法复杂性强，能够显著提高图像加密的安全性能。

1 多吸引子忆阻混沌系统

杜传红［9］替换Lorenz系统非线性项，使用绝对值函数和双极转换常数，模拟出Lorenz系统：

[x=a（y-x）y=（c-z） sign （x）z=|x|-bz] （1）

分段二次型有源磁控忆阻器模型为：

[q（φ）=-aφ+0.5φ2sgn（φ）]

忆导为：

[w（φ）=dq（φ）dφ=-a+b|φ|] （2）

对于系统（1），引入正弦信号及忆阻器模型（2），构建新的多吸引子忆阻混沌系统：

[x=a（y-x）+0.5sign（sin（0.05t））y=（c-z） sign （x）z=w|x|-bzw=-k1|z|+k2w] （3）

系统初值[x0=0.1]、[y0=0.1]、[z0=1]、[w0=3]，系统参数[a=1.2]、[b=1.8]、[c=2]、[k1=0.1]、[k2=0.2]、[m=5]、[n=0.2]时，系统（3）相图如图1所示，显示存在2个混沌吸引子。计算得到该系统的李雅普诺夫指数（LE）分别为[λ1=0.336]、[λ2=0.304]、[λ3=-1.005]、[λ4=-2.035]，有两个正的LE，说明系统（3）具有超混沌特性。

2 平衡点及共存吸引子分析

将系统（3）设为零，分析该系统在没有加入脉冲信号时的平衡点：

[a（y-x）=0（c-z）sign（x）=0w|x|-bz=0-k1|z|+k2w=0] （4）

得出平衡点为：

[E1=（0，0，0，0）]、[E2=（0.08，0.08，2，-0.2）]。

加入脉冲信号[signsin（0.05t）]时：

[a（y-x）+0.5signsin（0.05t）=0（c-z）sign（x）=0w|x|-bz=0-k1|z|+k2w=0] （5）

得出平衡点为：

[E3=（0，0±0.42，0，0）]、[E4=（0.08，0.08±0.42，2，-2）]。

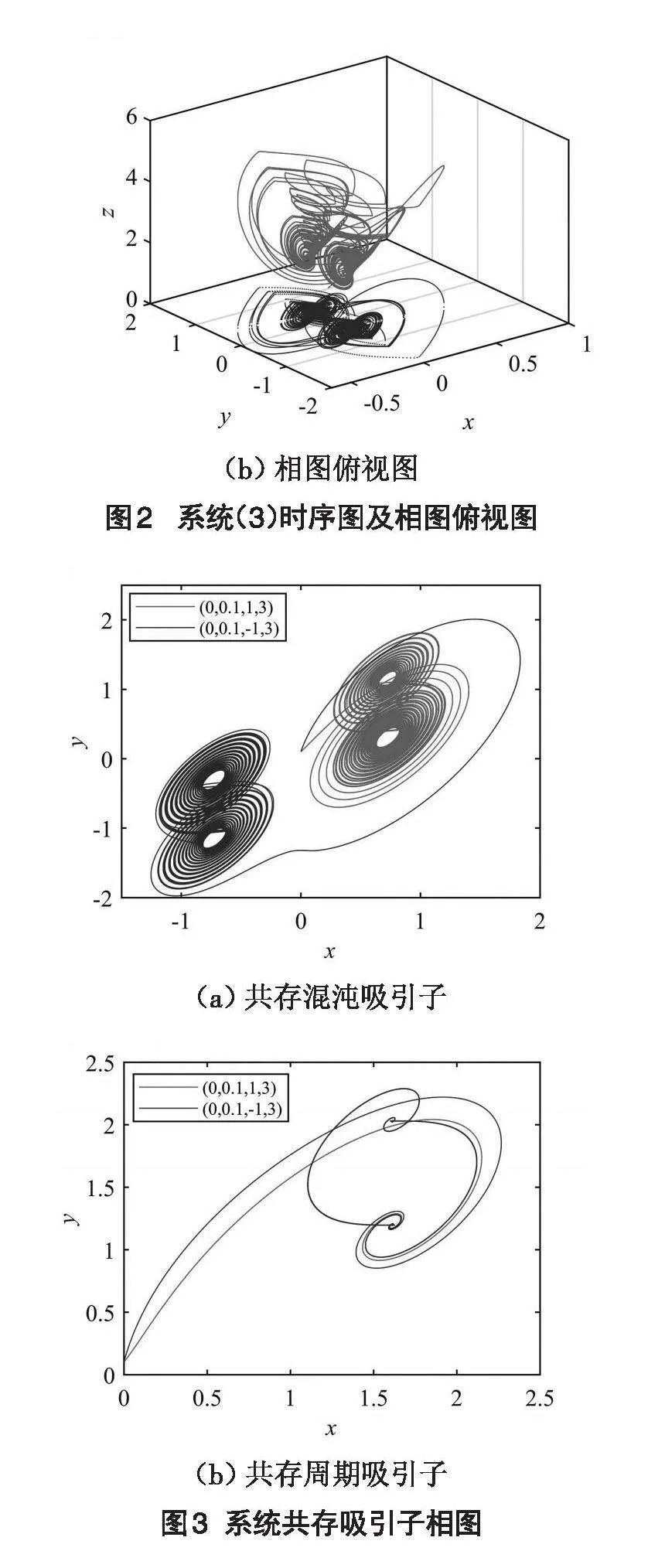
通过公式（4）、（5）结果对比，发现系统（3）平衡点在[y]方向上平移了±0.42个单位，说明该系统的动态性较强。从图2（a）系统在[y]轴上的时序图中可以看出，虚线代表的脉冲信号对系统产生了显著影响。在脉冲信号的控制下，[y]方向的波形沿着脉冲信号上下移动，振幅在±2之间，振荡中心在大约±0.42之间。表明脉冲信号使得系统的平衡点沿着[y]轴方向发生了±0.42个单位的平移。图2（b）的相图俯视图进一步验证了这一结果，相图清晰地展示了在脉冲信号作用下，系统在相空间中的轨迹发生了显著变化，引发了多吸引子混沌现象的出现，表明系统的动力学行为变得更加丰富。

当[a=1.2]、[b=1.8]、[c=2]、[k1=0.1]、[k2=1]、[m=5]、[n=0.2]、[x0=0]、[y0=0.1]、[z0=±1]、[w0=3]时，系统出现共存混沌吸引子，如图3（a）所示；取[b=4]，出现共存周期吸引子，如图3（b）所示，说明系统受初值影响敏感。

3 系统参数分析

首先，研究模拟Lorenz系统参数[a]、[b]、[c]在4个方向上的LE图，如图4所示。系统（3）变量分别设定为特定值时发现：仅参数[a]发生变化时，系统处于弱混沌状态，如图4（a）；仅参数[b]发生变化时，系统在[b∈[0，2）]上展现出混沌态，在[b∈[2，10]]上为周期态，如图4（b）；仅参数[c]变化时，系统则进入超混沌态，如图4（c）。鉴于高复杂度的混沌序列能够增强图像927c5c9b953d5c2a1c056599d7c88ccf加密的安全性。因此，所选定的参数值[a=1.2]、[b=0.2]、[c=2]符合该要求。

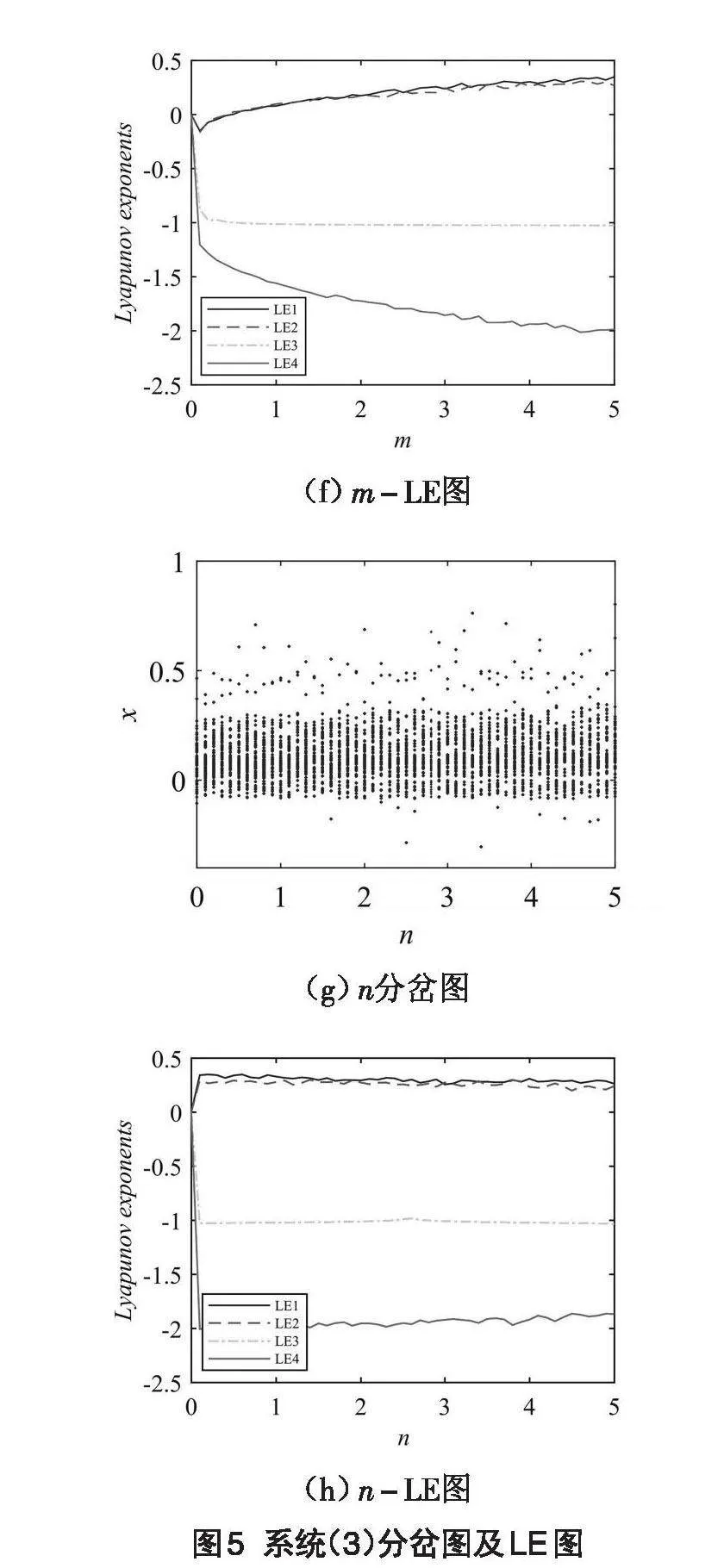
为更好地研究忆阻器相关参数对系统的影响，绘制了系统（3）在4个方向上的LE图、分岔图以及双参数复杂度图。当参数[k1]单一变化时，系统呈现超混沌状态，具体如图5（a）、5（b）所示；当参数[k2]单一变化时，系统同样为超混沌状态，如图5（c）、5（d）所示；当[m]单一变化时，系统在[m=0.2]附近为周期状态，而其余区间则为超混沌态，具体如图5（e）、5（f）所示；最后，当参数[n]单一变化时，系统再次呈现超混沌状态，具体如图5（g）、5（h）所示。说明忆阻器的引入，系统整体呈现为超混沌态，提高了系统的复杂度。因此，选择复杂性较强的参数[k1=0.1]、[k2=0.5]、[m=5]、[n=0.2]，作为后续加密应用的参数。

当[a=1.2]、[b=1.8]、[c=2]、[k1=0.1]、[k2=0.2]时，做系统（3）的[m-n]双参数复杂度状态图。其中，暗红色部分代表复杂度最高，橙色部分代表复杂度较高，黄色部分代表复杂度一般，绿蓝色部分代表复杂度较低，如图6（a）所示。当[m=5]时，[n∈[0，5]]区间复杂度相似且为强复杂区，与图5（h）关于的[n]单参数LE变化一致。当[n=0.2]，[m∈[0，5]]区间复杂度呈上升趋势，且在[m=5]处复杂度较强，与图5（f）关于[m]的单参数LE变化一致。

当[a=1.2]、[b=1.8]、[c=2]、[m=5]、[n=0.2]时，系统（3）的[k1-k2]双参数复杂度图见如图6（b）。当[k1=0.1]时，[k2∈[0，5]]区间复杂度相似且为强复杂区，与图5（d）关于[k2]的单参数LE变化一致。当[k2=0.2]，[k1∈[0，5]]区间复杂度呈微弱下降趋势，且在[k1=5]处复杂度相对较小，与图5（b）关于[m]的单参数LE变化一致。

从图6得出[k1=0.1]、[k2=0.2]、[m=5]、[n=0.2]在强复杂度区间内，为后续加密参数的设定提供依据。

综上所述，系统参数采用[a=1.2]、[b=0.2]、[c=2]、[k1=0.1]、[k2=0.5]、[m=5]、[n=0.2]，系统初值采用[x0=0.1]、[y0=0.1]、[z0=1]、[w0=3]，应用于后续图像加密中，混沌序列复杂性较高，使加密后的图像破解难度增加，更具有安全性。

4 图像加密仿真及安全验证

4.1 加密方案

系统加密方案如图7所示，具体流程为：

Step1：读取原始图像信息，获取图像矩阵像素值；设定初始值（密钥[x0]、[y0]、[z0]、[w0]）及系统参数，利用多吸引子混沌系统产生X、Y、Z、W、U、V混沌矩阵及混沌元素a、b。

Step2：将X混沌矩阵及混沌元素a与图像矩阵P进行异或运算，将前向扩散后的矩阵旋转180°并通过Z、W、U、V混沌矩阵进行图像矩阵位置的置乱，将得到的矩阵旋转180°，形成新的矩阵。

Step3：将Y混沌矩阵及混沌元素b与Step2得到的图像矩阵进行异或运算，得到的矩阵后向扩散并旋转180°输出加密矩阵。根据设定值n进行以上工序的进步加密，输出加密图片。

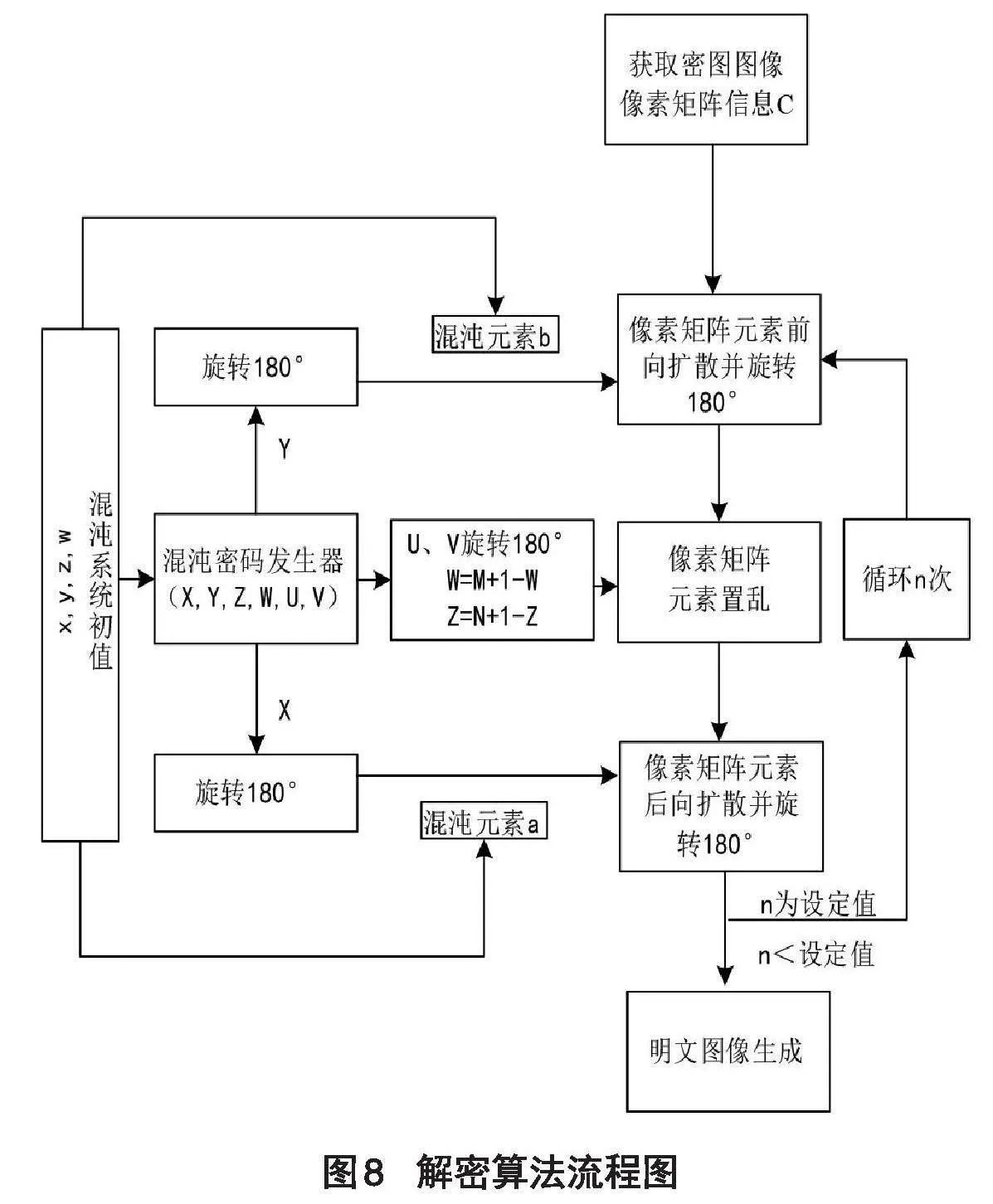
4.2 解密方案

解密过程是加密过程的逆过程，首先授权用户使用相同的混沌序列对加密后的矩阵像素值进行逆向替换，然后再进行逆向置换，最终恢复出原始图像，具体流程如图8所示。

Step1：读取密图图像信息，获取图像矩阵元素值；配置初始值（密钥[x0]、[y0]、[z0]、[w0]），利用多吸引子混沌系统产生X、Y、Z、W、U、V混沌矩阵及混沌元素a、b。

Step2：将旋转180°后的Y混沌矩阵同混沌元素b与密图矩阵C进行前向扩散，将扩散后的矩阵旋转180°。输出的矩阵通过变化后的Z、W、U、V混沌矩阵进行元素位置的置乱，将置乱后的矩阵旋转180°，根据设定值n进行工序的进一步循环，输出原始图片。

4.3 算法验证及图像直方图分析

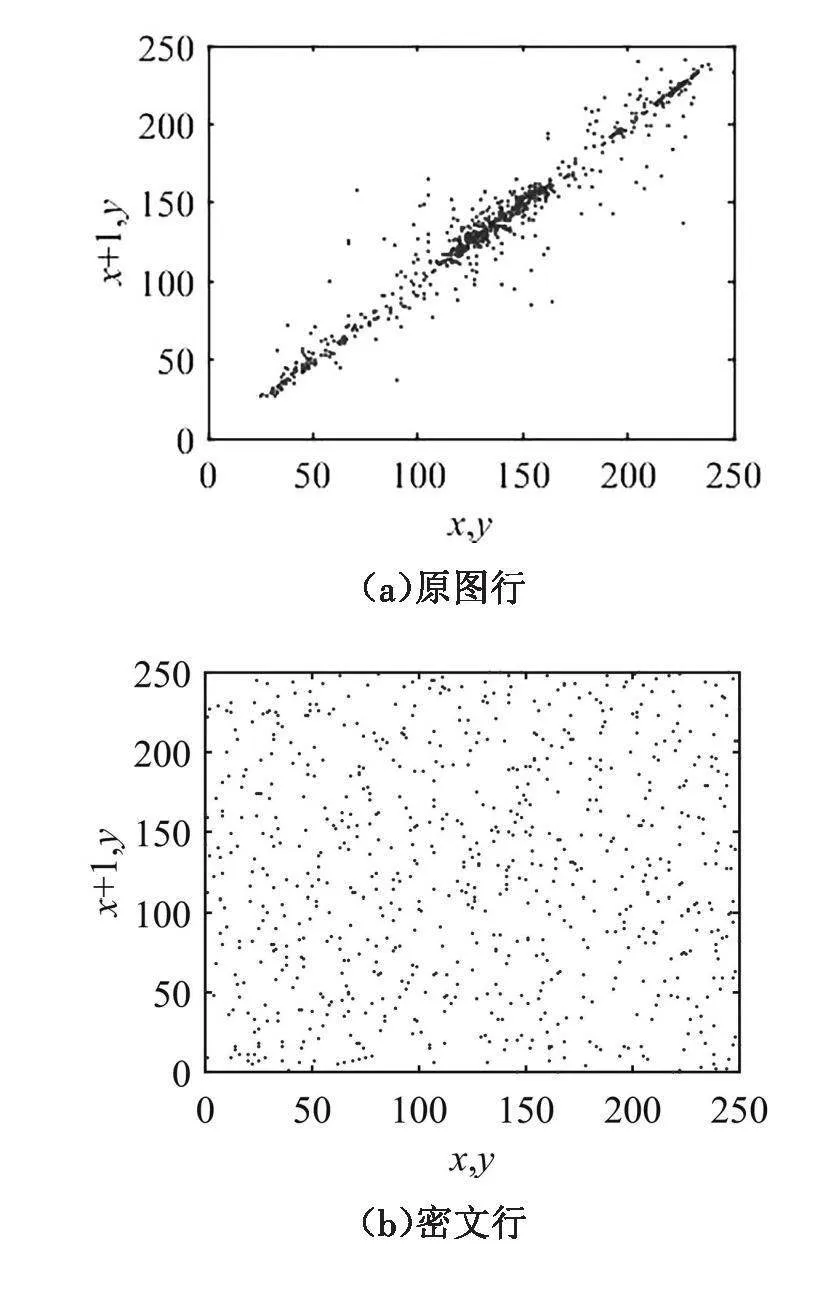
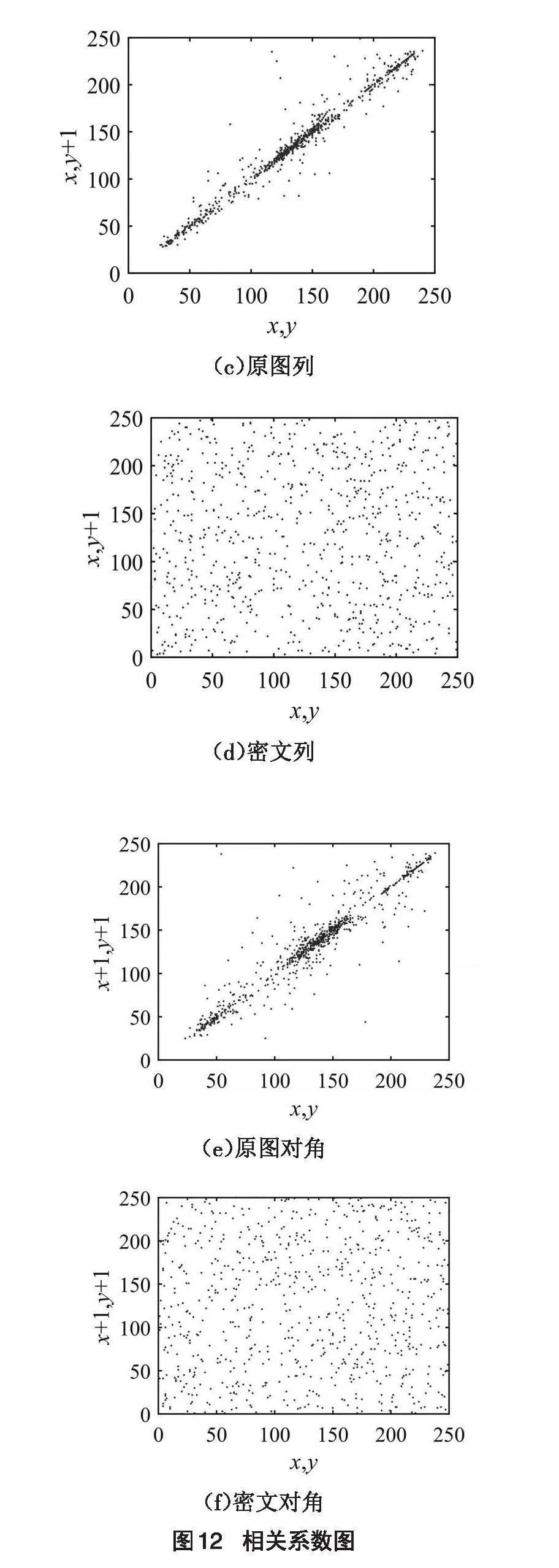
采用基于多吸引子的图像加密算法对雪景原图加密，加密后的雪景密图如图9（b）所示，经该算法得到的雪景解密图如图9（c）所示。图9（a）雪景原图与雪景解密图一致，实现了图像信息加密及解密。为进一步验证该算法的有效性，从图像内在的像素值分布情况进行分析，根据图10（a）原图像素值分布情况，得出原图像素值分布随机性弱，像素值具有一定的关联性，数学统计特性强。根据图10（b）密图像素值分布情况，得出密图像素值分布具体高度随机性，像素值关联性很弱，数学统计特性不明显。根据图10（c）解密图像素值分布情况，得出解密图像素值分布情况与10（a）原图像素值分布情况基本一致。充分验证了该算法的有效性。

图像直方图是对像素数据统计的一种方法，用以表示图像灰度值的像素数分布情况［9-10］。横坐标表示灰度值，纵坐标表示该灰度值出现的频次。原图像的灰度频次分布不均匀且统计特性明显，如图11（a）所示，密图的灰度频次分布更均匀，且直方图统计特性不明显，如图11（b）所示。说明该算法具有抗统计攻击特性。

4.4 信息熵及相关性分析

信息熵值反映像素值混乱程度，信息熵越大时像素值越乱，反之越小［11］。经计算得出原图信息熵为7.4531，密文信息熵为7.9999，接近理论值8，加密效果较好。为研究像素相邻元素相关性，对原始图片及加密图片进行像素值相关性分析，相关性计算公式为：

[ρx，y=cov（x，y）D（x）+D（y）] （6）

其中：

[D（x）=1Ni=1Nxi-E（x）2]，[D（y）=1Ni=1Nyi-E（y）2]

[cov（x，y）=E（x-E（x））（y-E（y））]。

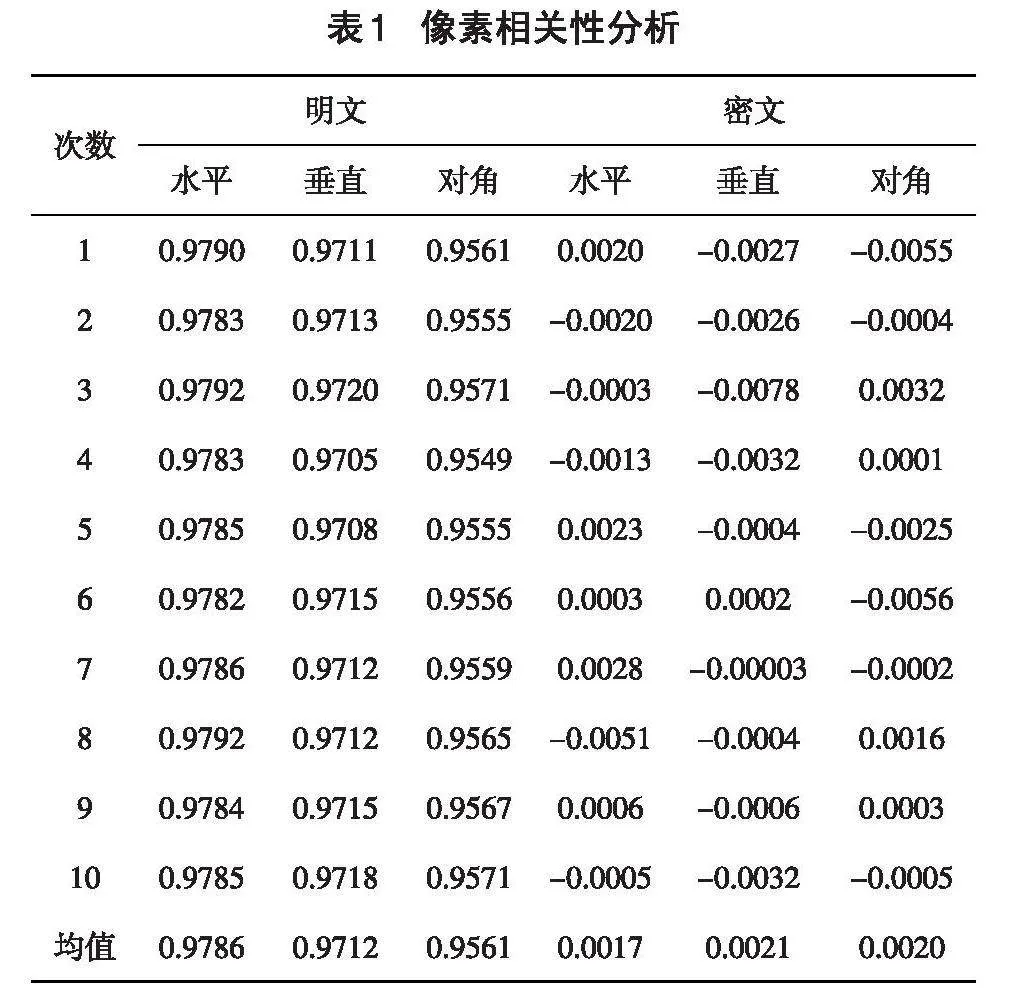
随机抓取10次，进行绝对平均值处理，每次统计10000个像素点的相关系数值，如表1所示。原图行、列、对角方向的相关系数为0.9786、0.9713、0.9561，密图相关系数为0.0017、0.0021、0.0020。结果表明，经该算法加密后，图片矩阵像素值相关性较低，加密算法有效。

图像化直观展示相关性，由图12（a），12（c），12（e）可知，原图像素间相关性显著，由图12（b），12（d），12（f）可知，密图像素间相关性弱。说明该算法能够有效降低相关性，提高图像加密性能。

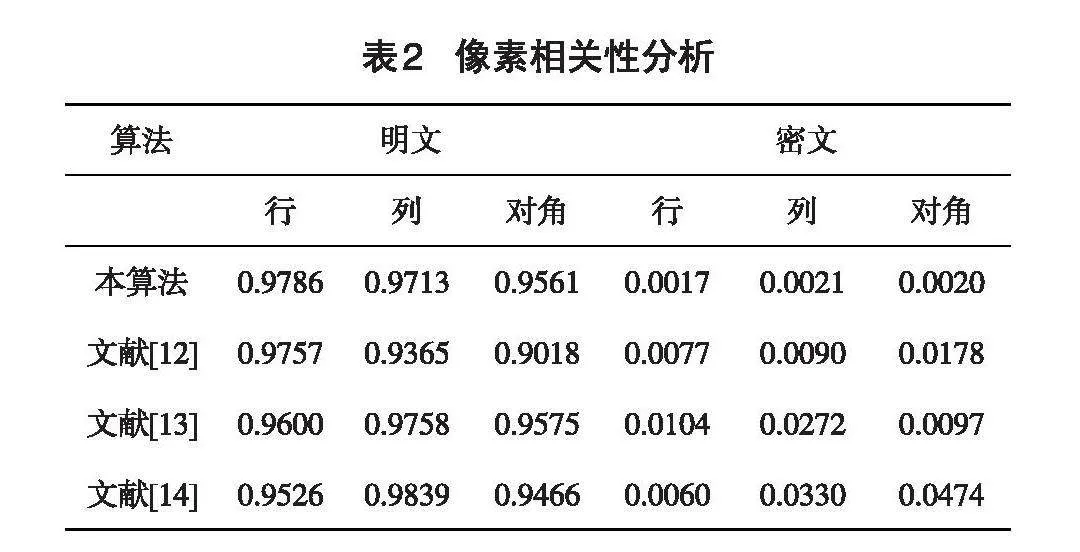
为充分验证该算法有效性，表2列出了基于多吸引子混沌系统加密算法与其他算法的对比数据，其相关性系数值说明本算法可以有效降低像素离散程度，安全性较好。

5 结论

本文基于Lorenz混沌系统设计了一种新型的多吸引子忆阻混沌系统应用到图像加密中，以增强图像加密的安全性能。首先，通过分岔图、LE图、相图及复杂度图分析了该系统动力学特性，验证了系统具有超混沌特点及动态复杂性。基于此发现，提出高复杂度区间的混沌序列对图像矩阵进行扩散、置乱和旋转处理相结合的方案，通过直方图、信息熵和相邻像素相关性的分析等方法证明本加密方案可以很好地隐藏明文图像的信息，加密效果较好。

［参考文献］

［1］ 曹可，赖强，赖 聪.含多吸引子的忆阻混沌系统的分析与实现［J］.深圳大学学报，2022，39（4）：480-488.

［2］ 秦铭宏，赖 强，吴永红.具有无穷共存吸引子的简单忆阻混沌系统的分析与实现［J］.物理学报，2022，71（16）：146-156.

［3］ 颜闽秀，张 萍.保守系统的类混沌吸引子共存分析及图像加密［J］.兰州理工大学学报，2023，49（5）：102-111.

［4］ 高若云，白牡丹，黄佳鑫，等.基于多混沌系统的多图像加密算法［J］.计算机系统应用，2024，33（3）：170-177.

［5］ 刘思洋，王越，李寒.基于超混沌系统及有限域的图像加密算法［J］.河北师范大学学报，2024，48（2）：129-140.

［6］ 代文鹏，陈 恒，焦方桐，等.一类新型纠缠混沌系统的电路设计及在图像加密中的应用［J］.廊坊师范学院学报（自然科学版），2023，23（1）：22-28.

［7］ 蔡正保.一种基于混沌加密和小波变换的数字水印技术研究［J］.廊坊师范学院学报（自然科学版），2016，16（2）：17-21.

［8］ 胡超飞，尹毅峰，刘琨鹏.基于序列密码的图像加密算法［J］.湖北民族大学学报，2021，39（1）：67-71.

［9］ 杜传红，刘立才，张谢馥，等.模拟Lorenz混沌系统电路设计［J］.科技创新与应用，2017（10）：24.

［10］ 韦斌，隋宇，邓小玉，等.基于频域压缩和二维离散混沌的图像加密方案［J］.计算技术与自动化，2023，42（4）：110-116.

［11］ 郭现峰，李浩华，魏金玉.基于Fibonacci变换和改进Logistic-Tent混沌映射的图像加密方案［J］.吉林大学学报，2023，53（7）：2115-2120.

［12］ 王伟杰，姜美美，王淑梅，等.基于量子长短期记忆网络的量子图像混沌加密方案［J］.物理学报，2023，72（12）：21-32.

［13］ 张勋才，刘奕杉，崔光照.基于 DNA 编码和超混沌系统的图像加密算法［J］.计算机应用研究，2019，36（4）：1139-1143.

［14］ LI W， CHANG X Y， YAN A M， et al. Asymmetric Multi- ple Image Elliptic Curve Cryptography［J］.Optics and Lasers in Engineering， 2021， 136： 1-10.

［15］ FIRDOUS A，UR REHMAN A，SAAD MISSEN M M. A Highly Efficient Color Image Encryption Based on Linear Transformation Using Chaos Theory and SHA-2 ［J］.Multimedia Tools and Applications， 2019， 78（17）： 24809-24835.

责任编辑 吕荣荣

［收稿日期］ 2024-05-11

［基金项目］ 陕西省重点研发计划（2018GY-091）；西安市科技创新引导项目（201805043YD21CG27-2）

［作者简介］ 代文鹏（1991- ），男，硕士，烟台科技学院海洋工程学院教师，研究方向：开关电源与混沌控制。

［通讯作者］ 陈恒（1965- ），男，博士，西京学院副教授，研究方向：混沌控制与机器人技术。