设计游戏活动助力学生推理能力提升的实践

【摘 要】在数学游戏课中，教师要将数学问题融入游戏之中，能让学生在主动参与游戏活动的同时，潜移默化地学习数学知识和数学思想方法。以二年级数学游戏“兔妈妈的格子菜地”为例，教师在对游戏原理进行解读，对游戏内容进行分析的基础上，通过创设问题情境，设置游戏进阶升级关卡，引导学生主动参与游戏，经历思考过程，积累活动经验，发展数学思维。

【关键词】数学游戏；数方；推理意识；空间想象力

在数学游戏课中，教师要将数学问题融入游戏之中，能让学生在主动参与游戏活动的同时，潜移默化地学习数学知识和数学思想方法。如何选择合适的学习素材，能够将游戏的乐趣与数学的学习深度融合，助力学生推理能力的提升？如何将学生对游戏的热情转化为数学学习的动力？笔者以二年级数学游戏“兔妈妈的格子菜地”为例进行探讨。

一、游戏解读与教学分析

（一）游戏原理解读

数学游戏“兔妈妈的格子菜地”源自数方游戏。数方是一种逻辑解谜游戏，将数字与图形紧密结合，游戏过程富有挑战性，主要锻炼玩家的逻辑思维能力、计算能力和空间想象能力，是一款体现数形结合思想的逻辑游戏。游戏的道具是长方形（或正方形）格子图，图中散布着若干数字（如图1）。游戏规则要求玩家将所有格子划分为若干个长方形或正方形区域，每个数字代表其所在区域内小方格数量，且同一个格子不能被重复划分。玩家需通过逻辑推理，根据数字确定每个区域的形状及位置，最终完成整个长方形（或正方形）格子的划分。

例如，在图1所示的4×4的格子上，玩家可以将最大的数字4作为突破口，确MA5ji/gvD5KdWELcdK6RrItwYxLRy2b+Nf2mKheAWzE=定4所在的区域只能是正方形而不能是长方形，接着根据其他数字依次推理划分，直至整个大正方形被完整分割。

（二）游戏内容分析

1.创设富有童趣的游戏情境

二年级学生的思维特点以形象直观为主。因此，笔者为数方游戏设计了“兔妈妈分菜地”的游戏情境，以轻松有趣的动物故事激发学生解决问题和挑战问题的兴趣。

2.结合已有知识经验的应用

学生在一年级已经初步了解了长方形和正方形的特征，并在二年级学习了表内乘法。因此，在游戏教学中，教师引导学生将数字与形状相结合，在动手操作中识别不同的几何形状，感知不同形状在格子中的排列和组合，理解长方形、正方形与格子数之间的对应关系。例如：数字4可能对应4×1的长方形或2×2的正方形；数字6可能对应6×1或3×2的长方形等。通过观察和操作，将抽象的数字与具体的几何形状联系起来，有助于培养学生的空间观念。

3.设置具有挑战的游戏层阶

作为一款游戏，层阶性的挑战闯关是不可或缺的。这不仅能够激发学生的好奇心和求知欲，而且能在有趣好玩的过程中培养学生的推理意识。因此，在明确游戏规则后，教师引导学生尝试操作，并设计了一个活动和三个挑战任务（如图2）。

在游戏活动中，学生通过观察信息，分析信息，应用信息，边操作边概括总结求胜策略。将最大数或边角上的数作为突破口，观察并找到形状唯一的图形；面对多种可能性时，先假设再排除，运用“假设—尝试—调整”的策略，直到挑战成功，从而培养逻辑推理能力。

基于上述理解，确立如下教学目标：

（1）加深学生对长方形和正方形特征的认识，通过探究菜地分割的数学问题，明确格子数与形状的联系，从而促进学生空间观念的发展。

（2）在尝试、推理、概括等活动中，引导学生深入理解并准确运用游戏规则，形成有序且全面的思考方式，提高他们排除错误假设和进行逻辑推理的能力。

（3）通过师生互动和交流沟通，促进学生在数学语言表达和社会交往方面的发展，同时让学生体验数学游戏的乐趣。

二、游戏实施过程

（一）在操作辨析中掌握游戏规则

游戏规则是构成游戏的精髓，学生在参与游戏之前要先理解并熟练掌握这些规则，这样才能在游戏中准确判断自己和其他玩家是否遵守规则，并且有效地迎接游戏挑战。对于二年级学生而言，他们主要依赖具体形象思维，因此在理解游戏规则中复杂的文字描述时可能会遇到障碍，一次性理解所有规则对他们来说也颇具挑战。鉴于此，教师在游戏规则理解阶段采用了分段法和辨析法两种策略。通过两个阶段的具体操作和演示，逐步分解难点；接着通过正例和反例的辨析，迅速将游戏规则聚焦于数量和形状这两个关键维度，帮助学生掌握游戏的核心要素。

【教学环节1】创设情境，理解规则

1.初步了解游戏规则

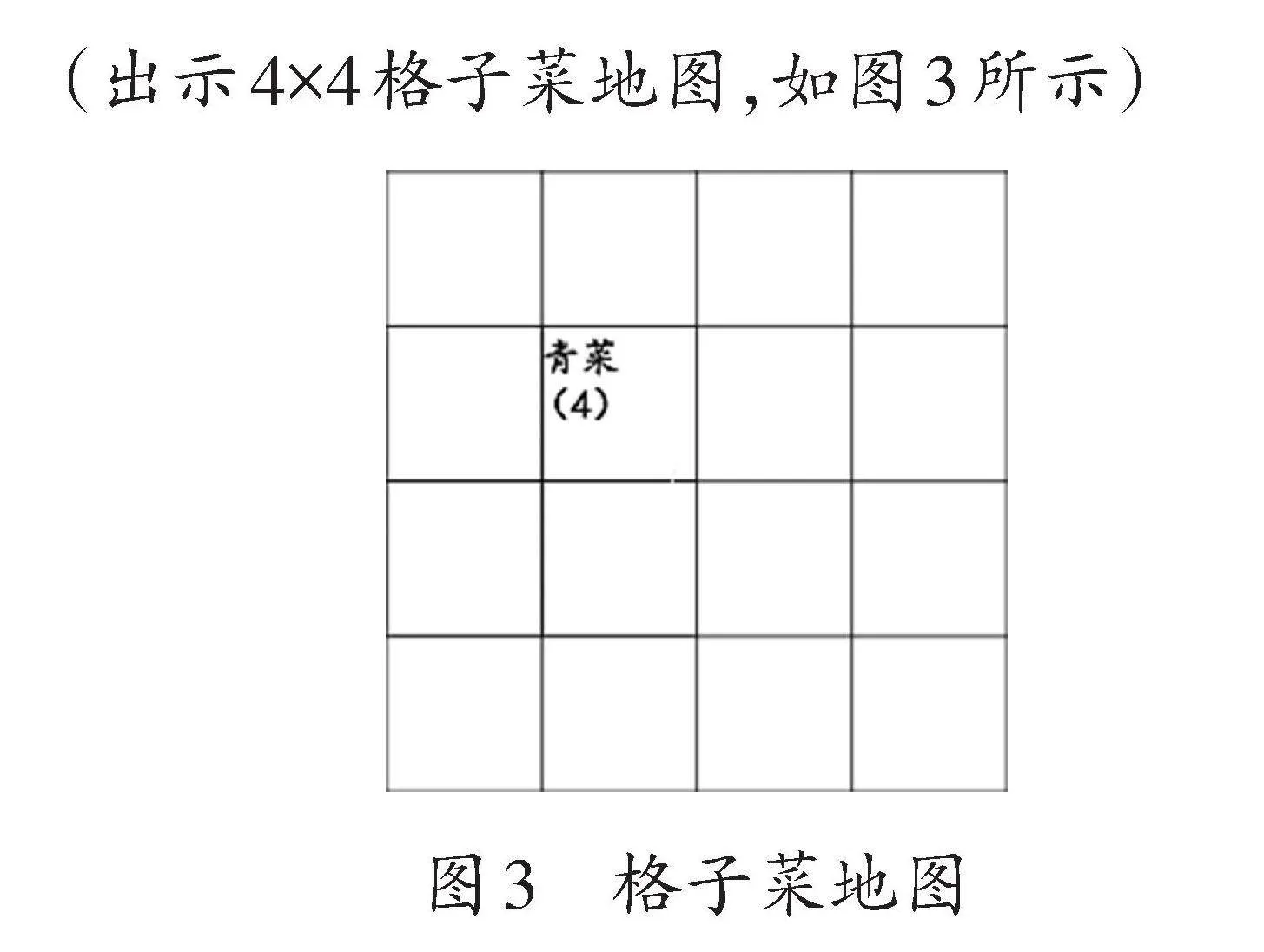
（出示4×4格子菜地图，如图3所示）

师：兔妈妈将格子菜地分割成长方形或者正方形，准备种植一些蔬菜。其中一块地种植的是青菜，你知道青菜一共种植了几格吗？

生：菜地上写着“青菜（4）”，应该要种植4格。

师：学习数学就要有这样敏锐的眼光。再看看这4格青菜地还有什么特别的要求？

生：形状必须是长方形或正方形。

师（小结）：在观察格子菜地时，不仅要关注种植的格子数量，还要考虑菜地的形状。

2.逐步明晰游戏规则

师：4格青菜可以怎么种呢？请画一画。

生：我的青菜地是正方形，正好是占4个格子（如图4-①）。

生：我的青菜地也是正方形，不过位置有所不同（如图4-②）。

生：我也发现了不同的青菜种植位置，从左上角开始画，共画出了四种情况。

师：除了正方形之外，青菜还可以种在什么形状的菜地上呢？

生：还可以是长方形，一行4格或者一列4格（如图4-③④）。

师：真厉害。当青菜地占4格时，你们找出了所有可能的正方形和长方形种植位置。

师：小兔子还打算在菜地上种植土豆。土豆地要占3格，应该怎么种植呢？

生：可能是3格一行或者3格一列（如图5-①②③）。

师：可以是这种“L”的形状吗（如图5-④）。

生：L的形状既不是长方形也不是正方形，3格的菜地不可能是正方形，只能是长方形，要么在同一行，要么在同一列，否则就不符合游戏规则。

师（小结）：在关注菜地形状与数量的同时，还需要有序地进行思考，这样才能使菜地形状的排列具有更多的可能性。

在本教学环节中，教师通过提供一个格子数来寻找长方形、正方形的数学活动，让学生在理解规则的过程中进一步明确图形特征。教师通过格子数让学生想象构建不同的图形，并引导学生有序列举，为游戏挑战提供了更多可能性。

（二）在尝试调整中感悟游戏策略

在理解游戏规则之后，教师设计了图2中的挑战任务一，让学生在整块菜地上根据格子数大小和位置进行分割，引导他们思考最优解法，如寻找突破口、使用符号记录等方法。教师应重视学生思考的逻辑表达和数学活动经验的积累，引导学生逐步感悟并归纳游戏策略。

【教学环节2】初次尝试，感悟策略

（教师出示图2中的挑战任务一：4×3的格子菜地）

1.独立尝试，不断调整

师：小朋友们已经知道了格子菜地的秘密，现在让我们来挑战第一关。请按照格子菜地的数字把这块地种满，要求每位小朋友用对应的四种颜色的水彩笔画一画。学习单上提供了很多幅格子菜地图，如果涂错了，可以尝试涂第二幅图、第三幅图……

2.整体反馈，感悟方法

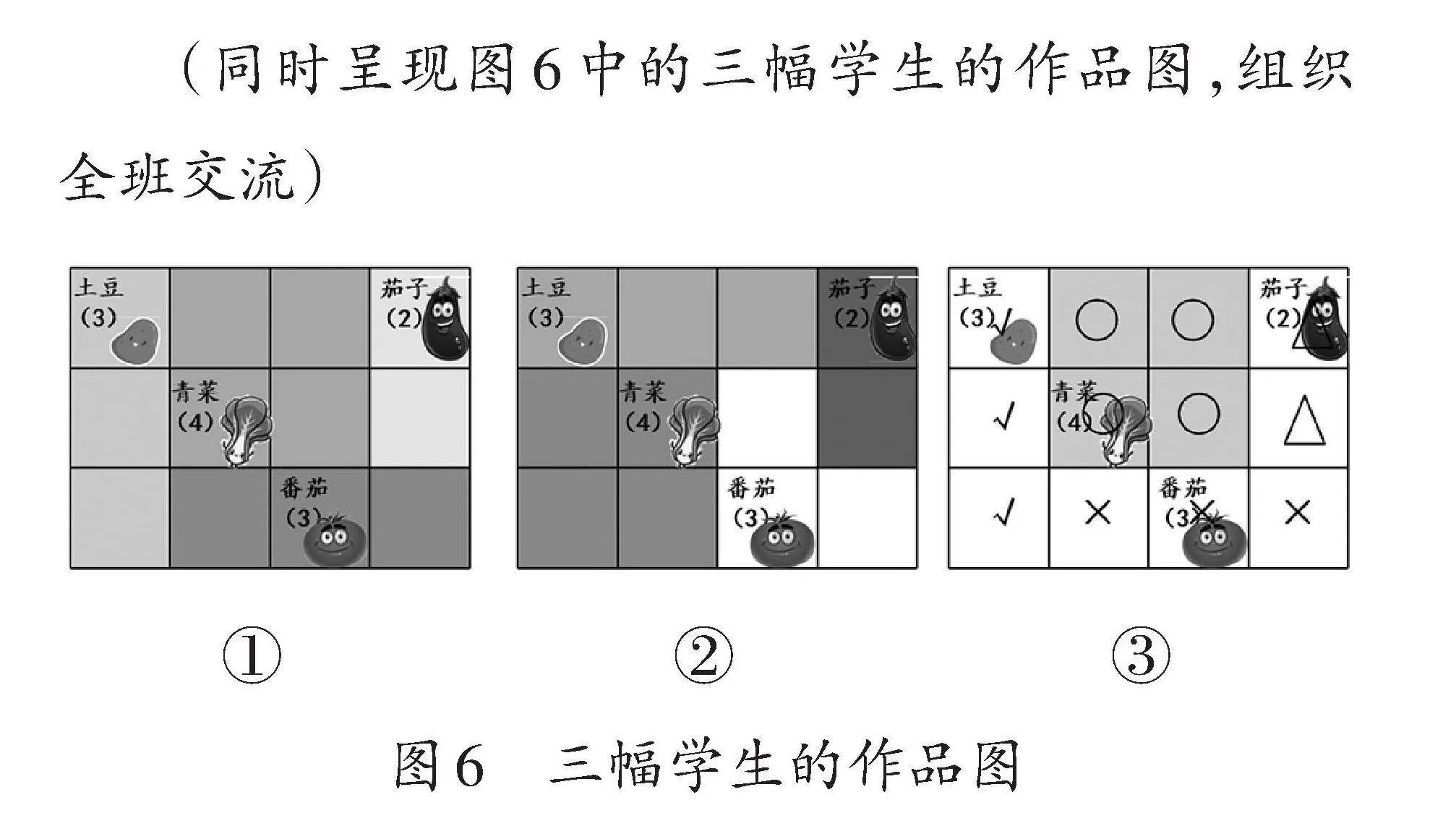
（同时呈现图6中的三幅学生的作品图，组织全班交流）

师：对于这三个同学画出的结果，你们有什么想说的？

（反馈一：学生作品图6-①）

师：他挑战成功了吗？我们怎么来验证呢？

生：成功了！土豆3格，青菜4格，茄子2格，番茄3格，四种蔬菜地的形状都是长方形或正方形。而且格子菜地里种满了蔬菜。

（反馈二：学生作品图6-②）

师：对于作品图6-②，你们有什么想说的？

生：先涂土豆、青菜、茄子，剩下的3格不是一个长方形，这种方法不对，这次挑战失败了。需要重新画。

生：我第一次也失败了，第二次涂图时，我把土豆地的位置换了一下，就成功了。

师：尝试时发现错误，就要重新调整再挑战。我们学习数学就需要这种勇于试错的精神。

（反馈三：学生作品图6-③）

师：这个小朋友画了一些符号，你们能看明白吗？

生：他用“√”“○”“△”“×”表示各种蔬菜地，这样如果出错，可以重新调整，找到正确的菜地。

师：这个小朋友真聪明。一边思考一边调整，这样的学习方法值得全班同学学习。

师（小结）：有的小朋友第一次尝试就成功了，有的小朋友用“尝试—调整”的方法，经过几次尝试也能种好。失败了不气馁，值得表扬！

这个教学环节从最简单的4×3格子图开始，是游戏的尝试阶段，难度较低，学生能快速获胜并体验成功的喜悦。教师鼓励学生在学习单上记录每次尝试的结果，在反馈交流中关注学生尝试过程中的成功和失败经验。通过互动交流，帮助学生回顾哪些做法容易成功，为什么有时几次尝试都会失败，有没有更好的方法……学生通过不断辨析，逐步归纳游戏取胜的策略。

（三）在进阶活动中发展推理意识

教师可将策略运用与闯关活动相结合，通过设置多层阶的进阶任务，引导学生从无目的的尝试转变为有策略、有目标的挑战，让学生在完成这些任务的过程中，发展推理意识。

【教学环节3】方法优化，拓展提升

1.挑战4×4的格子菜地

（出示图2中的挑战任务二：4×4的格子菜地）

师：如何才能又对又快地完成这块格子菜地的涂色任务呢？

生：先涂4格的青菜地。它不能涂成正方形，也不能涂成竖着的长方形，否则会出现重叠。那只能涂成横着的长方形，这是唯一的形状。

师：真厉害。通过观察，我们找到了青菜地这个突破口，这样就缩小了选择范围。

生：接下来，我们可以确定茄子地的位置，它不能横着涂，只能竖着向下分割。

生：我们也可以确定土豆地的位置，横着竖着分割都不行，只能在右下角划分出正方形。

师：没错，在游戏过程中，我们需要先明确哪些可以确定的因素，再不断尝试、不断调整，找到突破口，解决问题。

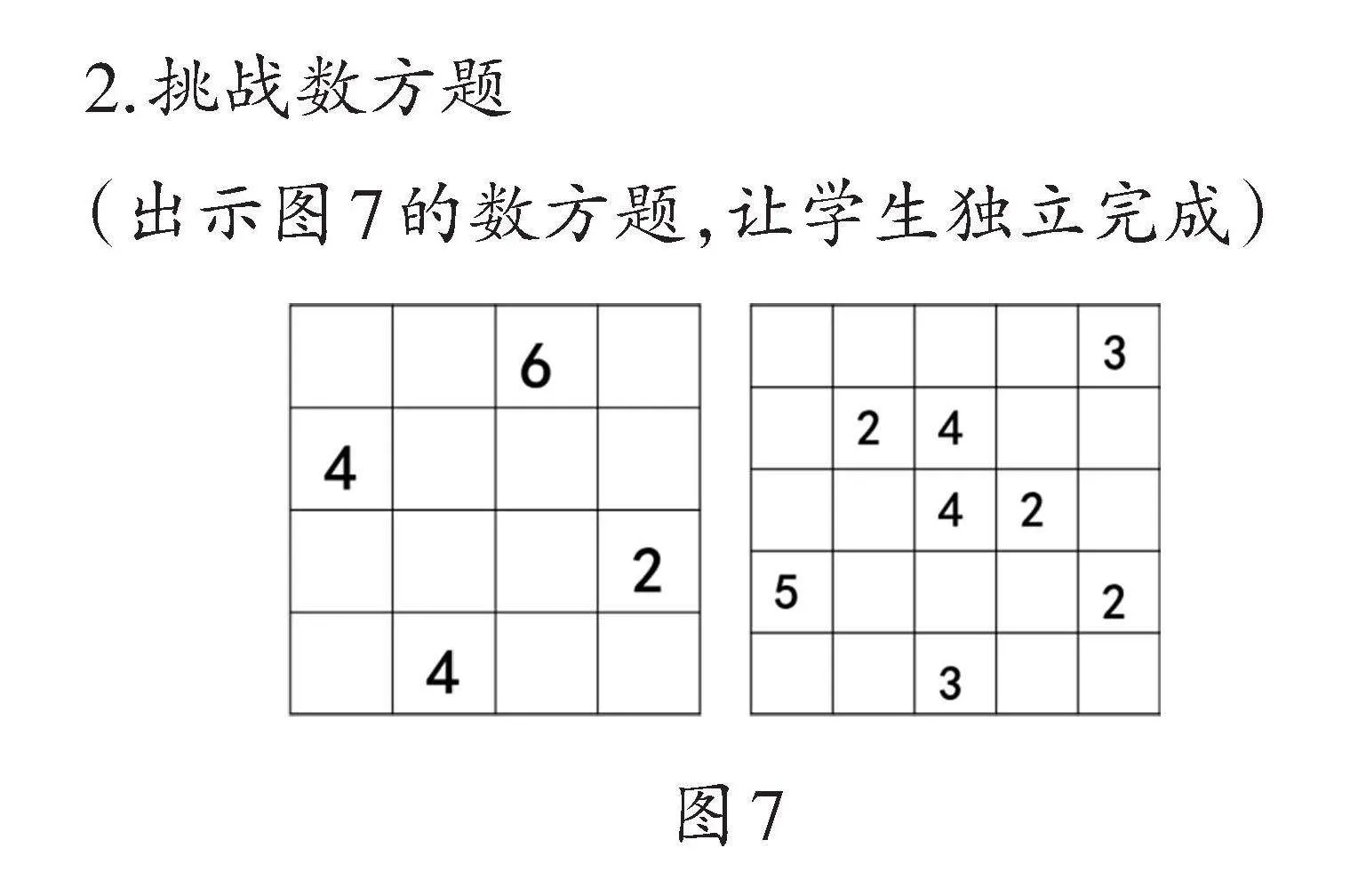
2.挑战数方题

（出示图7的数方题，让学生独立完成）

师：看看第三关的挑战，与前两关有什么不同之处？

生：菜地里的格子数量增加了许多，而且只给出了数字，其中还包括较大的数字5和6。

师：兔子妈妈的菜园不限制种植蔬菜种类，只告诉我们数字保持不变，形状还是长方形或正方形。请使用不同的颜色来表示数字所代表的格子数量。

师（小结）：我们需要不断地思考，不断地尝试，还要运用一定的策略。

这个教学环节属于熟练掌握规则并深入游戏的阶段。在这个阶段中，学生从具体情境过渡到抽象的数方概念，从无策略的尝试转变为有策略的推理。特别是当格子数量增加到6时，难度大大提升，不仅考验了学生的推理能力，还考量了他们的空间想象力。

总之，游戏因其娱乐性和大众化的特性，与数学的抽象性和逻辑性形成鲜明对比。数学游戏恰好能够将两者巧妙地结合起来，既保留了游戏的趣味性，又融入了数学的学科性。在数学游戏课中，教师应将游戏元素与数学相结合，通过创设问题情境，设置游戏进阶升级关卡，引导学生主动参与游戏，经历思考过程，积累活动经验，发展数学思维。

参考文献：

［1］张优幼.数学有意思［M］.杭州：浙江教育出版社，2019.

［2］张优幼.基于深度思维的数学游戏规则创编［J］.教学与管理，2019（11）：53-55.

［3］王晓蕾，尚建丽.感悟数学思想 发展核心素养：“数学游戏：汉诺塔”教学实录与评析［J］.小学数学教育，2022（23）：51-53.

（浙江省台州市椒江区中山小学杨司校区）