基于差分Mel倒谱法的音乐旋律特征提取算法

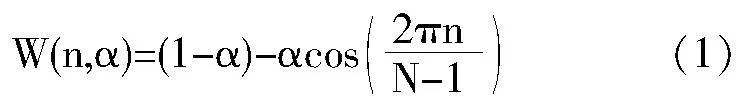

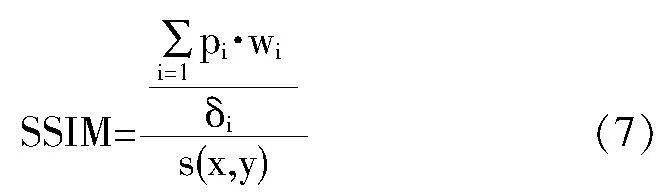
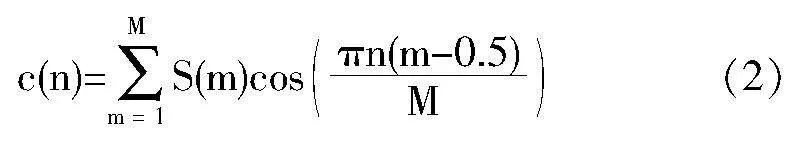
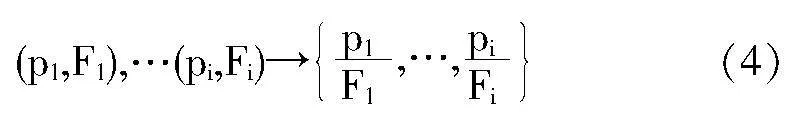
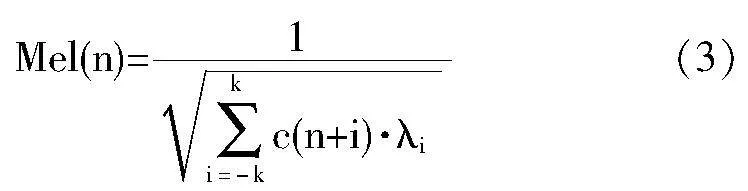

摘 要:由于忽略了基频序列的动态特性,导致音乐旋律特征提取效果不佳。对此,提出基于差分Mel倒谱法的音乐旋律特征提取算法。通过对帧长以及帧移进行设定,实现音频信号分帧处理,并结合汉明窗函数对其进行加窗处理。引入Mel倒谱系数,对音乐旋律的动态特性进行表征,实现基频提取。将音频序列转换为一维的音高序列,并针对序列进行分帧操作,从而得到音高向量信息。结合音高区间的分布情况统计结果,并在其中加入一定的区分性信息指标,得到音乐旋律的多维特征。实验结果表明,该算法应用后,旋律结构相似度指数较高,具备较为理想的提取效果。
关键词:梅尔倒谱系数;音乐旋律;特征提取;音高曲线
中图分类号:TP391 文献标识码:A 文章编号:1673-260X(2024)09-0070-05
在音乐信息检索(Music Information Retrieval, MIR)领域,旋律特征提取是至关重要的一环,它关乎音乐作品的识别、分类、检索等应用。
何丽等[1]通过多特征融合技术,将音频信号的时域、频域和倒谱域特征进行融合,以全面捕捉音乐的旋律信息,利用压缩激励模型对融合后的特征进行进一步处理,以增强主旋律特征的表示能力。但该方法在处理复杂多变的音乐风格时可能面临挑战,因为多特征融合可能会导致特征之间的冗余和冲突,从而影响主旋律提取的准确性。杨汶雯等[2]利用卷积神经网络(CNN)对音频信号进行特征提取,并通过全连接层进行分类。但该方法的不足之处在于其对训练数据的需求较大,且容易受到训练数据分布不均的影响。Zhang J W[3]利用循环神经网络(RNN)对音频信号进行序列建模,并通过多层感知器(MLP)进行分类。但该方法对于长时依赖关系的处理能力有限,可能导致在处理复杂音乐结构时表现不佳。Zhang K D[4]利用音频处理技术提取音乐的多种特征,并结合线性分析法对其进行融合处理。但线性分析法在对复杂资源进行处理时会受到一定的限制,从而影响特征提取效果。
对此,通过引入差分操作,设计基于差分Mel倒谱法的音乐旋律特征提取算法,能够捕捉到旋律中相邻帧之间的细微差异,旨在通过更加精细的音频处理技术,揭示旋律中的深层结构和内在规律。
1 音乐旋律特征提取算法
音乐旋律特征是指反映音乐中旋律结构和音高信息的特征。以下是一些典型的音乐旋律特征:
(1)音高:音高是音乐的基本要素之一,可以用数字表示,如音名或MIDI数值。
(2)音符持续时间:描述每个音符的时间长度,可用音符时值(如四分音符、八分音符等)表示。
(3)节奏性特征:包括节拍、速度、强弱等,可以通过计算音符间的时间间隔、音符的力度(loudness)等获取。
(4)旋律轮廓:描述音符的音高变化规律,如上升、下降、平稳等。
(5)音程:测量相邻音符之间的音高距离,如半音、全音等。
(6)旋律轮廓特征:通过计算音符之间的跳跃关系、音符位置等来捕捉旋律的轮廓特征。
(7)音乐模式:描述音乐中重复出现的旋律或乐句结构。
(8)转调特征:表示音乐中的调性变化,如调式变换、转调点等。
不同的特征对应不同的属性,需要设计不同的提取对象与提取方法。
1.1 音乐旋律加窗处理及基频提取
音乐旋律中的旋律特征由基础声音频率转换而来,音高曲线是音乐分析中至关重要的工具,它直观地展示了音乐旋律中音高随时间变化的趋势。音高曲线的形状、波动幅度和频率都包含着丰富的信息,可以揭示出旋律的轮廓、音高走势以及可能的情感表达。
通过分析音高曲线,音乐学家、作曲家或音频工程师可以捕捉到旋律的关键特征。例如,曲线的陡峭程度可以反映出旋律的起伏变化,而曲线的平滑程度则可能暗示着旋律的流畅性或连贯性。此外,音高曲线的极值点(如高点和低点)通常对应着旋律中的关键音符,这些音符在整个旋律中扮演着重要的角色。
在特征提取方面,音高曲线可以提供一系列有用的参数,如音高的平均值、中位数、方差、偏度等统计量,以及音高之间的时间间隔、音高变化的速率和方向等动态特征。这些特征可以被用于音乐分类、风格识别、旋律相似性比较等多种应用;同时,音高曲线还可以与其他音乐特征(如节奏、音色、和声等)相结合,以提供更全面的音乐分析。例如,结合音高曲线和节奏信息,可以分析出旋律的律动感和节奏特点;而结合音高曲线和和声信息,则可以揭示出旋律的协和性和和声色彩。对此,结合汉明窗函数对其进行加窗处理,结合差分Mel倒谱法,对基频进行提取,从而得到基频特征参数[5,6]。
考虑到音乐旋律的变化往往是在短时间内发生的,因此为了捕捉音频信号的局部特性,在进行加窗处理和分析之前,对其进行分帧处理。分帧处理需要将连续的音频信号划分为一些列短时的帧,对此需要对帧长以及帧移进行处理。帧长和帧移是分帧处理中的两个重要参数[7]。帧长定义了每个帧所包含的音频信号样本数,而帧移则决定了相邻帧之间的重叠程度。设定帧长为40毫秒,帧移为帧长的一半。根据确定的帧长和帧移,将音频信号分割成一系列帧。设音频信号为x(t),其中t表示时间,帧长为N,帧移为M,则第i帧的起始时间为ti,结束时间为ti+N。则第i帧的音频信号表示为x(ti+N)。对音频进行分帧处理,为了减少帧与帧之间的不连续性,采用汉明窗函数W(·)对其进行加窗处理,具体函数表达式如下所示。
其中,n代表帧内样本的索引,α代表分帧连续参数。通过对上述加窗处理后的帧数据进行余弦变换处理,得到每一帧的倒谱参数c(n),具体参数表达式如下所示。
其中,S(m)代表音乐旋律信号的对数能量。
具有复杂结构的音乐旋律通常会包含一定的动态特性,对此,采用Mel倒谱系数,通过模拟人耳的听觉特性,将声音信号的频谱转化为Mel频率标准的非线性形式,从而提取出音频的动态特性,并对该动态特性进行表征,由此得到的基频提取表达式如下所示。
其中,λi代表基频分辨率参数,k代表倒谱常数,c(n)代表基频动态线性变换函数。
对帧长以及帧移进行设定,实现基频分帧处理,并结合汉明窗函数对其进行加窗处理。
1.2 音高曲线获取
音高曲线反映了音乐旋律音高变化的趋势。通过分析音高曲线,捕捉旋律的轮廓和主要特征,为后续的特征提取和分类提供依据。因此,在完成基频提取之后,有必要提取音乐旋律中的音高曲线。
作为音高曲线的量化方法,音高向量包含旋律中每个音符的音高信息,以及它们之间的关系和变化。通过将连续的基音值转换为离散的矢量形式,可以更方便地进行计算和分析。
假设音乐旋律为MIDI格式,那么该文件下的音频信号通常由一段持续时间ti的连续音符值pi所构成,将音符值组成一个集合即为音符序列(p1,t1),…,(pi,ti),而音符的持续时间ti也等于分帧总数Fi。将任意音符pi表示为一维音高序列的形式,这个序列即为音高曲线,具体表达式如下所示。
对音高序列进行分帧处理,得到一组长度相等的音高向量。假设在音乐旋律基频中,每段音频对应的音高曲线为(p1,p2,…,pw),其中pw代表不同的音符值[8-10]。那么通过采用一个长度为h的时间窗对其进行分帧处理,得到一个固定的音高向量,并按照帧移参数对窗进行移动,从而得到同一窗内的新的音高向量[11]。通过采用上述操作,将音高序列进行遍历操作,直到时间窗超过了音高曲线的截止时间,得到音高向量的提取结果如下所示。
x=(p1,…,pw+T,pw+T(D-1))(5)
其中,x代表音高向量的提取结果,T代表时间窗的采样间隔,D代表音高向量维度。
通过将音频序列转换为一维的音高序列,并对序列进行分帧操作,得到音高向量信息,从而得到音乐旋律的轮廓以及主要特征。
1.3 音乐旋律特征提取
结合统计法,对音高区间的分布情况进行统计,从而获取音高统计特征,实现音乐旋律特征提取[12]。
对于一个特征提取基础单元S,假设该单元的长度为m,音高序列为(p1,p2,…,pm),为消除因音域差异带来的音高波动影响,需要对其进行归一化处理,具体处理公式如下所示。
其中,pmax和pmin分别代表音高序列中的最大值以及最小值。对于归一化后的每个音高向量,均有一个对应的区间统计数量ci,将其进行汇总,得到不同区间的音高统计信息(c1,c2,…,cS)。
虽然能够保证提取到的音乐旋律特征具有一定的稳定性,但是同时也会导致音乐旋律特征失去一定的区分性,即特征提取结果具有共通性,无法被准确区分[13],具体体现在:
(1)过度简化:过于简化音乐旋律的复杂性,导致特征过于通用,无法准确区分不同的旋律。例如,如果只考虑音频信号的基频(即主旋律的音高),而忽略了其他音符、节奏和和声信息,那么提取的特征就可能失去区分性。
(2)特征维度不足:如果提取的特征维度不足,即特征数量过少,导致特征的区分性不足。因为不同的音乐旋律可能在某些维度上具有相似性,但在其他维度上存在差异。如果只考虑少数几个维度,那么这些差异就可能被忽略。
(3)匹配局限性:不同的特征提取算法有不同的优缺点。单一算法在提取某些类型的特征方面更好,但其他类型特征的提取效果较差,与音乐的旋律特征不匹配,失去了可辨别性。
对此,为对上述问题进行优化,选择在上述的音高统计信息提取结果中加入一定区分性信息,具体包括音高均值、音高极差以及音高方差这三种指标,增加特征维度。考虑更多的音乐元素,如节奏、和声、音色等,以增加特征的维度。这样可以更全面地描述音乐旋律的特性,提高特征的区分性。具体求解表达式如下所示。
其中,Fsum代表音乐旋律多维特征提取结果。
结合音高区间的分布情况统计结果,并在其中加入一定的区分性信息指标,得到音乐旋律的多维特征。
2 实验
所选取的音乐数据库是一个综合性的音乐收藏库,音乐数据库采用关系型数据库管理系统,确保数据的稳定性和安全性。数据库的核心结构由多个表组成,每个表代表音乐库中的一个实体,如“艺术家”“专辑”“歌曲”等。这些表通过关系键相互连接,形成了完整的数据库结构,具体结构如表1所示。
基于表1,将连续的模拟音频信号转换为离散的数字信号。设定采样率为44.1kHz,并对量化位数进行设定。这决定了每个采样点的精度,通常以位(bit)为单位。常见的量化位数有16位和24位。16位量化通常足以提供高质量的音频,而24位则提供了更高的动态范围和精度。将量化位数调整为24位,使用FFmpeg软件,读取原始音频文件,并将其转换为指定采样率、量化位数和声道数的数字音频数据。
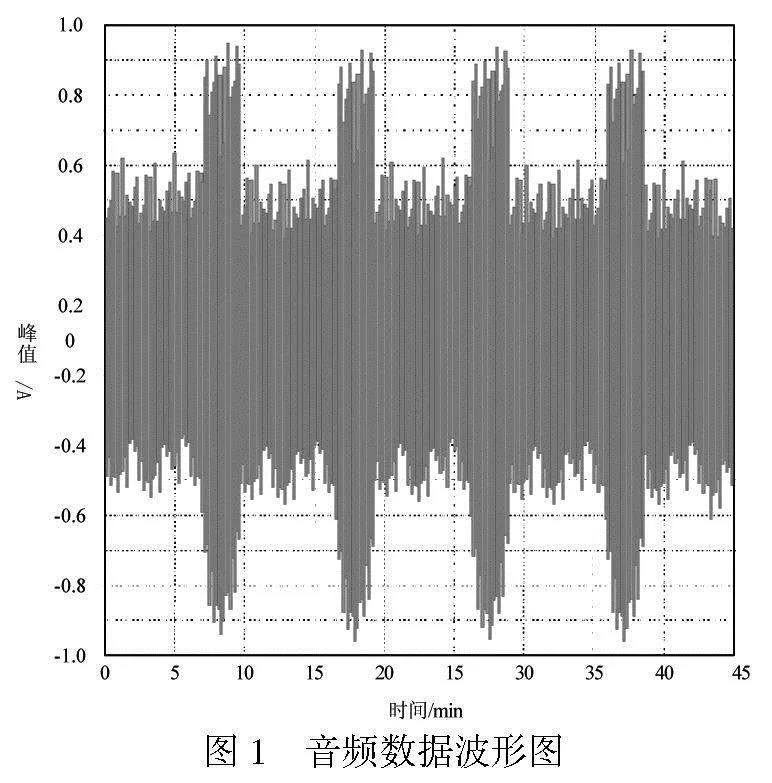
通过读取音频文件的元数据,确保每个音频文件的时间戳保持一致,从而完成音频对齐处理。在完成音频预处理后,得到部分音频数据波形图如图1所示。
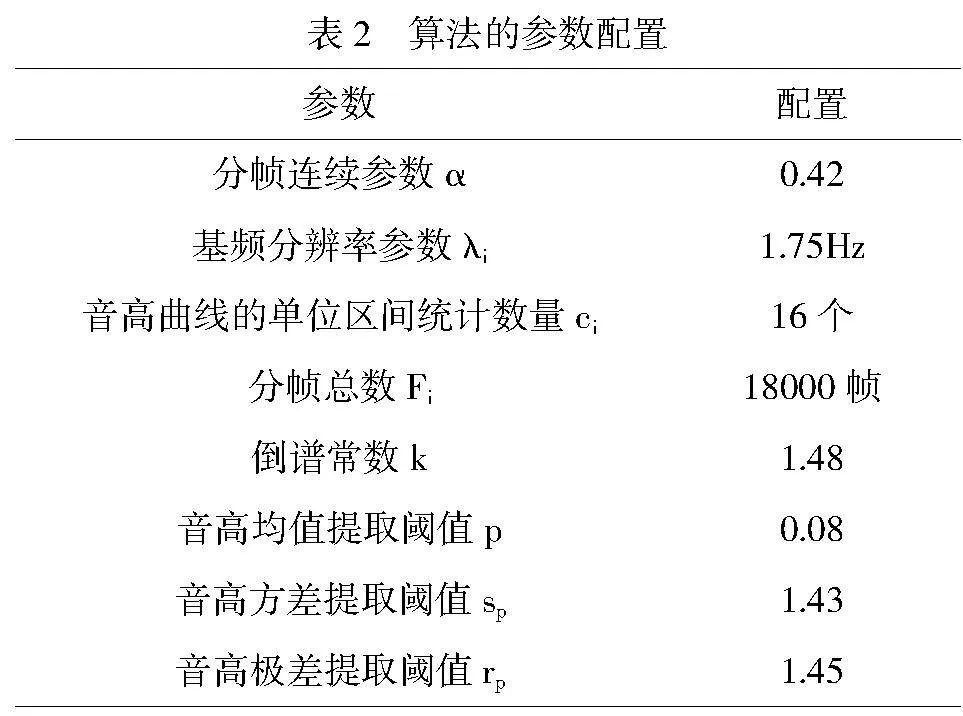
选取了两组常规的音乐旋律特征提取算法作为对比对象,分别为基于数据融合的音乐旋律特征提取算法,以及基于深度学习的音乐旋律特征提取算法,具体配置情况如表2所示。
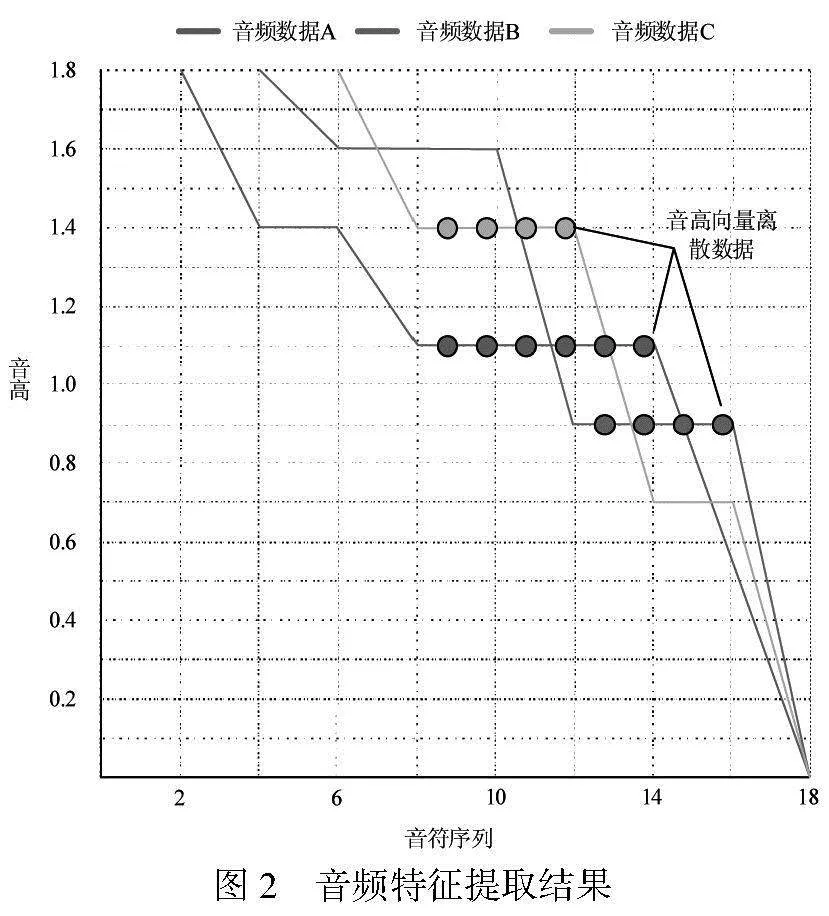
对原始数据集中的音频数据旋律结构进行了记录,并针对三种提取结果中的旋律特征结构进行了调取,从而得到了一份旋律特征结构对比结果。音频特征提取结果如图2所示。
由图2可知,针对不同的音频数据进行特征提取,本文提出的方法获得了音高曲线以及离散的音高向量数据。
以不同提取结果下的旋律结构相似性指数(SSIM)作为对比指标,用于衡量不同方法的提取效果。该指数的具体计算公式如下所示。
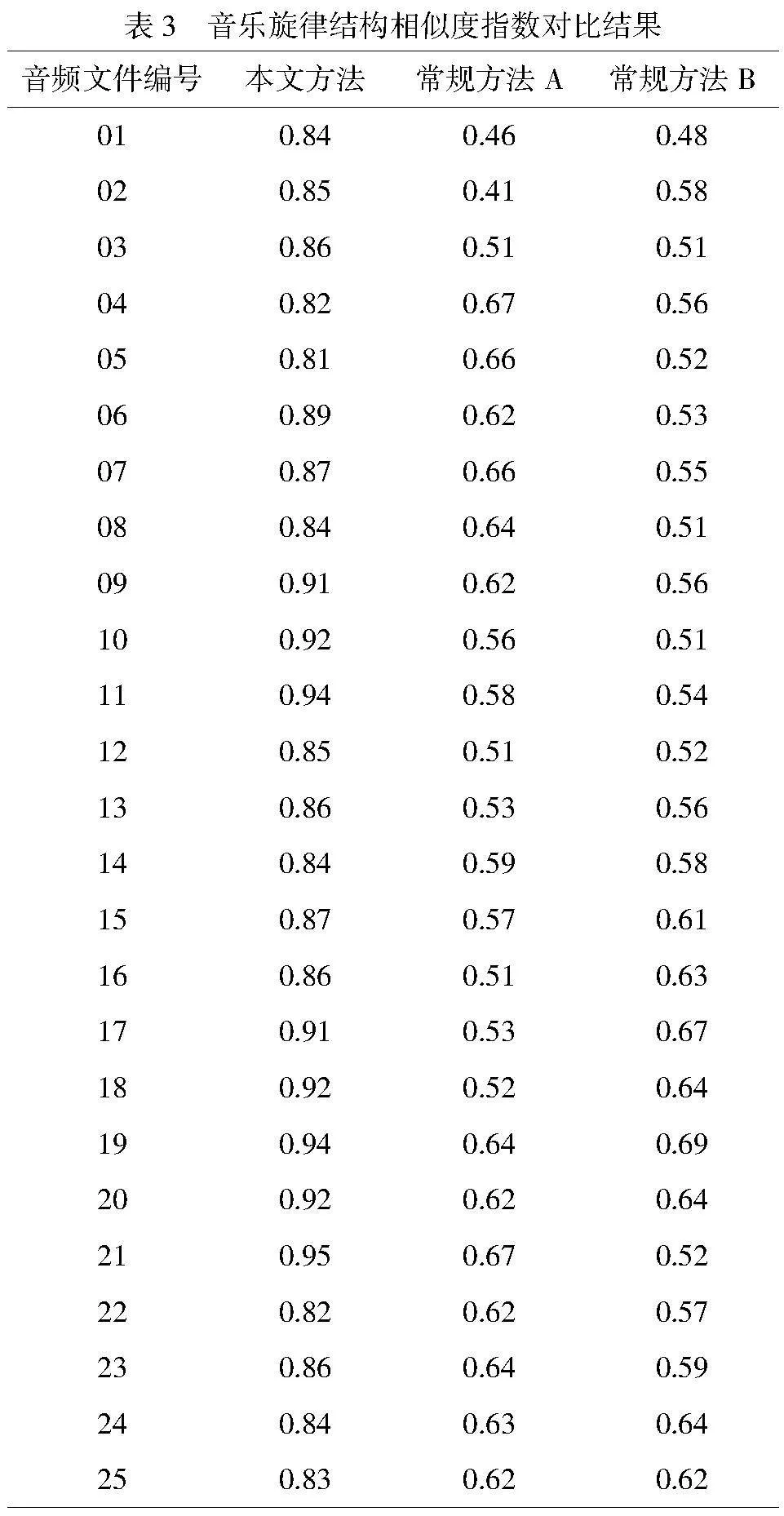
其中,wi代表权重参数,pi代表音符序列,δi代表频谱参数,s(x,y)代表结构相似度判断函数。不同方法下的旋律结构相似性指数对比结果如表3所示。
由表3可知,在针对相同的音频数据进行特征提取时,不同方法的提取结果均有所不同。本文提出的方法在特征提取效果方面明显优于其他方法,提取结果的旋律结构与原音频的旋律结构具备较高的相似度。
3 结束语
本文设计了一种基于差分Mel倒谱法的音乐旋律特征提取算法,通过音乐旋律加窗处理及基频提取,提取音乐旋律中的音高曲线,结合统计法,对音高区间的分布情况进行统计,从而获取音高统计特征,获得了音高曲线以及离散的音高向量数据,保证了提取后的旋律结构与原音频的旋律结构具备较高的相似度。但是该算法在处理不同音乐风格和文化背景的音乐时,其泛化能力仍有待提高。为了克服这些局限性,在今后的研究工作中,将进一步挖掘旋律特征的深层次信息,提高特征提取的准确性和鲁棒性。
参考文献:
〔1〕何丽,刘浩.一种基于多特征融合与压缩激励模型的音乐主旋律提取算法[J].计算机应用与软件,2023,40(05):160-166+261.
〔2〕杨汶雯,石梦荧.基于深度学习的音乐特征提取及流派分类[J].长江信息通信,2021,34(05):9-11.
〔3〕ZHANG J W. Music feature extraction and classification algorithm based on deep learning[J]. Scientific Programming, 2021, 2021: 1651560.
〔4〕ZHANG K D. Music style classification algorithm based on music feature extraction and deep neural network[J]. Wireless Communications and Mobile Computing, 2021, 2021: 9298654.
〔5〕王昊,刘渊晨,赵萌,等.基于多模态特征的音乐情感多任务识别研究[J].现代情报,2022,42(11):61-75.
〔6〕张李明,洪蕾.基于双阈值函数的音符检测旋律时间序列化分析[J].电子技术,2022,51(09):22-25.
〔7〕常凤,徐小华,胡忠旭.基于贝叶斯判别法对音乐特征信号的分类研究[J].电脑知识与技术,2022, 18(13):79-81.
〔8〕王宁,陈晨,陈德运,等.哼唱检索中旋律特征的聚类与优化方法[J].哈尔滨理工大学学报,2022,27(01):61-68.
〔9〕倪嘉惠,金文清,黄荣,等.基于顶层反馈和联合检测的主旋律提取算法[J].计算机应用,2021,41(S2):103-107.
〔10〕任瑞.基于音频特征的音乐音符智能切分识别方法[J].信息技术,2021,45(12):31-36.
〔11〕王力,王鑫,谢凌云.音乐信号处理的特征分析综述[J].中国传媒大学学报(自然科学版),2021, 28(06):59-72.
〔12〕张岩,刘哲.基于CQT的乐器独奏单旋律的提取[J].沈阳师范大学学报(自然科学版),2021,39(05):465-469.
〔13〕牛育谦,杨艺媛.基于谐波结构的民族乐器音色特征提取[J].自动化与仪器仪表,2023,43(04):34-38.
〔14〕余程年,杜梦丽,吴其林,等.基于多级度量学习的细粒度旋律相似判别算法[J].绥化学院学报,2023,43(03):147-152.

