基于干扰信号剔除的全频段音乐和弦识别方法

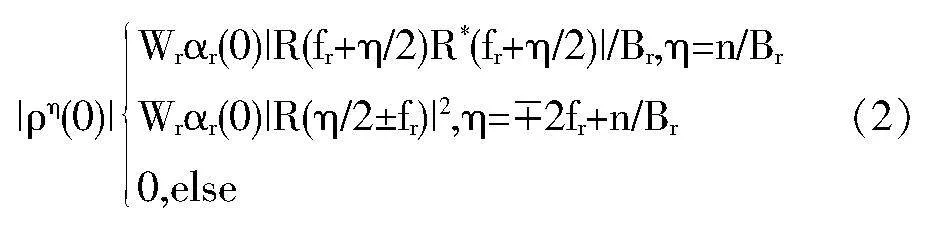
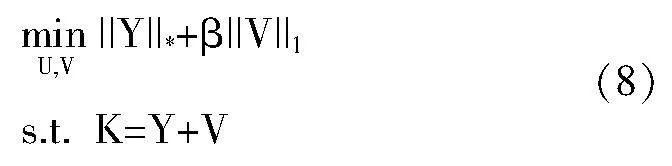
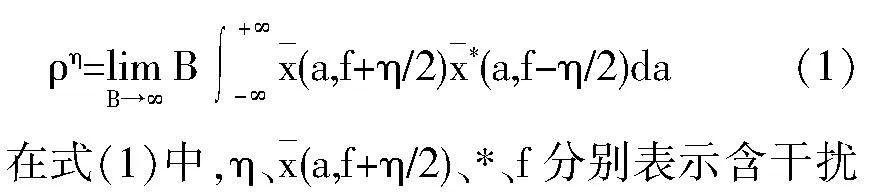
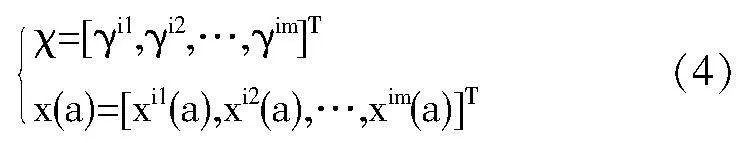
摘 要：为避免音乐信号中干扰信号造成的影响，实现更准确的和弦识别，提出一种基于干扰信号剔除的全频段音乐和弦识别方法，对全频段音乐信号进行采集，利用自适应频移滤波器剔除音乐信号中的干扰信号后，通过傅里叶变换和音阶映射提取干扰信号的全频段音乐信号PCP（Pitch Class Profles）特征，构建和弦PCP特征模板库，并通过稀疏表示分类器表征提取的待识别的全频段音乐信号PCP特征与和弦PCP特征模板库之间的线性关系，实现全频段音乐和弦识别。通过实验验证，该方法能够实现一种较为精准的全频段音乐和弦识别，对于不同和弦识别率均较高，均能保证在95%以上，且平均识别时间较短，能够保证在3ms之内。

关键词：干扰信号;全频段音乐;和弦识别;自适应频移;滤波器;音阶映射

中图分类号：TP391 文献标识码：A 文章编号：1673-260X（2024）09-0064-06

全频段音乐和弦识别在音乐制作、学习及智能音乐推荐等领域具有广泛的应用和关键性作用[1]。在音乐制作过程中，通过识别全频段音乐和弦，制作人可以更好地理解音乐的和声结构，从而进行更加精确的音乐编曲和混音。并且在音乐教育领域，全频段音乐和弦识别技术可以作为教学辅助工具，帮助学生快速识别和理解音乐作品中的和弦结构。作为音乐自动处理的核心要素之一，它在推动音乐领域的发展中发挥着不可或缺的作用，对提升音乐制作效率、优化音乐学习体验以及改进音乐推荐精度都具有重要意义[2]。

黎思泉等人提出了一种创新的乐曲和弦识别方法，该方法依托于生成对抗网络的多基频估计算法。该方法首先采集音乐信号，并运用谐音指纹图精细提取音符段的频谱特征。随后，构建一个卷积神经网络模型，该模型能够有效识别音乐中的主导基频。在此基础上，将已识别出的主导基频视为后续基频识别的潜在干扰因素，通过生成对抗神经网络精准去除这些干扰项，进而进行新的多基频估计。该方法采用逐级迭代的方式，完成和弦的多基频估计，最终实现和弦的精准识别[3]。但在音乐信号采集过程中，可能会受到各种噪声、失真或其他环境因素的0tZ4fx4PtidTmc0XEgLiMg==干扰，这些因素都可能影响到谐音指纹图对音符段频谱特征的提取，进而影响和弦识别的准确性。张珺等人设计了一种基于优化小波变换和神经网络的电子音乐信号识别方法，将采集的音乐信号进行处理，对音乐信号中的低、高频系数进行扩大处理，从而实现小波降噪操作，通过多输入输出神经元实现前向径向基函数神经网络构建，并通过将高斯激活函数对隐藏层神经元进行替换，从而得到成中心径向堆成形式分布的音乐信号，对过程中的连接权值进行求解，实现音乐信号中的和弦自动识别[4]。虽然通过扩大音乐信号中的低、高频系数可以实现小波降噪操作，但这种方法可能无法完全去除所有噪声。特别是在噪声成分复杂或噪声水平较高的情况下，降噪效果可能不够理想，这会影响后续和弦识别的准确性。Bando Y等人提出了一种音乐和弦识别方法，该方法首先对音乐信号进行采集，通过对采集的音乐信号的声音频谱中提取标准化音符数，建立声音频谱的数据库，并将提取得到的标准化音符数与数据库中生成的音符数之间进行对比，得到相似性，进而实现音乐中的和弦识别[5]。对于实时音乐处理或在线识别应用，需要面临计算复杂度和实时性的挑战。在处理大量音乐信号或复杂和弦结构时，该方法能力较弱，实现的识别结果的准确性和可靠性较差。

通过剔除干扰信号，可以有效降低数据处理量，进而提升处理效率，使得音乐中的和弦识别更为精准[6]。这种方法在复杂的音乐环境中仍能维持出色的识别性能，展现出强大的鲁棒性。对于推动音乐自动处理技术的不断进步，这一方法具有不可忽视的重要意义。因此本文提出了一种基于干扰信号剔除的全频段音乐和弦识别方法，实现较为精准的和弦识别，为音乐分析提供了较好的技术支持。

1 全频段音乐和弦识别方法

从全频段音乐中实现和弦识别是一种音乐信号的处理过程，实现和弦识别的过程如图1所示。

如图1所示，进行全频段音乐声音信号采集后，干扰信号剔除成为关键步骤，干扰信号剔除旨在有效去除噪声等干扰信号。这一环节至关重要，能够为后续和弦识别提供高质量的原始声音信号，从而确保和弦识别的效果更为精准。

1.1 全频段音乐干扰信号剔除

首先需要对全频段音乐以44 100Hz的采样率进行音乐信号采样，得到一个含干扰的全频段音频信号x（a），长度为d。则该音频信号的循环谱密度函数表示为：

音频信号的循环频率、全频段含干扰音频信号中所有信号的平均加权、复共轭、含干扰音频信号频率、含干扰音频信号比特时间宽度。

则以f=0为特征面，能够得到含干扰音频信号的循环谱密度函数为：

其中，分别用αr（0）、R（ ）、R*（ ）表示含干扰音频信号中干扰信号的自相关函数、单周期内循环结果及其复共轭;Wr表示干扰信号功率;fr表示干扰信号频率;n为常数，n=1，2，…N，Br表示干扰信号数据比特时间宽度。

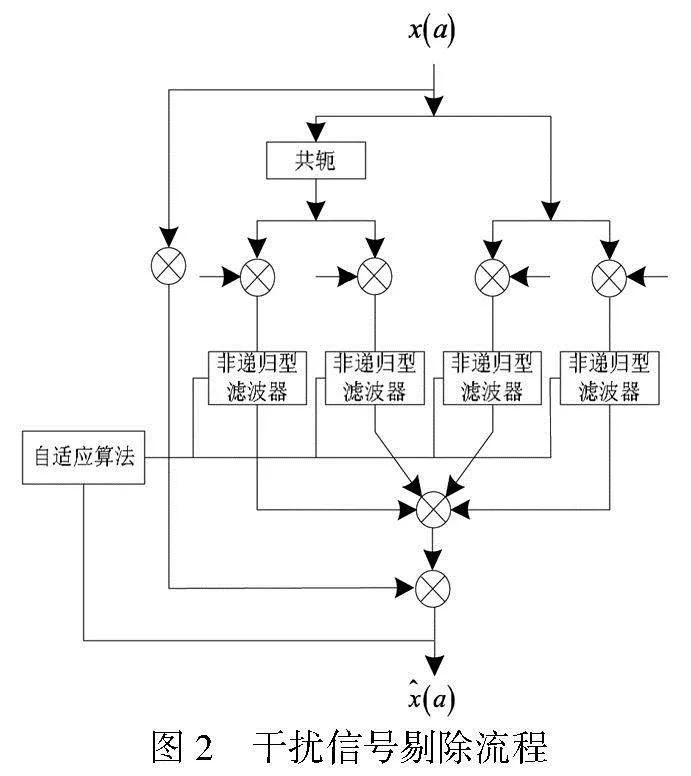
上述过程能够得到含干扰全频段音乐信号中的干扰信号，需要对其进行剔除，可以通过自适应频移滤波器实现[7]。实现干扰信号剔除的过程如图2所示。

由图2可知，自适应频移滤波器内部存在多个非递归型滤波器。分别用η、ε表示干扰信号的非共轭、共轭循环频率，vr′、f′表示干扰信号的码速率和频率。利用非递归型滤波器实现干扰信号剔除，该过程通过引入循环频率为κ的参考信号τ（a），最终得到剔除干扰的全频段音乐信号（a）。

通过构建误差目标期望函数，以获得最佳自适应频移滤波器系数，保证剔除干扰信号的效果，目标期望函数由式（3）表示。

Q{τ（a）-r′（a）2}=Q{τ（a）-χχ（a）2}（3）

在式（3）中，r′（a）、χχ分别表示重构的音乐信号中的干扰信号和非递归型滤波器系数向量的共轭转置。

位于非共轭支路的滤波器存在的关系如式（4）所示。

式（4）中，分别用γi1，γi2，…，γim、T表示非递归型滤波器支路系数、转置运算。

通过最小平方误差计算得到最佳非递归型滤波器系数向量和重构的音乐信号干扰信号[8]，表示为：

式（5）中，分别用δ、λ表示迭代收敛因子、自适应频移滤波器系数向量的参数。

1.2 音乐信号PCP特征提取

K=L·I（6）

其中，L表示傅里叶变换矩阵，大小为p×p。

设频谱中和弦对应的音阶基频和其谐波成分表征的矩阵为Y，V为人声等信息组成的非谐波成分，则存在：

K=Y+V（7）

引入折中因子β>0，则存在：

式（8）中，|| ||1表示一范数运算，描述了矩阵的稀疏程度。依据增广拉格朗日乘子法能够进行计算，得到最佳的谐波频谱矩阵Y。

通过音阶映射实现音频分帧信号的谐波频谱矩阵转换为12维PCP特征的过程[10]。PCP特征指音高类别轮廓，表征音乐信号中不同音高分布情况。转换过程表示为：

C=Z·Y（9）

其中，分别用C、Z表示RPCP色度矩阵、映射矩阵，RPCP是改进的音高类别轮廓特征提取方法。映射矩阵表示为：

其中，μ（ ）表示映射函数，映射矩阵Z本质上为变换矩阵，能够描述频谱矩阵Y和RPCP色度矩阵C之间的变换过程[11]。用2πωi（0≤i≤p-1）、fb（1≤b≤12）表示频谱变换之后的频谱各频段频率和12个音阶的基频。

由于定义其他音符频率基准的C4音符对应的频率为fC4=261.626Hz，因此能够得到各音符对应的频率fb，通过式（11）表示。

fb=2e/12fC4（11）

式（11）中，e表示C4音符与各音符之间的音程差。最终得到的映射矩阵函数μ（s，fb），通过式（12）表示：

式（12）中，将s表示为全频段音频信号实现变换后的各频率成分。

通过将式（10）、式（11）、式（12）带入式（9）中，最终能够得到和弦PCP特征矩阵Y，该矩阵实现了有效的音频信号频谱能量压缩，是音频信号和弦中的一种关键特征。

1.3 基于稀疏表示分类器的全频段音乐和弦识别

将2.2小节中得到的PCP特征输入到稀疏表示分类模型中，实现音频信号中的和弦识别。稀疏表示分类能够将和弦识别过程视为寻找系数向量的过程，该稀疏向量表征了待识别的和弦与和弦模板库中的最佳线性关系，即待识别的和弦PCP特征如果属于和弦PCP特征模板库中的某一类[12]，则对该和弦PCP特征的线性组合表示中，只包括该类和弦PCP特征[13]。其中，线性表示系数向量是稀疏的，因此需要稀疏表示分类算法实现和弦识别。

（1）稀疏表示方法。设和弦PCP特征模板库中类别数量为φ，通过Uσ=[uσ，1，uσ，2，…，uσ，ξσ]∈Rζ×ξσ表示第σ类和弦PCP特征，ξσ表示第σ类和弦PCP特征的数量，ζ表示和弦PCP特征集的维度。则φ个和弦PCP特征类别组成的和弦词典矩阵表示为：

U=[U1，U2，…，Uφ]=[u1，1，u1，2，…，uσ，ξσ]（13）

设待测的和弦PCP特征Y属于和弦PCP特征模板库中的第ψ类，则和弦词典矩阵U构成的空间线性表示为：

v=aY，v∈Rζ（14）

式（14）中，a=[0，…，0，ak1，ak2，…，akξk，0，…，0]T∈Rζ，由于待测和弦PCP特征Y只能通过和弦PCP特征模板库中与待测和弦PCP特征相关的和弦PCP特征线性表示，因此v的解是稀疏的[14]。

（2）由于v的解是稀疏的，根据压缩感知和稀疏表示，v的解可通过最小范数得到[15]，表示为：

a1′=argmin||a||1（15）

其中，将a的近似解表示为a1′。

（3）在稀疏表示分类模型构建中，可能存在误差影响，可能导致分类的结果存在偏差，为实现精准的和弦识别，引入新向量0（a1′），其非零元素仅是a1′与第o类和弦相关的成分，则和弦v识别方法表示为：

F（v）=argmino（v-Y0（a1′））（16）

通过以上过程，实现全频段音乐和弦识别的具体过程为：

（1）首先对和弦模板库中所有的和弦样本进行PCP特征进行提取，计算该时间范围内的PCP特征的平均值，将得到各和弦的12维向量组合，作为和弦PCP特征模板库。

（2）提取待识别和弦的PCP特征，将其输入到稀疏表示分类模型中进行识别。

（3）通过式（15）、式（16）进行稀疏表示分类模型的识别计算，得到的分类结果即为该待测和弦的识别结果。

2 实验与分析

为全面验证本方法在全频段音乐和弦识别方面的效果，选取各大网络音乐平台的音乐作为原始声音数据。这些数据涵盖了不同风格、流派和复杂度的音乐，以确保验证过程的广泛性和代表性，通过图3所示的实验过程进行验证。

在实验中，声音采集通过ECM-VG1麦克风实现，该麦克风能够实现较为清晰自然的声音采集，从而能够为后续的实验提供较为良好的原始声音信号。ECM-VG1麦克风具体的参数如表1所示。

通过上述的设备进行声音采集，能够实现后续的全频段音乐和弦识别。

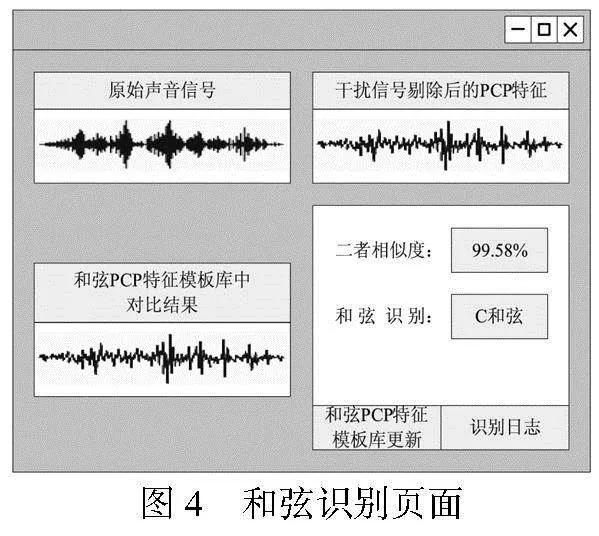
通过本文方法能够实现和弦识别的页面如图4情况所示。

由图4可知，通过本文方法能够实现一种较为精准的和弦识别，这一方法不仅能够对原始声音信号进行全面的处理，有效地剔除音乐中的干扰信号，确保信号的纯净性，而且还能够通过对比和弦PCP特征模板库中的和弦，实现对不同和弦的精确识别。这一过程的实现，不仅提升了音乐识别的准确性，也为后续的音乐分析和处理提供了有力的支持。由此验证了本文方法在音乐处理领域具有广泛的应用前景，对于推动音乐技术的发展和进步具有重要意义。

为验证本文方法实现和弦识别的有效性，通过不同的和弦对本文方法进行验证，得到的本文方法实现的检测情况如表2所示。

由表2的数据结果可知，本文方法展现出了相当高的准确性，其识别出的和弦与实际和弦结果高度吻合。这一方法不仅成功地对常见的C和弦、F和弦和E和弦进行了精准识别，还对于较为复杂的增三和弦（如Caug和弦）和减三和弦（如Bdim和弦）同样展现出了出色的识别能力。这种精准识别的能力，为音乐创作、演奏以及音乐分析提供了有力的支持。

以C和弦为例，通过本文方法对该和弦进行识别，将本文方法与和弦识别中常用的规则法和支持向量机法实现的和弦识别效果进行对比，得到的对比情况如图5所示。

由图5可知，C和弦是由D、E、G音阶组成。传统的规则法和支持向量机法在实现和弦检测时，往往不能精准地识别出和弦的种类。这些方法在处理某些复杂的和弦结构时，容易出现误差，导致与实际和弦相差较大。而通过本文所提出的和弦识别方法，我们能够实现一种相当精准的和弦识别，其识别结果与实际的和弦频率基本保持一致。这种方法不仅准确度高，而且在处理复杂音乐结构时也能保持稳定的性能。

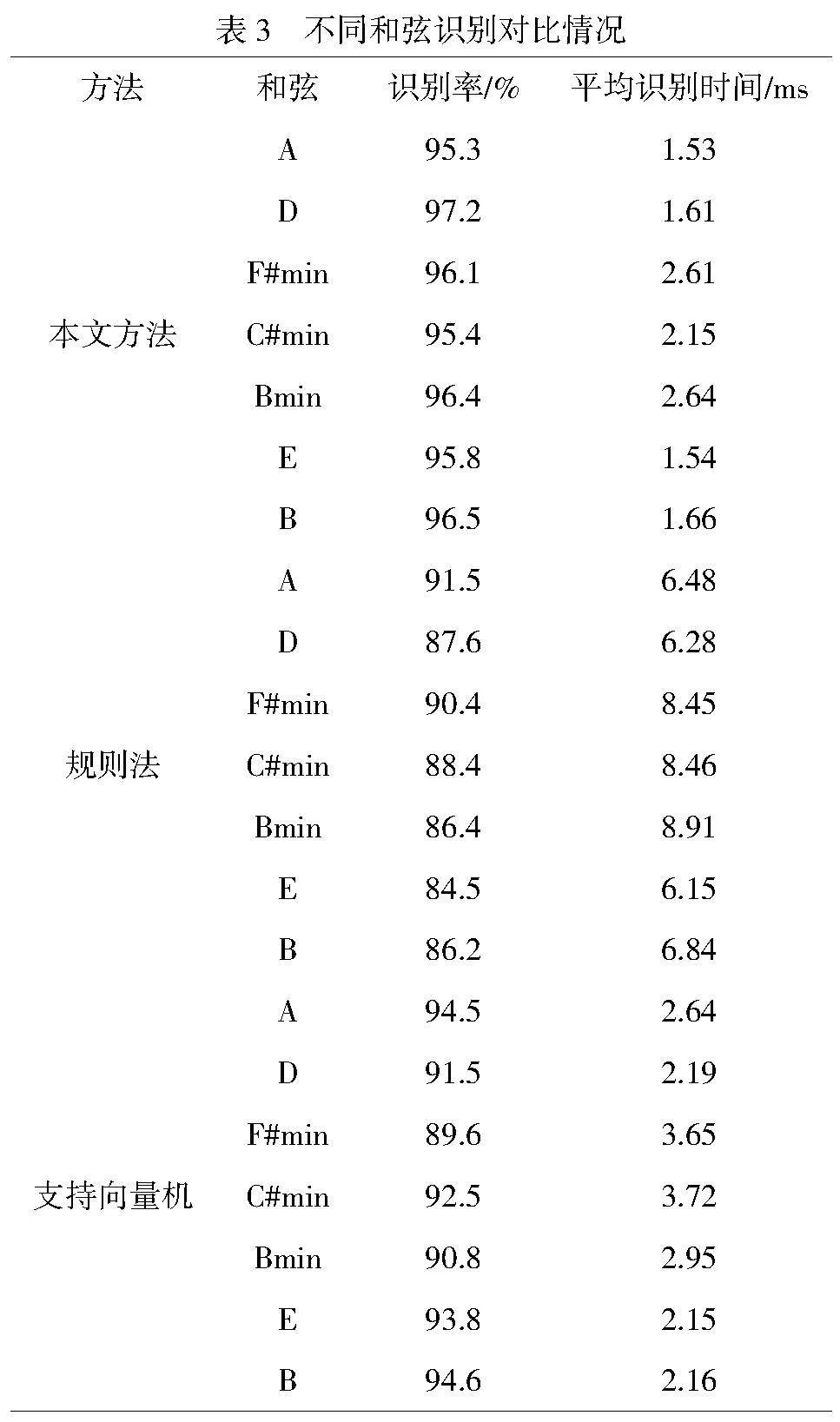
为了深入验证本文所提出和弦识别方法的有效性，对比了本文方法与规则法和支持向量机法的和弦识别效果。具体对比内容包括不同和弦的识别率以及平均识别时间，详细对比数据如表3所示。

由表3可知，3种方法对于不同的和弦识别效果存在差异，通过对3种方法进行对比可以看出，本文方法实现的不同和弦识别率较高，均能保证在95%以上，且平均识别时间较短，能够保证在3ms之内，是一种识别率较高，识别时间较短的方法，为后续的音乐分析提供了较好的技术手段。

3 结论

本文提出了一种基于干扰信号剔除的全频段音乐和弦识别方法，通过精细过滤音乐信号中的噪声、回声等非目标成分，极大地提升了和弦识别的精准度和稳定性。该方法凭借先进的信号处理技术，能够精确识别和剔除干扰信号，确保音乐信号中关键的音符与和声信息得以保留。在实际应用中，该方法展现出了出色的鲁棒性，即使面对复杂多变的音乐环境，也能维持高水平的识别性能。总体而言，该方法在音乐自动处理领域具有广泛的应用前景，为音乐制作、学习及推荐等领域提供了强有力的技术支撑。

参考文献：

〔1〕胡嘉健，廖尚頔，陈霏.音阶法和弦表征方式对于和弦生成任务的影响[J].中国传媒大学学报（自然科学版），2023，30（03）：1-7.

〔2〕朱雨晨.简谱符号的特征识别[J].信息与电脑（理论版），2022，34（10）：199-202.

〔3〕黎思泉，万永菁，蒋翠玲.基于生成对抗网络去影像的多基频估计算法[J].计算机科学，2022，49（03）：179-184.

〔4〕张珺，赵玉霞.基于改进小波变换及神经网络的电子音乐信号识别方法[J].自动化技术与应用，2023，42（05）：48-51.

〔5〕Bando Y， Tanaka M. A Chord Recognition Method of Guitar Sound Using Its Constituent Tone Information[J].IEEJ Transactions on Electrical and Electronic Engineering，2022，17（01）：103-109.

〔6〕黄琴，兰小机，夏益强，等.Chan-IDW算法在信号干扰下的UWB精确定位研究[J].电子测量技术，2023，46（09）：1-7.

〔7〕刘明，丘聪，佳沐.基于快速FIR算法的自适应滤波器的VLSI实现[J].河南科技，2023，42（09）：15-18.

〔8〕王秋莎，张峥，王磊，等.最小均方自适应滤波器设计及性能影响因素分析[J].河北电力技术，2023， 42（03）：51-55.

〔9〕韩彬彬，程科，王义军.基于CGABC-SVM的多特征融合音乐分类算法研究[J].计算机与数字工程，2023，51（04）：820-825.

〔10〕周宇航，侯进，李嘉新，等.基于频域叠加和深度学习的频谱信号识别[J].计算机应用研究，2023， 40（03）：874-879.

〔11〕王源，冯永新，钱博.一种循环谱特征提取的直扩信号智能识别方法[J].沈阳理工大学学报，2023，42（04）：31-39.

〔12〕王赛男，郑雄风.基于稀疏字典表示的无监督域适应学习算法[J].计算机应用与软件，2023，40（07）：311-318.

〔13〕李永豪，胡亮，高万夫.基于稀疏系数矩阵重构的多标记特征选择[J].计算机学报，2022，45（09）：1827-1841.

〔14〕佘学兵，熊蕾，黄丽，等.基于长短期记忆的稀疏数据过滤推荐算法[J].计算机仿真，2023，40（02）：395-398+523.

〔15〕章涛，张亚娟，孙刚，等.稀疏贝叶斯字典学习空时机动目标参数估计算法[J].电子与信息学报，2022，44（08）：2884-2892.