不同节理层对砂岩力学特性影响的数值模拟研究

摘 要：砂岩是隧道工程中常见的岩体，富含节理面，节理面通常对岩体的力学特性影响较大，为保证隧道工程施工安全，需要了解层状砂岩的力学特性，为隧道建设提供理论支撑。该文为探明不同节理层对岩石力学特性进行数值模拟研究，以不同节理厚度、不同节理层数为研究变量，基于Holmquist-Johnson-Cook（HJC）本构模型，结合有限元数值模拟软件ANSYS/LS-DYNA，开展不同节理层对岩石力学特性的数值模拟研究，为类似层状砂岩的研究提供参考。

关键词：节理砂岩；数值模拟；HJC本构模型；力学特性；隧道工程

中图分类号：TU45 文献标志码：A 文章编号：2095-2945（2024）31-0067-04

Abstract： Sandstone is a common rock mass in tunnel engineering. It is rich in joint surfaces. The joint surfaces usually have a great impact on the mechanical characteristics of the rock mass. In order to ensure the safety of tunnel engineering construction， it is necessary to understand the mechanical characteristics of layered sandstone to provide theoretical support for tunnel construction. In order to find out the numerical simulation research on the mechanical properties of rock by different joint layers， this paper takes different joint thicknesses and different joint layers as research variables， based on the Holmquist-Johnson-Cook （HJC） constitutive model， combined with the finite element numerical simulation software ANSYS/LS-DYNA， carries out numerical simulation research on the mechanical properties of rock by different joint layers， providing reference for the study of similar layered sandstones.

Keywords： jointed sandstone; numerical simulation; HJC constitutive model; mechanical properties; tunnel engineering

砂岩作为一种普遍发育的岩体，在我国各地均有分布，其在形成过程中受到沉积作用影响，一般都有明显的层理构造，节理层的存在使岩石整体力学性能产生一定变化，对于隧道工程中防灾减灾具有重要意义[1-2]。有限元数值模拟是研究岩石力学性能问题的常用方法[3]。因此，研究不同节理层对砂岩的力学特性具有十分重要的工程意义。

国内外学者针对岩石的节理开展了大量研究工作。席道瑛等[4]基于广义胡克定律对层状砂岩的各向异性进行了研究。高春玉等[5]对层理砂板岩开展了单轴和三轴试验，对砂板岩的强度特性及各向异性进行了深入研究。邓华锋等[6]基于现有的岩体巴西劈裂成果，研究了不同节理角度层状砂岩的抗拉强度。陈新等[7]制作了一种石膏试件，用于代替不同节理情况的预裂隙岩石，并对制作的石膏试件开展了单轴压缩试验，揭示了随着裂隙连通率的增大，岩石的延性得以增大。李海波等[8]通过在岩石试件的端面增加混凝土层，揭示了岩石在不同剪切速率下层理倾角对岩石强度的影响。谢财进等[9]通过分析岩石的临界损伤值，揭示了层状白云岩的损伤规律。郝志斌等[10]通过对不同倾角节理砂岩的单轴压缩数值模拟，研究了砂岩的能量演化规律，同时揭示了节理分布及非均匀性对其影响。卢玲等[11]对2种不同节理角度的板岩开展了大量循环载荷试验，研究了循环载荷下的板岩变形特征。黄叶宁等[12]以典型节理岩体为研究对象，通过调整水压大小、干湿循环的方式，研究了经典节理岩体的剪切力学特性，并提出了一种节理岩体的剪切本构模型。周文海等[13]通过建立节理岩体数值模型，利用应力波的波动理论与能量密度理论，揭示了应力波的传播规律，并对爆炸产生的裂纹、裂隙进行了系统性的分析研究。

当前研究多集中于岩体的节理倾角对岩石力学特性、损伤规律的影响，并获得了大量成果。但对于节理的厚度和层数研究鲜有报道。因此，本文以贵州省开州湖大桥为工程依托，以不同节理层厚度、不同节理层层数为变量，开展了SHPB数值模拟研究，揭示了节理变化对岩石的力学特性影响规律。研究结果可为相关岩石节理研究提供参考。

1 HJC本构模型

HJC本构模型相较于传统的KC本构模型，屈服应力变化因综合考虑了材料的损伤、应变效应及静水压力，能全面且准确地描述材料的应变率特性，目前被大量学者应用于岩石的冲击动力学中。

1.1 强度模型

HJC本构模型的强度模型使用标准化等效应力对强度进行描述，强度公式为

σ*=A1-D+BP *N1+C lnε*≤Smax ，（1）

式中：σ*为标准化等效应力，σ*=σ/fc；σ为实际等效应力；fc为材料的单轴抗压强度；A为标准化黏聚力强度；D为损伤因子；Smax为标准化等效应力的最大值；B为标准化压力硬化系数；P *为标准化压力；ε*为标准化应变率；N为标准化硬化指数；C为应变率影响系数。

在天然条件下通常忽略损伤、应变率和温度的影响，可简化为

σ*=A+BP *N≤Smax 。 （2）

1.2 损伤模型

HJC损伤模型包含塑性应变和体积压缩塑性应变两部分，损伤变量D公式为

式中：？驻？着p为一次循环过程中单元体的等效塑性应变；？驻？滋p为一次循环过程中单元体的等效塑性体积应变增量；T *为标准化抗拉强度，T *=T/fc（T为抗拉强度）；D1和D2为材料的损伤参数。

1.3 状态方程

HJC状态方程为体积应变与静水压力的函数，方程分为3个阶段。第1阶段为线弹性阶段，此时静水压力P≤Pcrush，材料处于线弹性状态为

P=K？滋 ， （4）

式中：K为体积模量；？滋为体积应变。

第2阶段为塑性过渡阶段，此时静0406da3815ba7977b417ef295d81fac8203982244ff65b6fe50fe9e0b90cc2b4水压力Pcrush＜P＜Plock，材料处于塑性状态，材料内部的空隙被压缩破坏，产生塑性体积损伤。

第3阶段为高压缩阶段，此时静水压力P≥Plock，此时材料内部的空隙基本已被全部压缩，岩体开始收缩，此区间内状态方程为

， （5）

式中：K1、K2、K3为压力常数；为等效体积应变。

2 有限元模型的建立

本文以霍普金森压杆测试系统ALT100试验系统为原型建立模型。试验系统由控制部分、试验部分和数据采集部分组成，由于数值模拟过程中能监测任意单元体，本文仅对试验部分进行数值模拟，试验部分由撞击杆、入射杆、岩石试样和透射杆组成。试验系统基本参数见表1。

为使数值模拟尽可能还原室内试验过程，本文所建立的岩石样品模型尺寸取值为实际试验标准岩石样品尺寸，具体尺寸为φ50 mm×25 mm。选用Hypermesh2021软件建立SHPB冲击数值模型，定义岩石样品模型的网格尺寸为0.5 mm，岩径向划分50份。为节约计算时间和储存空间，且撞击杆、入射杆和透射杆对精度要求不高，定义其网格尺寸为5 mm，沿径向划分400份。模型建立如图2所示。

为研究不同节理厚度、不同节理层数节理对岩石力学特性的影响，本文设计了不同节理层厚度的单层节理岩石试样，节理厚度分别为1、3、5、7 mm；不同节理层数的等间距模型，节理层数分别为2、3、4层，节理层厚度均为1 mm。

通过修改K文件为模型中各部件进行赋值，使用表1中的参数为撞击杆、入射杆、透射杆赋值。初始速度以等位移加载的方式为撞击杆添加，初速度为20 m/s。考虑室内试验及岩石材料的特点，使用有限元数值模拟软件自带的接触关键字CONTRACT_AUTOMATIC_SURFACE_TO_SURFACE用于撞击杆与入射杆接触、入射杆与岩石试样接触、岩石试样与透射杆接触，而岩石试样与节理层7e128e47da770e83e508ebcfb8ff1290361d9dc256b5461deae824261801177a的接触则使用CONTRACT_TIED_SURFACE_TO_SURFACE，此关键字用于模拟2个零件类似焊接、强力胶粘连，能极好地模拟岩石与节理面之间的关联。同时施加沙漏黏性阻尼力，其求解速度较快并能有效地保证结果的准确性。

3 数值模拟结果及分析

3.1 不同节理层厚度单层等间距的数值模拟结果及分析

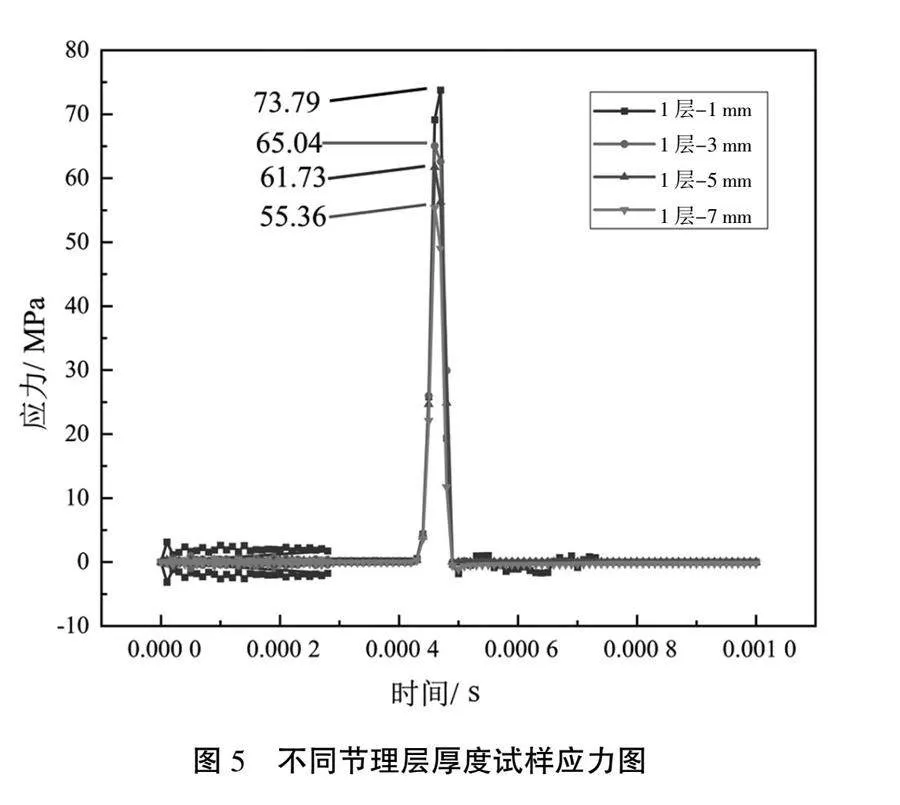
1、3、5、7 mm节理厚度的单层岩石试样的损伤云图如图4所示。峰值应力结果如图5所示。由图5可知，当节理层厚度为1、3、5、7 mm时，岩石试样的应力强度最大值分别为73.79、65.04、61.73、55.36 MPa，峰值应力随节理层厚度的增大而减小，节理层厚度为3 mm时，相较于节理层厚度为1 mm时，峰值应力强度下降了11.85%；节理厚度为5 mm时，相较于节理层为3 mm时，峰值应力强度下降了5.09%；节理层厚度为7 mm时，相较于节理层厚度为5 mm时，峰值应力强度下降了10.32%；节理层是岩体中的软弱层，当节理层的厚度越大，对岩石的削弱作用越强，所以当节理层的厚度越厚，岩石试样的峰值应力越小。

3.2 相同厚度不同节理层数等间距的数值模拟结果及分析

1 mm厚节理1、2、3、4层的岩石试样的损伤云图如图6所示。峰值应力结果如图7所示。由图7可知，当节理层数为1、2、3、4层时，岩石试样的应力强度最大值分别为73.79、64.77、58.64 、54.44 MPa，峰值应力随节理层数的增加而减小，节理层层数为2层时，相较于节理层层数为1层时，峰值应力强度下降了12.12%；节理层层数为3层时，相较于节理层层数为2层时，峰值应力强度下降了9.46%；节理层层数为4层时，相较于节理层层数为3层时，峰值应力强度下降了7.16%。相较于不同节理厚度的数值分析结果，节理层数的增加对岩石峰值强度的影响更大，造成这种影响主要是当应力波从试样传递至节理层时，由于试样与节理的力学特性不同，应力波在边界上发生反射与透射，当节理层数增多时，发生在试样上的透射与反射次数更多，对应力波的消耗越大。所以，节理层层数更多时，相较于同等厚度的单层节理，峰值应力更小。

4 结论

1）当节理的层数不变，节理层的厚度越大，岩体的峰值应力越小，节理层对岩体的削弱作用越强；

2）当节理层单层的厚度不变，节理层层数越多，岩体的峰值应力越小，节理层对岩体的削弱作用越强；

3）相较于节理层厚度的增加，节理层数量增多时，对于岩体峰值应力的影响更大。

参考文献：

[1] 李磊，谭忠盛，郭小龙，等．高地应力陡倾互层千枚岩地层隧道大变形研究[J].岩石力学与工程学报，2017（7）：1611-1622．

[2] 关宝树，赵勇．软弱围岩隧道施工技术[M].北京：人民交通出版社，2011．

[3] 米建宇，黄飞，李树清，等.基于SPH-FEM耦合算法的后混合磨料水射流冲击破岩数值模拟研究[J].振动与冲击，2021，40（16）：132-139.

[4] 席道瑛，陈林，张涛.砂岩的变形各向异性[J].岩石力学与工程学报，1995（1）：49-58.

[5] 高春玉，徐进，李忠洪，等.雪峰山隧道砂板岩各向异性力学特性的试验研究[J].岩土力学，2011，32（5）：1360-1364.

[6] 邓华锋，王伟，李建林，等.层状砂岩各向异性力学特性试验研究[J].岩石力学与工程学报，2018，37（1）：112-120.

[7] 陈新，廖志红，李德建.节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J].岩石力学与工程学报，2011，30（4）：781-789.

[8] 李海波，冯海鹏，刘博.不同剪切速率下岩石节理的强度特性研究[J].岩石力学与工程学报，2006（12）：2435-2440.

[9] 谢财进，饶军应，聂凯良，等.贵阳地区泥质白云岩电镜扫描试验及其损伤研究[J].施工技术，2018，47（S2）：1-7.

[10] 郝志斌，左宇军，刘镐，等.节理倾角对不规则砂岩破裂力学机制的影响研究[J].地下空间与工程学报，2022，18（6）：1906-1915.

[11] 卢玲，李启龙，徐志纯.三轴循环试验下节理板岩的力学特性研究[J].甘肃水利水电技术，2021，57（6）：57-60.

[12] 黄叶宁，邓华锋，李建林，等.水-岩作用下节理岩体剪切力学特性及本构模型[J].岩石力学与工程学报，2023，42（3）：545-557.

[13] 周文海，胡才智，包娟，等.含节理岩体爆破过程中应力波传播与裂纹扩展的数值研究[J].力学学报，2022，54（9）：2501-2512.