和直线与圆相关的文化创新问题解析

一、数形结合求最值

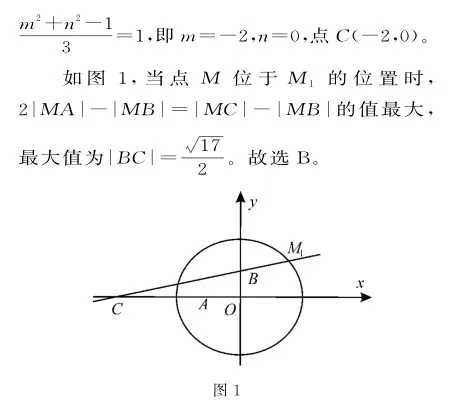
点评：本题主要考查直线和圆的位置关系。解决本题的关键是通过数形结合知两线段距离差的最值是在过点B、C的直线上。对于文化创新类的平面解析几何问题应特别注意数形结合思想的应用。

二、抓住对称性依托数形结合求最值

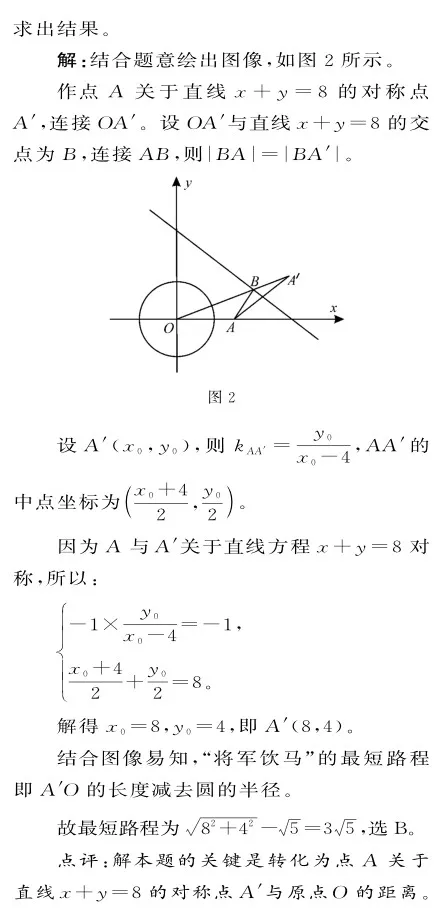
三、依托定义构造圆的方程确定直线的斜率

例3 古希腊数学家阿波罗尼斯的著作《圆锥曲线论》是古代光辉的科学成果，其中有这样一个命题：平面内与两个定点距离的比为常数k（ k>0， k≠1）的点的轨迹是圆，后人把这个圆称为阿波罗尼斯圆。已知定点A（ - 2， 0） ， B（ 2， 0） ，动点C满足| A C |= 2 | B C |，则动点C的轨迹为一个阿波罗尼斯圆，记此圆为圆P。已知点D在圆P上（点D在第一象限） ， A D交圆P于点E，连接E B并延长交圆P于点F，连接D F，当∠D F E= 3 0°时，直线A D的斜率为（ ）。

点评：本题的解答过程是先通过“阿波罗尼斯圆”的定义确定了圆的方程，再观察图像，利用题设条件，最终通过三角函数公式的运算求出直线的斜率。

（责任编辑 徐利杰）