高中数学拔尖创新人才培养课程体系建构与实施

摘 要 基于高中生数学核心素养的提升，以“教是为了不教”的育人理念为指导，构建“三阶”（巩固基础型课程、发展能力型课程、挑战荣誉型课程）“五维”（德育素养、文化素养、写作素养、建模素养、知识水平）的“三阶五维”高中数学拔尖创新人才培养课程体系，从培养对象、培养内容、培养方式三个方面展示“三阶五维”课程体系的实施路径，以期为当前中学及中学数学教师所面临的新挑战提供思路与对策。

关 键 词 拔尖创新人才；“三阶五维”课程体系；高中数学；数学核心素养；强基计划

引用格式 吴佐慧.高中数学拔尖创新人才培养课程体系建构与实施[J].教学与管理，2024（31）：16-19.

《国家中长期教育改革和发展规划纲要（2010-2020年）》指出，要“推进培养模式多样化，满足不同潜质学生的发展需要”，同时为了贯彻落实全国教育大会精神，服务国家重大战略需求，要加强加大拔尖创新人才的选拔培养。教育部在2020年1月印发了《关于在部分高校开展基础学科招生改革试点工作的意见》（以下简称《试点工作意见》），“突出基础学科的支撑引领作用”，标志着基础学科招生改革试点正式启动，迄今已遴选39所“双一流”高校作为试点，又称“强基计划”。强基计划强调探索多元录取机制，专门培养有志趣、有创新潜质的优秀青年成为我国人才储备军，以此推动综合评价改革，实现基础学科人才选拔和人才培养的有机结合[1]。

党的二十大报告中指出：“我们要坚持教育优先发展、科技自立自强、人才引领驱动，加快建设教育强国、科技强国、人才强国，坚持为党育人、为国育才，全面提高人才自主培养质量，着力造就拔尖创新人才，聚天下英才而用之。实施科教兴国战略，强化现代化建设人才支撑。”[2]高中阶段是学生个性形成、自主发展的关键时期，其中数学学科对学生综合思维能力的提升，尤其是促成学生拔尖创新更为重要。目前对数学拔尖创新人才的理解存在概念不清、内涵不明、标准单一的问题，社会更侧重于学生的数学学业成绩和数学学科竞赛成绩，对拔尖创新学生的发现与培养不足。需要明确的是“拔尖”并不一定“创新”，具有“创新”精神也可能在数学学习上不“拔尖”。

鉴于此，项目组成员以“教是为了不教”的育人理念为指导，于2010年开始持续开展了关于高中数学拔尖创新人才（资优生）培养的研究，经过在柳州高级中学多年的探索与实践，构建了“三阶五维”高中数学拔尖创新人才培养课程体系，探索了高中数学拔尖创新人才培养的新机制，为当前中学及中学数学教师所面临的新挑战提供了思路与对策。

一、“三阶五维”高中数学拔尖创新人才培养课程体系理论基础

在培养高中数学拔尖创新人才的过程中，学校构建了以教育心理学家约瑟夫·兰祖利的“三环模式”理论为核心的“三阶五维”人才培养课程体系。兰祖利的“三环模式”拓宽了对天赋学生的传统定义，打破了以往单纯依赖学术成绩或标准化测试评估学生的局限性。他认为，天赋不仅体现在高分上，更应该重视学生个体的差异性，尤其是那些具备独特创造力、非凡思维模式、创新表达方式以及强烈动机的学生，他们往往在传统教育评估体系中被忽视或低估[3]。兰祖利的“三环模式”理论强调三大要素——天赋行为、创意、投入，并认为学生的数学天赋与潜能不仅来源于智力水平，还需要具备高度的创造性和对学术、兴趣的深度投入。这一多维度的评估体系更好地识别了那些在传统教学中被忽视的非传统型优秀学生。通过包容与多元的视角，兰祖利的“三环模式”为教育者提供了一种新方法，让他们能够发现学生的潜在天赋，并提供更有针对性的高中数学拔尖人才课程体系，从而为学生的发展提供更多机会和更大空间[4]。

在此基础上，“三阶五维”课程体系深入融合了多种教育理论。首先，皮亚杰的认知发展理论强调学生的认知能力是通过主动建构知识实现的[5]，这与学校倡导的“教是为了不教”的理念高度契合。通过启发式教学，我们希望学生能主动参与知识的建构过程，而非被动接受知识，从而培养独立的思考能力与解决问题的能力。其次，建构主义教育理论强调学生在真实情境中通过协作、探究和反思来学习，这也为我们的课程体系提供了理论支持。通过在数学课堂中引入多维度的学习任务和开放性的数学问题，学生得以在实践中提升自己的创造力与逻辑思维能力。

结合上述教育理论，“三阶五维”课程体系通过多层级的数学课程设置以及多维度的评估方式、个性化的数学教学模式和创新型的数学学习环境，为数学拔尖人才提供个性化发展空间。学生不仅在学术上获得高成就，同时还能培养出独特的创造性思维和数学专业素养。我们的目标是通过这一模式，打破传统高中数学教学的局限，真正实现学生个体差异的尊重与人才的全面发展。通过对这些数学拔尖创新人才的培养，最终为数学学科的发展与创新注入新的活力。

这种理论体系的应用，不仅为当前的数学教育改革提供了新思路，也为推动数学拔尖人才的成长提供了坚实的理论基础和实践路径。在该体系的支持下，更多具备潜数学力但在传统模式下可能被忽略的学生，得到了更广泛的关注和培养，从而使他们能够充分发挥自己的天赋与才能，成为未来学术领域和社会中的佼佼者。

二、“三阶五维”高中数学拔尖创新人才培养课程体系建构

“三阶五维”高中数学拔尖创新人才培养课程是基于国家课程和柳州高级中学数学校本课程，对原有培养课程进行再次整合、补充和完善，构建充分满足学生个性化发展需求的数学课程体系，具有多样性、挑战性与跨学科性等三种特性，践行“教是为了不教”的教育理念，最终实现人的终身可持续的发展以及实现自我价值。

1.三阶

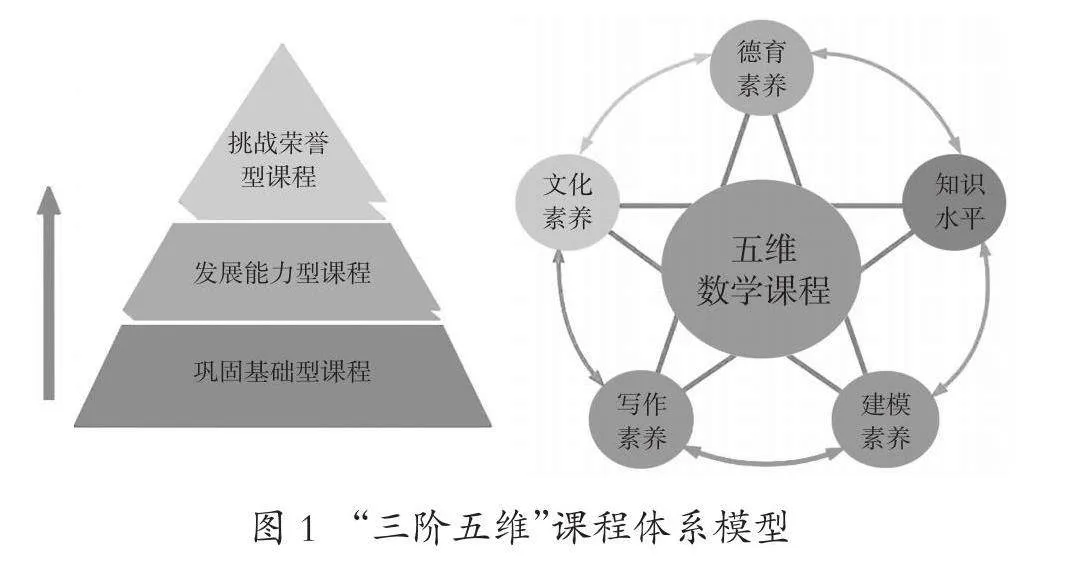
“三阶五维”高中数学拔尖创新人才培养课程体系中的“三阶”指巩固基础型课程、发展能力型课程和挑战荣誉型课程。首先，巩固基础型课程的主要目的是拓宽学生数学基础知识面，激发学生的数学学习志趣；教学内容涵盖国家必修课程和柳州高级中学数学校本课程，注重数学基础知识传授，渗透数学高阶思维，采用两个行政班合班管理模式，基本统一教学内容、进度和测评。比如数学竞赛的基础专题讲座、数学大学先修课讲座、高观点下的高中数学讲座、数学文化、数学写作、高校网络公开课、数学建模初步以及科技创新中的数学等。其次，发展能力型课程根据兰祖利“三环模式”引导学生对自己进行多维度的分析与测评，进行分专题的小班化教学以及导师制，选择适合自己的选择性必修课程；向数学拔尖创新人才提供国家选修课程和校本选修课程，采用独立班级的课堂教学，让拔尖创新人才在选择性学习的过程中，发现并初步坚定自己的数学志趣。最后，挑战荣誉型课程，适应特长发展需要，提升数学高阶思维能力，给拔尖创新人才提供个性化学习选择的机会，提升自我特长发展能力。比如：大学先修微积分、线性代数、强基数学、进阶数学建模、数学竞赛专题等[6-12]。

2.五维

“五维”是指拔尖创新人才培养数学课程涵盖的维度，包括以下五个方面：其一，德育素养。在学生培养过程中我们要时刻把握“育人先立德”，要引导学生形成正确的人生观、世界观、价值观，同时还要注意学生身心健康，且尽力提升学生的抗压能力和克服困难的毅力、决心以及团队合作能力以及学生的志向。其二，文化素养。对于数学拔尖创新人才培养我们不能只是对学生进行数学知识的讲授，也要注意文化素养的培育。数学家丘成桐先生认为：文化修养不仅能够培育人的意志，对科学研究也大有裨益。在学习数学的同时阅读一些数学家的传记，学习他们的精神，以及阅读与数学文化相关的书籍，对数学的理解也是有一定作用的。其三，写作素养。主要提升学生的文献检索、数学表达能力以及科研论文写作能力。其四，建模素养。通过数学建模的教学提升学生的模型意识，实现学科融合，进而“会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界”[13]。其五，知识水平。通过教师对学生“有限”知识的传授及思维能力培养，促使学生养成自学的习惯，提升学生分析问题以及解决问题的能力，最终实现“教是为了不教”（如图1）。

三、“三阶五维”高中数学拔尖创新人才培养课程体系的实施

经过对柳州高级中学多年教学实践的反思，笔者认为高中数学拔尖创新人才培养要从培养对象、培养内容以及培养方式三个方面着手。

1.培养对象：全体学生

最初学校对高中数学拔尖创新人才的认识具有一定的局限性，和大多数人一样，简单地认为数学竞赛成绩或高考成绩优秀的学生就是所谓的拔尖创新人才，也就是大部分人认为的“智优生”。但通过对皮亚杰儿童心理学发展理论、建构主义教育理论以及约瑟夫·兰祖利“三环模式”理论的学习以及研究，学校逐渐认识到高中数学拔尖创新人才培养对象应该是具有数学拔尖创新潜质的学生，是所有的学生。

创新是人的天性，任何学生都可能在某个方面具备创新的潜质。学生的能力素养是动态变化的，在学生成长的某些时期，不同的老师采用不同的培养方式教授不同的内容，也有可能会影响高中学生数学素养的提升，因此我们需要通过系统构建“三阶五维”高中数学拔尖创新人才培养课程体系，采用优秀的师资队伍对所有学生进行数学学习的启智培根以及差异化的培养，为他们的个性化发展打下坚实的数学基础。

2.培养内容：从高中数学学科知识到数学学科素养

第一，优化学校数学校本课程理念。根据不同层次的学生制定不同的数学课程目标，同时进一步优化校本数学课程结构，丰富完善校本数学课程，整合数学课程内容，加强校本数学课程的管理与实施，构建指向高中数学核心素养提升动态的“三阶五维”课程体系，并通过项目式以及探究式等课程形式促进学生数学高阶思维以及学习力的提升。

高中数学教学活动中知识的传授并非仅仅局限于“教”与“学”的单向流程，而是基于深思熟虑的课程设置和独具匠心的教学模式悄然实现知识的传递与深化。因此，需要数学教师不断优化自己的教学内容，整合高中数学拔尖创新人才培养的教学资源，确保数学课程安排具有弹性。在汲取丰富的高中数学课程改革经验的基础上，教师致力于对课程设置方案进行更为精细的完善，强化高中数学各个学习阶段中数学学科课程内容的有效链接，加深学校提供的数学课程与数学拔尖创新学生的互适性。

第二，通过相应的数学课程提升高中数学拔尖创新学生的数学知识积累能力以及数学素养五个维度的课程：德育素养、文化素养、写作素养、建模素养、知识水平。例如初高中衔接课程、德育课程、数学文化、国家必修课程、国家选修课程、校本选修课程、数学竞赛初步、强基课程、数学竞赛拓展、数学写作、大学先修课程以及数学建模课程等系列课程群，通过科学系统而深入的课程学习，让学生的数学知识体系更加完善，基础更加扎实，在强化学生数学基础的前提下，增加数学课程的深度与宽度。

学生进入高中以后，在三年的数学学习过程中，我校充分尊重学生数学学习个体需求，根据学生自己的志趣，结合大数据精准靶向教学以及不同阶段的心理测评，让学生能够更加清晰地认识自我，不断激发自己数学学习的内驱力。

第三，培养学生的问题意识、批判性思维以及创新能力。丘成桐先生认为：一流人才，始自学“问”，最主要的是提出问题，我们要培养现在的年轻人，帮助他们提高找出重要问题的能力。我校通过高中数学拔尖创新人才培养“三阶五维”课程的设置，引导学生独立思考、提出问题，进而进行对比和批判性思考，打破常规数学思维的藩篱，发展学生的数学创新性思维。

第四，在真实情境问题的引领下，培养学生跨学科的综合能力，促进学科间的深度融合。这一举措不仅是对传统数学单科教育的有力补充，更是为了进一步激发学生的创新思维，提升他们解决实际问题的能力。通过数学建模、科技创新以及STEM教育等多元化的教学手段，鼓励学生将理论知识与实践相结合，培养他们的综合素质和创新能力。

3.培养方式：双导师制下的小班化与动态调整的高中数学拔尖创新人才培养

（1）结合大数据精准靶向数学教学，确定各层次各类型课程的选修学生

基于学生个人情况，遵循自愿进出、双向选择的原则，实施小班化教学，并构建高中数学拔尖创新人才培养的动态调整机制。通过面试、“即学即考”的笔试、日常数学课堂的细致观察，结合平时数学成绩、强基数学实力、数学竞赛表现、大学选修课程掌握情况、数学建模能力等多维度指标的综合测评，将对不适应此类课程的学生进行妥善分流。同时，若其他类型班级中有学生展现出对此类课程的适应性，在其个人意愿的基础上，我校将予以补充，以实现学生的差异化培养，并为每位学生量身定制个性化的培养方案。

（2）试行双导师制度，即学术导师与项目导师协同合作模式

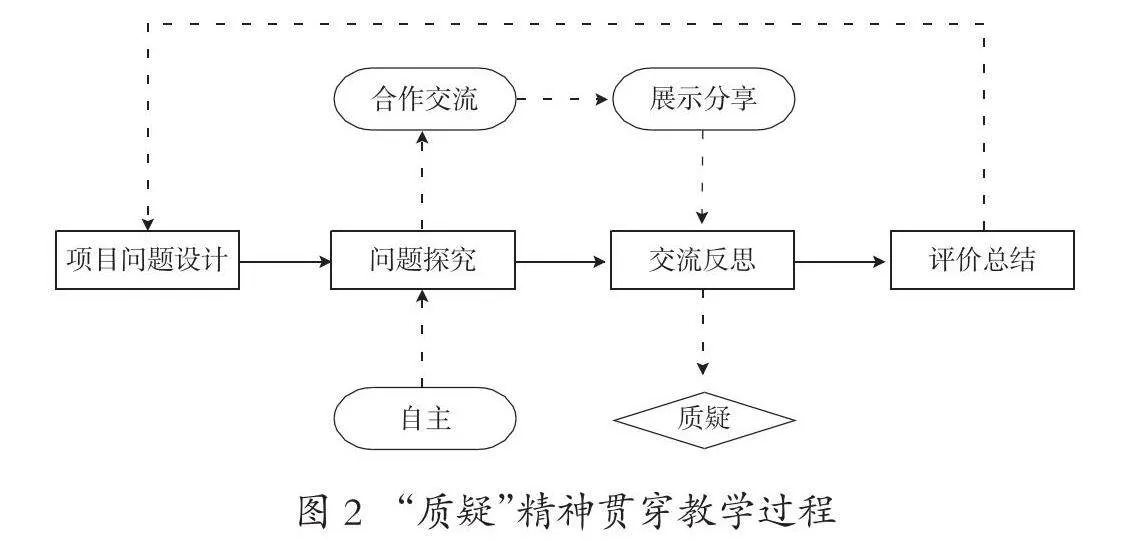
学术导师专注于高考、强基计划、数学竞赛以及大学先修课等学术领域的指导，而项目导师则主要负责数学建模、科技创新以及STEM教育等实践项目的引导。此外，项目导师还将担任学习小组或学习共同体的指导教师，以确保学生的实践活动得以高效推进。无论是学术课程还是项目式课程，我校都秉持“自主、合作、分享、交流反思”的教学理念，并将“质疑”的精神贯穿于整个教学过程之中，以激发学生的求知欲和创新精神（如图2）。

综上所述，高中数学拔尖创新人才培养是一个系统工程，需要各方面的共同努力。同时“三阶五维”高中数学拔尖创新人才培养课程体系的构建以及实践也需要学校和教师的共同配合与努力。一方面，学校层面需要多维度的整合优势高中数学教学资源，为其实施提供基础的物质以及制度保障，比如有相应的资金以及完善相关的激励政策等支持教师编写数学拔尖创新人才培养校本教材讲义等。另一方面，学校努力打造一支高素质数学拔尖创新人才培养的师资队伍，增加能胜任“三阶五维”高中数学拔尖创新人才培养的师资数量，强化师资培训质量，有效调动数学教师的主动性以及自觉性，同时采取“引进来、走出去”的方式，为教师们提供共享优质资源，拓展他们的视野，努力更新他们的教育理念。希望通过“三阶五维”高中数学拔尖创新人才培养课程体系的构建以及高中数学拔尖创新人才培养的新机制的探索，在师生的共同努力下，经过高中三年的培养与提升都能够做到数学根基牢固，素养厚实，不同类型的师生都能得到相应的发展与提升。

参考文献

[1]教育部等六部门关于实施基础学科拔尖学生培养计划2.0的意见：教高〔2018〕8号[A/OL].（2018-10-08）[2023-10-11].http：//w

ww.moe.gov.cn/srcsite/A08/s7056/201810/t20181017_351895.html.

[2] 习近平. 高举中国特色社会主义伟大旗帜为全面建设社会主义现代化国家而团结奋斗： 在中国共产党第二十次全国代表大会上的报告[EB/OL].（2022-11-01）[2023-10-11].http：//www.qstheory.cn/dukan/qs/2022-11/01/c_ 1129089160.htm.

[3][4] 兰祖利，里斯. 丰富教学模式：一本关于优质教育的指导书[M].华华，译.上海：华东师范大学出版社，2000：1，1.

[5] 沃兹沃思.皮亚杰认知和情感发展理论[M].5版.杨砚秋，译.上海：华东师范大学出版社，2022：11.

[6] 吴佐慧.高中数学建模校本课程体系的构建与实践[J]. 数学通讯，2022（02）：36-38+40.

[7] 吴佐慧，叶瀚文. 基于学术志趣的高中数学建模教学实践研究[J]. 数学通讯，2021（02）：27-30+54.

[8] 吴佐慧，曾露仪.高中数学建模教学关键问题的探索与解决思路[J].广西教育，2021（06）：60-63.

[9] 吴佐慧，曾露仪.拔尖创新人才培养视域下数学建模的教学设计与思考[J]. 数学通讯，2023（23）：14-17.

[10] 吴佐慧，彭培盛.中国大学先修课程（CAP）微积分的实践研究——以柳州高级中学的教学实践为例[J]. 数学教学，2019（11）：14-16+50.

[11] 吴佐慧.射影几何在高中圆锥曲线问题中的应用[J]. 数学通讯，2020（14）：41-43+46.

[12] 吴佐慧，叶瀚文.HPM视角下的基本不等式教学[J]. 数学通报，2020（06）：37-42.

[13] 史宁中，王尚志.普通高中数学课程标准（2017年版）解读[M]. 北京：高等教育出版社，2018：5.

【责任编辑 王泽华】