基于Matlab线性规划二次优化在钢筋下料中的应用

摘要：以西渝高铁某钢筋加工厂钢筋下料为背景，提出一种通过两次优化过程，建立方案组合筛选和方案组合一维线性规划模型，使得复杂的优化数学理论问题变得直观易懂。该方法通过算例，利用计算机辅助计算软件Matlab，将上述数学模型应用于施工现场，提高钢筋下料计算效率和自动化程度，提升了材料的利用率，从而达到节约成本的目的，具有很强的实用性。

关键词：一维线性规划二次优化Matlab软件成本控制

中图分类号：O221.1;TU755.3

ApplicationofLinearProgrammingQuadraticOptimizationBasedonMATLAB

inRebarCutting

ZHANGZhongliang

The4thEngineeringCo.，Ltd.，ofChinaRailway20thBureauGroupCo.， Ltd.，QingdaoCity，ShandongProvince，266061China

Abstract：Inthispaper，basedontherebarcuttingprocessinareinforcingbarprocessingplantofXi’an-Chongqing（Xiyu）high-speedrailway，aquadraticoptimizationprocessisproposedtoestablishthemodelofschemecombinationscreeningandone-dimensionallinearprogrammingofschemecombination，makesthecomplexoptimizationofmathematicaltheoryproblems becomeintuitiveandeasytounderstand.Themethodappliestheabovemathematicalmodeltotheconstructionsitebymeansofanexampleandthecomputer-aidedcalculationsoftwareMATLAB，whichimprovesthecalculationefficiencyandautomationdegreeofrebarcuttingandtheutilizationratioofmaterials，achievingthepurposeofcost-saving，whichstrongpracticality.

KeyWords：One-dimensionallinearprogramming;Quadraticoptimization;Matlabsoftware;Costcontrol

西渝高铁作为我国重要的在建高铁项目，在我国的交通运输中发挥着重要作用。钢材作为铁路建设中的重要物资，在成本控制中占据重要的地位。以某标段为例，正线长度30km，钢材使用量为10.2万t，其中钢筋为4.19万t，占比95.2%。钢筋下料是钢筋加工的重要环节，通常钢筋下料人工凭经验完成，不仅耗时，钢筋利用率不高，使得企业的经济效益降低。钢筋优化下料就是通过对大量待加工钢筋进行筛选比较、优化组合，达到更多地节省钢筋原材料的目的，其优化目标值是使用的钢筋原料最少。钢筋优化下料问题是个典型的一维优化组合问题。对于小规模下料，通过方案组合筛选，线性规划的方式在施工现场钢筋下料中具有很好适用性。

1需求分析及数学模型

长度常为12m或9m，此种钢筋常作为主筋使用，下料长度不定，最短的长度常在0.8m以上，也就是说0.8m以下的钢材有可能作为余料丢弃，以余料为0.8m为例，钢筋利用率为（9-0.8）/9=91.11％，存在巨大的改进空间。因此通过钢筋的优化组合使钢筋的利用率提高主要是针对定长钢筋，也即是本文要讨论的对象。

本文讨论的对象忽略切口影响。需求的定义示例如下：设单根的定长钢筋长度为L，在此中钢筋上裁剪长度分别为a1、a2、a3的半成品，一根线材上所下的3种半成品的数量为x1、x2，x3，分割的公式可表示为

a1x1+a2x2+a3x3≤L

半成品的切割方式向量为x（x1，x2，x3），半成品向量为l（x1，x2，x3），即在长度为L的钢筋上切割x1个a1，x2个a2，x3个a3个。由于订单要求的半成品的长度有多种可能的组合，下料的方式也可能有好多种。

决策变量：用xj表示按照第j种切割方式所使用的钢筋根数，明显xj是非负的整数，用xij表示按照第j种切割方式，一根线材所切割下来的第j种需求坯料的数量。

其中矩阵A，矩阵X代表每一种分割方案对应采用的数目，矩阵b不等式约束的资源数。

2数学模型求解

2.1计算步骤

Step1：导入下料长度表，包含半成品种类、长度、数量，能够接受的余料的长度[3]。

Step2：求解单根原材生产对应生产的某种半成品最大值。

Step3：枚举法计算列出不同的下料方案，根据方案筛选器和余料调节器，筛选出方案余料的接受值，并选择满足条件的所有的方案组合。

Step4：方案矩阵转置，列出目标函数及约束条件，转换成Matlab可以接受的基本型。

Step5：利用软件根据约束条件，目标函数计算每种下料方案的循环次数及方案组合。

Step6：输出下料长表（包含方案循环次数、下料长度、数量、材料利用率、余料长度等）。

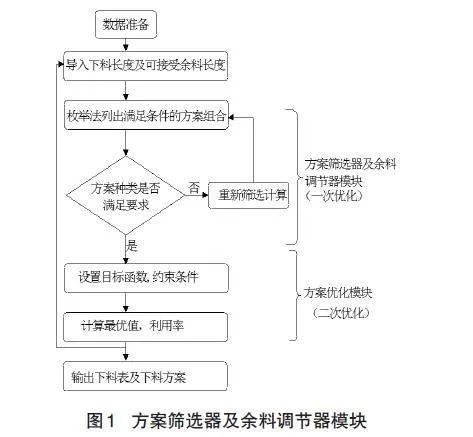
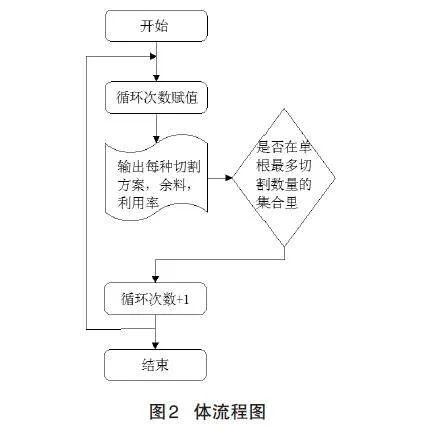
2.2评价指标及流程图

生产中常用的评价指标为钢筋的利用率，其公式[3]为：

• 编程实现及算例

本文采用φ22的螺纹钢为例，首先进行方案筛选及余料调节，原材料长度为L=9000mm。

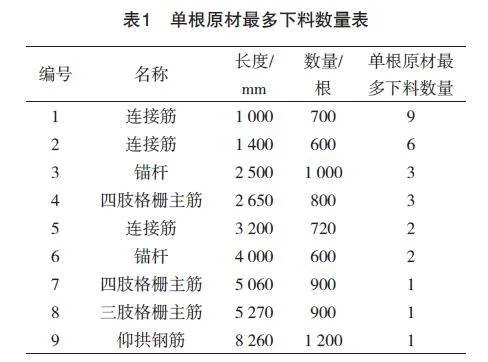
首先按照钢筋长度进行排序，以下料长度为计算对象，计算单根原材最多下料数量，如表1所示[5]。

以上述表中的单根原材最多下料数量作为方案的迭代次数的运行条件，程序实现如下：

i=0;

forx1=0：9

forx2=0：6...........forx9=0：1

r=9-x1*x1+1.4*x2+2.5*x3+2.65*x4+3.2*x5+4*x6+5.06*x7+5.27*x8+8.26*x9）;

if（r>=0）&&amp;（r<1）

if（r<0.1）%余料长度调节器

number=number+1;

fprintf（'%3d%3d%3d%3d%3d%3d%3d%3d%3d%3d%3d%3d＼n'，number，x1，x2，x3，x4，x5，x6，x7，x8，x9，r，（9-r）/9*100）;

............

end

end

上述过程中当余料长度调节器分别设定0.74、0.5、0.3、0.2、0.1时所有的组合数量分别为57、39、26、24、15；最大的一种材料长度为8.26m，只能生产一种，余料为0.74m；其他方案产生的余料长度不是最优化的长度。故此时包含了第一次的优化筛选，本筛选满足的条件有两个：第一，保证余料为设定的理想值[4]；第二，保证方案选项中包含生产所有的半成品料。本例中设定的余料接受值为0.1m，而此时没有包含生产8.26m的方案，故在最后的条件中加入，这样就能满足上述两个条件。由上得出第一次优化筛选小于0.1m的方案组合的矩阵。

将上述方案得出矩阵进行转置，并将目标函数及约束条件转化成标准型，带入程序实现。

程序如下：

clc，clear;

f=[1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1];%目标函数

A=[*******************];%方案矩阵

b=[-700，-600，-1000，-800，-720，-600，-900，-900，-1200];%b

lb=zeros（16，1）;

intcon=[1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16];

[x，fval]=intlinprog（f，intcon，A，b，[]，[]，lb，[]）;%整数型线性规划

x，fval=fval

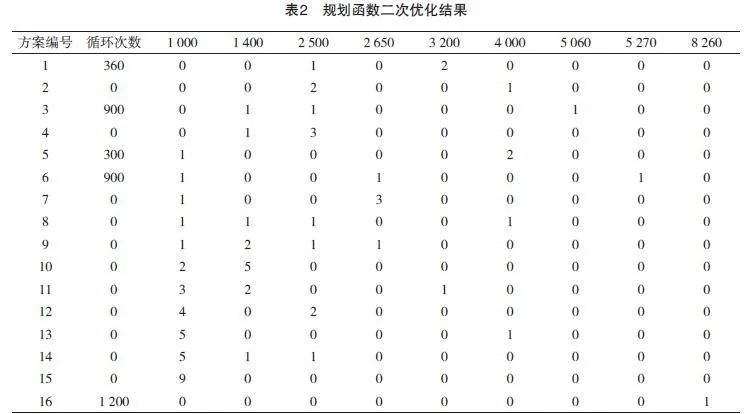
至此通过规划函数进行了第二次优化。计算结果如表2所示。

通过优化得出如下结果：方案1加工次数：360次，余料长度360×0.1m，利用率98.9%；方案3加工次数为：900次余料长度为900根×0.04m，利用率：99.6％；方案5加工次数为：300次余料长度为0，利用率：100％；方案6加工次数：900次，余料长度900根×0.08m，利用率：99.6％；方案16加工次数：1200次，余料长度1200根×0.74m，利用率：91.77％.目标函数原材利用数量为3660根，综合利用率为：（360×98.9%+900×99.6％+300×100％+900×99.6％+1200×91.77％）/3660=96.99％.最后一种余料长度为0.74m，可以进入下一批次的优化，以取得更好的材料利用率。

4结语

本文通过在对本标段钢构厂进行实践，取得了良好的效果，建立的一维下料的数学模型，利用Matlab进行数据处理，通过一次余料优化，筛选余料最少的方案组合。二次优化通过利用整型规划函数进行优化，得出方案最佳组合，从而给定本批次的局部的下料组合。使得钢筋原材数量最少，有效地导钢筋下料，达到节约成本的目的，取得了良好的经济效益，具有很强的可推广性。

参考文献

[1]马浩.F型钢一维下料的优化算法[J].山西建筑，2023，49（23）：149-150.

[2]田飞，符学勇.基于线性规划模型钢材下料问题最优切割方案研究[J].科学技术创新，2023，（23）：194-198.

[3]钱辉.建筑工程钢筋下料优化分析方法及软件开发[D].南昌：南昌大学，2023.

[4]王朝晖，曹阳.整数规划近似算法在钢筋下料中的应用研究[C]//中国建设科技集团股份有限公司，中国建筑学会工程总承包专业委员会，中国中建设计集团有限公司等.第二届工程总承包项目管理经验交流会暨2019中国建筑学会工程总承包专业委员会年会论文集.中国建筑第五工程局有限公司，2019：5.

[5]万书霞.某项目钢筋工程数字化及下料优化研究[D].邯郸：河北工程大学，2021.