整车质心位置测量与不确定度评定

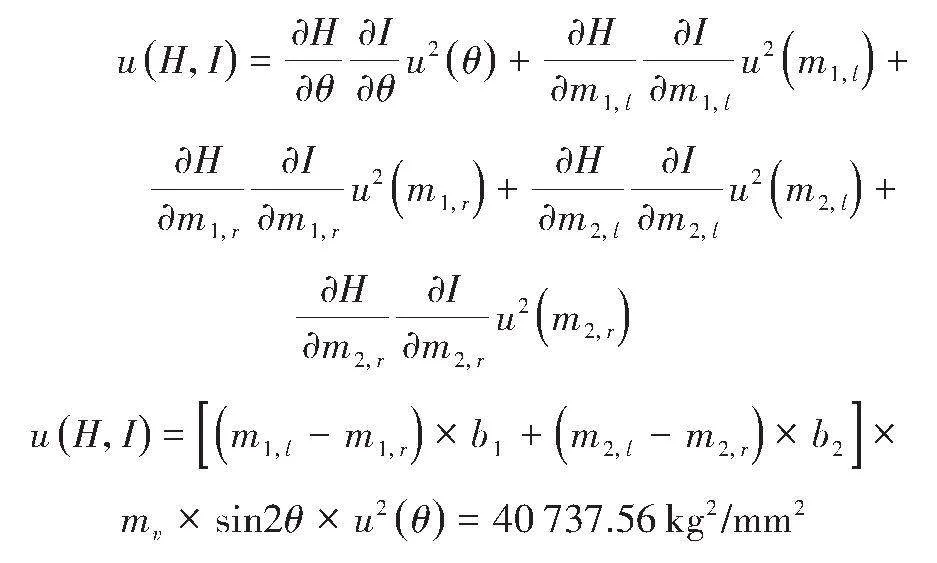
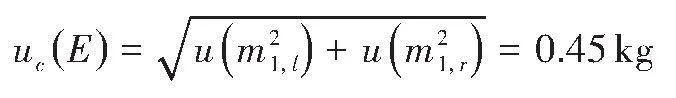
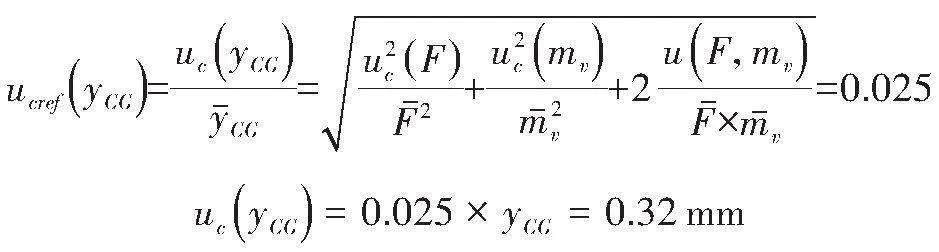
摘要：整车质心位置是影响汽车安全行驶的重要参数之一。准确测定车辆质心位置以及在测量过程中进行不确定度的评定，可以更准确地预测和评估车辆的动力性，提高车辆的安全性和操纵稳定性。据此，在实验室具备侧倾试验台的情况下，采用侧倾试验台法在空载状态下进行了整车质心横向位置、纵向位置、高度3个参数的测量，同时进行了不确定度的评定。

关键词：安全行驶；侧倾试验台法；质心横向位置；纵向位置；高度；不确定度

中图分类号：U467.1+2 收稿日期：2024-06-20

DOI：10.19999/j.cnki.1004-0226.2024.09.020

1 前言

随着汽车工业的飞速发展，车辆的行驶安全性越来越受到人们的关注。在车辆性能参数中，整车质心高度是一个重要指标。车辆重心高度对操纵稳定性、行驶平顺性、驾乘舒适性等有着重要影响，例如在加速、制动、转向时车辆重心发生转移，车身的姿态、悬架状态、转向特性都会受到影响，尤其是急加减速、高速过弯时。重心转移量取决于重心高低。重心越低，则重心转移越小，操纵稳定性、行驶平顺性、驾乘舒适性等性能也更好。但受制于成本、技术等各种因素，重心高度不可能很低。鉴于重心高度对车辆各种性能的重要影响，精确测量其值并确定其不确定度显得十分必要[1]。

GB/T 12538—2023《道路车辆质心位置的测定》代替了GB/T 12538—2003《两轴道路车辆重心位置的测定》，新标对汽车重心高度测定采用的是抬高轴法、稳定摆法与侧倾试验台法，抬高轴法与稳定摆法在实际操作起来不方便。试验室在具备汽车侧翻台设备的基础上，根据文献[2]与文献[3]的要求，检测实验室在采用新的检测方法时，应按照新方法重新评估测量不确定度。

本文依据JJF 1059—2012《测量不确定度评定与表示》对在车辆重心高度测定过程中所产生的不确定度进行全面的评估。

2 试验原理

侧倾试验台法的原理是利用质量反应法计算质心高，侧倾试验台法的质量转移发生在左右两侧。根据力矩平衡原理，测量车辆两侧的轮荷、总质量、轮距、水平质心位置及侧倾角度，通过公式计算出质心高（zCG）。在此方法中，假定车辆为刚体，但在实际测量过程中，车辆本身是一个弹性系统，侧倾时由于受悬架、轮胎的弹性变形，油、水等液体的流动，零部件之间的间隙变化等因素的影响，车辆质心相对于车辆有所变化。因此在测量时，要采取一定措施以最大限度降低此类影响。测量时，装载载荷要固定可靠，以避免由于车辆倾斜而引起的位移。轮荷和侧倾角度的测量精度直接影响最终的测试精度，因此尽可能采用测量精度较高的侧倾试验台。测量时的侧倾角度对结果有直接影响：角度太小，质量转移不明显，测量准确度不高;角度太大，质量转移较大，轮胎的变形影响测量结果。因此侧倾角度不能太大也不能太小[4]。

3 建立数学模型

3.1 质心纵向位置

质心纵向位置公式如下[4]：

式中，[xCG]为车辆质心距第一轴中心线的水平距离，为质心纵向位置，mm；[mi，l]为第i轴左轮荷，kg；[mi，r]为第i轴右轮荷，kg；[l1i]为车辆第一轴至第i轴轴距，mm；[mv]为整车质量，kg。[mv]的计算公式如下：

3.2 质心横向位置

质心横向位置公式如下[4]：

式中，[yCG]为车辆质心与车辆纵向中心面之间的水平距离，即为质心横向位置，mm；[bi]为第i轴轮距，mm。

3.3 质心高度

3.3.1 车辆左倾质心高度计算公式

车辆左倾质心高度计算公式如下[4]：

式中，[zCG，l]为车辆左倾时质心高度，mm；[mil，θ]为倾斜角度为θ时，车辆第i轴左侧车轮的轮荷（垂直于支撑面方向），kg；[mir，θ]为倾斜角度为θ时，车辆第i轴右侧车轮的轮荷（垂直于支撑面方向），kg；θ为侧翻试验台倾斜角度，（°）。

3.3.2 车辆右倾质心高度计算公式

车辆右倾质心高度计算公式如下[4]：

式中，[zCG，r]为车辆右倾时质心高度，mm。

车辆的质心高（[zCG]）为式（4）与式（5）的算术平均值，即[zCG=zCG，l+zCG，r/2]。

3.4 常用合成标准不确定度计算公式[5]

3.4.1 线性模型合成标准不确定度评定

具体公式形如：

[Y=A1X1+A2X2+L+AnXn] （6）

①当各变量不相关时，则合成标准不确定度计算公式为：

②当各变量相关时，则合成标准不确定度计算公式为：

3.4.2 非线性模型合成标准不确定度评定

具体公式如下：

[Y=AXp11Xp22LXpnN] （9）

①当各变量不相关时，则相对合成标准不确定度计算公式为：

②当各变量相关时，则相对合成标准不确定度计算公式为：

4 质心位置不确定度的计算与评定

4.1 质心纵向位置扩展不确定度评定

由式（1）可知，对质心纵向位置产生影响的分量有整车整备质量、后轴载质量、车辆轴距，采用A类不确定度进行重复性评定；车辆状态、悬架状态、车辆停放位置、汽油油量等误差采用A类不确定度进行评定；测量设备精度、人员读数误差等引入的不确定度采用B类不确定度进行评定。某款被测车型左侧轴距（l12，l）、右侧轴距（l12，r）、各轴轴载质量（m1，l、m1，r、m2，l、m2，r）、轮距（b1、b2）以及根据式（1）与式（3）计算的xCG，yCG参数见表1。表1中各参数A类重复性不确定度均采用贝塞尔公式进行不确定度评定。贝塞尔公式如下[5]：

由此可计算出各参数的A类重复性不确定度：

下面进行质量测量。由侧翻台引入的不确定度按照B类不确定度方法进行评定。由校准证书可知，其称重台单块板扩展不确定度U=1 kg，k=2；单块测量平台引入的B类不确定度为uB（单个称重台）=U / k =0.5 kg。检定侧翻试验台的砝码质量误差等级为M1等级，M1等级砝码的允许误差在±0.005％之内，该影响因子较小，可不予考虑。

由此可计算出各分量的合成标准不确定度分别为：

由不确定度传播率得：

记后轴轴载质量为D，即D = m2，l + m2，r；质心纵向位置计算模型为[xcg=D×l12/mv]。

后轴轴载质量D的合成标准不确定度为：

整车整备质量mv的合成标准不确定度为：

D与mv相关，相关参数为[m2，r]与[m2，r]，D与mv的协方差u（D，mv）为：

质心纵向位置的相对合成标准不确定度为：

因此，质心纵向位置的合成标准不确定度为uc（xCG）=ucref （xCG）×xCG=1.64 mm；取包含因子为k=2，其扩展不确定度为U=k×uc（xCG）=3.28 mm。

4.2 重心横向位置扩展不确定度评定

选用两轴车辆进行测量，重心横向位置测量模型为：

令前轴轴荷差为E，后轴轴荷差为F，即：[E=m1，l-m1，r]，[F=m2，l-m2，r]。令G = Eb1 + Fb2，则CG = G / 2mv，根据不确定度传播理论，F与mv相关，相关参数为m1，l与m1，r、m2，l、m2，r。

E的合成标准不确定度uc（E）：

同理，F的合成标准不确定度uc（F）为：

G的合成标准不确定度uc（G）为：

G与mv的协方差u（G，mv）为：

则yCG的相对合成标准不确定度ucref （yCG）为：

取包含因子k = 2，其扩展不确定度U为：

U = k × uc （ yCG ） = 0.64 mm

4.3 车辆左侧翻转质心高度合成标准不确定度评定

左侧翻转质心高度计算公式：

用角度仪测量侧翻台角度翻转7°、8°、9°、10°、11°共5个角度值，分别测定侧翻台角度引入的不确定度分量，结果如表2所示。

由于测量次数相对较少，采用极差法[5]进行侧翻台翻转角度与车辆垂直载荷进行A类不确定度评定，即：

式中，R为极差，为测量值中最大值与最小值之差；C为极差系数，由表3确定；n为测量次数。

当角度为7°时，侧翻台重复性引入的角度与垂直载荷的不确定度为：[uA7°=0.017°]，[uAm1l，7°=0.68 kg]，[uAm1r，7°=0.34 kg]，[uAm2l，7°=0.34 kg]，[uAm2r，7°=0.34 kg]。

角度仪测量侧翻台角度引入的不确定度按照B类方法进行评定，角度仪误差为±0.1°，假设为均匀分布，k=

侧翻台角度值引入的不确定度按照B类方法度进行评定，由侧翻台校准证书可知，角度不确定度U=0.05°，k=2，因此侧翻台引入的不确定度分量为uBθ（侧翻台）=0.05°/2=0.025°。

由此可得到各参数的合成标准不确定度：[uc7°=0.065°，ucm1l，7°=0.84 kg，ucm1r，7°=0.60 kg，ucm2l，7°=0.60 kg，ucm2r，7°=0.60 kg]。

同理计算出其余各角度下各参数的合成标准不确定度。

当翻转角度为7°时，将质心高度测量模型展开可得到：

则可将原式化为积商形式：zCG = H / I 。由于sinθ与cosθ是明显非线性函数，可根据泰勒级数展开为线性表达式。忽略其高阶项，由于uc（θ）=0.065°，可得sinθ与cosθ的不确定度：

由G等式可得其合成标准不确定度：

令J=（（[m1l，θ-m1r，θ]）-Ecosθ）b1=127 330.38 kg/mm，则其合成标准不确定度为：

uc（J）=0.013×127 330.38 kg·mm=1 688.31 kg·mm

同理，令：

K=［（m2l，θ-m2r，θ）-Fcosθ］b2=91 487.44 kg/mm

uc（K）=0.018×91 487.44 kg·mm=1 374.39 kg·mm

J与K相关，相关参数为cosθ，J与K的协方差为：

H等式合成标准不确定度为：

由等式I可得：

H与I相关，相关参数为θ、m1，l、m2，l、m1，r、m2，r，其协方差为：

由此质心高度计算公式为zCG，l =H/I，其合成标准不确定度为：

根据上述方法，可计算出个角度下质心高度的合成标准不确定度。

左侧翻转的质心高度为其5次计算出质心高的平均值，因此，uc（zCG，l）=10.69 mm。

4.4 车辆右侧翻转质心高度合成标准不确定度评定

右侧翻转质心高度计算采用与左侧翻转质心高度不确定度评定同样的计算方法，用角度仪测量侧翻台角度翻转7°、8°、9°、10°、11°5个角度值，分别测定侧翻台角度引入的不确定度分量，结果如表4所示。

根据表4，可得右侧翻转时质心高度的合成标准不确定度为uc（zCG，l）=10.69 mm。

4.5 车辆右侧翻转质心高度扩展不确定度评定

整车质心高为左侧翻转质心高度计算值与右侧翻转质心高度计算值的算术平均值，则zCG =698.37 mm。

根据不确定度传播率得，整车质心高度的不确定度为uc（zCG）=7.52 mm。取包含因子k=2，其扩展不确定度为U=15.04 mm。

5 结语

在被测某款车型空载状态下进行质心测量，影响质心位置的不确定度影响因子为卷尺精度、侧翻台质量测量与角度测量精度、人员读数误差、车辆状态等。考虑被测量所有误差后整体计算得出整车质心纵向位置扩展不确定度U95（xCG）=3.28 mm、整车质心横向位置扩展不确定度U95（yCG）=0.64 mm，以及整车质心高度的扩展不确定度U95（zCG）=15.04 mm。

参考文献：

[1]李涛，卢海波，林泛业，等.Analysis of the Measurement Errors of CG Height[C]//2018中国汽车工程学会年会论文集.北京：中国汽车工程学会，2018：3.

[2]CNAS—CL01：2018 检测和校准实验室能力认可准则[S].

[3]CNAS—CL01—G003：2021 测量不确定度的要求[S].

[4]GB/T 12538—2023 道路车辆质心位置的测定[S].

[5]JJF 1059.1—2012 测量不确定度评定与表示[S].