基于Hansbo渗流的平面应变固结分析


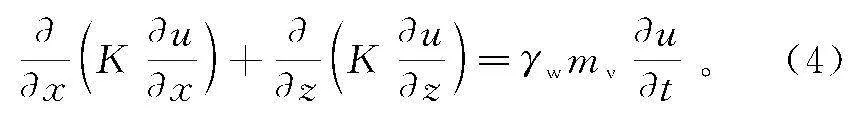
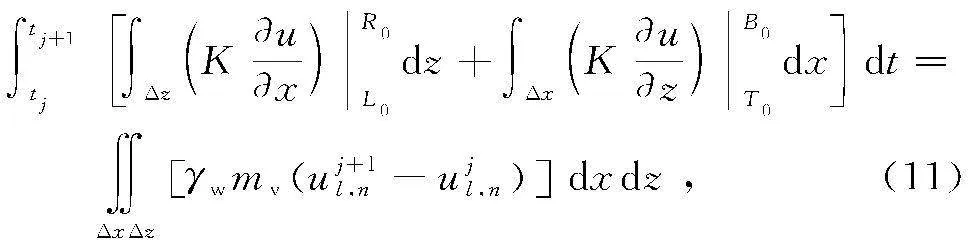

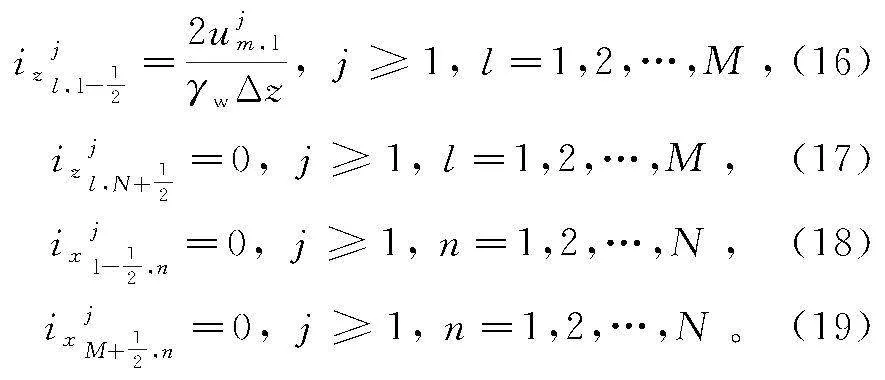
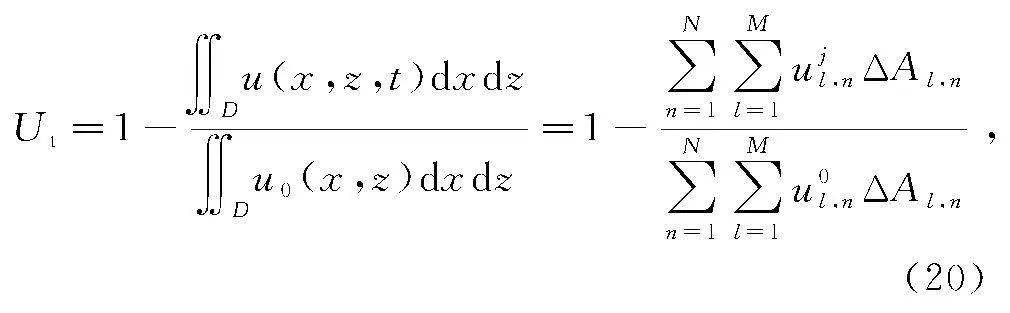
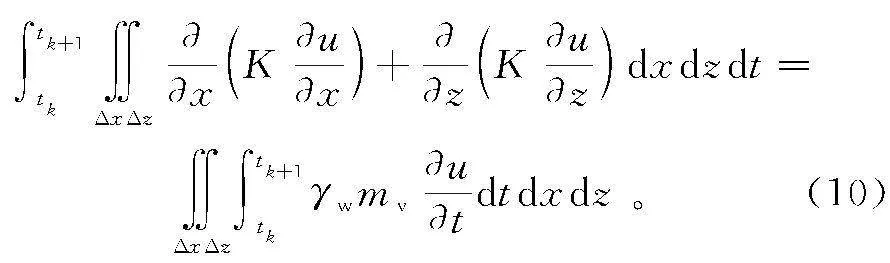
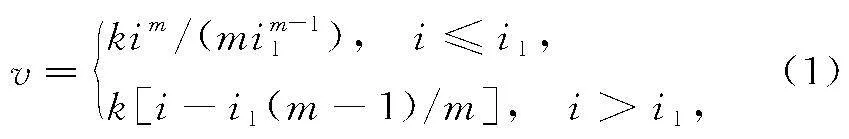
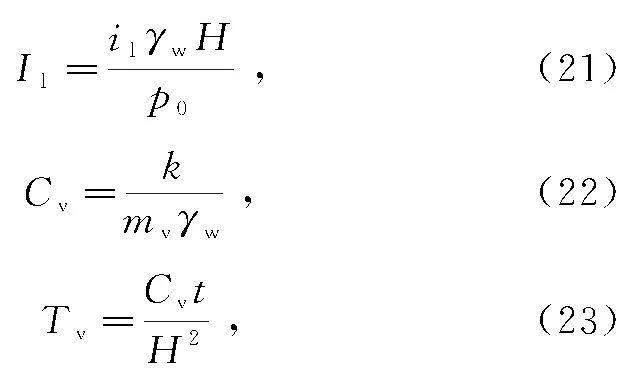

摘 要:为了考察非Darcy渗流对二维地基固结过程的影响,引入Hansbo渗流方程描述饱和黏性土中的渗流规律,修正了Terzaghi-Rendulic平面应变固结方程,并给出了有限体积法数值求解格式;采用不同的Hansbo渗流参数,分析了条形荷载作用下有限深度地基的固结特性。结果表明:Hansbo渗流延缓了平面应变固结的过程,并且随着Hansbo渗流参数的增大,超静孔压的消散变得更为缓慢,因此,按Darcy渗流对二维地基进行的常规固结分析将会高估其固结速率;与Biot固结理论相比,在Terzaghi固结理论框架内,条形荷载下固结初期地基中局部的孔压增大现象并不明显。研究成果可为探寻更为准确的饱和黏性土地基沉降预测方法提供理论基础。
关键词:地基基础工程;平面应变固结;饱和黏性土;Hansbo渗流;有限体积法
中图分类号:TU432 文献标识码:A
Analysis of plane-strain consolidation based on Hansbo′s flow
Abstract:
In order to investigate the influence of non-Darcian flow on the consolidation process of two-dimensional soil layer, Hansbo′s flow equation was introduced to describe the flow law in saturated cohesive soil, the Terzaghi-Rendulic plane strain consolidation equation was modified, and the finite volume method numerical solution scheme was given. The consolidation characteristics of finite depth foundation under strip load were analyzed by using different Hansbo′s flow parameters. The results show that Hansbo′s flow retards the plane strain consolidation process, and the excess pore pressure dissipates more slowly with the increase of Hansbo′s flow parameters. Therefore, the conventional consolidation analysis of two-dimensional soil layer based on Darcian flow will overestimate the consolidation rate. In addition, compared with Biot′s consolidation theory, the local pore pressure increase in the initial stage of consolidation under strip load is not obvious in the Terzaghi consolidation theory framework. The research results can provide a theoretical basis for exploring a more accurate settlement prediction method for saturated cohesive soil layer.
Keywords:
foundation engineering; plane-strain consolidation; saturated cohesive soil; Hansbo′s flow; finite volume method
由于Terzaghi一维固结理论仅考虑了地基的竖向渗流,按此理论对饱和黏性土地基中整体孔压的消散速率进行预测时常常得到偏慢的结果,所以不断有学者对其进行改进。1936年,
RENDULIC[1]假定地基中任意点的总应力之和不随固结时间而改变,将其扩展为二维和三维固结理论。1941年,BIOT[2]则在同时满足平衡微分方程、本构方程、几何方程以及孔隙水渗流连续性条件的基础上,得出了更为严格的真三维固结理论。不过,Biot固结方程求解较为困难,而Terzaghi-Rendulic固结方程则因其求解方便应用较为普遍,因此有学者对后者进行了深入研究。黄传志[3]、折学森[4]和李秉宜等[5]先后采用积分变换法、Green函数法等分别给出了二维Terzaghi-Rendulic固结微分方程的通解,并针对一些特殊情况给出了简化计算结果;雷国辉等[6]、CHEN等[7]和裴美娟等[8]先后研究了砂垫层、分布式排水边界和土体各向异性等因素的影响。但按上述理论对地基固结速率的预测结果经常与实际观测数据存在较大误差。这在一定程度上可归结为上述理论的基本假定与实际工程有一定偏离。
虽然一般固结理论都假定地基中的渗流符合Darcy定律,但室内试验和现场观测表明,饱和黏性土中的渗流速度v与水力坡降i之间并不总是直线关系。为描述这种非线性渗流,HANSBO[9]引入了分段函数:
式中:m为描述低速渗流时幂函数的指数;k为高速直线渗流段的渗透系数;i1为曲线渗流段和直线渗流段的分界起始水力坡降。很明显,Darcy渗流是Hansbo渗流的特例。只要m=1或i1=0,式(1)就退化为Darcy渗流方程。
为考查式(1)所示非Darcy渗流模式对饱和黏性土地基固结过程的影响,刘忠玉等[10]、鄂建等[11]和XIE等[12]先后将式(1)代替Darcy渗流方程,对Terzaghi一维固结方程进行了修正,结果表明与Darcy渗流相比,按Hansbo渗流计算时地基的一维固结进程将会延迟。实际上,考虑Hansbo渗流[13]或其他形式的非Darcy渗流[14]对砂井地基的固结分析也可得到类似的结论。
为进一步分析非Darcy渗流对平面应变固结过程的影响,本文引入式(1)描述黏性土地基中孔隙水的流动,在Terzaghi-Rendulic固结理论框架内,重新推导平面应变固结微分方程,并初步分析相关渗流参数对二维固结进程的影响规律。
1 平面应变固结方程推导
采用和Terzaghi-Rendulic固结方程一样的推导过程,可得Hansbo渗流条件下平面应变固结方程:
式(4)的初始条件:
u(x,z,0)=u0(x,z),(5)
式中,初始超静孔压u0(x,z)可取为外荷载p0作用下的平均附加应力,即u0(x,z)=(σx+σz)/2。其中σx和σz为外荷载p0作用下在点(x,z)处产生的x向和z向的附加正应力。
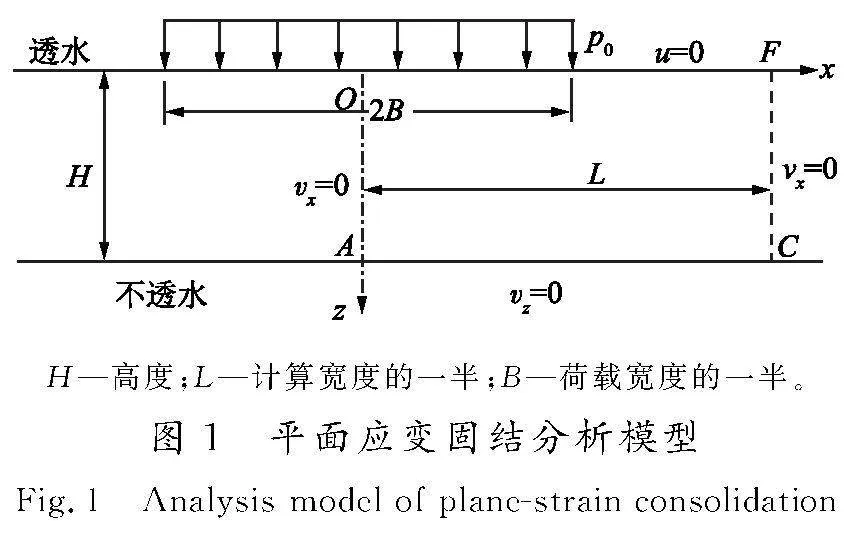
当地面荷载均布时,考虑对称性,对地基进行分析。式(4)的边界条件如下:
u(x,0,t)=0,(6)
vz(x,H,t)=0,(7)
vx(0,z,t)=0,(8)
vx(∞,z,t)=0。(9)
2 有限体积法求解
取图1中的F点足够远,比如L=5H,并用线段CF代替远端边界。将计算区域OACF用Δx和Δz分别沿x和z方向均分为M层和N层,共分为N×M个单元。在每个单元中心设置节点,并对时间按Δt进行离散。然后在任一时间段[tj,tj+Δt]内,对式(4)在任一单元(l, n)内积分:
用向前差分表示等号右边u关于时间t的偏导,将式(10)改写为
式中:R0,L0,B0,T0分别代表单元(l, n)的右、左、下和上4个边界。
用中间差分近似表示式(11)中关于x和z的偏导,并以全隐格式表示时间段[tj,tj+Δt]内的孔隙水压力,则
单元(l, n)的水力坡降分量ix和iz可分别取其左右边界和上下边界处对应值的平均值,计算单元(l, n)的水力坡降模,由式(3)求得该单元的视渗透系数K。而式(12)中单元边界处的视渗透系数K则可取相应边界2边单元视渗透系数的平均值。
离散后的初始条件可表示为
与边界条件式(6)-式(9)对应的离散方程为
将式(13)-式(19)代入式(12),形成封闭方程组,可用迭代法求解。
引入平均固结度Ut反映二维地基中超静孔压的整体消散速率和地基的固结程度
式中: D表示整个计算区域;ΔAl,n为单元(l,n)的面积,ΔAl,n=ΔxΔz;ujl,n和u0l,n分别为单元(l, n)在相应计算时刻j和初始时刻的超静孔压。
3 解法验证
3.1 考虑Hansbo渗流的一维固结
刘忠玉等[10]曾用有限体积法求解过考虑Hansbo渗流影响的一维固结方程。如将B取为无限大,即假定荷载p0均布于整个地基表面,那么二维固结将退化为一维固结。为便于讨论,引入无量纲参数:
式中,Tv为无量纲时间。
为说明本文方法的有效性,按二维固结进行分析,即取H=10 m,L=50 m,均布整个地面的荷载p0=100 kPa,mv=0.2 MPa-1,k=0.025 m/a,N=50,M=250,Δx=Δz=0.2 m,ΔTv=10-5。取不同的Hansbo渗流参数,分别分析地基平均固结度与时间的关系,结果如图2所示。为便于对比,图2中附上了刘忠玉等[10]的一维固结计算结果。很明显,二者几乎完全重合。
3.2 基于Darcy渗流的平面应变固结
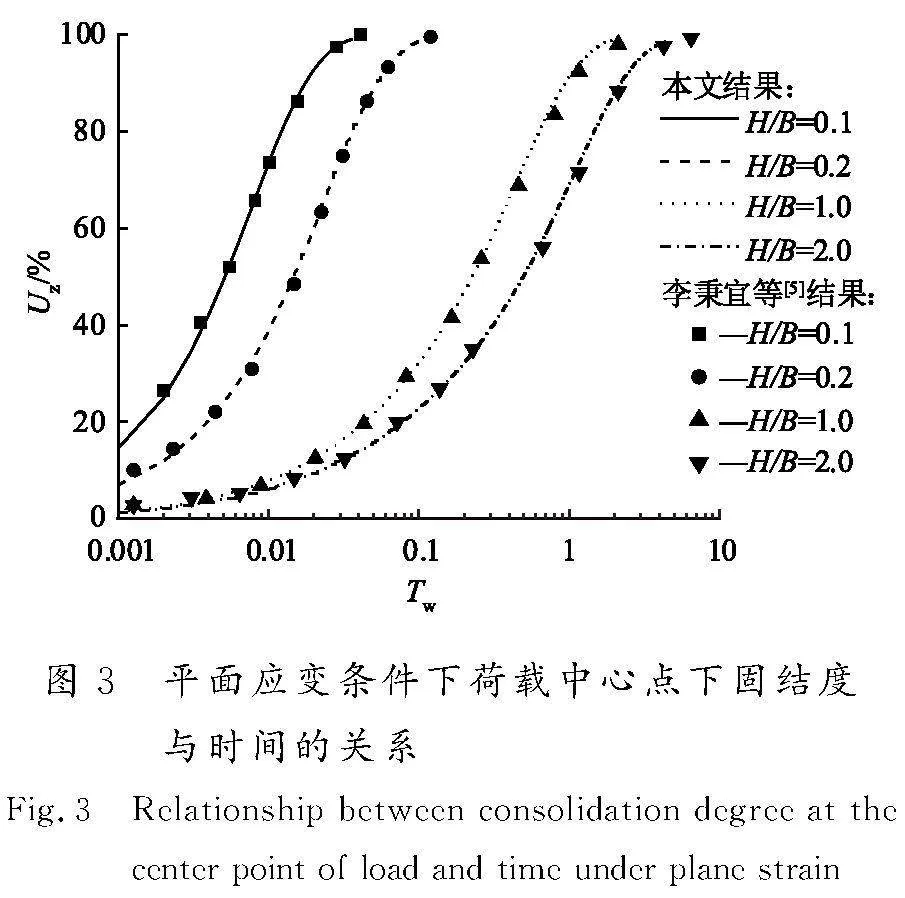
李秉宜等[5]曾采用 Green 函数法求解二维固8d484c5823bd6838a86e29fd42a4e96fe1c55682cbbb578f9f1b5c668dfe7fa5结微分方程,分析了Darcy渗流土层厚度对荷载中心点下固结度Uz的影响,并与GIBSON等[15]不考虑侧向变形(即泊松比μ=0)时,按Biot固结分析的结果进行了对比。这里取B=10 m,且H/B=0.1,0.2,1和2(其他参数同前)分析了荷载中心点下固结度Uz与时间的关系,结果如图3所示,其中无量纲时间Tw=Cvt/B2。为便于对比,图中附上了李秉宜等[5]的计算结果。从图3可以看出,当Tw较小时,本文结果略小于李秉宜等[5]的结果,而在TB>0.01时,二者则较为一致。
4 参数分析
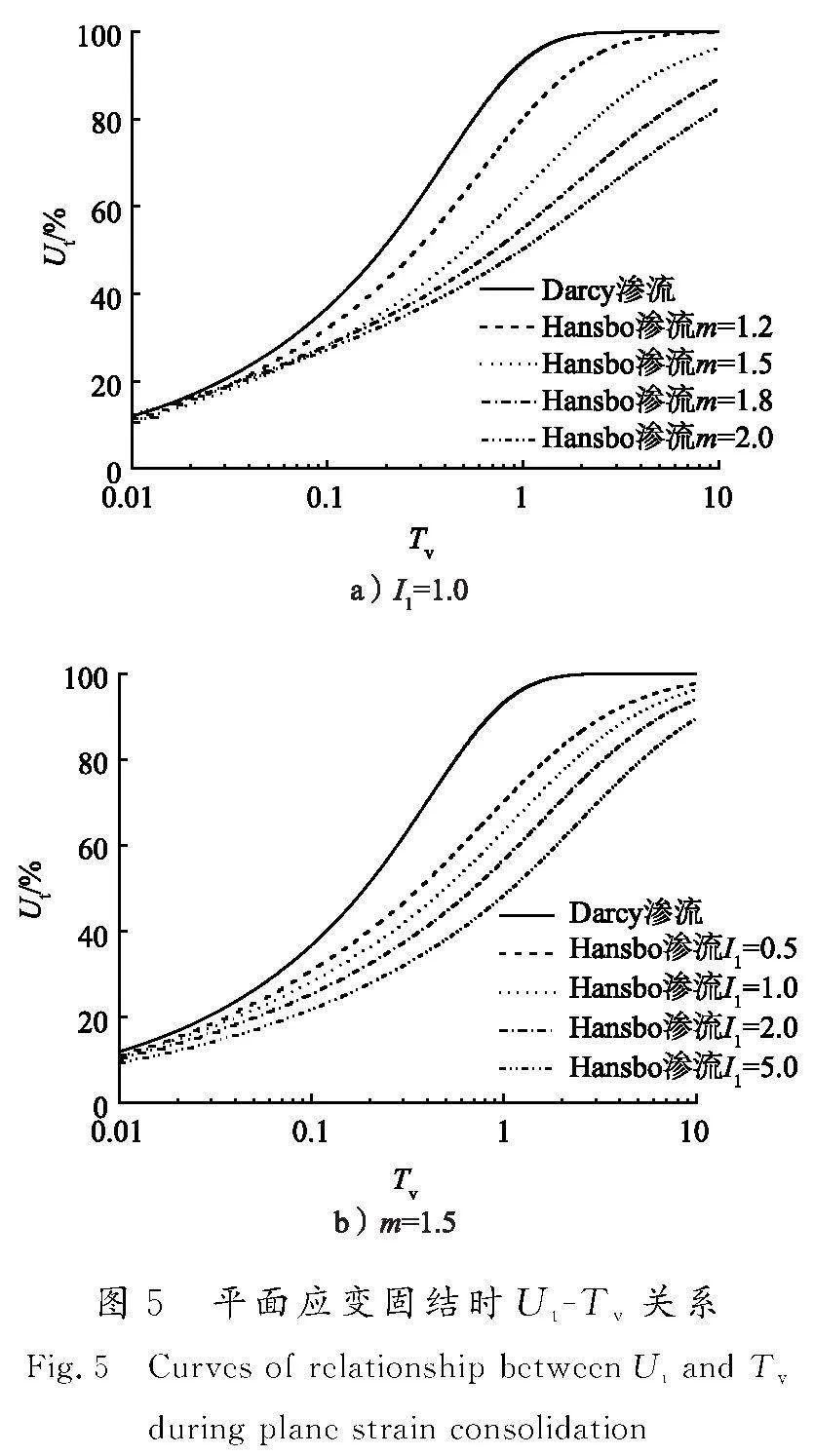
不失一般性,进行分析时取H=2B=10 m,L=50 m,mv=0.2 MPa-1,k=0.025 m/a,p0=100 kPa,N=50,M=250,Δx=Δz=0.2 m,ΔTv=10-5。另外,由文献[15]中Hansbo渗流参数的试验结果和分析用值可以发现,m值为1~2,i1为0~20,所以,进行单因素分析时,分别取m=1.2,1.5,1.8和2.0,I1=0.5,1.0,2.0和5.0。
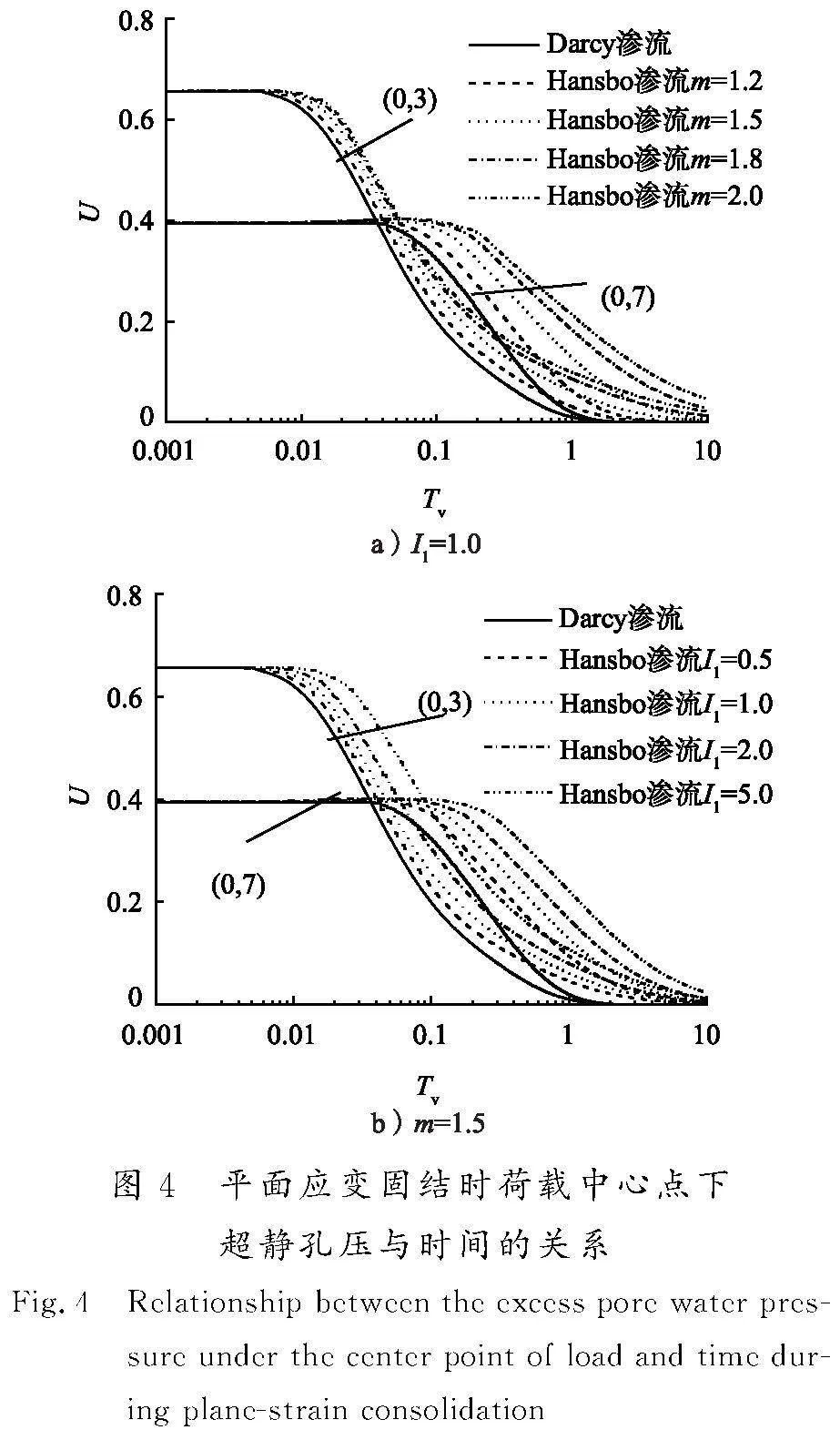
4.1 Hansbo渗流对孔压变化的影响
平面应变固结时荷载中心点下深3 m和7 m处超静孔压(U,U=u/p0)与时间的关系曲线见图4。由图4可知,在固结初期,同一位置处的各条曲线几乎重合,并稍微上扬。这说明该段时间内超静孔压值随时间略有增大,但最大增大值约为初始值的2%。刘忠玉等[16]也曾对类似工况利用有限元法进行过Biot固结分析,其固结初期超静孔压出现了随时间延长而增大的现象,且十分明显。根据其计算结果,当弹性模量E=7.2 MPa,泊松比μ=0.3,m=1.5,且 I1 分别等于0,0.5,1.0,2.0和 5.0 时,荷载中心点下深3 m处固结初期超静孔压达到的最大值分别比初始值增大4.3%,5.4%,6.1%,6.9%和7.2%。XU等[14]对砂井地基进行黏弹塑性固结分析时也发现固结初期超静孔压异常增大的现象。
以上3种情况对应的固结初期超静孔压增大程度之所以不同,是因为它们产生的机制不同。黏弹塑性砂井地基固结初期的孔压异常增大是由于土体黏滞性或时间效应引起的[14],二维Biot固结初期的孔压异常增高现象应归结为Mandel-Cryer效应[16],而这里固结初期超静孔压稍微增大的原因则是由于荷载中心点下的初始超静孔压呈上大下小分布,向下的渗流使得下部的超静孔压有所增大所致。
图4表明,与Darcy渗流相比,Hansbo渗流对应曲线的起始平缓段较长,且曲线段都在Darcy渗流对应曲线的上方,即后者延迟了地基中超静孔压的消散,而且Hansbo渗流参数m和I1越大,超静孔压开始消散的时间就越晚,随后消散速率也就越慢。以图4 b)为例,在Darcy渗流时,荷载中心点下7 m深度处的超静孔压由最初的0.39p0消散到0.20p0,需要的无量纲时间为0.23。在Hansbo渗流模式下,对应m=1.5以及I1=0.5,1.0,2.0和5.0,相应需要的无量纲时间则分别为0.39,0.54,0.76和1.20,即分别为Darcy渗流模式下所需时间的1.7倍、2.3倍、3.3倍和5.2倍。所以,在平面应变固结分析时,也应考虑非Darcy渗流的影响,否则将会得到比实际偏大的超静孔压消散速率。
4.2 Hansbo渗流对平均固结度的影响
为分析Hansbo渗流模式对平面应变固结时地基固结速率的影响,图5给出了不同I1或m时的平均固结度Ut与无量纲时间Tv的关系曲线。与Hansbo渗流对一维固结[10-12]、砂井地基固结[13-14]和二维Biot固结[16-17]的影响结论相似的是,考虑Hansbo渗流的Ut-Tv曲线均位于考虑Darcy渗流的曲线下方,并且Hansbo渗流参数I1或m越大,这些曲线与考虑Darcy渗流的曲线之间的距离就越大。也就是说,在Terzaghi固结理论框架内,按Hansbo渗流计算的平面应变地基的固结速率要比按Darcy渗流计算的要慢。以固结度达到85%为例,按Darcy渗流计算,需要的无量纲时间Tv=0.68,而考虑Hansbo渗流时,对应I1=1.0,且m=1.2,1.5,1.8和2.0的无量纲时间Tv分别为1.11,2.32,4.90和8.14,分别是前者的1.6倍、3.4倍、7.2倍和12.0倍。因此,和一维固结、砂井地基固结以及Biot固结分析类似,平面应变固结分析时也应考虑饱和黏性土地基中存在的渗流偏离Darcy定律的现象,否则可能会得到比实际偏快的地基固结速率。
5 结 语
本文引入Hansbo渗流方程代替Darcy定律来描述饱和黏性土弹性地基中的非线性渗流,在平面应变条件下对Terzaghi-Rendulic二维固结方程进行了修正,并采用有限体积法进行了数值求解,得到如下结论。
1)不论基于Darcy渗流还是Hansbo渗流,条形荷载下固结初期局部地基内的孔压增大现象并不明显,其最大增大量仅为初始值的2%左右。
2)与Darcy渗流相比,按Hansbo渗流计算时单个点的超静孔压开始消散的时间相对延迟,并且随着Hansbo渗流参数m和I1的增大,超静孔压的消散都趋于更加缓慢。
3)与Darcy渗流相比,按Hansbo渗流算得的平面应变地基的整体超静孔压消散速率偏慢。以平均固结度达到85%计算,在本文的计算范围内,按Hansbo渗流计算,需要的时间可延长至Darcy渗流的12.0倍。所以,按Darcy渗流计算时将会高估二维地基的固结速率。
本文在假定土体线弹性变形的基础上,初步分析了非Darcy渗流对二维地基固结的影响规律。在后续研究中,将同时考虑非Darcy渗流和非线性变形的共同影响,以更全面地分析二维地基的固结特性,并为提出新的更有效的地基沉降预测方法提供理论基础。
参考文献/References:
[1] RENDULIC L.Porenziffer und porenwasserdruck in tonen[J].Der Bauingenieur,1936,17:559-564.
[2] BIOT M A.General theory of three-dimensional consolidation[J].Journal of Applied Physics,1941, 12(2):155-164.
[3] 黄传志.多维太沙基固结微分方程求解[J].岩土工程学报,1991,13(1):34-47.
HUANG Chuanzhi.A solution of Terzaghi′s multidimensional consolidation differential equation[J].Chinese Journal of Geotechnical Engineering,1991,13(1):34-47.
[4] 折学森.二维太沙基固结微分方程求解[J].西安公路交通大学学报,1996,16(1):8-12.
SHE Xuesen.Solution to Terzaghi′s two-dimensional consolidation differential equation[J].Journal of Xi′an Highway University,1996,16(1):8-12.
[5] 李秉宜,王唤唤,刘旭.采用Green函数法求解二维固结微分方程[J].科学技术与工程,2023,23(17):7485-7493.
LI Bingyi,WANG Huanhuan,LIU Xu.Solving two-dimensional consolidation differential equation by Green function method[J].Science Technology and Engineering,2023,23(17):7485-7493.
[6] 雷国辉,李赞,徐梨丹.含砂垫层地基二维固结自由应变解[J].岩土工程学报,2016,38(2):193-201.
LEI Guohui,LI Zan,XU Lidan.Free-strain solutions for two-dimensional consolidation with sand blankets[J].Chinese Journal of Geotechnical Engineering,2016,38(2):193-201.
[7] CHEN Zheng,NI Pengpeng,CHEN Yifeng,et al.Plane-strain consolidation theory with distributed drainage boundary[J].Acta Geotechnica,2020,15(2):489-508.
[8] 裴美娟,杨鹏,李乐晗.二维固结过程中土体各向异性影响的研究[J].山西建筑,2022,48(17):96-99.
PEI Meijuan,YANG Peng,LI Lehan.Study on the influence of soil anisotropy during two-dimensional consolidation[J].Shanxi Architecture,2022,48(17):96-99.
[9] HANSBO S.Consolidation of Clay With Special Reference to Influence of Vertical Sand Drains[D].Stockholm:Swedish Geotechnical Institute,1960.
[10]刘忠玉,孙丽云,乐金朝,等.基于非Darcy渗流的饱和黏土一维固结理论[J].岩石力学与工程学报,2009,28(5):973-979.
LIU Zhongyu,SUN Liyun,YUE Jinchao,et al.One-dimensional consolidation theory of saturated clay based on non-Darcy flow[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(5):973-979.
[11]鄂建,陈刚,孙爱荣.考虑低速非Darcy渗流的饱和黏性土一维固结分析[J].岩土工程学报,2009,31(7):1115-1119.
E Jian,CHEN Gang,SUN Airong.One-dimensional consolidation of saturated cohesive soil considering non-Darcy flows[J].Chinese Journal of Geotechnical Engineering,2009,31(7):1115-1119.
[12]XIE Kanghe,WANG Kun,WANG Yulin,et al.Analytical solution for one-dimensional consolidation of clayey soils with a threshold gradient[J].Computers and Geotechnics,2010,37(4):487-493.
[13]刘忠玉,焦阳.基于Hansbo渗流的理想砂井地基固结分析[J].岩土工程学报,2015,37(5):792-801.
LIU Zhongyu,JIAO Yang.Consolidation of ground with ideal sand drains based on Hansbo′s flow[J].Chinese Journal of Geotechnical Engineering,2015,37(5):792-801.
[14]XU Chuanyong,LIU Zhongyu,ZHANG Jiachao,et al.Analysis of large-strain elastic viscoplastic consolidation for soft clay with vertical drains considering non-Darcian flow[J].Applied Mathematical Modelling,2021,92:770-784.
[15]GIBSON R E,SCHIFFMAN R L,PU S L.Plane strain and axially symmetric consolidation of a clay layer on a smooth impervious base[J].Quarterly Journal of Mechanics and Applied Mathematics,1970, 23(4):505-520.
[16]刘忠玉,张家超,郑占垒,等.考虑Hansbo渗流的二维Biot固结有限元分析[J].岩土力学,2018,39(12):4617-4626.
LIU Zhongyu,ZHANG Jiachao,ZHENG Zhanlei,et al.Finite element analysis of two-dimensional Biot′s consolidation with Hansbo′s flow[J].Rock and Soil Mechanics,2018,39(12):4617-4626.
[17]邓岳保,谢康和,李传勋.考虑非达西渗流的比奥固结有限元分析[J].岩土工程学报,2012,34(11):2058-2065.
DENG Yuebao,XIE Kanghe,LI Chuanxun.Finite element analysis of Biot′s consolidation with non-Darcian flow[J].Chinese Journal of Geotechnical Engineering,2012,34(11):2058-2065.

