基于分集的非相干多进制正交调制迭代译码研究

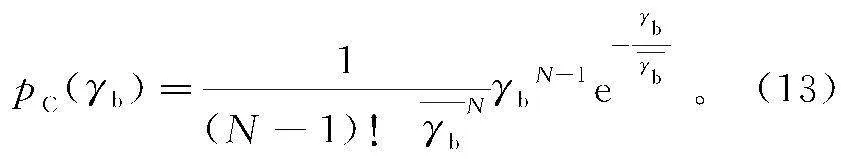
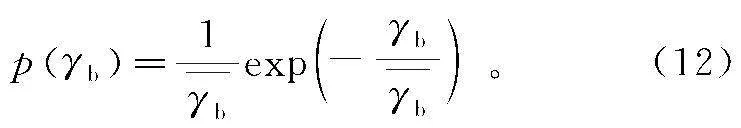
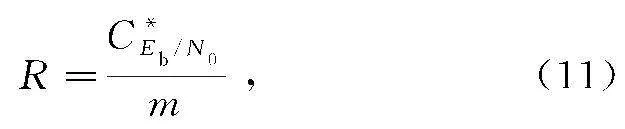
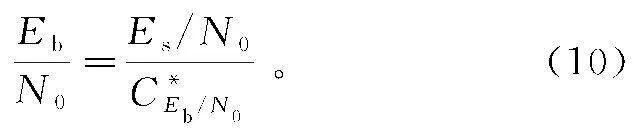
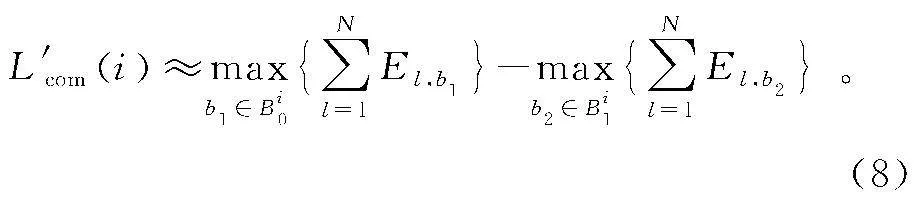
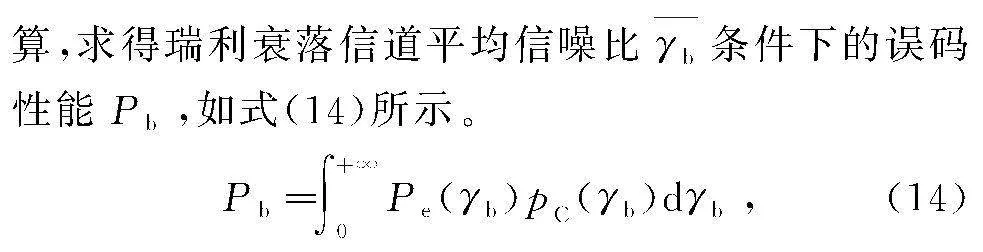
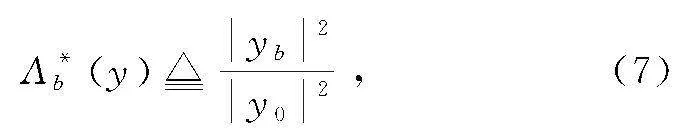
摘 要：为了解决无线通信系统低速率传输面临的瞬时快衰落明显、归一化多普勒很大、接收信号弱等多种难题，提出了基于分集的非相干多进制正交调制迭代译码体制。首先，构建了非相干多进制正交调制迭代译码模型，给出了基于最大值映射的简化解调译码方法；其次，设计了基于分集的非相干多进制正交调制迭代译码系统方案，分析了信道容量极限关键参数，推算出编码码率与信噪比关系，提出了基于分集合并信号概率密度的性能分析方法；最后，采用蒙特卡洛仿真方法，结合高斯信道与瑞利衰落信道进行了系统仿真验证及性能分析。结果表明：在归一化多普勒0.5的瑞利衰落信道仿真环境下，采用16重分集、32阶正交调制、Turbo/低密度奇偶校验码（LDPC）迭代译码，编码码率为2/3、编码信息长度为384的设计方案，可实现信噪比低至3 dB时的稳定通信。所提出的基于分集的非相干多进制正交调制迭代译码方法，实现了低信噪比高可靠传输，可为低速率无线通信系统设计提供参考。

关键词：无线通信技术；多进制正交；非相干；瑞利信道；分集；概率密度

中图分类号：TN914.3 文献标识码：A

Non-coherent M-ary orthogonal modulation and iterative

decoding research with diversity

Abstract：

In order to solve the various difficulties of low speed wireless communication， such as instantaneous fast fading， doppler spread and weak signal， a technical system of non-coherent M-ary orthogonal modulation and iterative decoding with diversity was proposed. Firstly， a system model of non-coherent M-ary orthogonal modulation was constructed， and a simplified demodulation and decoding based maximum mapping method was proposed. Secondly， the system scheme of non-coherent M-ary orthogonal modulation and soft iterative decoding with diversity was designed， and the key parameters for channel capacity limit was analyzed. The relationship between code rate and signal-to-noise ratio（SNR）was derived， and the performance analysis method of probability density with diversity merging signal was studied. Finally， using Monte Carlo simulation method， the system capacity performance was simulated and analyzed in AWGN channel and Rayleigh channel.The results indicate that using 16 diversity， 32-ary orthogonal modulation， Turbo or LDPC iterative decoding， code rate of 2/3 and length of 384， the stable communication is achieved at the SNR of 3 dB in Rayleigh channel with the normalized doppler 0.5. The proposed method achieves reliable transmission with low SNR， which provides reference for the design of low-speed wireless communication system.

Keywords：

wireless communication technique; M-ary orthogonal; non-coherent; Rayleigh channel; diversity; probability density

无线通信系统应用于中国众多行业与领域，实现多种类业务、多区域信息可靠通联。在关键业务通信保障场景下，无线通信系统应具有更高通信可靠度；在高原山区通信保障场景下，应能适应更加复杂的地理环境。针对高可靠度、复杂地形环境应用需求，亟需开展低速率通信波形研究，实现无线通信链路高可靠、全环境联通能力。低速率通信设计面临瞬时快衰落明显、归一化多普勒很大、接收信号微弱等多种技术难题，国内外学者在此方面已开展了前期研究[1-4]。文献[5]通过高动态下大多普勒频移对数字相位调制信号的量化分析，表明差分相移键控（DPSK）调制误码性能随着多普勒增加而出现明显恶化。文献[6]研究了衰落信道中多普勒频移对于DPSK调制方式的影响，系统性能随多普勒变大而明显下降的问题。由此可见，常规中高速率传输采用的PSK调制方式难以适用于低速通信波形，多普勒效应导致误码性能急剧恶化甚至不能有效联通，无法实现低速率低门限可靠通信。

多进制正交调制方式具有误码性能好、抗频偏能力强等优点，能够通过增加信号带宽、优化调制阶数来实现误码性能改进。因此，在信道频带资源相对充足、信道功率严重受限的低速率无线通信系统中，多进制正交频率调制、正交扩频调制、LoRa（long range radio）调制等成为较佳选择。文献［7］—［9］研究了多进制频移键控（MFSK）调制方式在极低速通信中的性能，验证了其克服多普勒频移的有效性，但未结合软判决译码迭代设计，无法实现极低门限信噪比下可靠通信。文献［10］—［11］给出了多进制扩频检测的比特软值输出计算方法，仿真分析了多进制扩频结合Turbo乘积码的误比特率性能，验证了比特软值输出迭代译码的有效性，但未采取多重分集接收联合设计，难以实现衰落信道低门限接收。文献[12]提出了多进制扩频系统方案，针对硬判决解调方式开展仿真，给出误比特性能与信噪比的关系，但未将多进制调制与软判决译码进行联合设计。文献[13]研究了MFSK针对合并信号结合里德-所罗门（RS）编码的设计方案，尚未实现多重分集软迭代译码接收，难以实现衰落信道下低信噪比、极弱信号接收。文献[14]通过LoRa调制方式实现了频率选择性衰落信道环境下的多点组网设计，但未充分研究大归一化多普勒下的超低门限设计与实现方法。

现有多进制正交调制技术尚未实现多重分集与软判决迭代译码联合设计，难以满足低速率通信下抗瞬时快衰落、抗动态大多普勒、超低接收门限要求。本文采用多进制正交调制、多重分集接收、软判决迭代译码联合设计方案，通过信道容量极限参数分析指导编码码率选用，采用基于分集概率密度分析方法实现调制阶数与编码参数的整体优化，实现了瑞利衰落信道下低门限接收。

1 非相干多进制正交调制解调译码模型

1.1 迭代解调译码模型

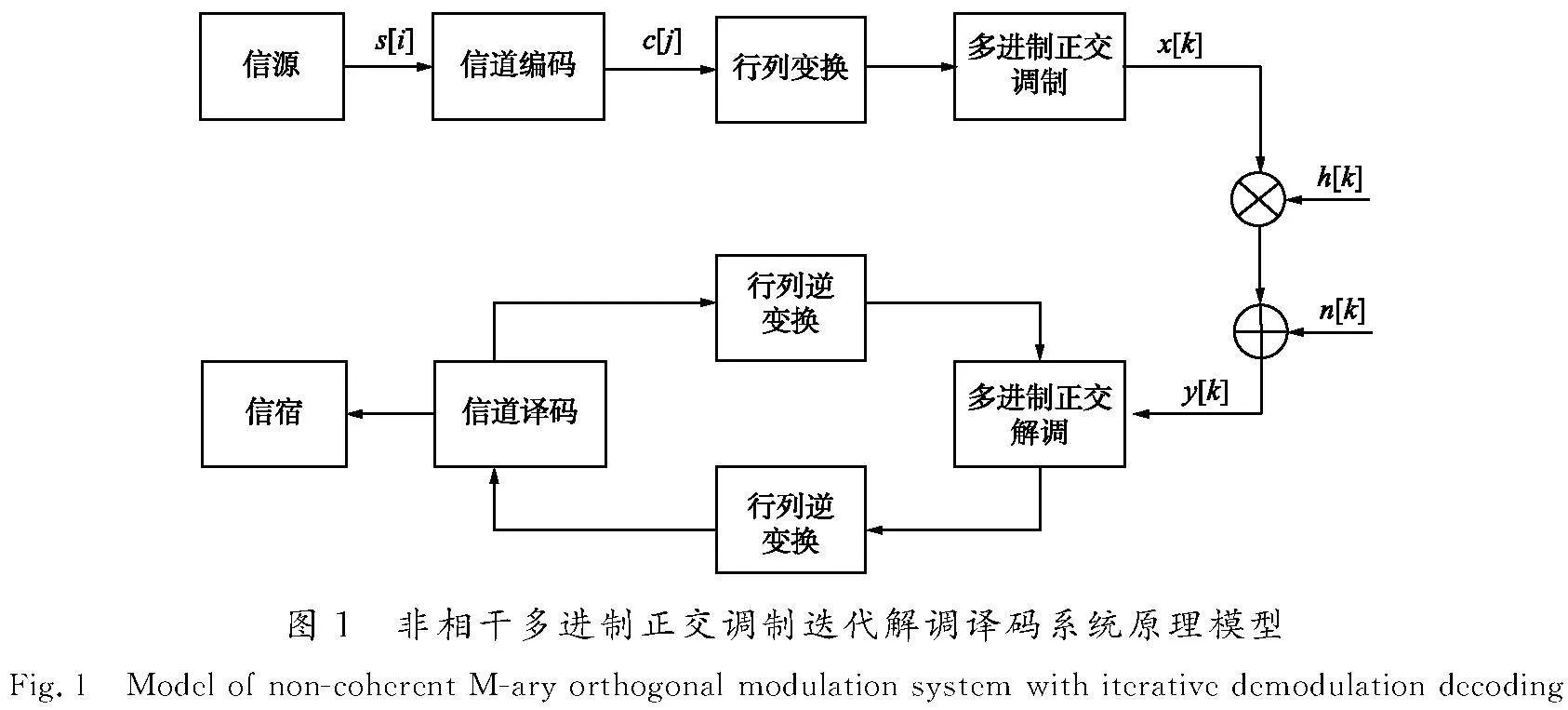
图1为非相干多进制正交调制迭代解调译码系统原理模型[15]。设正交调制阶数为M=2m，其中M表示正交调制频率或扩频符号数;m表示多进制调制符号对应的比特数，为不小于1的整数。信道编码码率为R，选用整数L作为发送正交调制符号数，则可设发送二进制比特数RLm的信息流为s（i）（i=0，1，…，RLm－1）。经过近极限高效信道编码增加校验信息后可得到比特数Lm的传送信息流c（j）（j=0，1，…，Lm－1）[16]。编码后比特信息映射为正交扩频符号，M进制正交调制输出M进制向量x（k）（k=0，1，…，L－1），设xb（k）表示M个调制符号中对应的某一个正交频率或扩频符号等分量信息，调制输出集合形成为ε=eb：b=0，1，…，M－1，其中eb为第b个分量信息为1或全部为0的典型基本向量。

编码序列c（j）中m个比特，变换形成一个多进制调制符号，对应的信道输出表示为

非相干检测接收机针对每个正交调制分量进行能量检测，对应检测结果设为yb2，对应理想信道容量C的计算公式如式（2）[17]所示。

式中：I0·为第1类零阶贝塞尔函数；Es，N0，a，yb均与前相同。

由于上述运算涉及的Es，N0，a参数值通常存在估算误差，导致传送信号与接收信号存在失配，实际信道容量C*根据式（4）[18]计算。

1.2 简化解调译码模型

非相干多进制正交调制迭代解调译码软信息计算，依赖于a（k），Eb，N0等信道状态先验信息，为降低工程实现复杂度，尽量简化信道状态信息[19-20]。接收端采用最大值映射法针对正交解调输出信息进行计算[21]，每个正交解调符号第i比特软信息计算如式（5）所示。该比特软信息计算结果L′di形成多进制符号中第i比特译码软信息，馈送给后端译码器。

针对该简化解调译码方法的参数关系进行分析，设发送信号为eb时接收信号为y，采用yi表示接收信号第i个正交分量，则接收信号对应信道传输概率为

该种简化方法信道容量见式（4），其中接收信号似然比Λ*by如式（7）所示。

式中：y0表示全0时对应的正交分量。

由此可知，C*仅与接收信号y直接关联，且根据传输信道容量上限为C，则C*≤C。

2 基于分集的非相干多进制正交调制迭代译码系统设计

2.1 系统实现方案

在无线传播中信道呈现瑞利衰落特性，信号存在瞬时快衰落现象，并且出现多普勒扩展等变化。为克服瞬时快衰落通常综合采取时域、频域、空域联合分集技术，接收端通过多条分集支路合并能够大幅平滑快衰落，显著改善系统接收性能。在低速通信波形设计中，为克服多普勒效应，必须选用具有良好抗频偏特性、误码性能好的调制与检测方式。

针对以上特殊传输要求，设计基于分集的非相干多进制正交调制迭代译码系统方案，如图2所示。采用多进制正交非相干检测可实现极强的抗多普勒效果，利用有效重数的分集联合接收能够实现抗衰落能力，优化多进制阶数，级联设计软判决迭代译码，实现系统性能优化。

发送端将待发送信息进行缓存处理，缓存信息根据编码方式选择Turbo编码、LDPC编码等形成编码信息。该编码信息经过间隔比特数t的时域分集处理后可形成重复信息比特流，并与原信息比特流有序衔接，然后插入帧头形成编码帧，再经过串并变换处理可得到对应多进制阶数的多路并行码流信息，通过多进制正交调制形成基带调制信号，经由频域分集及空间分集发送可生成多个分集支路信号，最后分别选用不同空间发送信道进行无线信号传播。

在上述多进制正交过程中，正交频率调制时频率间隔可选用0.5倍信号带宽，正交扩频调制时可采用百倍至千倍扩频比，实际设计时根据系统带宽资源、实现复杂度等综合设计。

每个分集支路信号传播信道均为无线衰落信道，通常以瑞利信道最为典型，通过优化分集参数设计，确保获得足够的有效分集效果。

接收端同时接收来自多个分集支路的传输信号，多路分集信息分别送入多进制正交解调模块，均与多个已知正交序列信号进行能量相关匹配，可输出得到多路非相干检测的能量值E1，1，E1，2，…，E1，M，E2，1，E2，2，…，El，b，…，EN，M。将对应多个不同分集支路的能量检测值全部进行合并，得到E1，E2…，EM，再将合并结果送至择大判决模块，通过能量幅度比较选择最大值进行硬判处理得到B1，B2，…，Bi，…，BM。根据该硬判数据进行帧头序列匹配搜索实现帧定时捕获，并采用最大值映射法计算得到每位比特的软判决值，在帧同步控制下，经过时域分集信息合并处理后送给Turbo/LDPC迭代译码模块，通过多次循环迭代处理收敛至最佳译码结果，最后进行判决恢复比特码流，缓存处理后按需输出。

在上述接收端处理过程中，最大值映射软值是实现软迭代译码的重要步骤，通过多分集支路平方能量检测值合并结果，对应第i比特分别为0，1时搜索相应最大的检测合并值，二者之差则为合并信号软信息L′comi，具体计算公式如式（8）所示。

根据帧同步控制信号，调整对齐时间分集比特软信息，并进行软信息相加合并，如式（9）所示，得到译码输入比特软信息L′com-alli。

L′com-alli≈L′comi+L′comi+t，（9）

式中：t为时间分集间隔比特数，馈送至Turbo/LDPC迭代译码模块。

2.2 信道容量极限关键参数分析

非相干多进制正交调制迭代译码方案随着编码码率趋近于0，所需信噪比趋近无穷，在确定调制阶数条件下存在最佳码率，能够获得最优性能。首先，结合信道容量变化关系，确定编码码率R与信噪比Eb/N0的关系，其中Eb/N0表示比特归一化信噪比；然后，利用蒙特卡洛仿真，得到信噪比与编码码率的关系曲线，以此指导确定最佳码率。

信道容量极限关键参数分析具体步骤如下。

1）根据非相干多进制正交调制、简化解调译码模型，采用式（4）计算非相干多进制正交调制系统的实际信道容量C*。

2）根据第一步分析形成的C*，在比特信噪比Eb/N0时的信道容量比率表示为C*Eb/N0，亦即在最佳性能极限条件下一个多进制调制符号可传输的最多信息比特数，由此分析得到比特信噪比Eb/N0与符号信噪比Es/N0之间的换算关系，具体如式（10）所示。

3）利用Eb/N0与Es/N0之间的换算关系，通过蒙特卡洛仿真，分析给出信噪比与编码码率的关系图并确定最佳编码码率。

a） 对于可靠传输，系统编码码率R要满足式（11）。

式中：m表示多进制调制符号对应的比特数量。

b） 利用仿真与演算，得到归一化信噪比与高效信道编码码率之间的关系图，确定最佳编码码率。

2.3 瑞利衰落信道下误码性能分析方法建立

在无线衰落信道条件下，采用γb表示随机变化状态下的瞬时信噪比，其呈现瑞利分布特性，传输信号幅度变化服从瑞利分布，则信号能量变化（即为幅度平方）服从χ2分布，则γb为χ2分布，γb表示γb的平均值。根据χ2分布的概率密度函数特性，γb的概率密度函数pγb如式（12）[18-20]所示。

采用pC（γb）表示多重分集合并之后的概率密度，N个分集支路信号衰落相互统计独立，根据式（12）所示概率密度特性进行N重分集合并，可得

瑞利衰落信道接收信号瞬时信噪比不断变化，与恒参信道接收信噪比呈现固定不变状态（γb固定不变）完全不同，难以直接采取某固定值表示链路信噪比，为便于开展性能分析，将瑞利衰落信道划分成很多个信道区间，每个信道区间可等效为近似恒参信道，再将全部区间误码性能进行累加。综上，提出基于分集合并信号概率密度误码性能分析方法。

采用Pe（γb）表示AWGN信道条件下信噪比为γb时对应的误码差错概率，采用pC（γb）表示分集合并信号瞬时信噪比概率密度，通过概率积分计

式中：Pe（γb）与调制阶数、编码参数密切相关，可基于AWGN信道通过蒙特卡洛仿真得到误码差错概率。

基于分集合并信号概率密度的误码性能分析方法主要实现过程如下。

1）根据调制阶数、编码方式、编码码长等系统设计参数，通过蒙特卡洛仿真得到AWGN信道下的比特差错率曲线，针对相邻信噪比仿真数据进行线性内插，获得更高信噪比精度条件下的比特差错概率。

3）重复1）、2），更换调制阶数、编码方式、编码码长等系统参数，再次仿真计算其他参数下的系统误码性能。

4）对比不同系统设计参数时的误码性能差异，结合系统接收门限、带宽资源等实际应用需求，选择给出最佳参数设计与误码性能结果。

3 系统仿真验证与性能分析

3.1 高斯信道下编码码率极限仿真

结合非相干检测多进制正交调制容量极限关键参数分析方法，根据式（4）及式（11）所示计算关系，采用数值演算方法，仿真不同调制阶数时的编码码率极限参数。

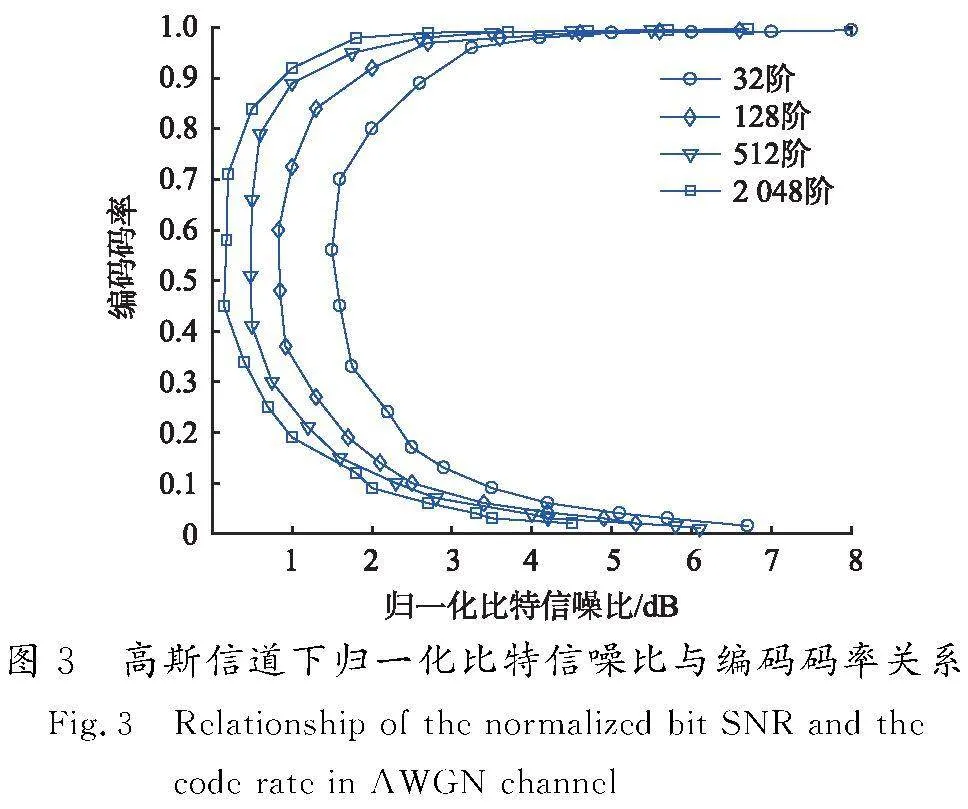
仿真选取AWGN信道条件，调制阶数选取4种典型值，分别为32，128，512，2 048，信噪比为0～8 dB，基本涵盖了涉及信噪比区间范围。

高斯信道下归一化信噪比与编码码率关系的仿真结果如图3所示。调制阶数逐渐增加，信噪比门限随之降低，但随着调制阶数增多可获得改善的程度越来越小。由图3可知，不同调制阶数曲线在相同编码码率时的信噪比差异，在编码码率为0.4～0.7时，从32阶增加至128阶时，信噪比门限可改善约0.5 dB，从128阶继续增加至512阶时可改善约0.3 dB。根据系统带宽资源、误码性能及实现复杂度的综合权衡分析，建议选用32阶调制。

编码码率在接近于0.5时具有较佳信噪比，在0.4～0.7时，能够获得较小的信噪比门限，建议选

用编码码率0.4～0.7作为系统设计参数。由于系统性能还与编译码方式、码字长度、码字性能等多种因素相关，最终编码码率可结合系统带宽、传输时延、实现复杂度等多种因素进一步择优设计。

3.2 高斯信道下系统性能仿真

采用蒙特卡洛仿真方法，构建高斯信道下非相干正交调制迭代译码仿真系统，发送端信息经过信道编码、非相干正交调制，经由高斯信道叠加噪声，接收端通过非相干检测、迭代译码处理后恢复原始信息，将发送端信息与接收端恢复信息进行对比，统计得到系统误码性能。

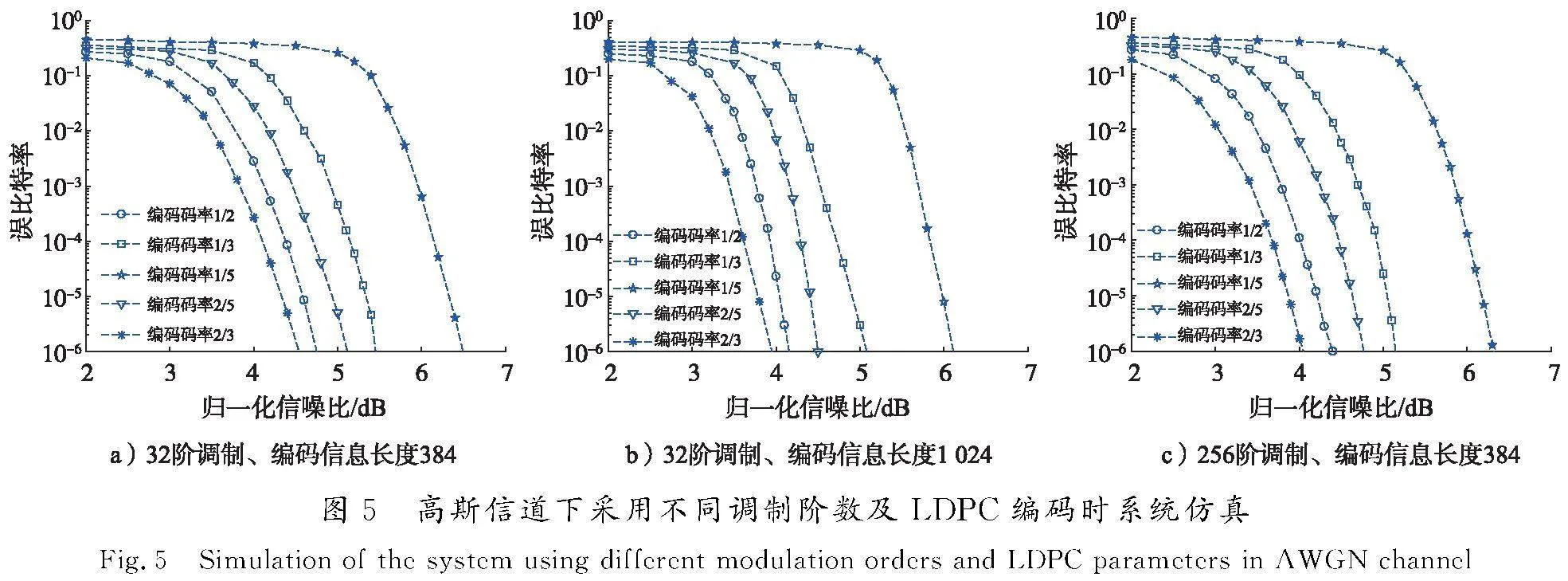
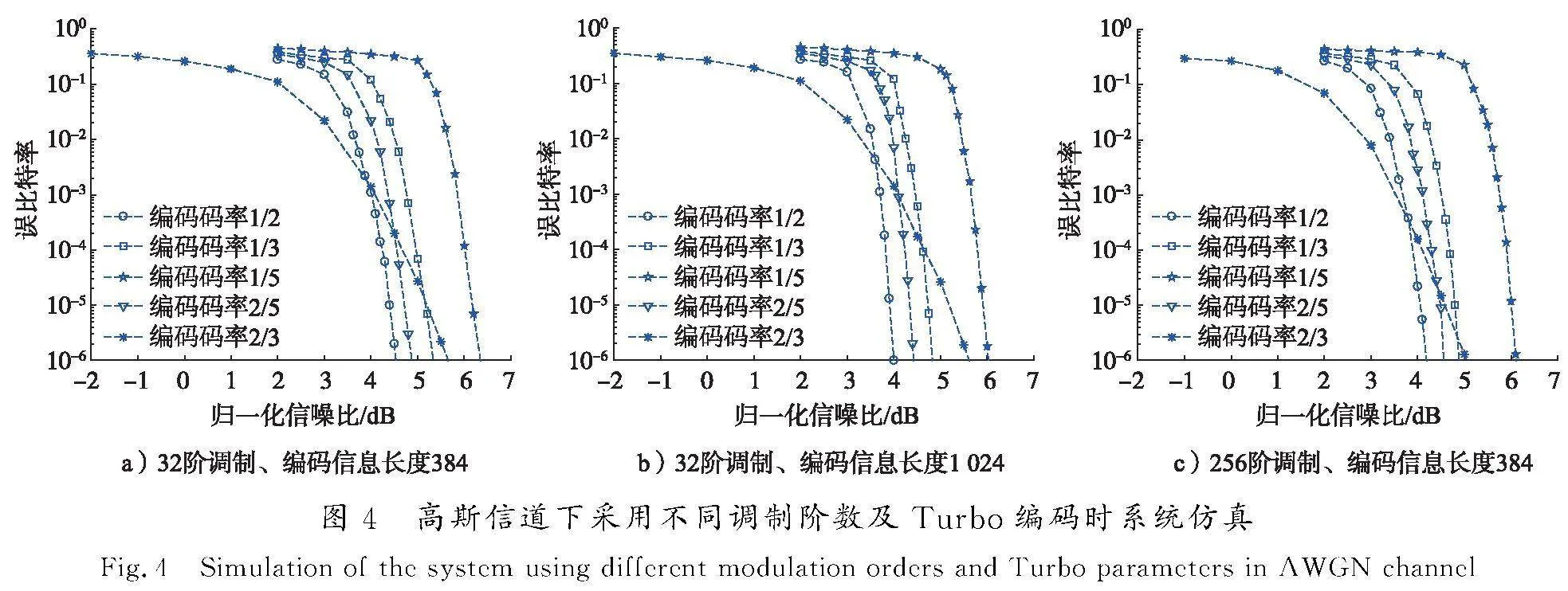
仿真条件选取如下：调制阶数为32，256；信道编译码分别选用Turbo码和LDPC码；编码信息长度为384，1 024；编码码率为1/5，1/3，2/5，1/2，2/3，覆盖了较低信噪比门限的主要范围（0.4～0.7）。Turbo编码为面向5G的增强型Turbo码，采用咬尾编码结构；译码采用Enhanced-Max-Log-MAP算法，选取校正因子0.75；LDPC编码采用5G LPDC编码方案（基于基矩阵BG1和BG2进行循环移位矩阵设计实现高效编码，适配支持不同信息位长度和码率参数）。

高斯信道下系统仿真结果如图4、图5所示。在调制阶数为32、编码信息长度为384及1 024时，Turbo码在编码码率为1/2时信噪比门限达到最佳，编码码率为2/3，2/5，1/3时信噪比门限略微变差，编码码率为1/5时信噪比门限变得最差；LDPC码在编码码率为2/3时信噪比门限达到最优，编码码率为1/2，2/5，1/3时信噪比门限逐渐变差，码率编码为1/5时信噪比门限变得最差。由此看来，不同编码码率对信噪比门限影响较大，编码码率为2/5，1/2，2/3均具有相对较低的信噪比门限。在相同编码方式、相同编码码率条件下，随着编码信息长度由384增加至1 024时，性能可提升0.4～0.6 dB。调制阶数由32增加至256时，根据图4 a）与图5 a）以及图4 c）与图5 c）的曲线对比，性能改善0.3～0.5 dB。

由上述仿真验证分析可知，调制阶数由32增加至256时，性能改善非常有限，但导致实现复杂度、带宽资源均呈现数量级增长，对于工程化实现造成巨大困难，因此建议选用32阶调制。按此分析，在调制阶数为32时，采用Turbo码、LDPC码高效编码，编码信息长度达到384，编码码率处于0.4～0.7，可实现较低的信噪比门限，为瑞利衰落信道下系统仿真提供数据参考。

3.3 瑞利信道下系统性能仿真

瑞利信道下系统性能仿真主要包括典型多普勒条件下系统性能仿真、各种设计参数下系统性能仿真2种。该仿真既充分验证多普勒适应能力，又全面验证各种参数性能优劣，为系统设计提供参考依据。

1）典型多普勒条件下系统性能仿真

采用蒙特卡洛仿真方法，构建瑞利衰落信道下基于分集的非相干正交调制迭代译码仿真系统，仿真系统组成参照图2，发送端经过信道编码、非相干正交调制，经过时域、空域、频域联合分集形成多路发送信号，经由多个相互独立的衰落信道传播，接收端通过非相干检测、分集合并、迭代译码处理后恢复得到原始信息，将发送端信息与接收端恢复信息进行对比，统计得到系统误码性能。

仿真条件选取如下：设置各个分集支路衰落特性相互独立；最大多普勒频移分别为1，10，20，30，50 Hz（对应归一化多普勒分别为0.01，0.10，0.20，0.30，0.50）；调制阶数选用32；分集方式选用4重时频分集×4重空间分集；信道编码选用Turbo码和LDPC码，具体编译码方案与“3.2”项下方案相同；编码信息长度为384；编码码率为2/3。

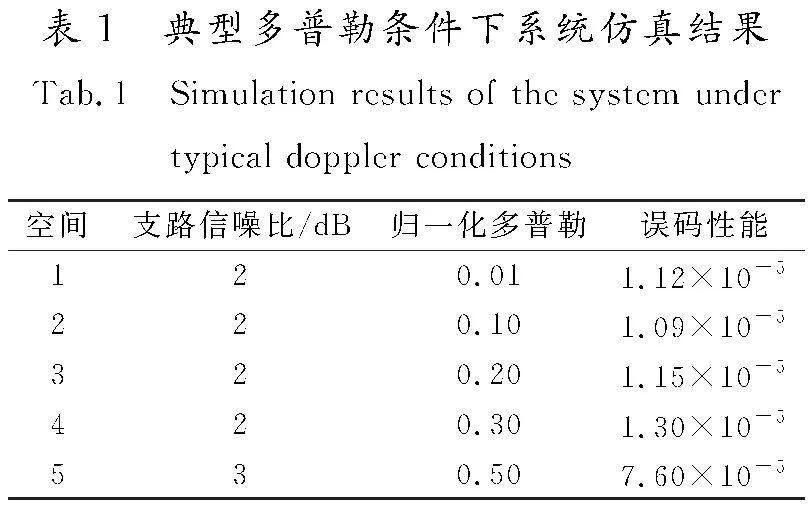
典型多普勒条件下系统仿真结果如表1所示。在每个空间支路信噪比为2 dB条件下，随着归一化多普勒由0.01增大至0.20，系统未出现性能损失，随着多普勒继续增大至0.50时，性能仅出现轻微下降，实现了良好的抗多普勒效应。

2）各种设计参数下系统性能仿真

采用数值仿真方法构建瑞利衰落信道下系统性能仿真模型，首先根据式（13）演算多重分集信号信噪比概率密度，其次采用图4、图5给出的误码性能作为瞬态误码性能，最后根据式（14）仿真瑞利衰落信道下的系统性能。

仿真参数选取如下：设置各个分集支路衰落特性相互独立；调制阶数选用32；分集方式选用4重时频分集×4重空间分集；信道编码选用Turbo码和LDPC码，具体编译码方案与“3.2”项下方案相同；编码信息长度选用384，1 024；码率选用1/5，1/3，2/5，1/2，2/3，覆盖了低信噪比门限范围（0.4～0.7）。

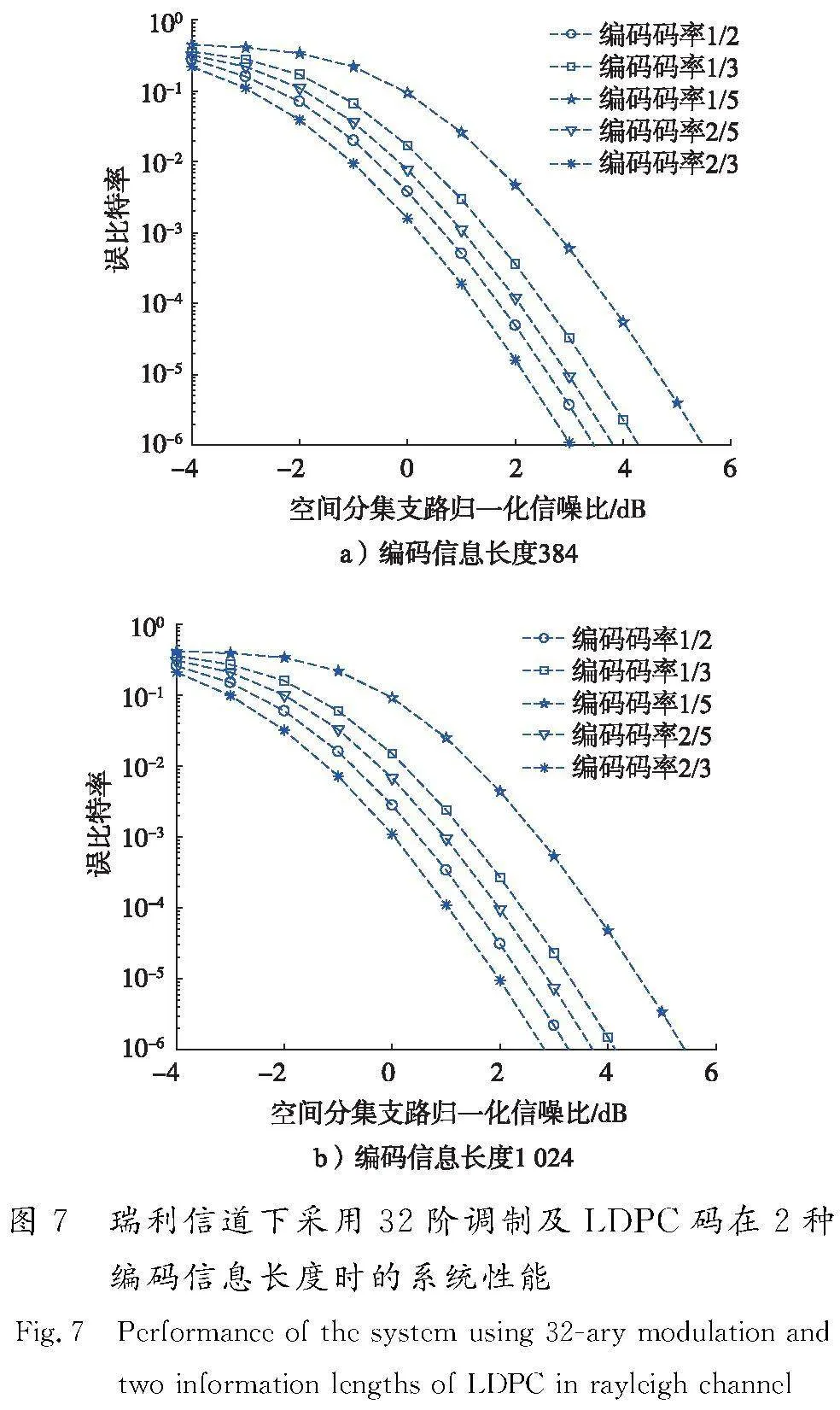
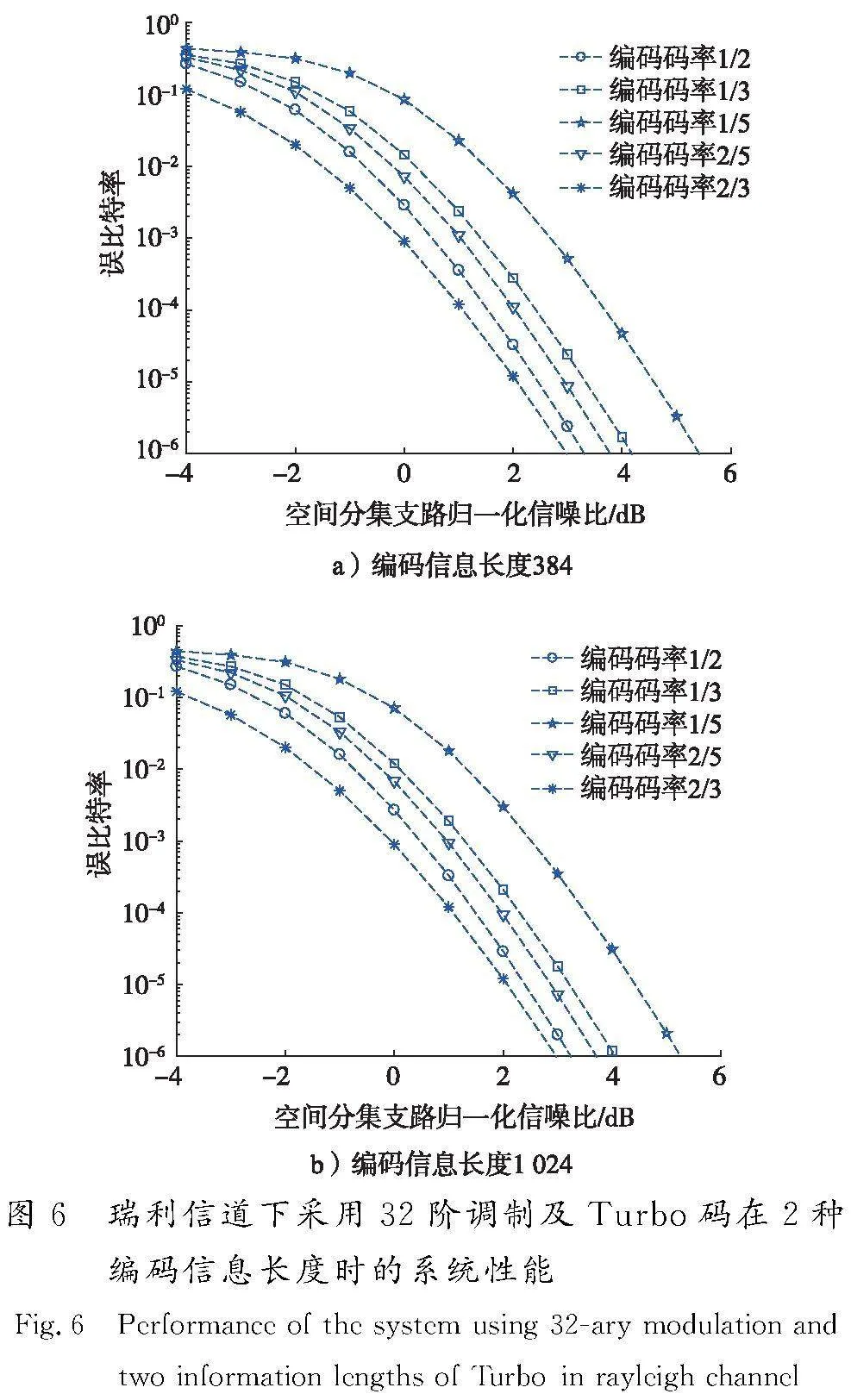
各种设计参数下系统仿真误码性能结果如图6、图7所示。采用Turbo码、LDPC码2种编码方式在相同码率、相同码长参数条件下的系统性能变化规律近似。在编码码率为2/3时信噪比门限达到最优；其次，编码码率由2/3变化至1/2，2/5，1/3时信噪比门限变差0.3～1.4 dB；再次，编码码率变化至1/5时信噪比门限恶化达2.5 dB。编码信息长度由384增加至1 024，相同有效分集重数条件下可获得增益约0.1～0.2 dB，相比AWGN信道下增益达0.4～0.6 dB，码长增加可获得的性能增益明显变小，主要由于瑞利衰落信道下分集接收后瞬时信噪比仍然存在一定波动，波动峰谷信噪比状态下的增益较小所致。

系统仿真结果为低速率无线通信系统设计提供了参数精准量化依据。无线低速系统采用多重分集合并信号最大值映射法支持Turbo/LDPC软译码，通过优化选用调制阶数、编码码率、编码信息长度等参数，在归一化多普勒为0.50的瑞利衰落信道条件下，实现每个空间分集支路平均信噪比约3 dB的低门限可靠接收，系统误码率低至10-6。

4 结 语

针对瑞利衰落信道多普勒效应导致低速通信性能恶化的问题，本文提出了一种基于分集的非相干多进制正交调制迭代译码方案，验证表明该方案能够适应快衰落、大多普勒的瑞利信道环境，给出了系统参数取值范围，实现了低信噪比高可靠传输，具体结论如下。

1）编码码率为0.4～0.7时，系统具有较低的信噪比门限。

2）在瑞利衰落信道条件下，编码码率为2/3时系统信噪比门限最优，当编码码率由2/3降低至1/2，2/5，1/3，1/5时性能变差0.3～2.5 dB；编码信息长度由384增加至1 024时，系统性能增益提升0.1～0.2 dB。

3）无线低速率通信系统，在归一化多普勒为0.5的瑞利衰落信道条件下，采用16重分集、32阶正交调制、Turbo/LDPC迭代译码，编码码率为2/3、编码信息长度为384的设计方案，信噪比门限低至3 dB，实现了弱信号高可靠通信。

本研究采用基于分集的非相干多进制正交调制迭代译码，实现了低速率无线通信系统的低信噪比门限传输，但相比通信工程中的香农定理极限，仍存在一定差距，后续可将非相干检测与软判决译码联合进行系统级反馈迭代，进一步改善接收信噪比门限。

参考文献/References：

[1] KHAN M J，AZIM A W，GUENNEC Y L，et al.Theoretical and experimental analysis of asymmetrically Clipped-FSK VLC system[J].IEEE Photonics Journal，2022，14（3）：1-9.

［2］ BELLILI F，SELMI Y，AFFES S，et al.A Low-cost and robust maximum likelihood joint estimator for the doppler spread and CFO parameters over flat-fading rayleigh channels［J］.IEEE Transactions on Communications，2017，65（8）：3467-3478.

［3］ SWATHIKA R，KUMAR S M D.Analysis of BER perfor-mance over AWGN and rayleigh channels using FSK and PSK modulation schemes in LoRa based IoT networks［C］//2023 International Conference on Intelligent and Innovative Technologies in Computing，Electrical and Electronics （IITCEE）.Bengaluru：IEEE，2023：351-357.

［4］ 刘永桦，王鹏毅，王西夺.一种低信噪比突发信号载波跟踪技术研究［J］.河北工业科技，2021，38（1）：12-19.

LIU Yonghua，WANG Pengyi，WANG Xiduo.Research on technology of carrier tracking for burst signals with low SNR［J］.Hebei Journal of Industrial Science and Technology，2021，38（1）：12-19.

［5］ FU Hua，KAM P Y.Effect of doppler shift on performance of binary DPSK over fast Rician fading channels with diversity reception［C］//2008 International Symposium on Information Theory and Its Applications.Auckland：IEEE，2008：1-6.

［6］ 李可，孙志国，宁晓燕，等.正交调制通信系统对多普勒频移响应分析［J］.哈尔滨工程大学学报，2019，40（7）：1361-1366.

LI Ke，SUN Zhiguo，NING Xiaoyan，et al.Analysis of doppler frequency shift response in orthogonal modulation communication system［J］.Journal of Harbin Engineering University，2019，40（7）：1361-1366.

［7］ 孙柏昶，陈超群.MFSK调制方式在极低速通信中的性能分析［J］.无线电通信技术，2019，45（2）：182-185.

SUN Baichang，CHEN Chaoqun.Performance analysis of MFSK modulation in ultra-low speed communication［J］.Radio Communications Technology，2019，45（2）：182-185.

［8］ 邢亚斌，王振岭，杨再秀.基于FFT的突发扩频信号兼容快捕算法［J］.河北工业科技，2017，34（6）：395-401.

XING Yabin，WANG Zhenling，YANG Zaixiu.Compatible fast acquisition algorithm for burst spread spectrum signal based on FFT［J］.Hebei Journal of Industrial Science and Technology，2017，34（6）：395-401.

［9］ 于茜，罗永健.耦合混沌系统的自适应同步及其在保密通信中的应用［J］.河北科技大学学报，2011，32（2）：157-161.

YU Qian，LUO Yongjian.Adaptive synchronization of coupled system and its application to secure communication［J］.Journal of Hebei University of Science and Technology，2011，32（2）：157-161.

［10］徐信.JTIDS系统的多进制扩频检测方法和软输出算法［J］.无线电通信技术，2013，39（5）：37-40.

XU Xin.Detection methods and soft-output algorithms for M-ary spread modulation in JTIDS［J］.Radio Communications Technology，2013，39（5）：37-40.

［11］MIQUEU P，KHAN M J，GUENNEC Y L，et al.Turbo-DC-FSK： Joint turbo coding and FSK-based modulation for visible light communications［C］//2022 Joint European Conference on Networks and Communications & 6G Summit （EuCNC/6G Summit）.Grenoble：IEEE，2022：25-30.

［12］陈文龙.高动态多进制扩频系统的关键技术研究［D］.西安：西安电子科技大学，2009.

CHEN Wenlong.Research on Key Techniques for the M-ary Spread Spectrum System in High Dynamic Situation［D］.Xi′an：Xidian University，2009.

［13］CHOI J D，YOO D S，STARK W E.Performance limits of M-FSK with reed-solomon coding and diversity combining［J］.IEEE Transactions on Communications，2002，50（11）：1787-1797.

［14］VANGELISTA L.Frequency shift chirp modulation： The LoRa modulation［J］.IEEE Signal Processing Letters，2017，24（12）：1818-1821.

［15］VALENTI M C，CHENG Shi.Iterative demodulation and decoding of turbo-coded M-ary noncoherent orthogonal modulation［J］.IEEE Journal on Selected Areas in Communications，2005，23（9）：1739-1747.

［16］白宝明，孙韶辉，王加庆.5G移动通信中的信道编码［M］.北京：电子工业出版社，2020：82-88.

［17］RAMESH A，CHOCKALINGAM A，MILSTEIN L B.Performance of noncoherent turbo detection on Rayleigh fading channels［C］//GLOBECOM′01. IEEE Global Telecommunications Conference （Cat. No.01CH37270）.San Antonio：IEEE，2001：1193-1198.

［18］FABREGAS A G I，GRANT A J.Capacity approaching codes for non-coherent orthogonal modulation［J］.IEEE Transactions on Wireless Communications，2007，6（11）：4004-4013.

［19］PROAKIS J G.数字通信［M］.2版.北京：电子工业出版社，2003：598-602.

［20］SHIRVANIMOGHADDAM M，LI Yonghui，VUCETIC B.Near-capacity adaptive analog fountain codes for wireless channels［J］.IEEE Communications Letters，2013，17（12）：2241-2244.

［21］张玉明，程云鹏，魏胜群，等.双多进制正交扩频系统的比特软值输出算法［J］.电子与信息学报，2006，28（3）：455-460.

ZHANG Yuming，CHENG Yunpeng，WEI Shengqun，et al.Bit soft-output algorithm for dual N-ary orthogonal spread spectrum system［J］.Journal of Electronics & Information Technology，2006，28（3）：455-460.