基于EI-D-R模型的降雨型滑坡气象预警研究

摘 要：通过选取平武县的降雨型滑坡为研究对象，统计分析降雨特征，建立EI-D（前期有效降雨强度—历时）阈值模型，并在此基础上建立EI-D-R（前期有效降雨强度—历时—当日降雨强度）阈值模型。对比分析两种阈值模型的预警精度。结果表明：相较于EI-D模型，EI-D-R模型在高危险预警区与极高危险预警区分别提升了6%和13%；而在当日降雨量＞25 mm的EI-D模型中有11%的滑坡事件由中危险预警区升至EI-D-R模型的高危险预警区，EI-D模型中有11%的滑坡事件由高危险预警区提升至EI-D-R模型的极高危险预警区，减少了当日降雨强度与前期降雨量过大引起的误差。

关键词：降雨型滑坡；降雨阈值；EI-D-R模型；平武县

中图分类号：P642.22 文献标志码：B 文章编号：2095–3305（2024）07–0-03

滑坡灾害在世界范围内屡见不鲜，对人们的生命安全和财产生活构成很大的威胁[1]。在山区，降雨频率高，容易引起地质灾害，因此预防滑坡显得十分重要[2]。当前，降雨滑坡预警模型可分为两大类：一类是基于物理方法和数学方法的模型，其使用大量土壤岩性、降雨量、植被根系等参数确定降雨阈值，该方法确定的降雨阈值较为准确，但受到模型建立复杂、数据所需精度高、计算量大等特点的限制，对部分特殊的滑坡有很好的预警效果，不适合在区域的降雨预警中使用。另一类是基于数学统计模型，不考虑降雨量和滑坡区域等的差异，将历史降雨量与滑坡相结合，建立宏观降雨与滑坡间的预警关系[3]。1980年，Caine[4]统计降雨历时与降雨强度，提出了降雨强度—历时阈值（I-D阈值曲线）。由于降雨型滑坡的发生是一个降雨累积过程，其中降雨量会因许多作用而减少，因此使用前期有效降雨量更符合实际情况。当极端天气发生滑坡，前期降雨量与当日降雨量的差异较大，刘谢攀等[5]引入当日降雨强度R，建立I-D-R（前期有效降雨强度—降雨历时—当日降雨强度）模型，构建更加精确的模型。

1 研究区概况

平武县位于四川盆地西北部，地处103°～104°E，31°～33°N，位于涪江上游，具有典型的山地地貌景观，属亚热带季风气候，雨量丰富[6]。研究区内不同季节间降雨差异明显，受地理环境影响，降雨量呈季节性变化，7—8月降雨量最大。据2008—2021年统计，共发生滑坡1 423例，降雨是影响滑坡的主要因素，占比为67.3%。

2 前期有效降雨量计算

斜坡在降雨条件下发生滑动，主要受以下2种因素影响：一是前期降雨使坡体结构朝着劣化的方向发展；二是当日降雨使滑坡产生变形、位移等现象。以下主要介绍前期降雨量相关计算。

2.1 前期降雨时间范围的选取

69a2dc2e2c1246f7b609598bd731afb5

由于降雨促使斜坡失稳是一个长期的过程，因此前期降雨时间范围是一个重要条件。采用二元逻辑回归模型，得到需要考虑的前期降雨时间范围，将滑坡发生取值为1，不发生取值为0。将所收集的降雨资料通过软件建立二元逻辑回归模型。得到结果见表1。

由表1可知，前1～3日的回归系数B都为正值，前4日为负值，说明随着降雨量的增加滑坡发生可能性反而减小，说明滑坡前3日的降雨对滑坡影响较大，因此前期降雨时间范围取值为3 d。

2.2 有效降雨系数

在多数降雨型滑坡中，前期降雨对滑坡的产生是不可忽视的，但当降雨至地面到形成滑坡的过程中，雨水会随着时间推移发生蒸发、地表径流等作用。只有部分地表水进入岩土体，增大了岩土体孔隙水压力，使处于极限平衡状态的斜坡产生滑动。使用Crozier提出的前期有效降雨量计算方法。具体如下：

Re=R0+αR1+α2R2+，…，+αnRn（1）

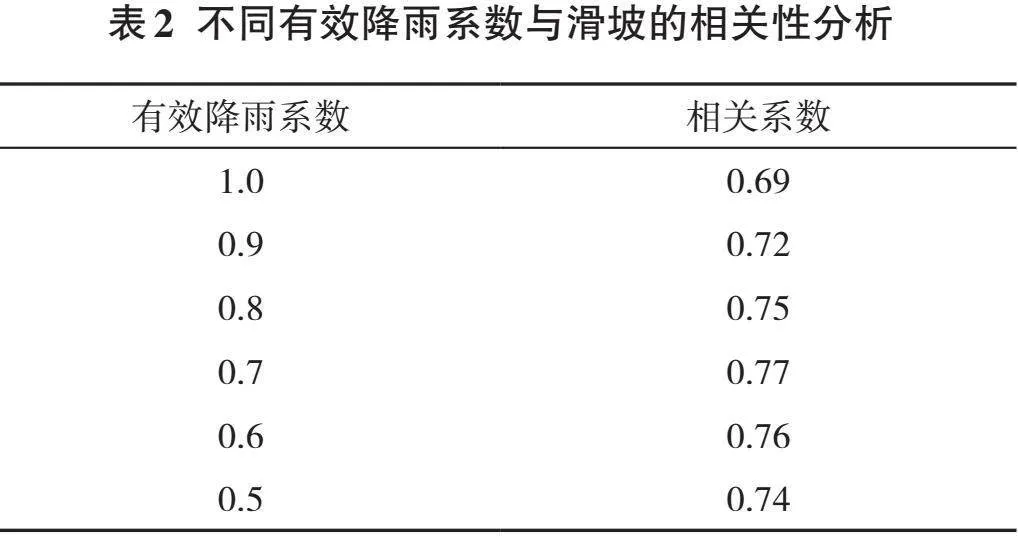
式（1）中，Re为前期有效降雨量，Rn为前n日降雨量，α为有效降雨系数。采用相关性分析法，计算不同有效降雨系数与滑坡发生次数之间的相关系数（表2）。相关系数且先增大后减小，在有效降雨系数为0.7时两者相关性最高，因此，α=0.7。

3 滑坡降雨阈值模型

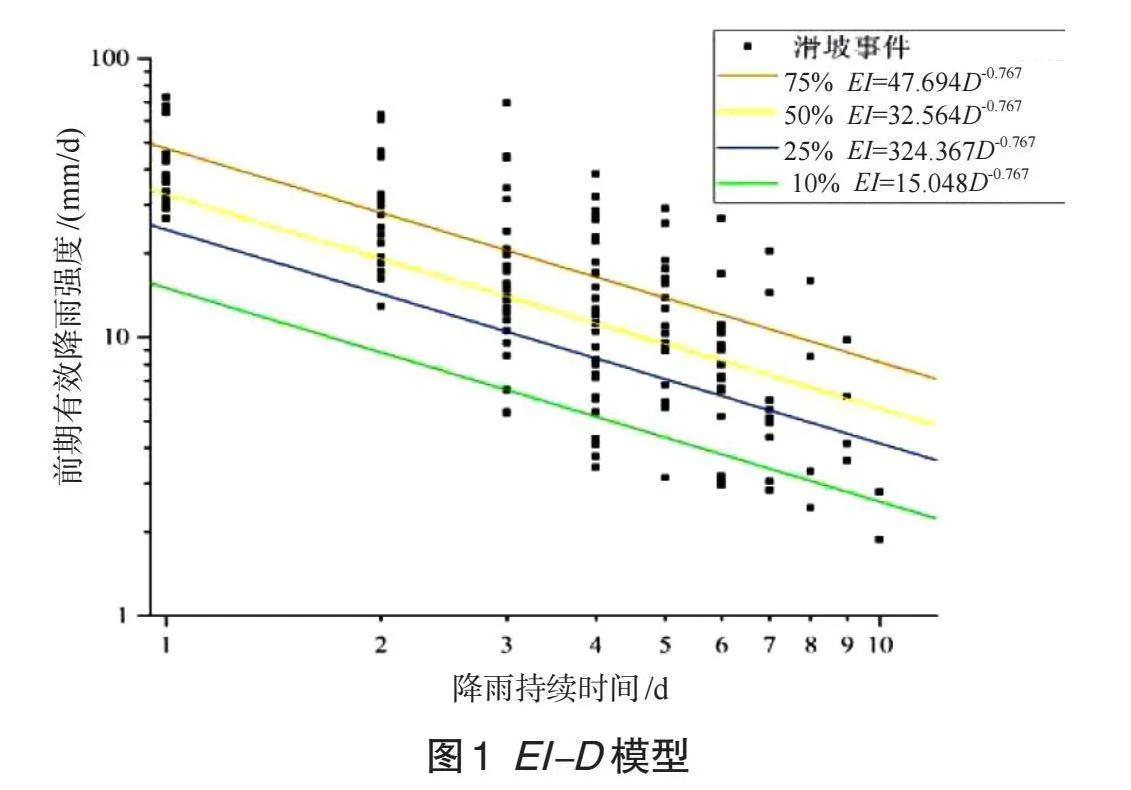
建立的EI-D降雨阈值模型是指在设定的滑坡发生概率下，描述不同概率下降雨型滑坡发生的前期有效降雨强度EI与降雨持续时间D关系曲线。其表达式如下：

EI=c+βDγ（2）

式（2）中，EI为前期有效降雨强度，D为降雨持续时间，β和γ为统计参数，c≥0。

为明确平武县滑坡的降雨特征，将同一天产生的滑坡作为一个滑坡事件，因此将上述的滑坡分为159例滑坡事件[7]。有研究表明，随着时间的拉长，前期有效降雨强度与当日降雨量差异增大，造成滑坡预警等级的误报，因此进行降雨型滑坡预警时需要将当日降雨量作为重要影响因素，在EI-D模型的基础上考虑当日降雨强度R，可以提高模型精度[8]。其表达式为：

EI=c+αDβRγ（3）

式（3）中，α、β、γ为统计参数，c≥0。

4 研究成果

4.1 EI-D阈值模型

通过分析滑坡事件的前期有效降雨强度和降雨持

续时间的关系，根据滑坡发生的概率进行拟合得到降雨阈值。最终对滑坡事件进行散点拟合，按危险程度分为5个不同的滑坡危险预警区：极低危险预警区（＜10%）、低危险预警区（10%～25%）、中危险预警区（25%～50%）、高危险预警区（50%～75%）、极高危险预警区（＞75%），随机选择其中15例滑坡事件作为验证。不同的降雨阈值曲线分别为EI10%=15.1D-0.7、EI25%

=24.3D-0.7、EI50%=32.5D-0.7、EI75%=47.6D-0.7。其关系如图1所示。

4.2 EI-D-R阈值模型

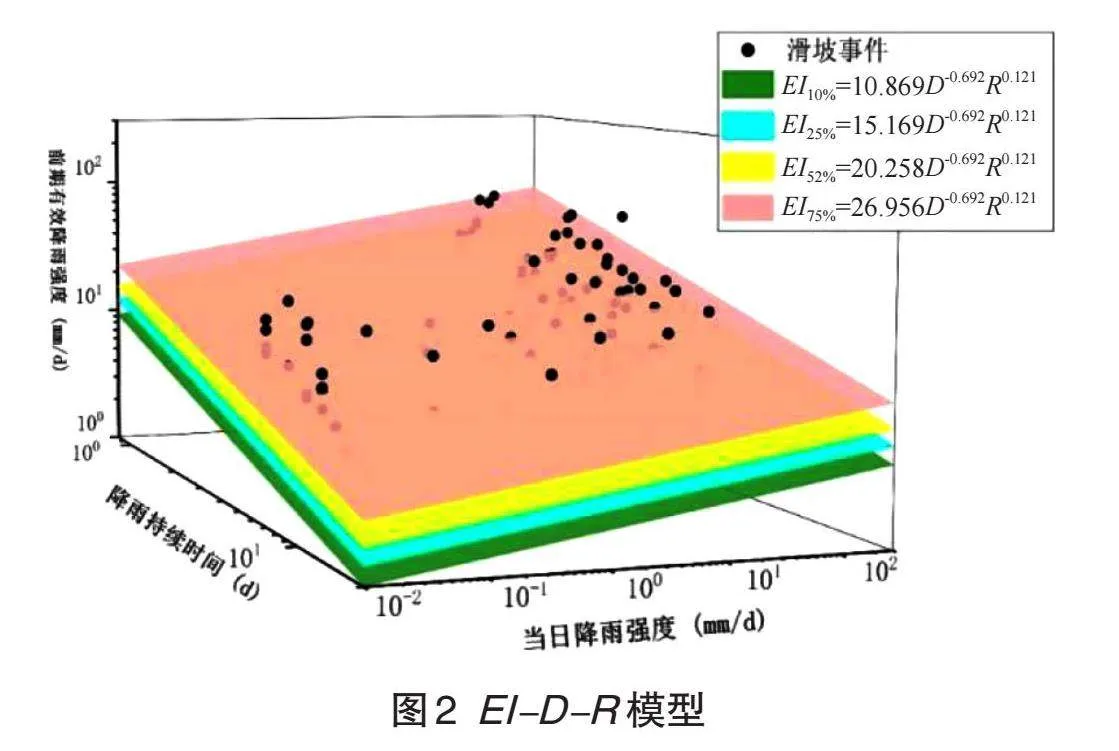
以相同的滑坡事件建立EI-D-R模型。该模型在EI-D模型的基础上引入了当日降雨强度R，确保模型准确性。模型以3对数坐标系表示前期有效降雨强度—降雨持续时间—当日降雨强度的关系，以相同的标准划分5个不同滑坡危险预警区。其关系结构如图2所示。

通过对不同滑坡事件进行拟合，滑坡事件的危险性分级与EI-D划分等级相同，各个等级的降雨阈值曲面分别为EI10%=10.8D-0.6R0.1、EI25%=15.1D-0.6R0.1、EI50%=20.2D-0.6R0.1、EI75%=26.9D-0.6R0.1。

4.3 精度对比

将未参与实验的15例滑坡事件对2个模型进行精度验证（表3），在EI-D模型中有14%的滑坡处于极低危险预警区，26%位于中危险预警区，47%位于高危险预警区，13%位于极高危险预警区。在EI-D-R模型中，有7%的滑坡位于极低风险预警区，有7%的滑坡位于低风险预警区，有7%的滑坡位于中危险预警区，53%位于高危险预警区，26%位于极高危险预警区。

由表3可知，EI-D模型在进行不同等级的危险预警区等级划分时更趋向于平均水平，无法体现极端情况下产生的滑坡。而EI-D-R模型将原本的二维划分变为三维划分，能体现极端天气下降雨对滑坡的影响，EI-D-R模型在极端条件下的预警精度更高。共有60%的滑坡事件当日降雨量＞25 mm（大雨），EI-D模型中有11%的滑坡事件由中危险预警区提升至EI-D-R模型的高危险预警区，EI-D模型中有11%的滑坡事件由高危险预警区提升至EI-D-R模型的极高危险预警区。

5 结论

区域型降雨预警模型的建立主要通过历史降雨信息和有记录的滑坡案例，从降雨的雨量、雨强、历时等建立与滑坡的关系。EI-D-R模型相较于EI-D模型考虑了当日降雨强度R，将二维划分变为三维划分，将降雨阈值曲线也变为降雨阈值曲面，更能体现极端天气下降雨对滑坡的影响，得到以下结论。

（1）平武县滑坡与降雨关系显著，对滑坡事件与降雨量进行回归分析可知，平武县降雨型滑坡在第3天与累计降雨量相关性最强。考虑到降雨会产生蒸发、入渗等作用，其衰减系数为0.7。

（2）在EI-D模型基础上引入当日降雨量，建立三维降雨阈值模型不同概率的EI10%=10.8D-0.6R0.1、EI25%=15.1D-0.6R0.1、EI50%=20.2D-0.6R0.1、EI75%=26.9D-0.6R0.1。通过精度验证发现，EI-D模型中有11%的滑坡事件由中危险预警区提升至EI-D-R模型的高危险预警区，EI-D模型中有11%的滑坡事件由高危险预警区提升至EI-D-R模型的极高危险预警区，减少了当日降雨强度与前期降雨量过大引起的误差。

参考文献

[1] 陈洪凯，魏来，谭玲.降雨型滑坡经验性降雨阈值研究综述[J].重庆交通大学学报（自然科学版），2012，31（5）：990-996.

[2] 范江琳，郭晓军，青泉，等.基于降雨分级的泥石流降雨I-D预报模型[J].气象科技，2020，48（2）：242-247.

[3] 杨诗诗，叶润青，付小林，等.三峡库区降雨型滑坡预警雨量阈值研究[J].华南地质，2023，39（3）：445-454.

[4] Caine N. The Rainfall Intensity： Duration Control of Shallow Landslides and Debris Flows[J]. Geografiska Annaler Series A-physical Geography， 1980， 62（1/2）： 23-27.

[5] 刘谢攀，殷坤龙，肖常贵，等.基于I-D-R阈值模型的滑坡气象预警[J].地球科学，2024，49（3）：1039-1051.

[6] 张文，白世彪，王建.基于专家经验值的滑坡易发性评价：以四川平武高坪铺库区为例[J].地质灾害与环境保护， 2010，21（4）：20/23，37.

[7] 张勇，温智，程英建.四川巴中市滑坡灾害与降雨雨型关系探讨[J].水文地质工程地质，2020，47（2）：178-182.

[8] 林巍，李远耀，徐勇，等.湖南慈利县滑坡灾害的临界降雨量阈值研究[J].长江科学院院报，2020，37（2）：48-54.