蒙特卡洛树搜索实验设计

摘要：蒙特卡洛树搜索是实现智能博弈程序的关键技术，是人工智能课程的重要内容。本文面向人工智能课程实践教学，针对现有教材偏重理论介绍缺乏实践引导的问题，设计了以黑白棋为例的蒙特卡洛树搜索实验，帮助学生理解蒙特卡洛树搜索的主要流程与设计原理。本文首先运用图解方式直观展示蒙特卡洛树的创建与扩展过程；其次引入算法的模块化实现方法；最后，将蒙特卡洛树搜索应用于智能黑白棋程序设计，通过图形界面展示搜索结果，实现交互式人机对弈。教学实践表明，通过动手实现基于蒙特卡洛树搜索的智能黑白棋程序，能够加深学生对算法的理解，提升学生创新实践能力。

关键词：人工智能；蒙特卡洛树搜索；黑白棋；AlphaGo

中图分类号：TP391.4

蒙特卡洛树搜索（MonteCarloTreeSearch，MCTS）是一种用于决策过程的搜索算法，其基本目标是给定问题的一个状态，选择该状态下一个最优的行动方案。蒙特卡洛书搜索结合了随机模拟和树搜索的优点，通过模拟来评估不同的状态的优劣，从而找到最优的行动方案。蒙特卡洛树搜索于2006年被提出［1］，初始应用于围棋游戏。随后，谷歌公司DeepMind团队将其与深度学习技术结合，开发了智能系统AlphaGo［2］，战胜了顶尖职业围棋选手，成为人工智能领域里程碑事件之一。蒙特卡洛树搜索是一个应用非常广泛的博弈算法，除了用于双人零和博弈问题（例如围棋、象棋），也应用于路径规划等重要任务［3］。

蒙特卡洛树搜索是人工智能课程的重要内容，对学生掌握智能程序设计方法具有十分重要的作用［4-6］。然而，现有的大部分人工智能教材依然将早期的博弈搜索技术（极小极大搜索）作为课程的教学重点，缺乏对蒙特卡洛树搜索等新型博弈搜索技术的讲解。部分教材即使涉及蒙特卡洛树搜索，也只是蜻蜓点水，对算法原理的描述不够详细，同时缺乏教学案例与实验案例支撑。本文的主要目的是实现人工智能课程博弈搜索知识点的教学重点从早期的极小极大搜索到目前主流的蒙特卡洛树搜索的转移，随时代发展更新人工智能课程教学内容，探讨如何设计可视化的蒙特卡洛树搜索实验，促进学生对算法的理解，提升智能程序设计水平，提升实践教学效果。

本文的主要内容和结构安排如下：第1节主要介绍蒙特卡洛树搜索的基本流程与原理；第2节设计基于黑白棋的蒙特卡洛树搜索实验；第3节对实验结果进行展示；第4节对本文进行总结。

1蒙特卡洛树搜索理论基础

1997年，IBM公司设计的深蓝程序战胜当时的国际象棋世界冠军加里·卡斯帕洛夫，成为计算机智能博弈程序的标志性事件之一。深蓝用到的主要技术包括极小极大搜索，每秒能够探查2亿个位置，使用了非常复杂的评估函数和一些未公开的方法将某些搜索分支延伸至40层［7］。自此之后，极小极大搜索成为人工智能课程博弈搜索部分的重要知识点。极小极大搜索是基于博弈树的搜索算法，它使用博弈树表示一个游戏。博弈树中每个结点都代表一个状态，根结e5c1d78284320fe2a70c5d099b4908963712c82cd7db9063336cda788aeebe2c点表示初始状态，叶子结点表示终止状态。从一个结点移动一步，将会到达它的子结点，一个结点包含子结点的数目称为分支因子。极小极大搜索并未显式构造整棵博弈树，而是通过递归的方式计算根结点的每个子结点的收益，从而选择最佳行动方案。对于具有很大分支因子的游戏，博弈树非常巨大，无法有效进行搜索。此时，极小极大搜索需要限定搜索深度。我们无法保证在指定深度处的结点都是终止结点，因此需要一个函数来评估非终止状态的局势。然而，评估函数设计非常困难，通常需要借助领域专家经验。

与极小极大搜索相同，蒙特卡洛树搜索也是基于博弈树的搜索算法，不同点在于蒙特卡洛树搜索显式存储博弈树。蒙特卡洛树搜索采用迭代构建的思想，从单个根结点开始，不断扩充博弈树，直至用完限定的搜索时间，再根据构建的博弈树制订当前最佳的行动方案。对于非叶子结点，蒙特卡洛树搜索不依赖于评估函数计算结点收益，而是通过多次模拟博弈，根据模拟结果估算结点收益。以围棋为例，在某个特定盘面s情况下，进行n次对局，如果统计出黑棋赢得多，说明盘面s对黑棋比较有利。通过模拟对弈的方式评估结点收益，计算量大，评估次数有限。因此，蒙特卡洛树搜索提供了一种选择机制，尽量选择博弈树中比较有潜力的结点进行模拟，从而使得博弈树在“较好”的策略上“生长”。

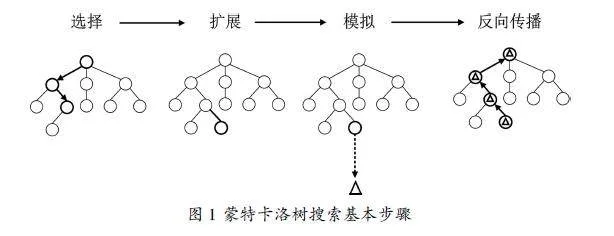
蒙特卡洛树搜索每一轮迭代都是从根结点出发，顺序执行“选择”—“扩展”—“模拟”—“反向传播”四个步骤，不断扩充博弈树。图1展示了蒙特卡洛树搜索一轮迭代的执行示例，接下来详细介绍每一个步骤。

1.1选择

从根结点出发，自上而下迭代执行子结点选择策略，直至到达一个可扩展的结点。一个结点是可扩展的，当且仅当其所包含的状态是非终止状态，且还有未扩展的子结点。选择策略的基本思想是让博弈树向最优的方向扩展，也就是要选择一个尽量“有潜力”的树结点。有潜力的结点可以由两方面因素进行评估，一个是胜率高，另一个是被考察的次数少。胜率高的结点意味着最后赢棋的概率较大，应该多花精力分析其后续走法。被考察次数少意味着该结点尚未经过充分研究，有成为黑马的可能。下表综合两个方面的因素总结了结点的潜力。

假设当前所在树结点为S0，S0具有b个子结点，分别记为S1，S2，…，Sb。蒙特卡洛树通常用上置信区间（UpperConfidenceBound，UCB）公式对每个子结点的潜力进行量化评估，从而计算结点的“潜力”。第i个子结点Si的“潜力”具体计算公式如下：

UCB（Si）=tini+clnNni

其中，ti表示从子结点Si所含状态出发后续取胜的次数（或者收益），ni表示结点Si的访问次数，c是一个维护探索与利用平衡的参数，在实际应用中凭经验进行选择，N表示当前结点S0的访问次数，等于所有ni之和。公式等号右侧第一项代表了结点的胜率指标，第二项代表了结点的访问次数指标，参数c数值越大，扩展过程越照顾访问次数较少的结点。

1.2扩展

根据当前可执行的行动（可能的落子方法），向选定的结点上添加一个子结点扩展搜索树，同时选择该子结点。

1.3模拟

以新扩展的子结点作为模拟的根结点开始模拟博弈，不断地交替随机落子直至棋局结束，并根据结束时的胜负状态来确定结点的收益，这一步骤又称为Rollout。Rollout过程中采用的走子策略执行速度需要足够快，以便仿真能够快速完成，这样才能得到尽量多的仿真结果，使统计结果逼近真实的胜率。蒙特卡洛树搜索一般采用随机策略，实际应用中也可以采用一些“有经验”的策略，或者两者的结合。所谓有经验的策略就像一个有一定水平的棋手，可以下出一些比较好的走法。此外，我们可以在仿真的某个阶段采用棋手的走法，另外一些阶段采用随机走法。

1.4反向传播

模拟完成之后，需要将模拟结果反向传播回当前博弈树的根结点，更新从模拟结点到根结点的路径上的结点信息。更新的结点信息包含两个部分，一个是结点访问次数，另一个是结点收益。

1.5制订行动方案

蒙特卡洛树搜索终止条件一般设定为到达指定的运行时间。当给定时间用完时，算法终止。搜索结束时，我们需要根据构建出的博弈树选择行动方案。以根结点为基，选择行动方案的方式有三种：（1）选择具有最大收益的子结点；（2）选择具有最多访问次数的子结点；（3）选择最大化UCB数值的子结点。

1.6蒙特卡洛树搜索的优缺点

相较于极小极大搜索，蒙特卡洛树搜索的优点包括：（1）无须设计评估函数，不要求设计者具有问题领域相关的知识，可以在只知道博弈游戏规则的情况下进行搜索，可以应用于不同的博弈问题，是一种通用方法；（2）博弈树构建是一种非对称扩展过程，选择策略会更频繁地访问更有希望取胜的结点，并聚焦搜索时间在这些结点上，避免大的分支因子带来的搜索空间爆炸问题；（3）算法任意时间可输出，搜索可以在任何时间终止，并返回当前估计的最佳走棋，构造出来的搜索树可供后续搜索重用。蒙特卡洛树搜索的主要缺点是需要足够多的迭代才能收敛到一个很好的行动方案上，例如针对围棋可能需要百万次的模拟交战才能得到专家级的行动方案。

2基于蒙特卡洛树搜索的智能黑白棋程序

2.1实验设计的主要目的

蒙特卡洛树搜索的流程较为复杂，仅通过课堂讲解难以令学生对算法流程具有深刻认识，因此需要辅助实验。通过编码实现算法的每一个步骤，可以加深对算法的理解。一种实验方式是将完整算法代码提供给学生，学生参照代码复现一次，这种方式缺乏挑战度，难以激发学生学习兴趣。另一种方式是从零构建代码框架，实现每一个步骤，这种方式的缺点是难度过大，学生容易将精力花费在图形界面编程而不是算法核心步骤上。因此，实验采用一种折中的方式，为学生提供完整的代码框架，将核心函数挖空，要求学生在充分理解算法步骤的前提下完善挖空的核心函数。学生不用分心于如何实现博弈游戏的图形界面，可以将精力集中在算法核心步骤的实现，提升教学效果。

2.2智能黑白棋程序

实验将蒙特卡洛树搜索应用于黑白棋游戏，选择黑白棋的主要原因包含两个方面：（1）黑白棋游戏规则简单，容易上手，即使从未接触过棋类游戏也可以在几分钟内掌握，适应学生学情；（2）黑白棋棋盘为8×8的网格，对应的博弈树规模适中，既不会太小使得可以通过极小极大搜索遍历整棵博弈树，也不会太大导致需要百万次模拟才能得到较好的行动方案。学生可以在个人计算机上运行蒙特卡洛树搜索获得不错的智能黑白棋程序，完成实验的时间可以灵活设置。

2.3代码模块

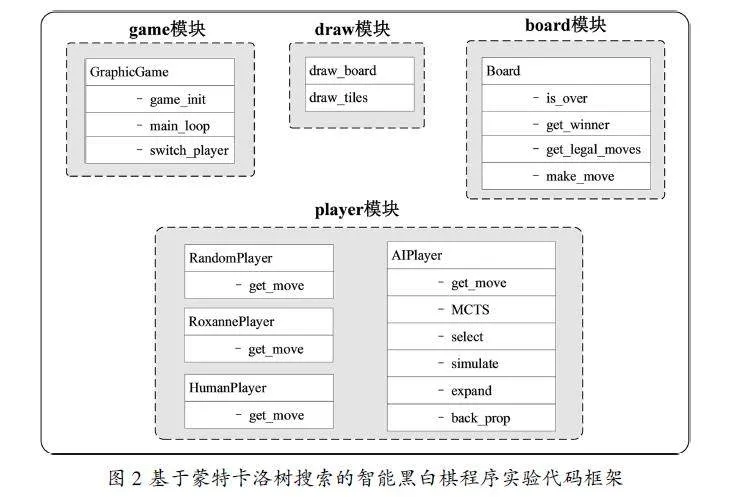
实验提供了智能黑白棋程序的主体框架，框架使用Python语言实现。图2展示了代码整体结构，分为game、draw、board和player四个模块。下面是四个模块的简单介绍。

（1）game模块是主程序模块，实现了GraphicGame类，负责参数初始化与基本逻辑控制，包含主循环。

（2）draw模块负责图形界面绘制，包含了绘制棋盘与棋子的函数。

（3）board模块包含了棋盘类Board，负责记录棋盘信息以及进行游戏规则判定，包含is_over、get_winner、get_legal_moves以及make_move方法，分别用于判断棋局是否结束、胜者是哪一方、获取当前玩家合法落子位置以及执行落子并更新棋盘。

（4）player模块包含了不同类型的玩家类，分别为随机玩家RandomPlayer、策略玩家RoxannePlayer、人类玩家HumanPlayer以及智能体玩家AIPlayer。玩家类包含一个主要方法get_move，输入一个棋盘类对象，输出在该棋盘局面下采取的行动方案。RandomPlayer在合法位置随机落子，RoxannePlayer依据Roxanne策略选择落子点，HumanPlayer根据鼠标点击位置确定落子点，AIPlayer采用蒙特卡洛树搜索的结果选择落子点。

蒙特卡洛树搜索算法在AIPlayer类中实现，由MCTS、select、expand、simulate与back_prop五个方法共同组成，MCTS方法包含算法迭代主体，调用剩余四个方法。剩余四个方法分别对应蒙特卡洛树搜索的四个基本步骤，即选择、扩展、模拟与反向传播。学生无须对draw、game和board模块进行修改，只须完成player模块中的基于蒙特卡洛树搜索的智能体AIPlayer。这四个方法主体部分为空，学生需要按要求编写完成四个方法，实现过程中可以对UCB公式中的参数c、rollout中使用的落子策略、棋局结束时的收益以及搜索时间进行灵活调整，这些参数的调整留给学生自由探索。学生完成编码后即可运行黑白棋游戏，检验实现效果。

3实验结果与教学反馈

3.1运行结果

进入游戏之后，人类玩家可以选择先手黑棋或后手白棋，电脑玩家自动选择另一方。随机选择上课班级中的一名学生与智能黑白棋程序进行对弈。图3展示了人类玩家先手和后手的最终博弈情况，结果均为AIPlayer胜，说明基于蒙特卡洛树搜索的程序具有较高的智能，能够有效应对分支因子大的复杂博弈游戏。

3.2教学反馈

在课堂上系统讲解蒙特卡洛树搜索的基本步骤及应用场景之后，引入智能黑白棋程序设计实验，要求学生利用已学知识实现基于蒙特卡洛树搜索的智能黑白棋程序。学生在接触实验后，学习兴趣与课堂参与度明显提升，在实验中遇到难题主动寻找解决方案，增强了实践创新能力。调查问卷反馈结果表示，95%的学生认为实验提升了他们对蒙特卡洛树搜索的兴趣，在兴趣驱使下对算法原理与步骤的掌握更为深刻。90%的学生设计出了能够战胜自己的智能黑白棋程序，这一结果体现了基于蒙特卡洛树搜索的智能黑白棋程序设计实验能够提高学生解决实际问题能力。

结语

蒙特卡洛树搜索是当前主流的博弈搜索技术，适用于复杂的分枝因子较大的博弈游戏，具有重要的应用价值。为了推进人工智能教材知识点更新，实现博弈搜索知识重点从极小极大搜索技术到蒙特卡洛树搜索技术的转变，本文详细介绍了蒙特卡洛树搜索的基本步骤，设计了智能黑白棋程序实验。实验为学生提供了基本的程序框架，将算法核心步骤留空，要求学生在深入理解蒙特卡洛树搜索步骤的前提下，根据代码框架提供的信息，完成核心函数的编写。课堂实践结果表明，运用智能黑白棋程序实验可以增强学生的学习兴趣，提升课堂参与度，帮助学生更好地掌握算法原理，进一步激发学生创新实践能力。

参考文献：

［1］CoulomR.EfficientselectivityandbackupoperatorsinMonte-Carlotreesearch［C］//Internationalconferenceoncomputersandgames.Berlin，Heidelberg：SpringerBerlinHeidelberg，2006：72-83.

［2］SilverD，HuangA，MaddisonCJ，etal.MasteringthegameofGowithdeepneuralnetworksandtreesearch［J］.nature，2016，529（7587）：484-489.

［3］BrowneCB，PowleyE，WhitehouseD，etal.Asurveyofmontecarlo treesearchmethods［J］.IEEETransactionsonComputationalIntelligenceandAIingames，2012，4（1）：1-43.

［4］朱福喜.人工智能［M］.3版.北京：清华大学出版社，2017.

［5］吴飞.人工智能导论：模型与算法［M］.北京：高等教育出版社，2020.

［6］S.Russell，P.Norvig.ArtificialIntelligence：AModernApproach（FourthEdition）［M］.London：Pearson，2020.

［7］CampbellM，HoaneJrAJ，HsuF.Deepblue［J］.Artificialintelligence，2002，134（1-2）：57-83.

基金项目：2022年广东省研究生教育创新计划项目“《人工智能》高水平课程及教材建设”（2022SFKC080）；2022年度东莞理工学院质量工程项目“产教融合和多学科交叉背景下人工智能的教学改革与实践”（202202013）；2020年度东莞理工学院质量工程项目“离散数学”（202002063）；2022年度广东省本科高校教学质量与教学改革工程项目“以学生为中心的《离散数学》课程教学改革与实践”

作者简介：张宇辉（1990—），男，广东梅州人，博士，东莞理工学院计算机科学与技术学院讲师，研究方向：群体智能与进化计算；潘晓衡（1983—），男，湖南衡阳人，硕士，东莞理工学院计算机科学与技术学院高级工程师，研究方向：云计算及人工智能。

*通讯作者：李青青（1991—），女，河南平舆人，博士，东莞理工学院计算机科学与技术学院讲师，研究方向：统计学及人工智能。