基于空间视距的林区曲线道路行车舒适性研究

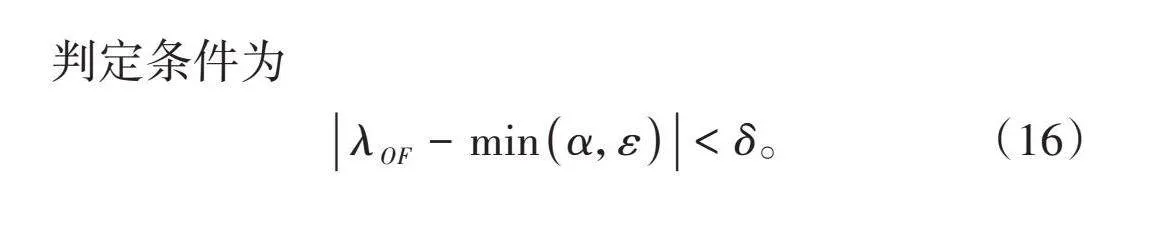
摘 要：为提高林区曲线道路驾驶员行车安全性和舒适性，采用驾驶模拟试验办法，利用眼动和心率作为评价指标，从动态视角对林区曲线道路行车舒适性进行评价研究。基于空间视距理论建立5种不同空间视距的林区曲线道路场景，研究结果表明，驾驶员瞳孔直径变化率和心率增长率随着空间视距增大而不断减小，驾驶舒适性不断增大。考虑瞳孔直径变化率和心率增长率的最小空间视距值为101 m和89 m，得出瞳孔直径变化率和心率增长率的空间视距适宜值为128 m和132 m。

关键词：林区道路； 舒适性评价； 空间视距； 驾驶模拟试验； 驾驶指标

中图分类号：U491.2+1 文献标识码：A DOI：10.7525/j.issn.1006-8023.2024.04.022

Study on Driving Comfort of Curved Roads in Forest Areas Based on Spatial Sight Distance

LI Ankang1， LI Mingbao1*， ZHENG Junjie2

（1.School of Civil Engineering and Transportation， Northeast Forestry University， Harbin 150040， China；2.School of Civil and Hydraulic Engineering， Huazhong University of Science and Technology， Wuhan 430074， China）

Abstract： In order to improve driving safety and comfort of drivers on curved roads in forest areas， a driving simulation test was adopted to evaluate the driving comfort on curved roads in forest areas from a dynamic perspective using eye movement and heart rate as evaluation indexes. Based on the theory of spatial sight distance， five different spatial visual distance scenarios of curved roads in forest areas were established， and the results showed that the rate of change of pupil diameter and the growth rate of heart rate of the driver decreased with the increase of spatial sight distance， and the driving comfort increased continuously. The mi05f95T9WLzNXTFR+QYYarw==nimum spatial sight distance values considering the pupil diameter change rate and heart rate growth rate were 101 m and 89 m， and the appropriate spatial sight distance values considering the pupil diameter change rate and heart rate growth rate were 128 m and 132 m.

Keywords： Forest roads； comfort evaluation； spatial sight distance； driving simulation test； driving indicator

0 引言

近年来，随着我国汽车保有量的增长，道路交通安全问题越来越需要重视。据统计，我国交通事故中弯道区域占交通事故总量的10.5%［1］，其中弯道事故多发，远远高于非弯道路段，特别是林区公路曲线路段。

目前，林区交通事故中与人为因素相关的占到93%［2］，在曲线路段，交通事故率主要与驾驶人视距有关，呈负相关［3］。Chung等［4］研究了道路线形和驾驶疲劳之间的联系。Foy等［5］提出在驾驶过程中驾驶人的心理负荷是关键因素，驾驶员的心理负担随着驾驶环境改变而变化，通过驾驶员的心率变化、眼动变化等直接影响驾驶员操作。郭根盛［6］采用实车试验研究了驾驶员心率增长率和林区公路平曲线半径的关系。王进州等［7］通过实车试验研究驾驶员心率增长率与平曲线转角值的关系。乔建刚等［8］结合驾驶模拟技术探究心率增长率与坡度、平曲线半径、线形组合指标、速度差和交通量之间的关系。潘晓东等［9］通过分析驾驶员心率和血压的变动规律，分析曲线半径的合理性。Wilson［10］运用心电信号来判断驾驶员驾驶过程的心理压力。朱蓉［11］通过驾驶人动视角特性，利用Matlab软件，提出基于B样条曲线三维线形模型的空间动态视距计算办法。孙璐等［12］以可靠度理论为基础，选择曲线半径、路面阻力系数、竖曲线半径作为重要变量，建立基于以上参数的隧道视距可靠性函数。

综上，目前国内外学者在林区道路的研究主要集中在道路线形和驾驶员操作方面，探究驾驶员心率特性、视觉特性与林区道路之间的内在关系。但是关于林区道路行车视距方面较少，行车视距研究主要集中在隧道路段。因此，在现有的研究基础上，运用驾驶模拟试验的办法，分析在不同空间视距下驾驶员行车舒适性，提供适宜的行车视距值。

1 林区曲线道路线形设计方案

1.1 基于行驶稳定考虑的圆曲线最小半径

《林区公路路线设计规范》（LYJ 113—1992）对圆曲线最小半径作了明确规定，其主要是考虑汽车在圆曲线上行驶的稳定性，确保不滑移、不倾覆，但是想要保证车辆在驾驶过程中的稳定性，需要车辆受到的横向力和摩阻力相互抵消，基于行车稳定性的圆曲线半径计算公式为

R=v^2/127（µ_max+i_max ） 。 （1）

式中：R为圆曲线半径，m；v为设计速度，km/h；µ_max为最大横向力系数；imax为最大超高值。

《林区公路工程技术标准》（LY 5104—1998）规定圆曲线部分路段最大超高值在6%，在实际项目设计中，由于地形地貌的影响，驾驶员需要设计较小半径的曲线路段，选择较大的超高值，曲线路段设计时更加游刃有余。综上分析，本研究选择6%作为超高值进行林区曲线路段最小半径的计算。对横向力系数进行选取，表1为我国与其他国家的横向力系数选取。

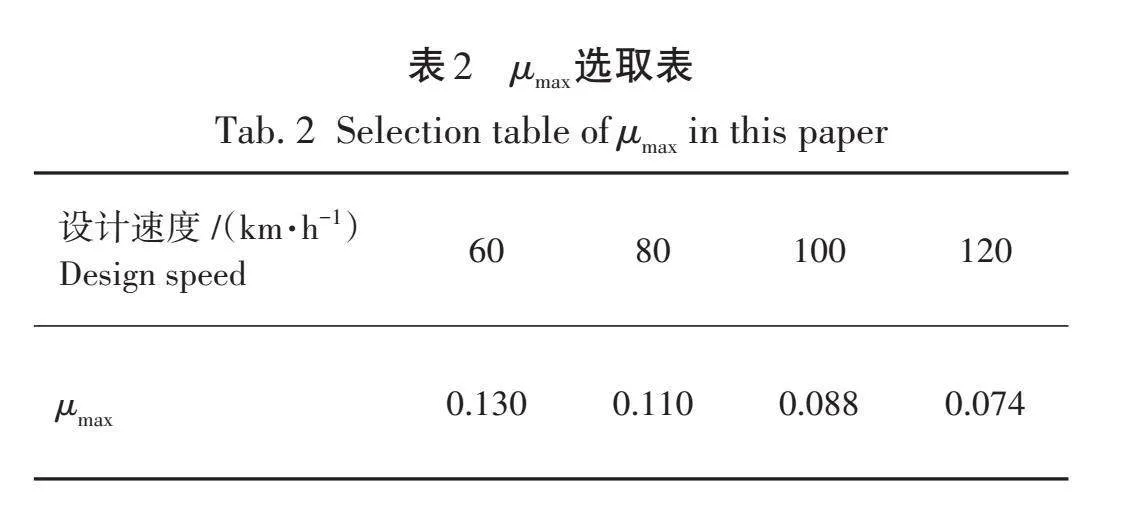
关于最小圆曲线半径的确定，各国的办法基本一致，对µ的取值却各不相同。在µ的选取上，车速较高时选择较小的µ，车速较低时选择较大的µ。本研究在对µ取值时，考虑到增大林区曲线道路圆曲线半径临界最小半径，曲线路段行车安全性更高，驾驶员舒适度更高，因此各工况采用表2中的µmin作为本研究数据，确定圆曲线临界半径的µmax值。

根据公式，以imax=8%、µ=µmax计算满足行车稳定性的圆曲线最小半径，结果见表3。

1.2 基于满足行车视距需求的圆曲线最小半径

根据《林区公路工程技术标准》（LY 5104—1998）规定，驾驶员视点取高于路面1.2 m，林区公路的最小行车视距见表4。

林区曲线路段因为地形地貌的原因和树木遮挡的原因，停车视距如式2所示。

S=S_1+S_2=vt/3.6+v^2/（254（ϕ+ψ））。 （2）

式中：S为停车视距，m；S1为驾驶员反应距离，m；S2为制动距离，m；ϕ为轮胎与路面之间附着系数；ψ为路面摩擦系数；v为行车速度，m/s；t为驾驶员反应时间，s。

同时满足行车视距要求，还要考虑圆曲线半径和横净距大小的影响，横净距是指驾驶员视点轨迹线和视距曲线间的距离，如图1所示。圆曲线内最大横净距，如式（3）所示。

h=R_S-R_S cos r/2=R_S （1-cos r/2）。 （3）

式中：h为最大横净距，m；S为停车视距，m；RS为驾驶员视点轨迹线半径，m；r为视距长度所对的圆心角。

将cos r/2按级数展开，展开式如下。

cos r/2=1-（r/2）^2/2！+（r/2）^4/4！-（r/2）^6/6！+…≈1-（r/2）^2/2！。 （4）

根据式（4）可知

h≈S^2/（8R_S ）。 （5）

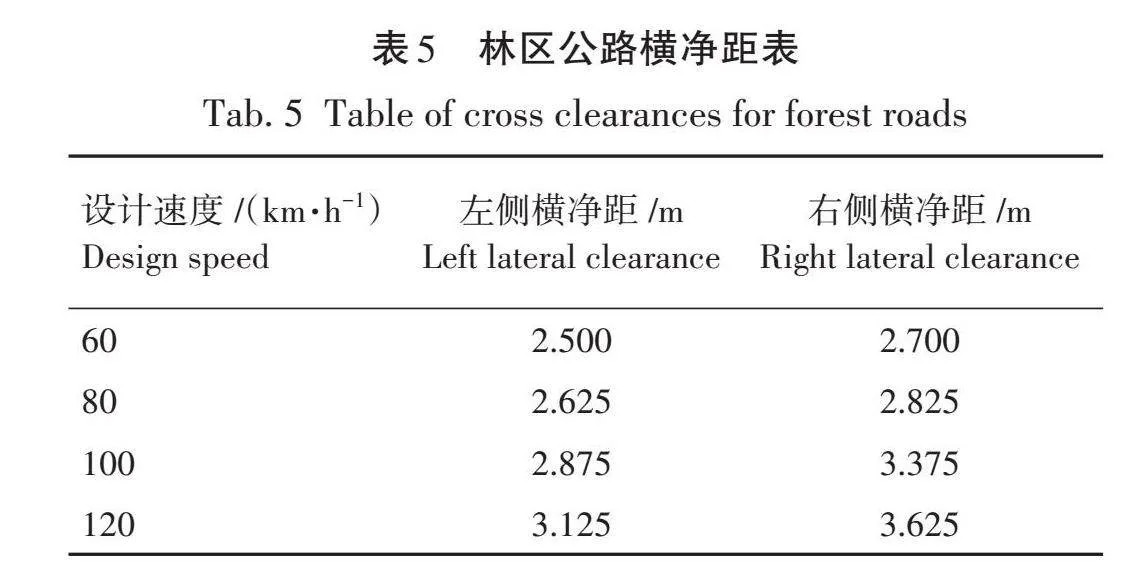
根据《林区公路工程技术标准》（LY 5104—1998）规定，林区公路标准断面见表5。

根据式（5）计算得出结果见表6。

1.3 基于汽车前灯散射角的圆曲线最小半径

在地形地貌复杂的林区公路曲线路段，夜间行车时驾驶人员的视野大小受汽车前灯散射角影响较大，参考赵永平等［13］提出基于汽车前灯散射角的圆曲线最小半径，汽车前灯散射角取α=15°较为合适，停车视距与汽车前灯散射角计算关系如式（6）所示。

S=R πα/180-b。 （6）

式中：S为停车视距，m；R为曲线半径，m；α为汽车前灯计算散角，（°）；b为横净距，m。

计算结果见表7。

1.4 林区曲线道路临界最小半径确定

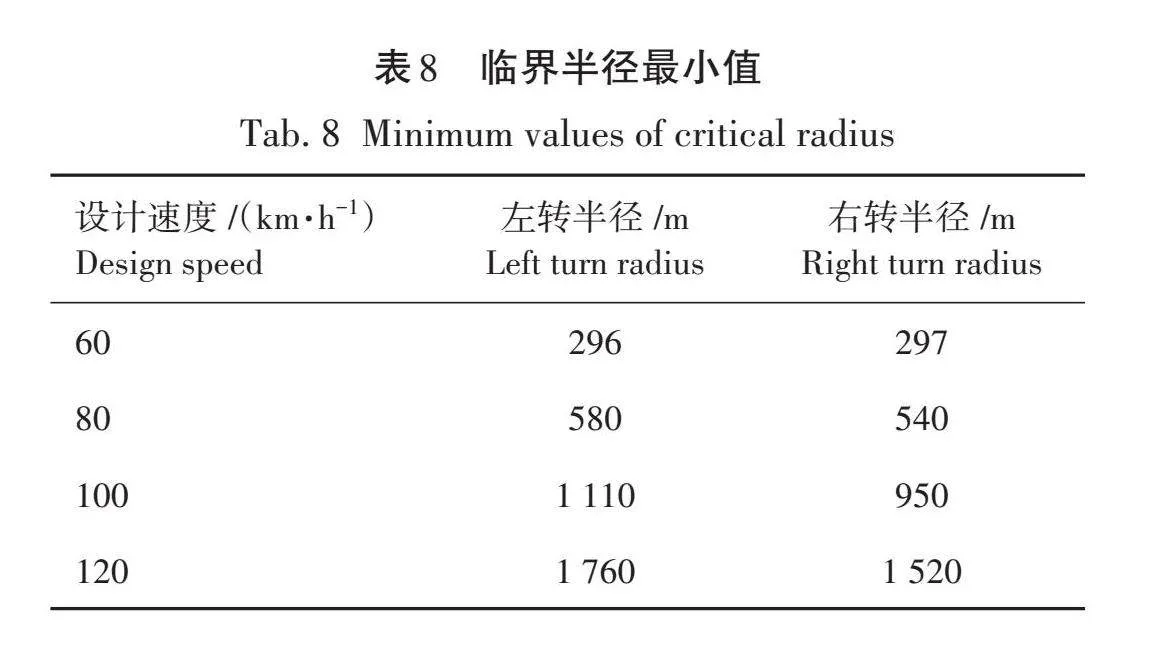
综合以上分析，考虑到林区曲线公路的行车安全，分别考虑行驶稳定性、满足行车视距要求、汽车前灯散射角下各工况曲线半径最大值作为林区曲线道路临界半径最小值，临界半径最小值见表8。

林区公路因为树木遮挡导致视距不足，所以行车速度大多数限制为60 km/h，所以本研究讨论设计速度为60 km/h的林区公路，此时左转临界半径为296 m，右转临界半径为297 m，因此，本研究以200 m为一档，因为本研究主要讨论不同曲线半径路况下实际视距对驾驶行为的影响，所以不考虑左转右转区别。因此，分别建立曲线半径为300、500、700、900、1 100 m的林区曲线道路仿真路况。

2 林区曲线道路三维空间视距确定

2.1 三维空间视距计算原理

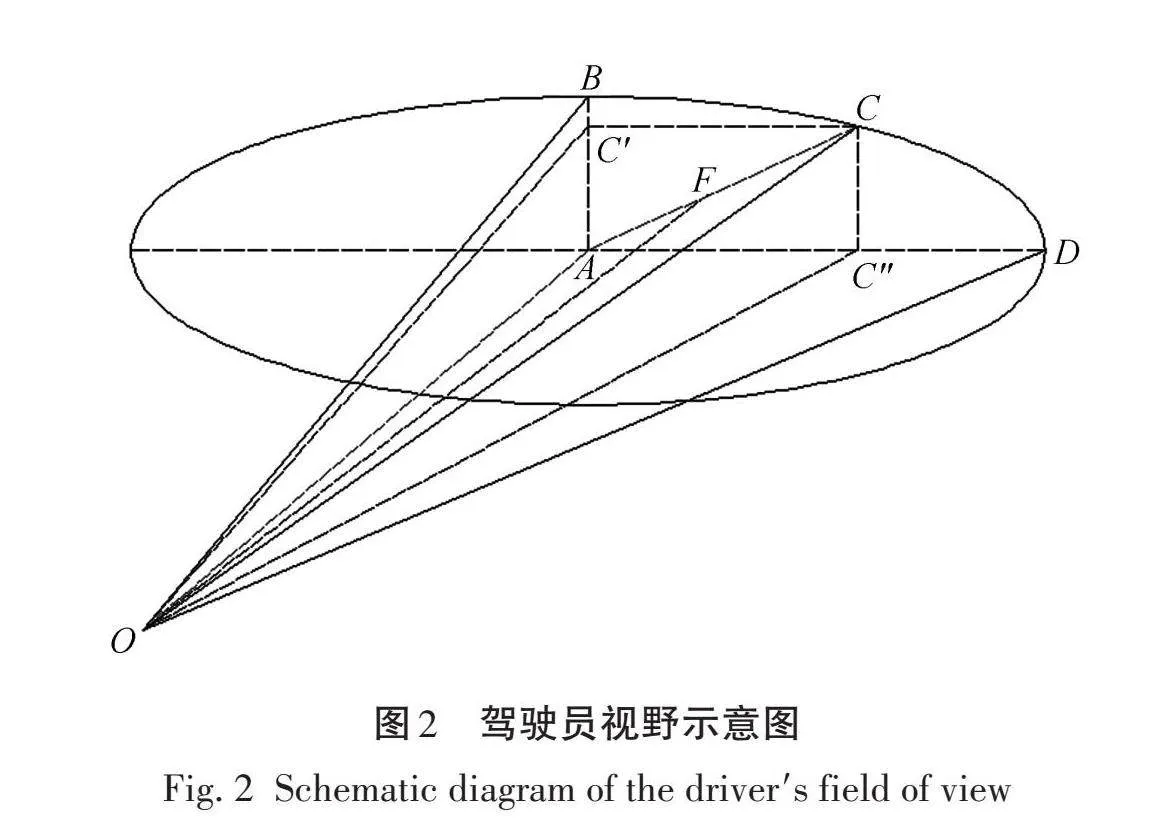
在三维空间中，假设驾驶员的视野呈椭圆锥体，如图2所示。其中，O为驾驶员视线点，B为竖向最远可见视野点，D为横向最远可见视野点，F为沿着车辆行驶方向道路中线上的任一点，C是A点方向驾驶员可见视野最远点。OA为视线中心线，C'和C″为C点在通过视线中心线且与水平面垂直和平行的平面上的投影。∠BOA表示驾驶员能看到竖向最大视野角，记为θ；∠DOA表示驾驶员能看到横向最大视野角，记为α；∠AOC为驾驶员在方向上能够看到的最大视野范围，记为ϕ；∠C′OA为∠AOC在BOA平面内的投影，记为φ。这些元素共同构成了对驾驶员视野的详细几何描述，有助于深入理解驾驶员在不同方向上的视觉感知范围，为交通系统的安全设计提供重要参考［14］。

从驾驶员出发起点开始，对于任一视距计算点O，从车辆行驶方向的第1个驾驶员能看到的点开始进行视距验算，对于视距验算F，通过判断OA和OC的夹角χ是否在O方向最大动态视角ϕ内来确定路线上C点相对于O点的可视性。若O与F间所有点均可视，但下一个验算点不可视，则沿道路中线方向的距离LOF，即为驾驶员在O点的三维动态视距。驾驶员在不受道路周边交通环境影响下能够辨识清楚前方物体的最远距离为Smax，则当视距计算点和验算点距离达到Smax时停止验算，此时该点的动态视距为Smax。

2.2 林区曲线道路三维空间视距空间约束条件

当视距计算点在平纵组合复杂路段时，采取空间约束条件，约束条件如下［14］。

|χ-ϕ|<δ。 （7）

式中，δ为误差限，δ=0.001。

χ=arccos[d_xo （x_F-x_O ）+d_yo （y_F-y_O ）+d_ZO （z_F-z_O ） ]/√（d_xo^2+d_yo^2+d_zo^2×√（（x_F-x_O ）^2+（y_F-y_O ）^2+（z_F-z_O ）^2 ）） 。 （8）

依据空间几何关系，在验算点F驾驶员能观测到的最大视野范围ϕ与∠C′OA为∠AOC在BOA平面内的投影φ的关系为

ϕ=arctan√（tan^2 α-（tan^2 αtan^2 φ）/（tan^2 θ）+tan^2 θ）。 （9）

平面BOA内，投影角φ计算公式为

φ=arccos|（OA） ⃗ |/|（OB） ⃗ | 。 （10）

2.3 林区曲线道路三维空间视距竖向约束条件

2.3.1 凸曲线路段

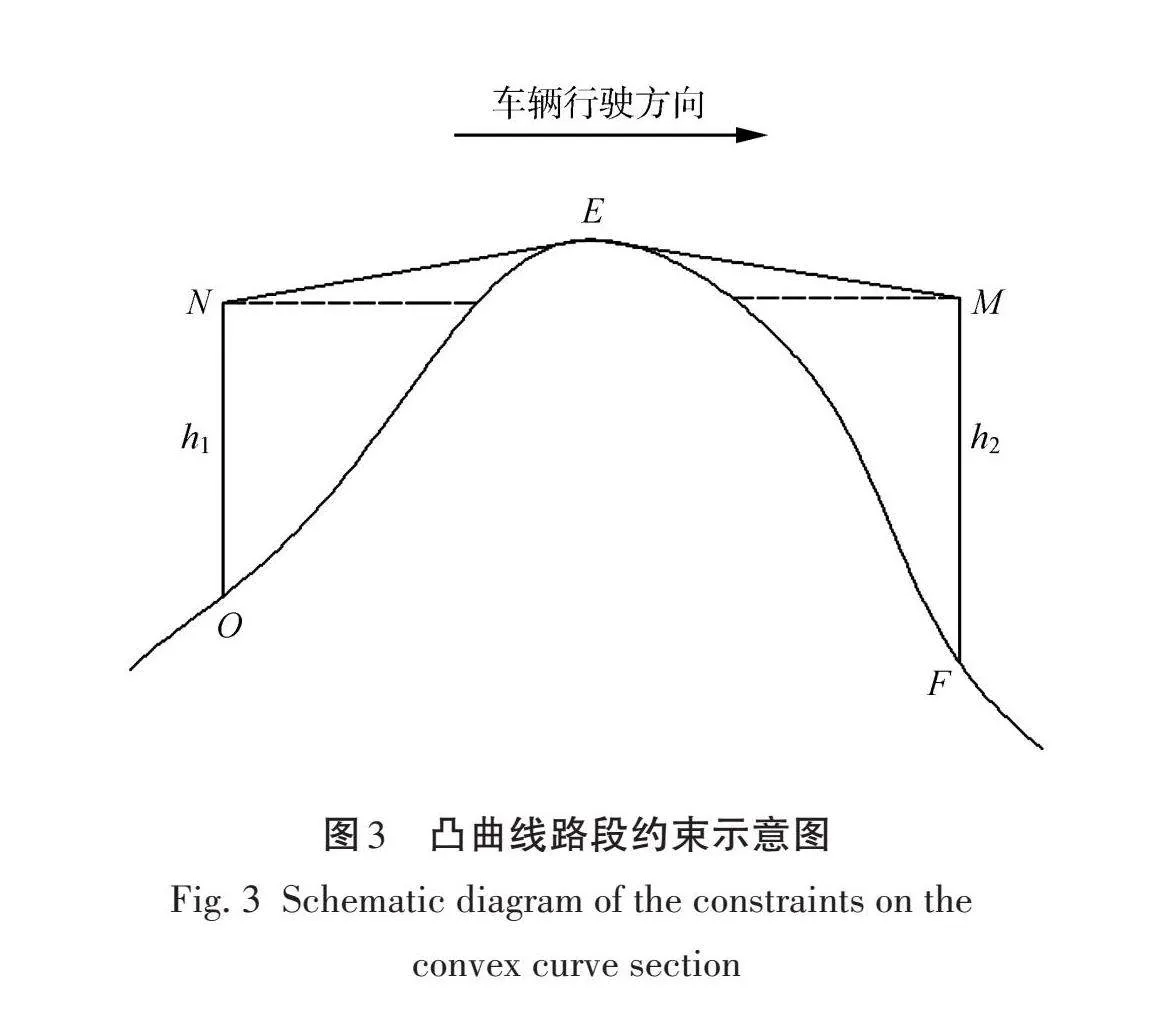
当车辆行驶在凸曲线路段时，驾驶员视距主要受到凸曲线坡顶点和驾驶员在坡顶的竖直动态视角限制，如图3所示，此时临界判定条件为

|φ_NE-φ_E |<δ且φ_NE≤θ。 （11）

φ_E=arctan（dZ_E）/√（〖d_xE〗^2+〖d_yE〗^2 ）。 （12）

φ_NE=arctan（Z_E-Z_N）/√（（x_E-x_N ）^2+（y_E-y_N ）^2 ）。 （13）

φ_NM=arctan（Z_M-Z_N）/√（（x_M-x_N ）^2+（y_M-y_N ）^2 ）。 （14）

式中：φ_NE为（NE） ⃗和水平面夹角，（°）；φ_NM为（NM） ⃗和水平面夹角，（°）；φ_E为坡顶点切线和水平面夹角，（°）；h1为驾驶员观测点高度，m；N为经视高修正后的点；M为经物高修正后的点。

2.3.2 凹曲线路段

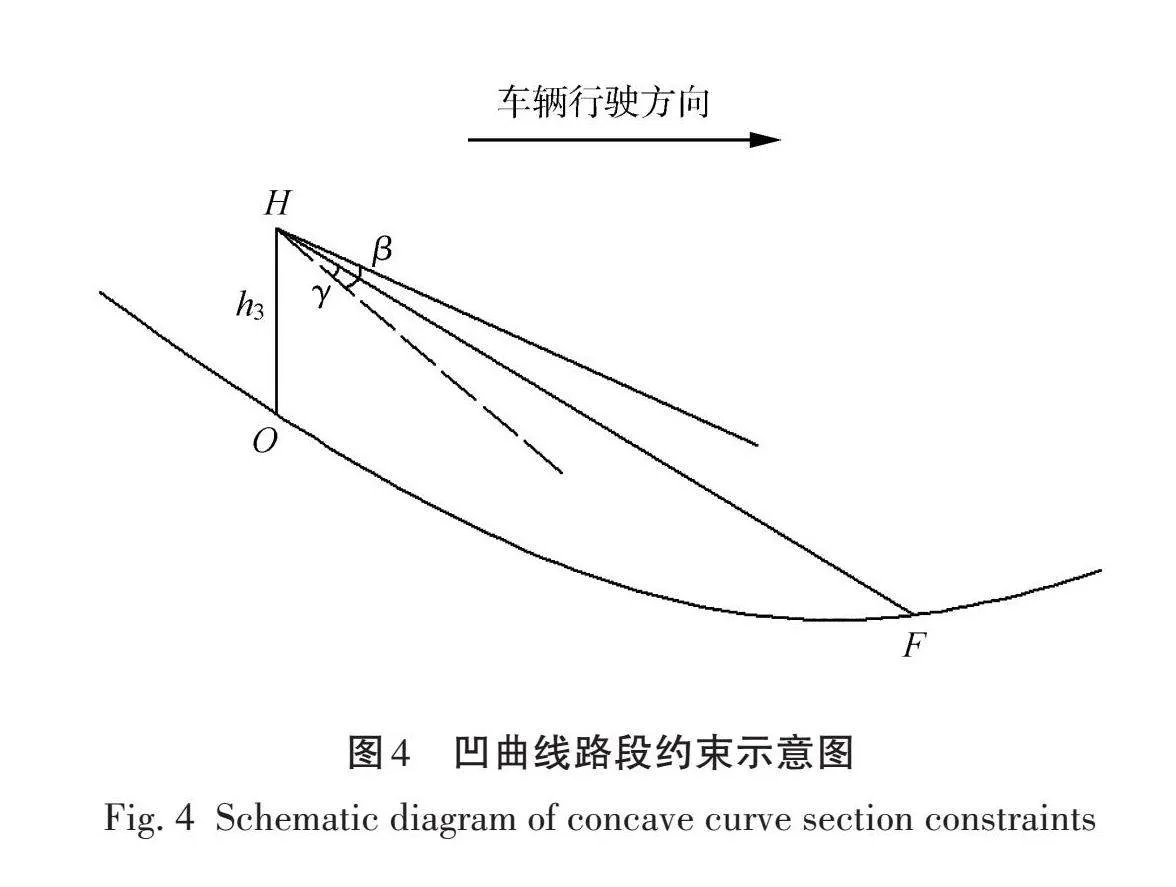
当车辆行驶在凹曲线路段时，驾驶员视距主要受到竖向最大视野角θ和车灯照射范围限制，如图4所示，此时临界判定条件为

|（|φ_HF-φ_O |-min（θ，γ） ）|<δ。 （15）

式中：φ_HF为（HF） ⃗和水平面夹角，（°）；φ_O为观测点O的切线和水平面夹角，（°）；γ为车前灯照射向上最 大照射角度，（°）；θ为驾驶员竖向向上最大视野 角，（°）；h3为车前灯高度，m；H为车前灯修正高度点。

2.4 林区曲线道路三维空间视距横向约束条件

当驾驶员观测点O和视距验算点F处于同一个水平面上时，如图5所示。采用横向约束条件约束，因周边林区树木遮挡，驾驶员视距主要受到圆曲线半径、车灯照射范围和横向最大视野影响［15］，临界判定条件为

|λ_OF-min（α，ε） |<δ。 （16）

2.5 林区曲线道路三维空间视距的确立

分析得出林区曲线道路三维空间视距模型为

S=min{S_max，∑_（k=j）^（j+1）▒[（x_（k+1）-x_k ）^2+（y_（k+1）-y_k ）^2+（z_（k+1）-z_k ）^2 ]^（1/2） }， {■（ϕ_（i，j）≤ϕ_max@ϕ_（i，j+1）>ϕ_max@j>n）┤。 （17）

式中：Smax为驾驶员视野可视最远距离，m；i为视距计算点标号；j为视距检查点标号；n为满足ϕi，k>ϕmax，∀k∈［1，n-1］且ϕ_（i，j）≤ϕ_max，k=n时为验算的第一个点；ϕ_max为驾驶员横向最大视野角，（°）。

2.6 林区曲线道路三维空间视距模型检验

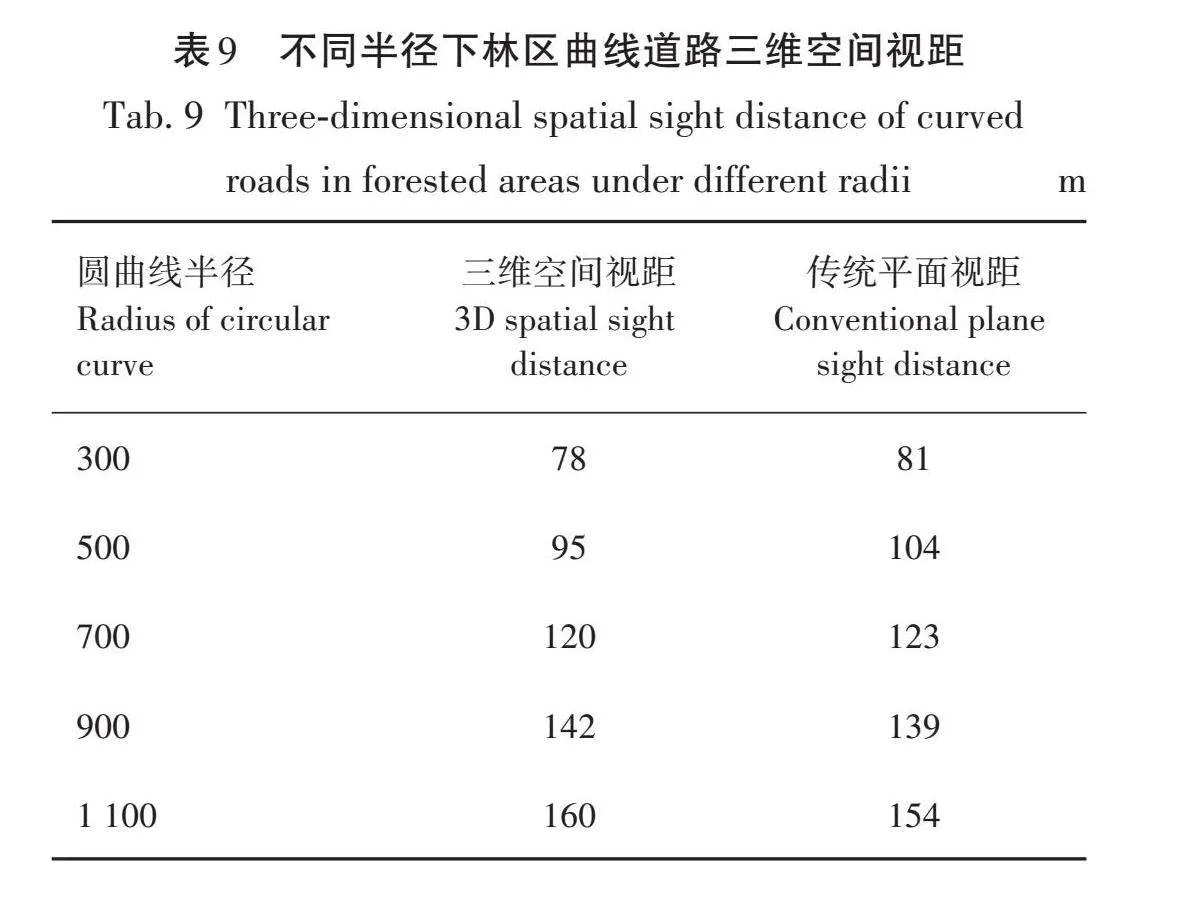
运用Matlab开发林区曲线道路计算程序，计算结果见表9。

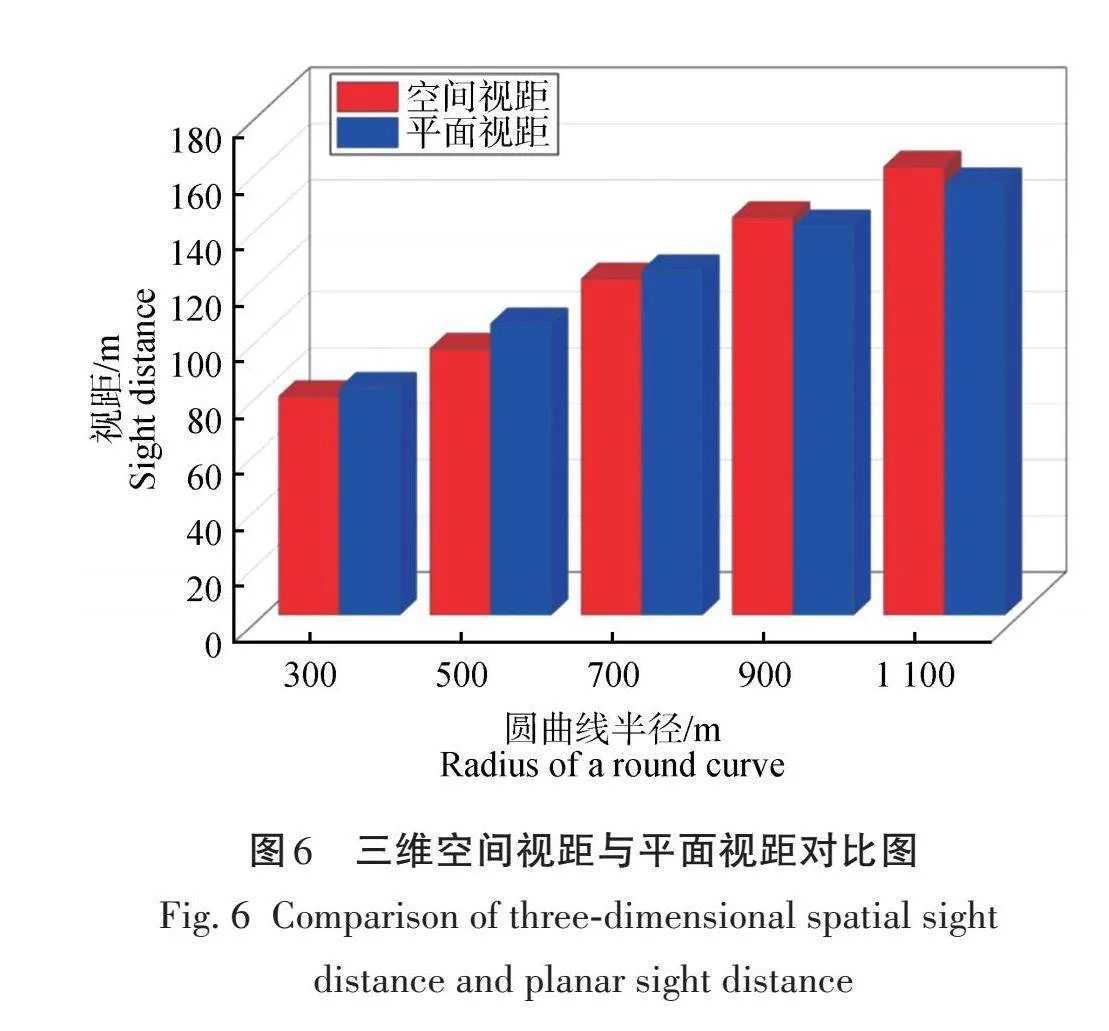
由图6可知，三维空间视距和传统平面视距的计算差值在±10以内，说明林区曲线道路三维空间视距模型较为合理。同时，圆曲线半径在700 m左右，三维空间视距在120 m左右时，三维空间视距是小于平面视距的，这时因为圆曲线半径较小，驾驶人员在驾驶车辆时受周边树木和自然环境影响较大，随着圆曲线半径的增大，三维空间视距和平面视距逐渐趋于一致。

3 试验方案

3.1 试验被试对象

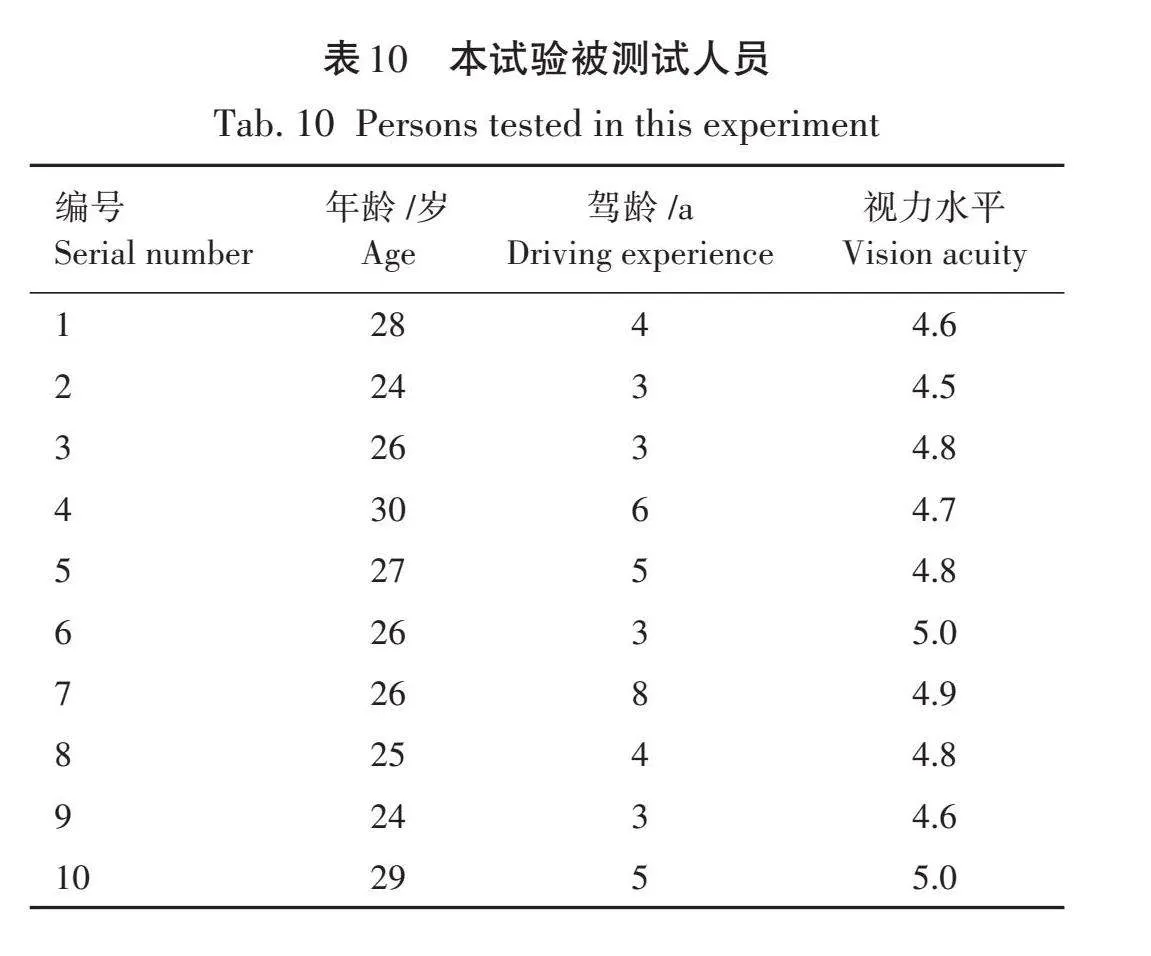
现有研究发现，由于个体的性格、年龄和反应能力等差异，导致不同程度的驾驶习惯，而对肇事者人员进行的相关研究也显示，导致车祸的主要年龄在18～25岁［16］。因此，基于预期方差、目标置信度和误差幅度来计算所需样本容量，计算公式如式（18）所示，招募10名有3 a以上驾驶经验的在读硕士和博士作为模拟驾驶人员，被测试人员信息见表10。

n≥（Zσ/e）^2。 （18）

式中：n为样本容量大小；Z为标准的正态分布统计；σ为标准偏差；e为最大误差。

3.2 试验设备

试验设备：模拟驾驶设备为德国WIVW研发的驾驶模拟器，眼动仪测试设备为SMART EYE公司研发的非接触式眼动追踪设备，生理记录仪为BIOPAC记录仪。

3.3 试验场景搭建

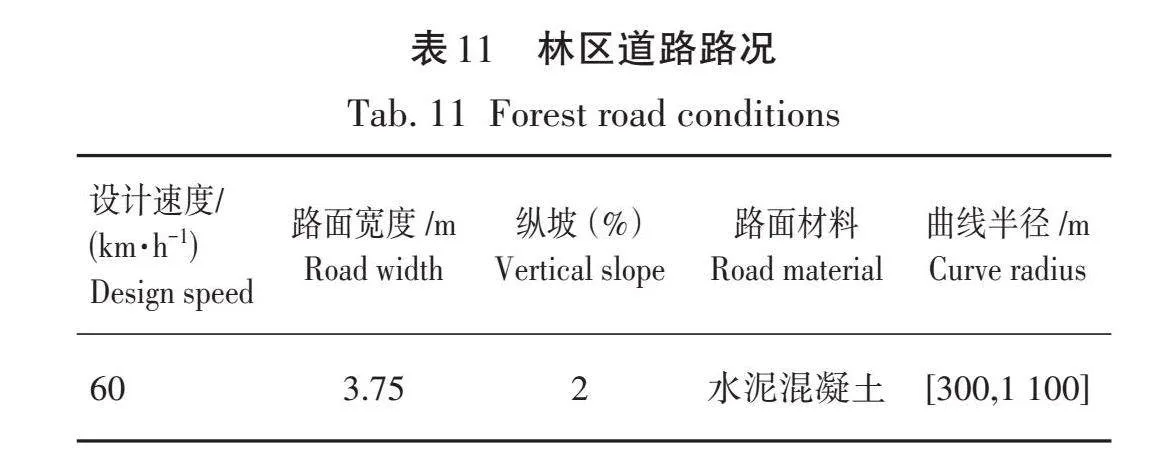
本次试验研究对象为通过SILABA Edit软件搭建曲线半径为300、500、700、900、1 100 m的林区曲线道路仿真路况，道路路况见表11。

3.4 试验流程

1）以实际道路为参照，构建不同曲线半径的驾驶模拟场景，确保试验结果真实合理。

2）选择符合试验要求的驾驶员，要求其在试验前的24 h禁止饮酒，保证数据的准确性，并对其进行20 min的模拟驾驶器实操培训，保证被测试人员能够适应模拟驾驶。

3）开启驾驶模拟器、眼动仪和生理记录仪，调整眼动仪对准驾驶员眼部和佩戴生理记录仪设备，并打开驾驶模拟场景。

4）驾驶员开始在模拟场景进行试验时，保证试验室内安静，无人与驾驶员进行交谈，防止对驾驶员产生干扰。

5）记录好驾驶员在驾驶时的眼动数据和心率数据，保证数据有效性，当数据无效时，会对驾驶员再次驾驶一次。

6）试验完成后，关闭设备，打扫试验室，保证下次试验便利。

4 试验数据分析

4.1 瞳孔直径分析

在行车过程中，驾驶员80%～90%的信息是通过瞳孔来获取的，其中95%的信息是不断变化的，驾驶员的动态视觉特征和交通事故有着紧密联系［17］。相关研究表明，一般情况下，瞳孔面积变化的主要影响因素为光照度的急剧变化和驾驶员心理因素。瞳孔面积是衡量人体负荷的灵敏指标，瞳孔直径变化能够准确描述驾驶员驾驶心生理负荷程度。

基于瞳孔直径指标，瞳孔面积变化率（U）也能够反应驾驶人员的行车状态，将驾驶行车状态分为舒适、较紧张和很紧张状态：舒适时U<20%；较紧张时20%≤U≤40%；很紧张时U>40%［18］。因为瞳孔形状近似于圆形，因此可以使用瞳孔直径大小变化百分比DTK进行驾驶安全性分析，瞳孔直径变化率计算公式为

D_TK=|D_i-D_0 |/D_0 ×100%。 （19）

式中：DTK为瞳孔直径变化率，%；Di为驾驶人在林区曲线道路行驶第i时刻的瞳孔直径，mm；D0为驾驶人不在驾驶状态下的瞳孔直径，mm。

对不同空间视距下的驾驶员通过曲线道路的瞳孔直径均值进行正态性检验和方差齐次检验，分析结果见表12、表13和图7，不同空间视距下驾驶员通过曲线道路瞳孔直径均值对应的P大于显著水平（P>0.05），数据均具有正态性，P-P图是根据变量的累积比例与指定分布的累积比例之间的关系所绘制的图形，由统计软件SPSS分析数据得出。

由表13可知，不同空间视距对应下驾驶员的瞳孔直径均值对应的P大于显著水平（P>0.05），表明不同空间视距下驾驶员瞳孔直径均值的变化性是一致的，因此具有方差齐性，满足单因素方差分析的前提条件，对不同空间视距下的驾驶员瞳孔直径均值进行单因素方差分析，分析结果见表14。

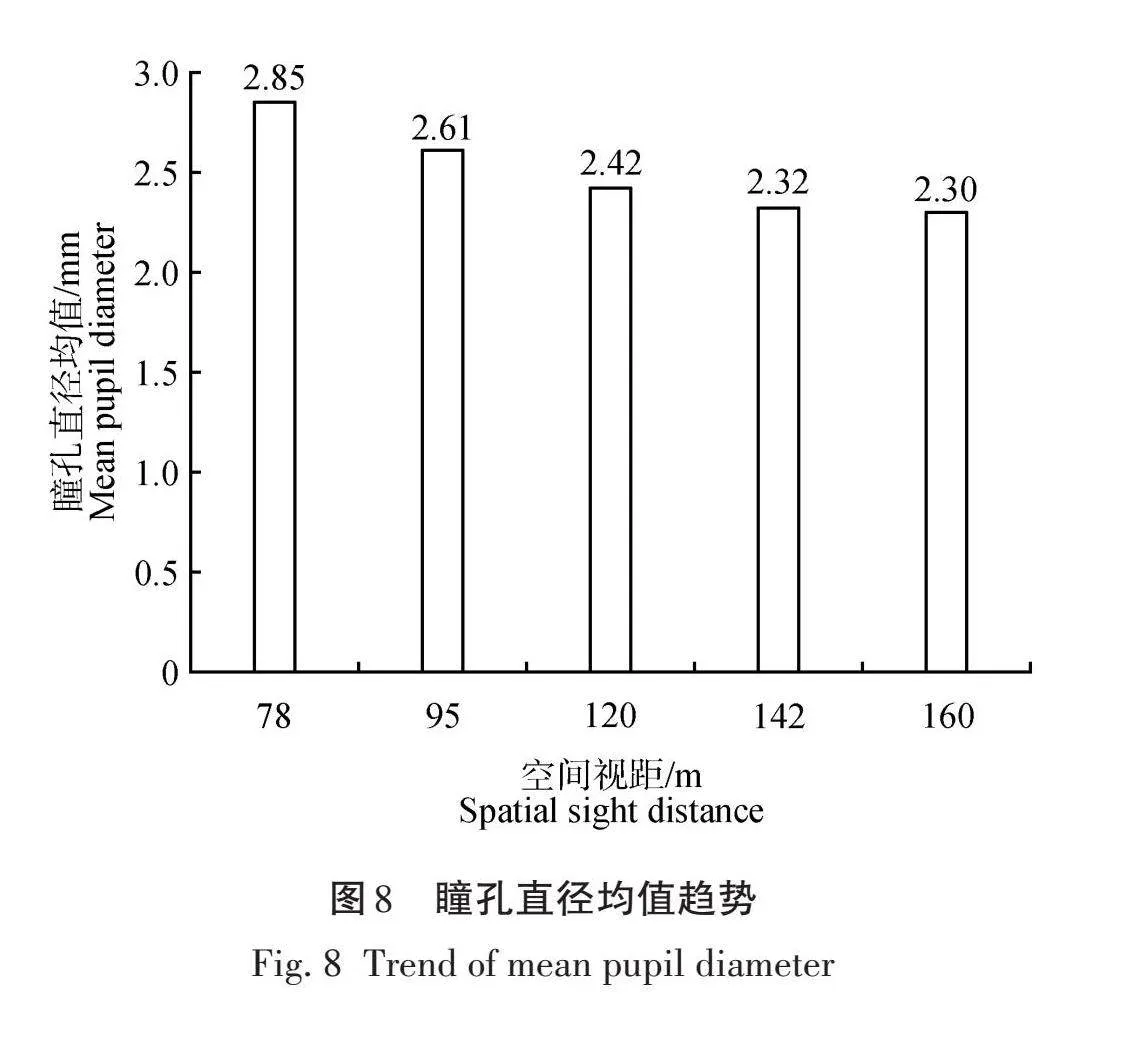
由表14可知，不同空间视距对应下驾驶员平瞳孔直径均值对应的P<0.05，表明不同空间视距对驾驶人瞳孔直径均值有着显著影响，不同空间视距下的驾驶人瞳孔直径均值变化如图8所示。

由图8可知，驾驶员瞳孔直径均值随着空间视距的增大而不断减小，呈负相关关系。这表明随着空间视距增大，驾驶员的驾驶压力不断减轻，紧张感减弱。在空间视距78～120 m，随着空间视距变化，驾驶员瞳孔直径均值变化较大，在空间达到120 m后，变化明显变小，表明120 m以上的空间视距满足驾驶员的行车视距需求，能够保证比较轻松的驾驶状态。

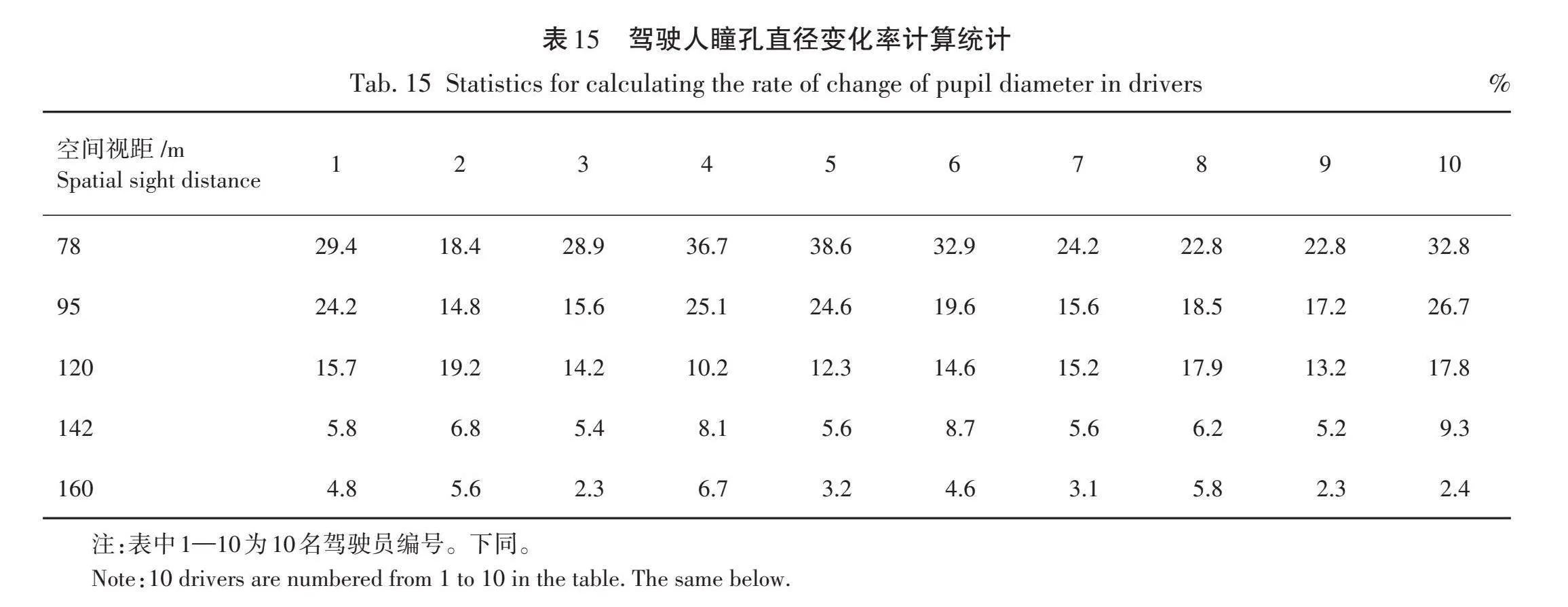
根据式（19）对所测得的不同空间视距下的瞳孔直径值进行计算，求出瞳孔直径变化率值，计算结果见表15。

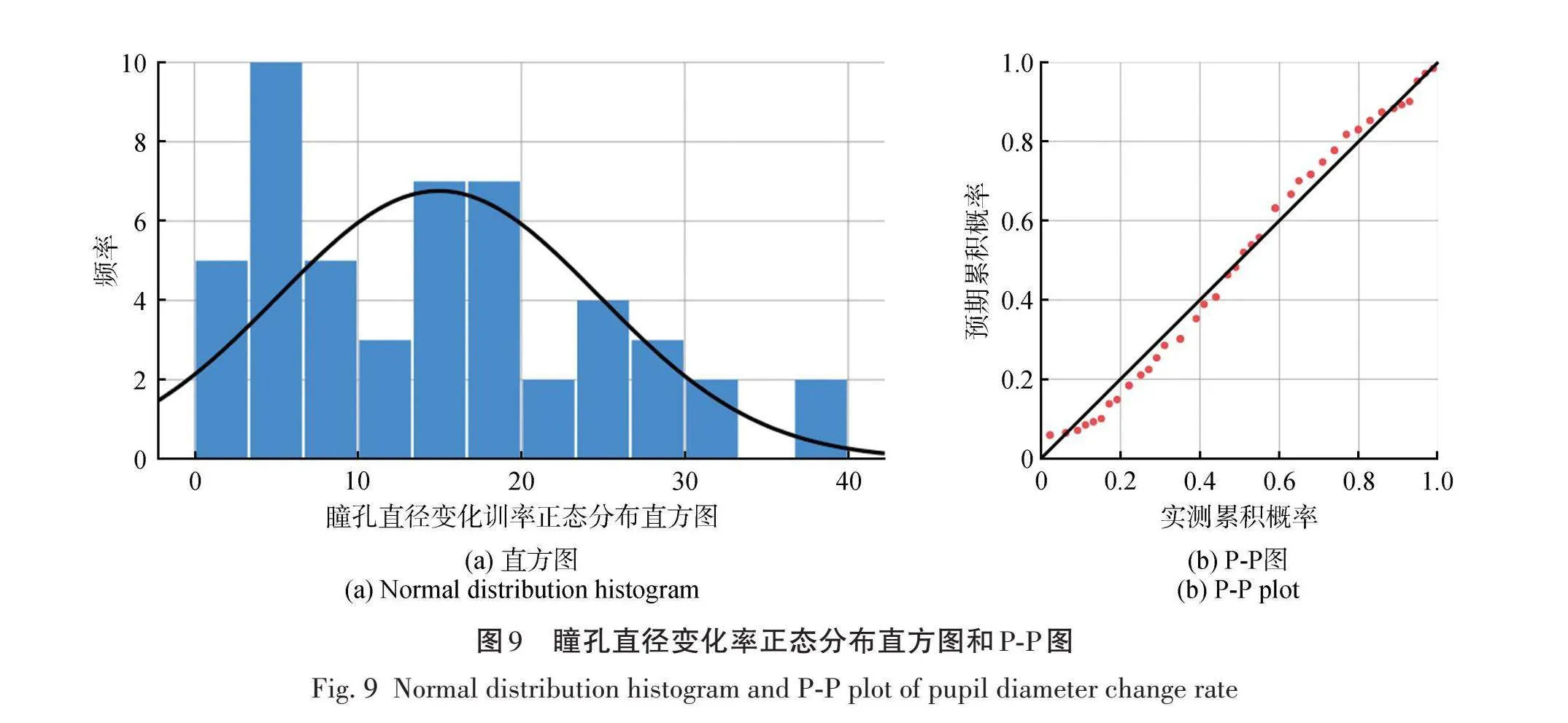
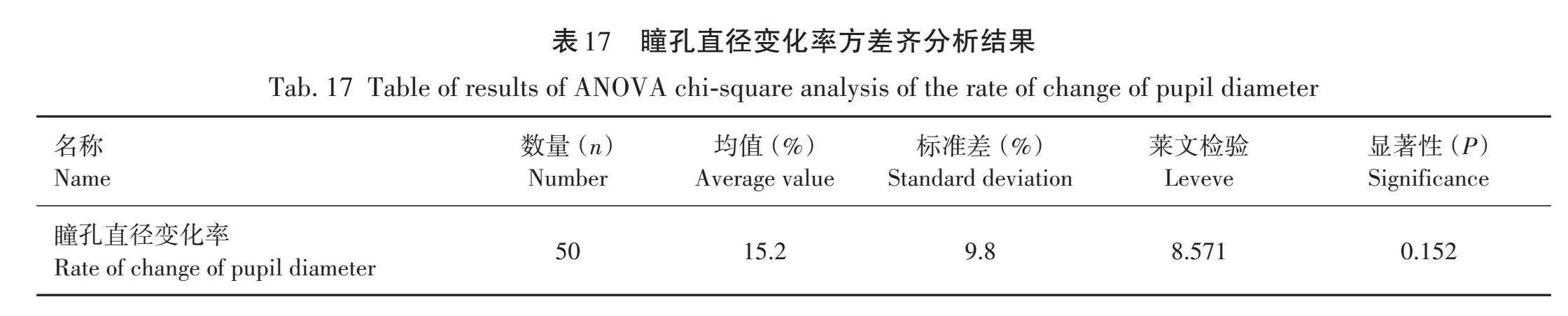
对表15的瞳孔直径变化率进行正态性检验和方差齐次检验，检验结果见表16、表17和图9，在不同空间视距下驾驶员瞳孔直径变化率对应的P值小于显著水平（P<0.05），数据不具有严格的正态性。但是数据峰度小于3，并且偏度接近于0，考虑到仿真试验的误差性和真实性，所以可以近似看作是正态分布。

由表17可知，不同空间视距对应下驾驶员的瞳孔直径变化率对应的P大于显著水平（P>0.05），表明不同空间视距下驾驶员瞳孔直径变化率变化性是一致的，因此具有方差齐性，满足单因素方差分析的前提条件，对不同空间视距下的驾驶员瞳孔直径均值进行单因素方差分析，分析结果见表18。

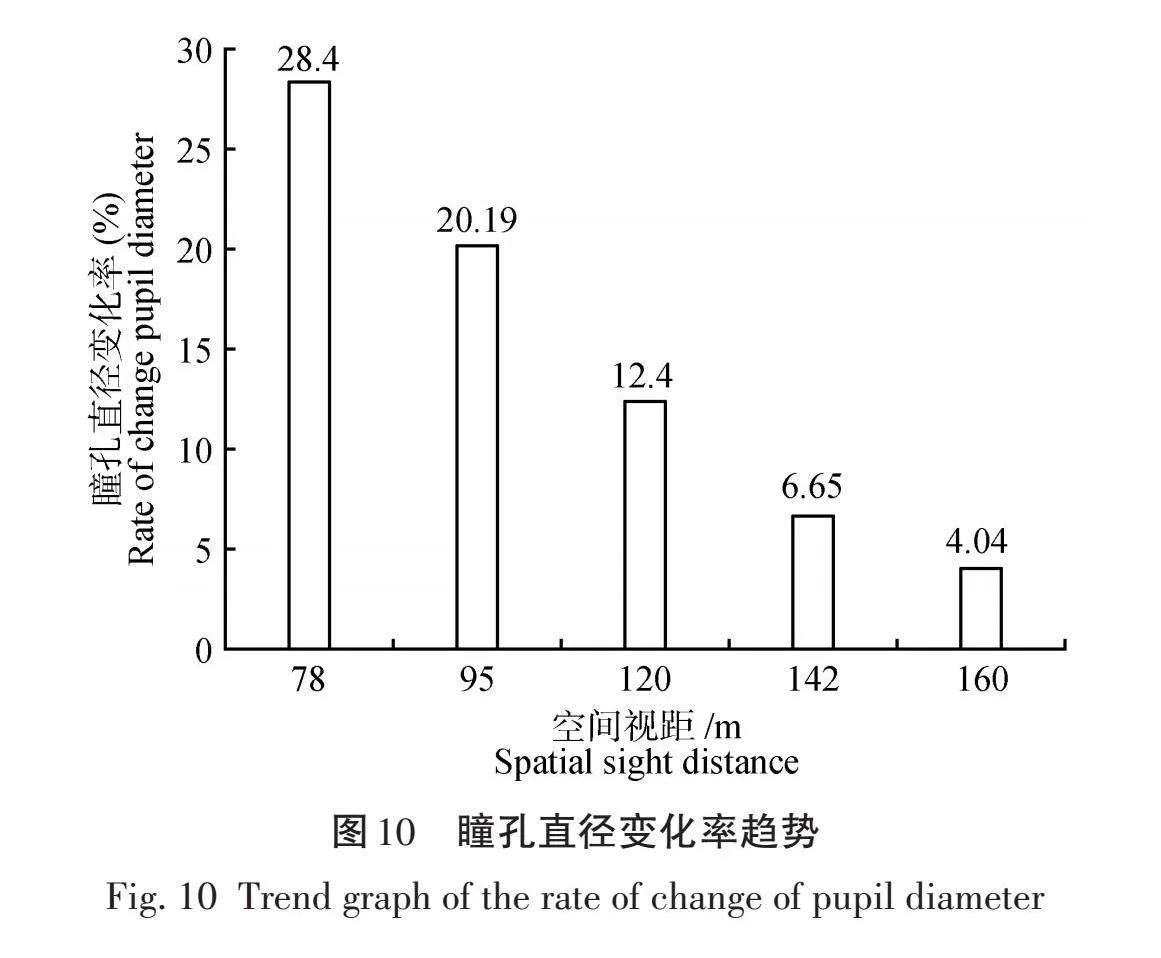
由表18可知，不同空间视距对应下驾驶员瞳孔直径变化率对应的P<0.05，表明不同空间视距对驾驶人瞳孔直径变化率有着显著影响，不同空间视距下的驾驶人瞳孔直径变化率变化趋势如图10所示。

由图10可知，驾驶员瞳孔直径变化率随着空间视距的增大而不断减小，代表着瞳孔直径变化波动变小。在空间视距为78、95 m时，驾驶员瞳孔直径变化率较大，瞳孔直径波动较大，分别为28.4%、20.19%，在空间视距为142、160 m时，驾驶员瞳孔直径变化率为6.65%、4.04%，瞳孔直径波动较小，这说明随着空间视距的增大，驾驶员的驾驶舒适性不断提高，驾驶负荷不断减小。

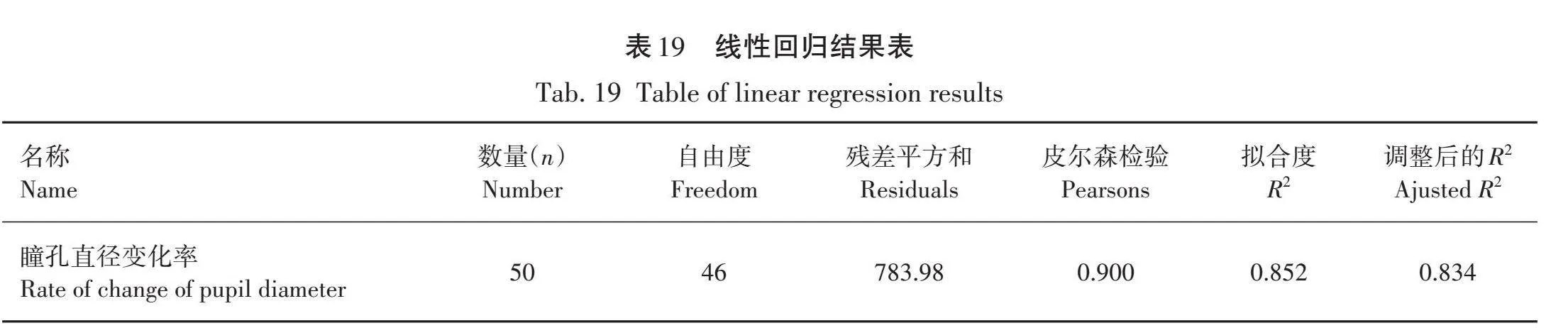
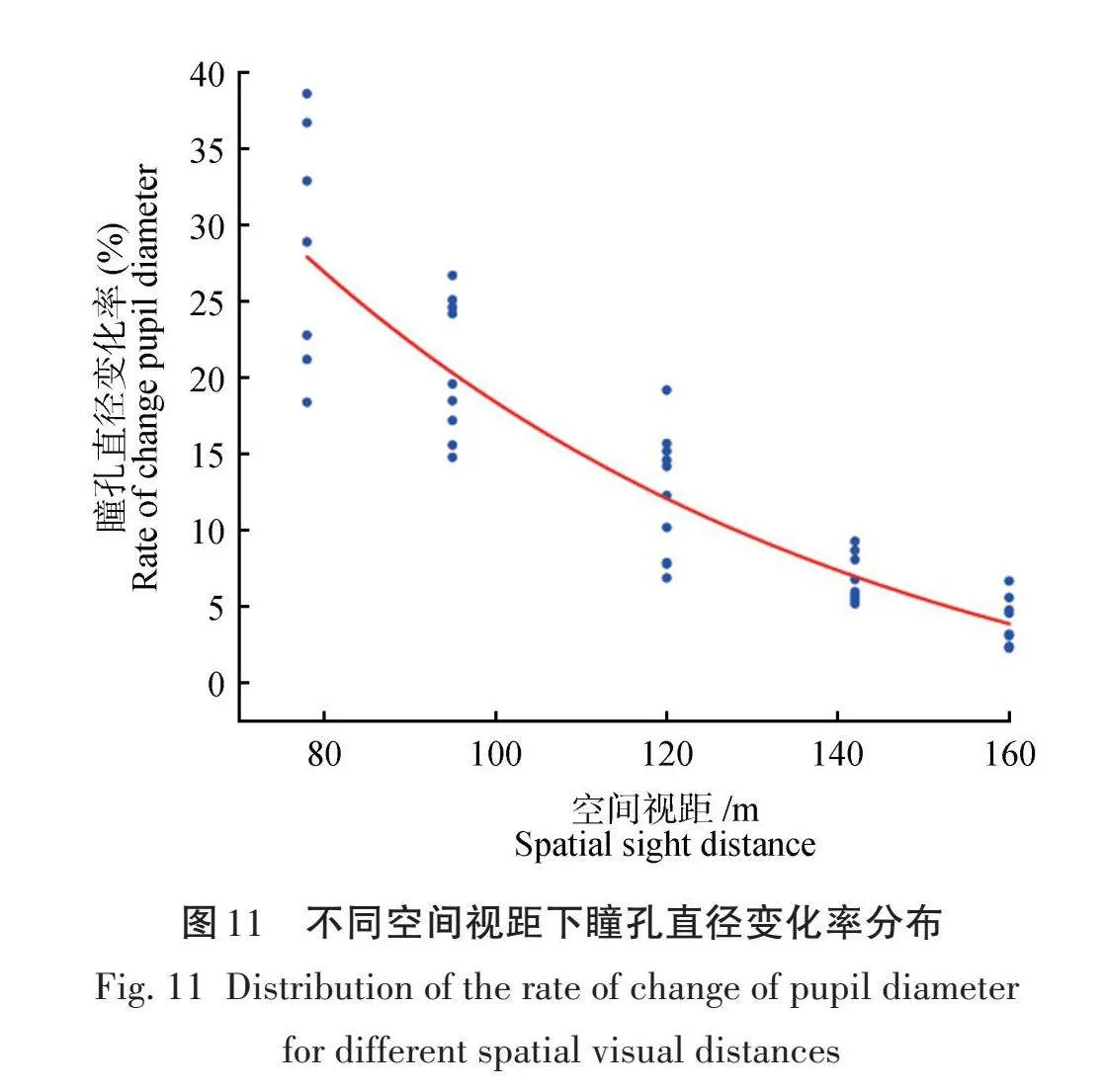
为了探究空间视距与瞳孔直径变化率的关系，利用spss绘制散点图，如图11所示，瞳孔直径变化率和空间视距呈现非线性关系，选择非线性函数进行拟合，拟合结果见表19。

由表19可知，调整后的R2为0.834，回归效果较好，不同空间视距和瞳孔直径变化率的关系式如式（20）所示。

D_TK=108.57×e^（（-S_SJ/67.48） ）-6.24。 （20）

式中：DTK为瞳孔直径变化率，%；SSJ为三维空间视距，m。

相关研究已经将驾驶员瞳孔直径变化率与驾驶员行车舒适性阈值之间关系进行了标定［19］，具体关系见表20。

瞳孔直径变化率大小代表着驾驶员的紧张程度，也代表着行车舒适性，根据表20以10%～18%作为行车舒适阈值区间，基于瞳孔直径变化率的空间视距推荐值见表21。

4.2 林区曲线道路驾驶员心率特性行为分析

心率（Heart rate，HR）是一个正常人心脏每分钟跳动的频率，通常在60～100次，正常的人在安静的时候会心跳比较缓慢，但是在高负荷工作、紧张或者疲劳的时候，心跳会加速，心率会超过100次/min［20］。当人处于紧张或疲劳状态时，心率会迅速增加到100次/min以上。相关研究表明驾驶人驾驶负荷越大时，情绪越紧张，心率增长率越大，可以使用心率增长率来代表驾驶员的驾驶负荷情况。心率增长率计算如式（21）所示。

H_RI=（H_R2-H_R1）/H_R1 ×100%。 （21）

式中：HRI为驾驶员心率增长率，%；HR1为驾驶员静息心率，次/min；HR2为驾驶员通过林区曲线道路的平均心率，次/min。

将对生理记录仪所测心电数据导入Acqkonwlege5.0软件，根据时间对应的HR数据代入式（21），得到不同空间视距下驾驶员心率增长率见表22。

对表22的心率增长率进行正态性检验和方差齐次检验，检验结果见表23和表24，在不同空间视距下驾驶员心率增长率对应的P大于显著水平（P>0.05），数据均具有正态性。

由表24所知，不同空间视距对应下驾驶员心率增长率对应的P大于显著水平（P>0.05），表明不同空间视距下驾驶员心率增长率的变化性是一致的，因此具有方差齐性，满足单因素方差分析的前提条件，对不同空间视距下的驾驶员心率增长率进行单因素方差分析，分析结果见表25。

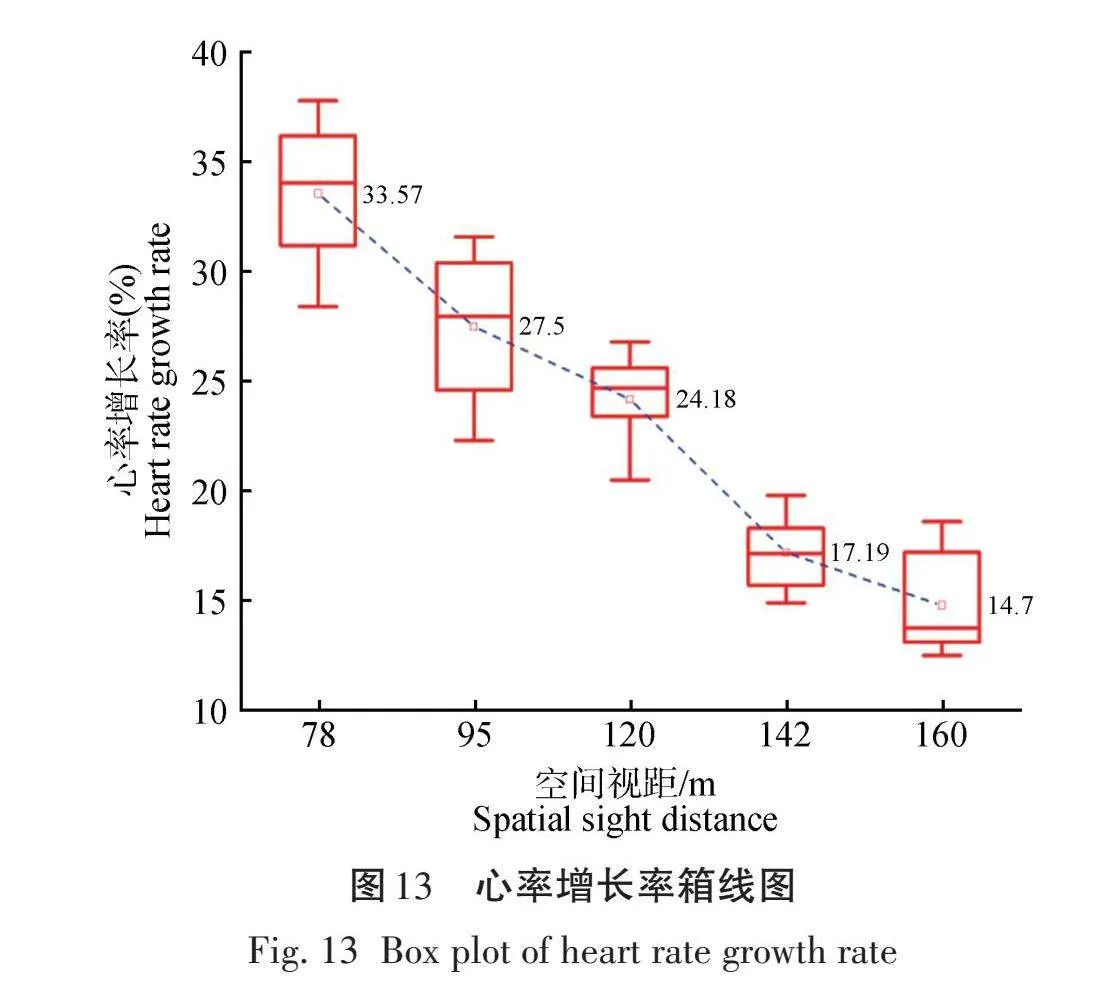
由23表可知，不同空间视距对应下驾驶员心率增长率对应的P<0.05，表明不同空间视距对驾驶人心率增长率有着显著影响。不同空间视距下的驾驶人心率增长率变化趋势如图13所示。

由图13可知，驾驶员心率增长率随着空间视距的增大而不断减小，代表着在空间视距为78、95 m时，驾驶员心率增长率较大，心率波动较大，分别为33.57%、27.5%，在空间视距为142 、160 m时，驾驶员心率增长率为17.19%、14.78%，心率波动较小，这说明随着空间视距的增大，驾驶员的驾驶舒适性不断提高，驾驶负荷不断减小。

为探究空间视距与心率增长率的关系，利用spss绘制散点图，如图14所示，心率增长率和空间视距呈现非线性关系，选择非线性函数进行拟合，拟合结果见表26。

由表26可知，调整后的R2为0.828，回归效果较好，因此可得到不同空间视距和心率增长率的关系式如式（22）所示。

H_RI=76.698×e^（（-S_SJ/177.66） ）-16.49。 （22）

式中：HRI为驾驶员心率增长率，%；SSJ为三维空间视距，m。

乔建刚［21］通过驾驶模拟仓和心电仪的有机结合，提出驾驶员紧张度的理论区域和心率增长率的紧张度阈值。HRI<20%时，驾驶员感受为舒适； 20%≤HRI≤30%，驾驶员感受为较紧张；30%<HRI，驾驶员感受为特别紧张。

考虑到在林区曲线道路行驶中，需要驾驶员保持一定的紧张程度来保证行车安全性，所以选择20%～30%心率增长率为林区曲线道路空间视距适宜值推荐范围，最小空间视距为89 m，适宜空间视距为132 m。

5 结论

通过驾驶模拟试验，对比分析不同空间视距下的林区曲线道路驾驶员行车舒适性研究，得出以下结论。

1）建立林区曲线道路空间视距模型，并和现有的二维空间视距进行对比，误差较小，适用于设计速度为60 km/h的林区曲线道路

2）根据瞳孔直径均值和瞳孔直径变化率，驾驶员瞳孔直径变化率随着空间视距的增大而不断减小，瞳孔直径波动变小，驾驶员驾驶负荷减小，驾驶舒适性不断提高，依据瞳孔直径变化率行车舒适阈值，得出考虑瞳孔直径变化率的最小空间视距为101 m，适宜空间视距为128 m。

3）根据心率增长率，驾驶员心率增长率随着空间视距增大而不断减小，驾驶员驾驶舒适性不断提高，依据心率增长率紧张度阈值，得出考虑心率增长率的最小空间视距为89 m，适宜空间视距为132 m。

【参 考 文 献】

［1］ 王万丰.我国道路交通安全事故统计分析［J］.中国安全生产，2020，15（3）：52-53.

WANG W F.Statistical analysis of road traffic safety accidents in China［J］.China Safety Production，2020，15（3）：52-53.

［2］ 郭根胜，朱守林，戚春华，等.北方林区冰雪路面平面线形驾驶员心电特性研究［J］.中国科技论文，2013，8（11）：1110-1114.

GUO G S，ZHU S L，QI C H，et al.Driver′s ECG characteristics on horizontal alignment of snow-covered road in forest region of northern China［J］.Chinese Science and Technology Paper，2013，8（11）：1110-1114.

［3］ 胡顺峰.山区高速公路隧道群交通事故特征及致因机理分析［J］.公路，2016，61（5）：134-138.

HU S F.Traffic accident characteristics and mechanism analysis of mountain highway tunnel group［J］.Highway，2016，61（5）：134-138.

［4］ CHUNG B J，PARK J B，KIM J Y，et al.Limit length evaluation of tangent on freeway according to driver's physiological response［C］//TRB Annual Meeting，2001：1-8.

［5］ FOY H J，CHAPMAN P.Mental workload is reflected in driver behaviour，physiology，eye movements and prefrontal cortex activation［J］.Applied Ergonomics，2018，73：90-99.

［6］ 郭根胜.基于驾驶员心理生理反应的北方林区公路平曲线半径研究［D］.呼和浩特：内蒙古农业大学，2008.

GUO G S.A study on the radius of flat curve of northern forest highway based on drivers′ psychophysiological responses［D］.Huhhot：Inner Mongolia Agricultural University，2008.

［7］ 王进州，艾力·斯木吐拉.基于驾驶员生理负荷的高原公路转角值安全风险评价［J］.科学技术与工程，2020，20（7）：2939-2943.

WANG J Z，AILI SMUTULA.Safety risk assessment of plateau highway corner value based on driver′s physiological load［J］.Science，Technology and Engineering，2020，20（7）：2939-2943.

［8］ 乔建刚，董进国，陶瑞，等.基于心生理反应的山区高速公路线形安全分析［J］.科学技术与工程，2023，23（7）：3066-3074.

QIAO J G，DONG J G，TAO R，et al.Alignment safety analysis of mountainous expressway based on physiological reaction［J］.Science，Technology and Engineering，2023，23（7）：3066-3074.

［9］ 潘晓东，杜志刚，蒋宏，等.驾驶员心率和血压变动与山区公路线形关系的实验研究［J］.人类工效学，2006，12（2）：16-18，30.

PAN X D，DU Z G，JIANG H，et al.Experiment research on relationship between the variation of drivers′ heart rate and systolic blood pressure and alignment of mountainous highway［J］.Chinese Journal of Ergonomics，2006，12（2）：16-18，30.

［10］ WILSON G F.An analysis of mental workload in pilots during flight using multiple psychophysiological measures［J］.International Journal of Aviation Psychology，2002，12（1）：3-18.

［11］ 朱蓉.基于驾驶员动视角特性的道路空间动态视距模型研究［D］.长沙：长沙理工大学，2016.

ZHU R.Research on dynamic sight distance modeling in road space based on driver′s dynamic viewpoint characteristics［D］.Changsha：Changsha University of Science and Technology，2016.

［12］ 孙璐，秦玉秀，游克思，等.基于可靠度的隧道行车视距影响因素分析［J］.东南大学学报（自然科学版），2014，44（4）：859-863.

SUN L，QIN Y X，YOU K S，et al.Reliability-based risk analysis of sight distance influence factors in tunnel［J］.Journal of Southeast University（Natural Science Edition），2014，44（4）：859-863.

［13］ 赵永平，杨少伟，吴华金，等.山区高速公路螺旋展线隧道内平曲线最小半径［J］.长安大学学报（自然科学版），2007，（6）：72-75.

ZHAO Y P，YANG S W，WU H J，et al.Helix line development's minimum radius of horizontalcurve in freeway tunnel［J］.Journal of Chang′an University（Natural Science Edition），2007（6）：72-75.

［14］ 廖军洪，邵春福，邬洪波，等.公路三维动态视距计算方法及评价技术［J］.吉林大学学报（工学版），2013，43（3）：640-645.

LIAO J H，SHAO C F，WU H B，et al.Calculation and assessment technique of highway 3D dynamic sight distance［J］.Journal of Jilin University（Engineering and Technology Edition），2013，43（3）：640-645.

［15］ 严考权，王烨，胡炜.曲线隧道三维动态视距研究［J］.交通科技，2019（2）：115-119.

YAN K Q，WANG Y，HU W.Research on three-dimensional dynamic sight distance in curved tunnels［J］.Transportation Science and Technology，2019（2）：115-119.

［16］ 杨颜菲.驾驶员个人因素和驾驶经验对驾驶愤怒的影响［D］.武汉：武汉科技大学，2018.

YANG Y F.Effects of drivers′ personal factors and driving experience on driving anger［D］.Wuhan：Wuhan University of Science and Technology，2018.

［17］ 赵亮，胡江碧.眼动与驾驶行为的相关性分析.proceedings of the 2008第四届中国智能交通年会［C］.青岛：山东交通学院，2008.

ZHAO L，HU J B.Correlation analysis of eye movements and driving behavior［C］//Proceedings of the 2008 4th Annual China Intelligent Transportation Conference.Qingdao：Shandong Jiaotong University，2008.

［18］ 陶盼盼，于海臣，赵晓华，等.高速公路隧道入口段减速标线与红色警示路面减速效果及舒适性研究［J］.公路，2019，64（1）：157-163.

TAO P P，YU H C，ZHAO X H，et al.Research of the deceleration effect and comfort of deceleration marking and red alert pavement on expressway tunnel entrance section［J］.Highway，2019，64（1）：157-163.

［19］ 叶飞，张兴冰，苏恩杰，等.基于驾驶舒适性的公路隧道侧壁装饰研究［J］.现代隧道技术，2022，59（4）：196-203.

YE F，ZHANG X B，SU E J，et al.Sidewall decoration for highway tunnels based on driving comfort［J］.Modern Tunnelling Technology，2022，59（4）：196-20

［20］ 朱可宁.基于HRV的高速公路隧道环境对驾驶行为影响研究［D］.西安：长安大学，2019.

ZHU K N.Research on the influence of highway tunnel environment on driving behavior based on HRV［D］.Xi′an：Chang′an University，2019.

［21］ 乔建刚.基于驾驶员因素的山区双车道公路关键参数研究［D］.北京：北京工业大学，2006.

QIAO J G.Research on key parameters of mountainous two-lane highway based on driver factors［D］.Beijing：Beijing Institute of Technology，2006.