基于木材振动特性的月琴声学品质广义回归神经网络预测模型

摘 要：泡桐木始终是制造乐器谐振元件的重要材料，对乐器的音质有着重要的影响。采用广义回归神经网络（General Regression Neural Network，GRNN）建立基于共鸣板振动性能的月琴音质评价模型。以制造出的9把月琴为研究对象，根据月琴的音质评价以及制备月琴的共鸣板信息，提出月琴音质的预测模型。在180组数据中，随机抽取135组数据进行训练，其余45组数据进行验证。使用主成分分析方法、GRNN建立月琴声学质量评价模型，并进行仿真预测。结果表明，基于共鸣板的振动特性，利用Matlab仿真可以实现对月琴音质的预测，预测的准确率可达到91.41%。此外，研究还表明，泡桐木共鸣板的动态弹性模量、声辐射阻尼系数、弹性模量、剪切模量比、声阻抗，损耗角正切和声转化率等参数均是影响其制备成品月琴声学质量的重要因素。

关键词：广义回归神经网络； 主成分分析； 声学品质； 振动特性； 共鸣板； 木材； 民族乐器

中图分类号：S781.28 文献标识码：A DOI：10.7525/j.issn.1006-8023.2024.04.017

Research on GRNN Prediction Model for Acoustic Quality of Yueqin Based on Wood Vibration Characteristics

YANG Yang

（Harbin University， Harbin 150076， China）

Abstract： Paulownia has usually been an important material for making resonant components of musical instruments， which has a significant influence on the sound quality of musical instruments. This study utilized a generalized regression neural network （GRNN） to develop the sound quality evaluation model of Yueqin based on the vibration performance of the soundboard. In this study， nine Yueqins were fabricated， and a prediction model for the sound quality of Yueqins was proposed based on their sound quality evaluation and the soundboard information of prepared Yueqins. Out of a total of 180 sets of data， 135 sets of data were randomly selected for training and the remaining 45 sets of data were used for validation. A model for evaluating the acoustic quality of Yueqin instruments was established using principal component analysis method and GRNN， and simulation prediction was performed. The results showed that based on the vibration characteristics of the soundboard， the prediction of the Yueqin sound quality can be achieved by using the Matlab simulation， and the accuracy of the prediction can reach 91.41%. In addition， this study demonstrated that the dynamic elastic modulus， acoustic radiation damping coefficient， elastic modulus， elastic and shear modulus ratio， acoustic impedance， loss tangent angle， and acoustic conversion efficiency of Paulownia wood resonator plates were all key factors influencing the acoustic quality of the finished Yueqin during its preparation.

Keywords： Generalized regression neural network； principal component analysis； acoustical quality； vibration characteristics； soundboard； wood； national musical instrument

0 引言

由于木材具有良好的振动特性，千百年来，一直被用作重要的共鸣乐器材料。木材独特而恰当的物理特性使其成为至今为止乐器的主要用料［1］。由于木材的过度消耗，乐器的成本迅速增加，有必要寻找替代材料来制造传统乐器。作为木材的替代品，一些木质复合材料被开发用于小提琴顶板、吉他、打击乐器［2-4］。然而，新材料的性能是相对不确定的，其性能相对难以预测。因此，希望根据原材料的音板振动性能，开发一个预测乐器声学质量的模型。

木材表面冲击或激励引起的振动反应与木材的声学特性和结构有关。Norimoto等［5］、Matsunaga等［6］和Yoshitaka等［7-8］通过研究木材作为声板的振动特性，发现木材的声学特性受到振动特性参数的显著影响。从声学适应性、审美适宜性和综合评价的角度对小提琴进行了等级划分，采用了Buksnowitz等［9］的主观评价方法。用多元线性回归方法测定了材料的声速、声阻尼系数、共振频率、动弹模数、硬度、密度、年轮宽度、树轮宽度变系数、含水率、纤维长度和尺寸稳定性等材料性能指标，并对材料性能进行了分析。用Traore等［10］提出的自由弯曲振动（free-free flexural vibration）测定了单板木材的主要声学性质。

近年来，以统计学习理论为基础的乐器声学质量预测模型引起了相关专家越来越多的兴趣。Wong等［11］以马来西亚沙捞越地区的一种传统弦乐器为研究对象，利用机器学习理论，筛选出制作沙贝音板的最佳木材，通过振动试验，获得9种木材样品的声音数据及其特征，并使用支持向量机（SVM）算法通过所选的13个特征对木材类型和木材等级进行分类，最终确定了一种当地特有的具有较高响度的轻质硬木作为制作沙贝的最佳音板材料。Liu［12］运用人工神经网络的理论，对乐器的声学质量进行评价，提取常数Q（Constant Q Transform，CQT）和梅尔倒谱系数（MFCC）作为音符信号特征，将单特征和组合特征作为Softmax回归BP（Softmax Regression Back Propagation）神经网络多分类识别器的输入，把标准音的分类编码定义为监督网络学习的目标；该归一化指数函数的算法是将25个音符从低音到高音准确识别，平均识别率可达95.6%；与其他识别算法相比，该算法具有约束条件少、音符范围广和识别率高等优势。杨扬等［13］对琵琶共鸣板素材的振动特性进行检测，利用随机森林算法建立了共鸣板素材振动特性的琵琶声学品质预测模型，得到的准确率为87.99%。Huang等［14］采用高斯混合模型（GMM）和支持向量机（SVM）对民族乐器用木材的振动信号进行分类和识别，结果表明高斯混合模型和支持向量机结合的木材振动信号识别率高达90%以上。

广义回归神经网络（General Regression Neural Network，GRNN）是一种高效率的机器学习方法，因其具有对训练数据量要求少、训练速度快和预测精度高等众多优势而被广泛用于预测相关的研究中。Kaffash等［15］提出了一个自适应GRNN来估计道路事故的风险。该混合预测模型通过考虑22个不同的预测变量（特征）来估计道路事故风险，包括地理特征、时间条件、天气条件、道路相关特征、车辆相关特征以及基于权威数据源和志愿地理信息（VGI）计算的驾驶员特征，在不同道路环境的情景下对该方法的评估表明，该方法预测的事故风险具有非常高的准确性（平均准确率约为90.74%）。Sridharan等［16］运用GRNN模型对瞬态太阳能平板集热系统（SFPCS）的热能性进行了预测，通过训练、测试和验证，得到的准确率较高，可以达到98%。

GRNN有着较好的泛化性，在多变量预测中具有较好的效果。因此本研究开发了一种基于GRNN模型的月琴声学品质预测模型，对我国各种民族乐器声学品质预测模型进行完善和探究，从月琴共鸣板素材的振动特性参数研究出发，通过对木质共鸣板素材进行检测，准确预测由这些共鸣板素材制作的月琴的声学品质。此外，还采用主成分分析法（Principal Component Analysis，PCA）对用于共鸣板素材的振动特性参数进行降维处理，归纳出对该预测问题最相关的参数，为制作月琴材料的选择提供科学理论基础和选材的有效途径。

1 材料和方法

1.1 月琴的制备与数据采集

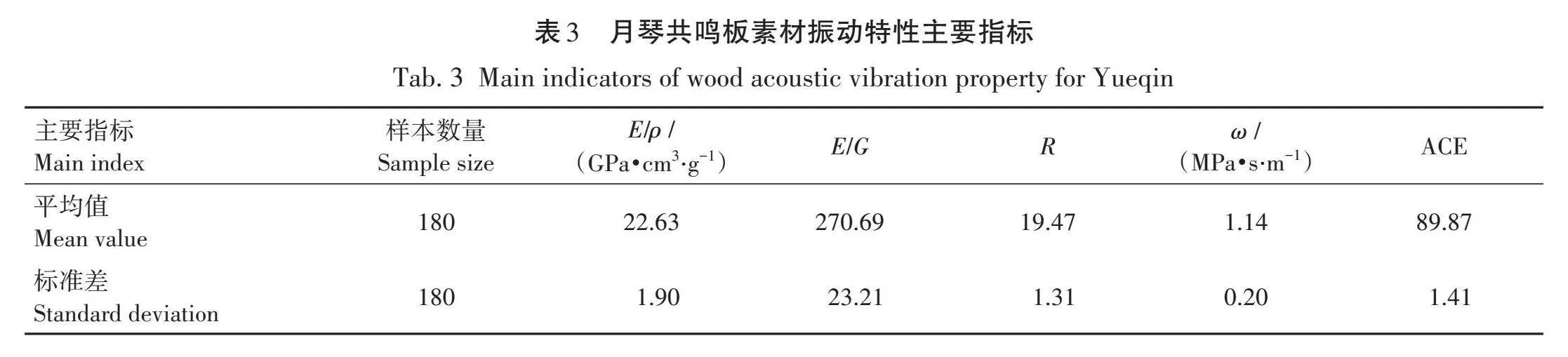
本研究中使用了泡桐木制成的共鸣板素材由天津市第一民族乐器厂提供，用于制作共鸣板素材的木料经过风干，使其含水率低于16%。木料的规格及尺寸见表1。其中试验中使用CF-5220Z为日本ONO SOKKI公司生产的双通道快速傅里叶变换分析仪。试验中还使用了声级计（TES-1350A）以及加速度传感器。双通道快速傅里叶变换分析仪CF-5220Z的指标已列于表2。根据乐器厂的要求，初始木料被切割成36块，用于制作9把月琴，月琴共鸣板素材振动特性主要指标见表3。

本研究中，采用弯曲振动试验来确定共鸣板板用木材的声学振动特性。纵向的试样在两端用2个泡沫支架支撑着。高灵敏度、宽频带、低噪声的麦克风被放置在试样的一端。通过1个轴、1个旋转的刀片在试样的另一端敲击试样。声音信号由传声器收集，然后放大、过滤，采用双通道快速FFT分析仪获得共振频率，进而对其弹性模量（E）、动态弹性模量（E/ρ，ρ为声板密度）、声辐射阻尼系数（R）、弹性模量和剪切模量比（E/G）和声阻抗（ω），以及损耗角正切（tan δ）和声转化率（ACE）等参数计算。使用式（1）估计共鸣板的动态弹性模量（GPa）。

E=（48π^2 L^4 ρf^2）/（β_n^4 h^2 ）。 （1）

式中：L为乐器声板的长度，m；ρ为声板密度，kg·m-3；f为声板共振频率，Hz；β_n为木材边界条件的相对常数；h为声板厚度，cm。

损耗角正切（tanδ）是一个重要参数，其定义为振动周期内热损耗能量与介质存储能量之比。计算公式为

tanδ=δ/π=1/Q。 （2）

式中：δ为对数衰减率；Q为品质常数。损耗角正切的值反映了乐音的饱满性，其值与振动效率呈负相关，与乐音衰减速度呈正相关。

声阻抗（ω）和声辐射阻尼系数（R）是2个重要声学参数，在数学上表示为式（3）和式（4）。

ω=ρv=√ρE。 （3）

R=v/ρ=√（E/ρ^3 ）。 （4）

式中：ρ为样品木材的密度，kg·m-3；v为表面波速（纵向），m/s。

另一个参数是声转化率（ACE，式中记为ACE）， 其计算公式为

A_CE=√（E⁄ρ）/（tanδ×ρ）。 （5）

其数值与共鸣板发音效果的稳定性密切相关。除上述7个共鸣板振动特性参数外，制作共鸣板木料的含水率、密度、生长年限、生长轮宽度、泊松比、硬度以及共鸣板的表面光滑度共计14个参数被用于预测由共鸣板制作的月琴的声学品质。

前期对共鸣板素材、共鸣面板、共鸣构件、木质共鸣体、乐器成品声学品质，即整个月琴生产过程各阶段木材振动特性进行了详细的相关性研究［17］，研究结果显示，月琴共鸣板素材振动特性、共鸣面板振动特性、共鸣构件振动特性、木质共鸣体振动特性、乐器成品声学品质两两特性之间高度相关。通过月琴生产过程各阶段相关性分析，验证了共鸣板素材振动特性与乐器成品声学品质之间具有较高相关性，符合乐器生产加工中的实际情况，因此构建月琴乐器共鸣板素材振动特性的声学品质预测模型是可行的。

在试验中，36块共鸣板被用于测试，为了保证试验的准确性，排除环境等其他因素的影响，对每块共鸣板进行5次测定。因此，总共收集了180组数据。由经验丰富的音乐专家和月琴演奏家将乐器产品的声学质量。根据声音响度、动态范围、声音长度和音色等指标分为9个等级进行客观评价，然后在每个等级中，随机抽取15组数据，共计135组用于预测模型的训练。训练完成后，取剩余45组未使用的数据用于验证，用这36块共鸣板做了9把月琴。

1.2 主成分分析

通过对共鸣板素材参数进行测量，发现声辐射阻尼系数、声阻抗等参数极有可能与这些共鸣板素材经过后期加工制作出的月琴成品的声学品质有关，但过多的变量会增加计算量和问题的复杂性。考虑到共鸣板特性参数反映的信息在一定程度上有重叠和冗余，使用主成分分析［18-19］，将14个参数转化为较少数量的综合指标，实现数据降维。其计算过程如下。

记m_1，m_2，…，m_p为原共鸣板素材参数，x_1，x_2，…，x_m （m≤p）为新变量指标。假定采集到了n组样本，则样本数据构成一个M矩阵。

M=[（m_11&…&m_1p@⋮&⋱&⋮@m_n1&…&m_np ）]=[m_1…m_p]。 （6）

首先对矩阵元素进行归一化

z_ij=（m_ij-¯m_j）/s_j ，i=1，2，…，n;j=1，2，…，p。 （7）

其中，¯（m_j ）=（∑_（i=1）^n▒〖⋅m_ij 〗）/n，s_j^2=（∑_（i=1）^n▒〖（m_ij-¯m_j ）^2 〗）/（n-1），得归一化矩阵Z。

Z=[（Z_1^T@Z_2^T@⋮@Z_n^T ）]=[（z_11&…&z_1p@⋮&⋱&⋮@z_n1&…&z_np ）]。 （8）

而后，求Z的相关矩阵R

R=[r_ij ]_（p×p）=（Z^T Z）/（n-1）。 （9）

其中，r_ij=（∑_（k=1）^n▒〖Z_ik Z_kj 〗）/（n-1），i、 j=1，2，…，p。

随后求解R的特征方程

Rb_j=λ_j b_j^0。 （10）

式中：λ_j （j=1，2，…，p）是矩阵R的p个特征值；b_j^0 为相应的特征向量。

对特征向量进行归一化处理，b_j^0=b_j^0/‖b_j^0 ‖为长度归一化的特征向量。

最后，求取主成分分量（U_j）

U_j=Zb_j^0，j=1，2，…，m。 （11）

式中：m表示主成分分量的个数，选择其数值的通常做法是取特征值λ_j大于1，或者令累计贡献率大于95%。

1.3 GRNN回归模型

以共鸣板素材的振动特性参数为模型输入，以这些共鸣板素材制作的月琴，其声学品质等级作为输出建立广义回归神经网络模型（GRNN）。记GRNN输入矢量为x=[|x_1 |，|x_2 |，…，|x_m |]，其中，每一项代表一个共鸣板素材的振动特性参数，总计有m个参数。输入矢量依次与GRNN的输入层、模式层、求和层和输出层［20-21］进行代数运算，得出声学品质预测结果。

输入层只起到对输入矢量的读取作用，不进行计算，其神经元个数为m。在模式层中，输入矢量的第i个元素x_i的计算规则为

T_i=e^（-（（x|-|x_i ）^T （x|-|x_i ））/（2σ^2 ）） 。i=1，2，…，m。 （12）

式中：T_i为模式层第i个神经元的输出；x_i为全体样本第i个振动特性参数构成的矢量；σ为平滑系数，是网络优化的目标参数。

求和层包括2种计算规则，分别为

S_D=∑_（i=1）^n▒T_i 。 （13）

S_N=∑_（i=1）^n▒〖（y_i |T_i）〗。 （14）

式中：S_D和S_N是分别表示求和层2种神经元的输出；y_i为第i个样本的声学品质标定结果。最后，输出层神经元的运算过程为

y ̂=S_N/S_D 。 （15）

式中，y ̂表示模型的声学品质预测结果。

最后，基于交叉验证［22］的方法训练模型，并使用遗传算法［23-24］对网络目标参数（σ）进行优化。

2 结果与分析

2.1 样本数据的降维处理

指标的选择和相关标准的建立是基于乐器产品等级预测的重要部分。邀请了中国音乐学院的两位从事民族乐器鉴定的教授对月琴品质的等级进行鉴定。根据中国国家标准GB/T 16463—1996［25］广播节目音质的主观评价方法、技术指标，以及中国国家质量标准CSBTS，（中国国家质量技术监督局）采用的主观评价和等级标准中的统计方法，将9把月琴分为1—9级，其中1—3级为一级， 4—6级为二级，7—9级为三级。

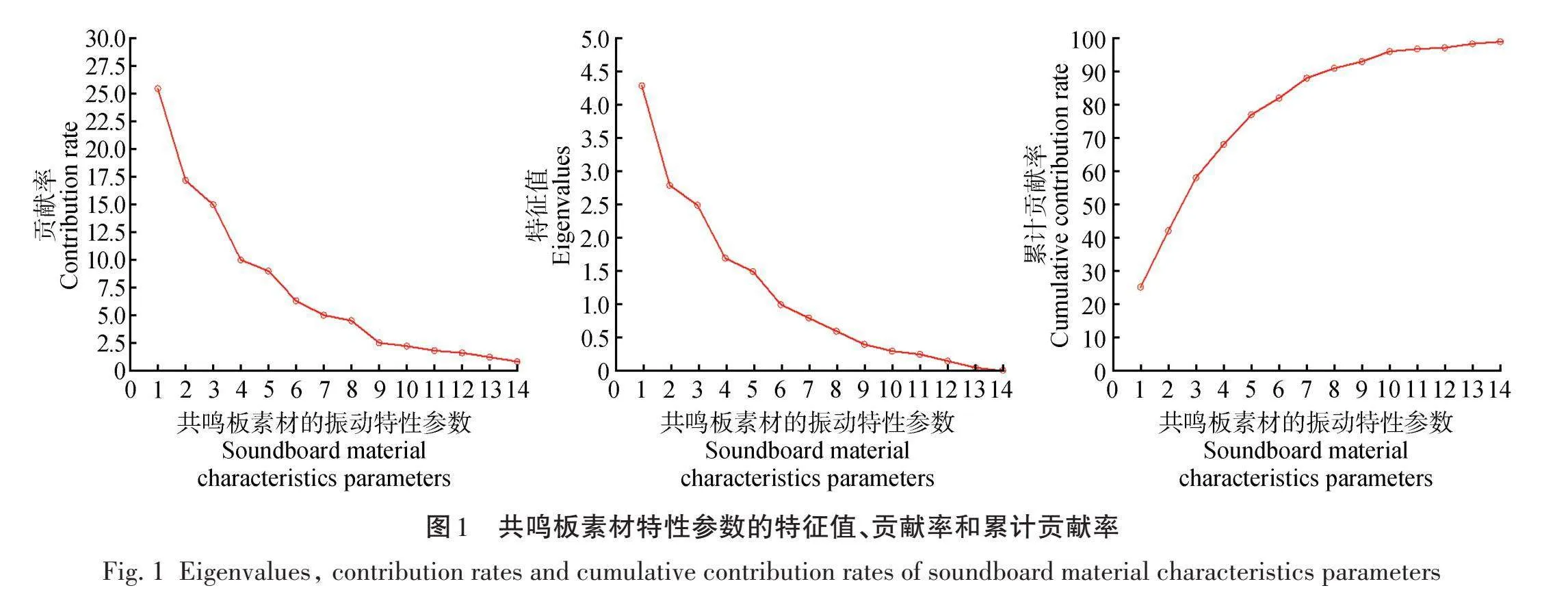
选取与月琴声学质量相关的共鸣板14个特征参数构建模型，评价月琴声学品质。使用主成分分析进行特征参数降维，去除冗余信息。

由图1可知，前6个参数的特征值大于1，其分别为动态弹性模量E/ρ、剪切模量比E/G、声辐射阻尼系数R、声阻抗ω、损耗角正切（tanδ）和声转化率（ACE），前6个参数共提供了82.41%的累计贡献率。前10个参数（还包括弹性模量、含水率、密度和生长年限）提供了96.07%的累计贡献率，大于95%。因此，按照2种方法可以分别取式（12）中的m=6或 m=10，此外，本研究还设置了m=14作为参照。

2.2 模型的构建与训练

按照不同的m建立GRNN模型。GRNN是一种径向基网络，前一层网络节点的输出线性组合成为下一层网络的输入，经过输入层、模式层、求和层、输出层节点依次按照式（13）—式（16）运算后得到预测结果。模型的输入矢量x的维度m，输出值为网络预测的月琴声学品质等级。训练结果如图2（a）、图2（c）、图2（e）所示。

2.3 模型预测结果与评估

试验环境为Matlab2017a，GRNN的输入层、模式层、求和层和输出层的节点数都设置为m、12、12、1；180组试验数据分为2部分，其中135组用于训练模型，45组用于验证分类结果。

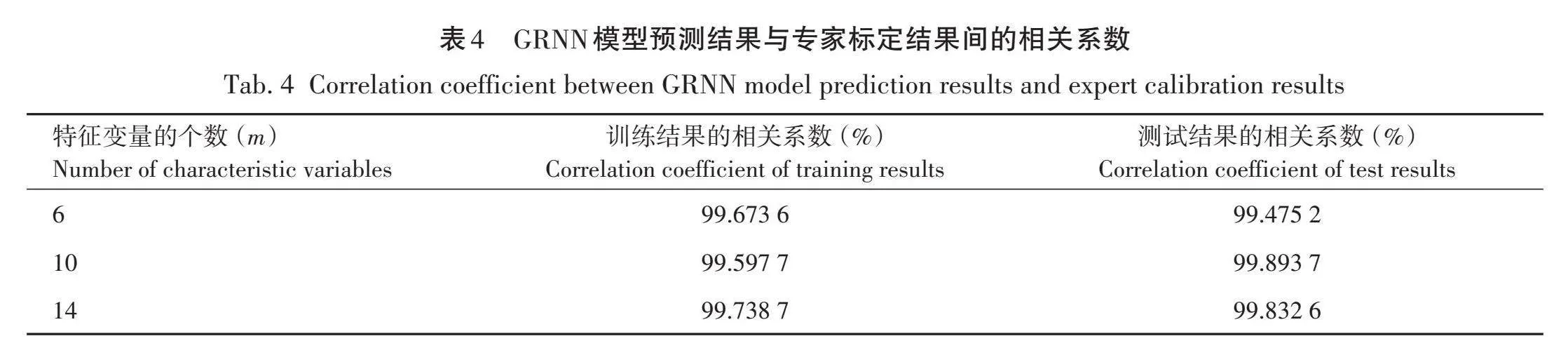
表4为使用GRNN模型在m=6，m=10，m=14时，在训练样本和测试样本上的预测结果与实际样本间的相关系数。

由图2（c）、图2（d）仿真结果表明，尽管GRNN模型在m分别为14、10、6时，预测的月琴声学品质等级结果与实际的拟合度较高，但均存在一定的波纹，说明本研究方法受到一定的限制，m=14时，纹波最小，说明最稳定，这也表明在使用PCA对数据降维时，会对模型稳定性产生微弱的影响。此外，表5为使用模型预测等级和实际等级的比较给出错误样本的数量，当误差大于±0.1时被归类为假。按照这一标准，GRNN模型在m=14时，用于训练的145个月琴共鸣板素材样本中，有10个样本是错误的，计算出GRNN模型预测的等级分类训练的准确率为93.74%。同理可得，模型在m=10以及m=6时，在训练样本上的准确率分别为91.03%和90.34%。在用于测试的45个月琴共鸣板样本上，GRNN模型在m分别为14、10、6的准确率分别为91.41%、84.44%和86.67%。结合表4、表5共同可得，使用GRNN模型以制作月琴的共鸣板素材特性预测月琴声学品质等级，可以达到较高精度。使用PCA方法保留完整共鸣板素材特性时（m=14），GRNN模型取得最佳效果。对于m=6以及m=10的情况，预测结果差别不大，均具有较高水准。这说明仅使用6个共鸣板素材特性就可以达到良好的月琴声学品质预测效果。

3 结论

本研究测量了制作月琴的共鸣板素材的振动特性，预测这些共鸣板制备成月琴的声学质量。使用主成分分析方法对测得的14个共鸣板素材特征参数降维，明确了影响制备月琴的最主要共鸣板素材振动参数（动态弹性模量、声辐射阻尼系数、剪切模量比、声阻抗、损耗角正切和声转化率）。基于广义回归神经网络构建了月琴声学质量预测模型，对比不同的共鸣板素材参数主成分的预测结果。试验表明，在主成分特征参数维度为6时，即可取得良好的预测结果。m为14、10、6时，模型预测的准确率可达到91.41%、84.44%和86.67%。该项研究将会对我国民族乐器材料的科学选取奠定理论基础。

【参 考 文 献】

［1］ DAMODARAN A，LESSARD L，SURESH B A.An overview of fibre-reinforced composites for musical instrument soundboards［J］.Acoustics Australia，2015，43（1）：117-122.

［2］ DUERINCK T，VERBERKMOES G，FRITZ C，et al.Listener evaluations of violins made from composites［J］.The Journal of the Acoustical Society of America，2020，147（4）：2647-2655.

［3］ LIU F，WANG K，LANG C，et al.Mechanical and acoustic emission properties of vegetable fiber-reinforced epoxy composites for percussion instrument drums［J］.Polymer Composites，2021，42（6）：2864-2871.

［4］ SHIRMOHAMMADI M，FAIRCLOTH A，REDMAN A.Determining acoustic and mechanical properties of Australian native hardwood species for guitar fretboard production［J］.European Journal of Wood and Wood Products，2020，78（6）：1161-1171.

［5］ NORIMOTO M，TANAKA F，OHOGAMA T，et al.Specific dynamic Young′s modulus and internal friction of wood in the longitudinal direction［J］.Wood Research and Technical Notes，1986，22：53-65.

［6］ MATSUNAGA M，SUGIYAMA M，MINATO K，et al.Physical and mechanical properties required for violin bow materials［J］.Holzforschung-International Journal of the Biology，Chemistry，Physics and Technology of Wood，1996，50（6）：511-517.

［7］ YOSHITAKA K，OKANO T，OHTA M.Effect of annual ring widths on structural and vibrational properties of wood［J］.Journal of the Japan Wood Research Society，1997，43（8）：634-641.

［8］ YOSHITAKA K，OKANO T，OHTA M.Vibrational properties of Sitka spruce heat-treated in nitrogen gas［J］.Journal of Wood Science，1998，44（1）：73-77.

［9］ BUKSNOWITZ C，TEISCHINGER A，MULLER U，et al.Resonance wood ［Picea abies （L.） Karst.］-evaluation and prediction of violin makers'quality-grading［J］.The Journal of the Acoustical Society of America，2007，121（4）：2384-2395.

［10］ TRAORE B，BRANCHERIAU L，PERRE P，et al.Acoustic quality of vène wood （Pterocarpus erinaceus Poir.） for xylophone instrument manufacture in Mali［J］.Annals of Forest Science，2010，67（8）：815-815.

［11］ WONG T H，NG J S，AFIF M，et al.Classification of sape soundboard wood quality by employing machine learning［A］.Proceedings of TEPEN 2022［C］.Springer，Cham，2023：32-42.

［12］ LIU L.Lute acoustic quality evaluation and note recognition based on the softmax regression BP neural network［J］.Mathematical Problems in Engineering，2022：e1978746.

［13］ 杨扬，刘镇波，刘一星，等.应用随机森林算法检测琵琶共鸣板振动特性及声学品质评价［J］.东北林业大学学报，2019，47（8）：66–69.

YANG Y，LIU Z B，LIU Y X，et al.Lute sound board vibration performance acoustics quality model by random forest method［J］.Journal of Northeast Forestry University，2019，47（8）：66-69.

［14］ HUANG Y，MENG S，LI X，et al.A classification method for wood vibration signals of Chinese musical instruments based on GMM and SVM［J］.Traitement Du Signal，2018，35（2）：137-151.

［15］ KAFFASH C N，GHOLAMI A，ABDOLLADZADEH B A.Road accident risk prediction using generalized regression neural network optimized with self-organizing map［J］.Neural Computing and Applications，2022，34（11）：8511-8524.

［16］ SRIDHARAN M，SHENGAGARAJ S.Application of generalized regression neural network in predicting the thermal performance of solar flat plate collector systems［J］.Journal of Thermal Science and Engineering Applications，2020，13（2）：21-23.

［17］ 杨扬.基于泡桐木材振动特性的民族乐器声学品质预测模型研究［D］.哈尔滨：东北林业大学，2017.

YANG Y.Research on vibration property of Paulownia wood for the national musical instrument forecast model［J］.Harbin：Northeast Forestry University，2017.

［18］ 周婷，汪炎，邹俊，等.基于PCA和SVM的遥感影像水体提取方法及验证［J］.水资源保护，2023，39（2）：180-189.

ZHOU T，WANG Y，ZOU J，et al.PCA and SVM-based algorithm of water area extraction from remote sensing images and its verification［J］.Water Resources Protection，2023，39（2）：180-189.

［19］ 冯志亮，肖涵麒，任文凤，等.基于主成分分析的海鸥优化支持向量机变压器故障诊断［J］.中国测试，2023，49（2）：99-105.

FENG Z L，XIAO H Q，REN W F，et al.Transformer fault diagnosis based on principal component analysis and seagull optimization support vector machine［J］.China Measurement & Test，2023，49（2）：99-105.

［20］ 邹红波，宋璐，张馨煜，等.基于PSO-GRNN和D-S证据理论的电网分区故障诊断［J］.智慧电力，2023，51（3）：25-30，45.

ZOU H B，SONG L，ZHANG X Y，et al.Divisional fault diagnosis of power grids based on PSO-GRNN and D-S evidence theory［J］.Smart Power，2023，51（3）：25-30，45.

［21］ 夏翔，李贤良，潘华，等.基于广义回归神经网络的光纤光栅传感器解调技术研究［J］.电测与仪表，1-7.

XIA X，LI X L，PAN H，et al.Research on demodulation technology of fiber bragg grating sensor based on generalized regression neural network［J］.Electrical Measurement & Instrumentation，1-7.

［22］ 汪学清，刘爽，李秋燕，等.基于K折交叉验证的SVM隧道围岩分级判别［J］.矿冶工程，2021，41（6）：126-128，133.

WANG X Q，bc5ac2e94aa20c2fae4c5ccef812044b2f0016551656cd04b7f45b3c6e8585cbLIU S，LI Q Y，et al.Classification and discrimination of surrounding rock of tunnel based on SVM of K-fold cross validation［J］.Mining and Metallurgical Engineering，2021，41（6）：126-128，133.

［23］ 阮斯佳，赵欣欣，王燕，等.基于响应面和人工神经网络-遗传算法优化鲜切萝卜光动力杀菌工艺［J］.南京农业大学学报，2023，46（6）：1196-1205.

RUAN S J，ZHAO X X，WANG Y，et al.Optimization of photodynamic pasteurization process of fresh-cut radish based on response surface methodology and artificialneural network-genetic algorithm［J］.Journal of Nanjing Agricultural University，2023，46（6）：1196-1205.

［24］ 胡喆馨，卜凡亮，丁丹丹.基于GAPSO优化的神经网络无线信道参数预测［J］.无线电工程，2023，53（12）：2944-2950.

HU Z X，BU F L，DING D D.Wireless channel parameter prediction by BPNN based on GAPSO optimization［J］.Radio Engineering，2023，53（12）：2944-2950.

［25］ 中华人民共和国技术监督局.GB/T 16463—1996，广播节目声音质量主观评价方法和技术指标要求［S］.北京：中国标准出版社，1996.

The Technical Supervision Bureau of the People's Republic of China.GB/T 16463—1996，Subjective evaluation methods and technical requirements for sound quality of radio programs［S］.Beijing：Standards Press of China，1996.