并联天线机构尺度优化分析与验证

摘" 要： 天线机构尺度优化设计是天线样机研制和工程应用的重要环节，将承载能力与驱动分支运动范围作为并联天线机构尺度优化目标，基于参数化设计模块开展尺度优化分析.首先对并联天线机构结构进行描述，建立了机构运动学模型；然后根据天线工作要求定义机构的设计变量、目标函数和约束条件，利用ADAMS优化设计模块建立机构的参数化模型；其次研究设计变量对目标函数的影响，得到综合性能优异的机构尺度参数；最后根据尺度优化结果研制天线样机并开展实验研究，实验结果表明，天线样机可实现预期运动且未出现干涉现象，其结果为并联天线机构的优化设计和样机研制提供参考.

关键词： 并联天线;参数化建模;尺度优化;样机实验

中图分类号：TH112""" 文献标志码：A""""" 文章编号：1673-4807（2024）01-055-07

DOI：10.20061/j.issn.1673-4807.2024.01.009

收稿日期： 2022-03-18""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（51905228）；国家重点研发计划项目（2018YFC0309100）；江苏省自然科学基金青年基金项目（BK20220649）；江苏省高等学校基础科学（自然科学）研究面上项目（23KJB460010）；江苏省研究生科研与实践创新计划项目（SJCX23_2143）

作者简介： 张国兴（1990—），男，博士，讲师，研究方向为机器人机构理论与应用.E-mail：gxzhang@just.edu.cn

引文格式： 张国兴，夏新露，郭金伟，等.并联天线机构尺度优化分析与验证［J］.江苏科技大学学报（自然科学版），2024，38（1）：55-61.DOI：10.20061/j.issn.1673-4807.2024.01.009.

Dimension optimization analysis and verificationof parallel antenna mechanism

ZHANG Guoxing1， XIA Xinlu1， GUO Jinwei1， WANG Zhibin2， WANG Jia1， LI Chong1

（1.School of Mechanical Engineering， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

（2.708th Research Institate of China State Shipbuilding Corporation， Shanghai 200011，China）

Abstract：The dimension optimization design of antenna mechanism is an important procedure in the development and engineering application of antennae. The bearing capacity and the motion range of the actuation branch are proposed as the dimension optimization objectives of the parallel antenna mechanism. The dimension optimization analysis is carried out based on the parametric design module. Firstly， the structure of the parallel antenna mechanism is described， and the kinematic model of the mechanism is established. Then the design variables， objective functions and constraints of the mechanism are defined according to the working requirements of the antenna. The parametric model of the mechanism is established by using the optimization design module of Adams. Secondly， the influence of design variables on the objective function is studied. The mechanism scale parameters with excellent comprehensive performance are obtained. Finally， according to the dimension optimization results， the antenna prototype is developed and experimental research is carried out. The experimental results show that the antenna prototype can achieve the expected motion without interference. The research work provides a reference for the optimal design and prototype development of parallel antenna mechanism.

Key words：parallel antenna， parametric modeling， dimension optimization， prototype experiment

天线是无线通信系统的关键部件，伴随天线应用领域和应用环境的持续拓展，对天线系统综合性能的要求不断提升，亟待探索天线系统高效的设计和优化方法［1］.相对传统串联天线，并联天线机构具有承载能力强和重复定位精度高的优势［2］.文献［3］提出一种利用并联机构支撑天线完成其有效的旋转追踪的方案，有效地改善了天线结构上的不足.文献［4］建立了新型天线机构的动力学模型，求解机构的速度、加速度与关节驱动力矩.文献［5］研究了用于星间链路天线的两转动自由度并联机构的构型综合问题，提出了两种新型的两转动并联天线.文献［6］提出一种的并联式车载天线机构，分析了基座运动对天线驱动力矩的影响.文献［7］将三自由度并联机构应用于天线领域，设计了并联天线的结构.文献［8］提出一种混联式天线机构，建立了机构的运动学模型，完成了运动特性仿真和样机实验.文献［9］设计了一种三自由度并联天线机构，通过实验验证了天线转动能力.文献［10］设计了一种新型可展天线机构，分析了天线机构的模块化组合原理及性能.文献［11］提出采用冗余驱动提高并联指向机构的定位精度.文献［12］提出了一种用于空间天线指向的二自由度并联天线系统，通过迭代优化设计研究指向范围与结构刚度的关系.文献［13］利用遗传算法对并联机构进行了尺度优化，获得了具有良好运动性能的机构尺寸参数.文献［14］基于ADAMS软件建立驱动经济性与承载能力两个优化目标，研究了一种混联转台机构的尺度优化问题.文献［15］对并联平台进行参数化建模，分析了机构各个尺度参数对机构整体性能的影响，得到一组优化后的机构尺寸参数.

文中以三自由度并联天线机构为研究对象，面向天线工程应用实际需求，提出针对驱动参数和运动范围指标的优化设计指标，开展并联天线机构优化设计与实验研究.

1" 并联天线机构构型分析

如图1，并联天线机构由动平台、定平台和3条支链构成，3个支链与定平台和动平台均通过转动副连接，将与定平台连接的转动副驱动转角记为βi（1，2，3），定平台和动平台均为等边三角形.在定平台与动平台上分别建立坐标系O－xyz和坐标系C－xyz，Ox轴方向与OP1一致，Oz轴垂直于定平台且向上为正，Cx轴与CQ1一致，Cz轴垂直于动平台且向上为正.定坐标系与动坐标系原点矢量OC的为相对距离，记为r，OC与定坐标系z轴的夹角为κ，定坐标系与动坐标系z轴的夹角为俯仰角，记为δ，动坐标系Cz轴在平面xoy的投影与定系Cx轴的夹角为方位角，记为ζ.R为定平台和动平台外接圆半径，L为连杆长度，H为上平台距下平台的初始高度.

初始位姿下并联天线机构转动副Pi（i=1，2，3）在定坐标系O-xyz中的坐标矢量分别为：

OP1=［R，0，0］T

OP2=［－R/2，3R/2，0］T

OP3=［－R/2，－3R/2，0］T（1）

并联天线机构球副Gi（i=1，2，3）在定坐标系O－xyz中的坐标矢量简化表示为：

OG1=［K，0，H/2］T

OG2=［K/2，－3K/2，H/2］T

OG3=［－K/2，－3K/2，H/2］T（2）

式中：K=R+（L/2）2－（H/2）2

并联天线机构转动副Qi在定坐标系O－xyz中的坐标矢量分别为：

OQ1=［R，0，H］T

OQ2=［－R/2，3R/2，H］T

OQ3=［－R/2，－3R/2，H］T（3）

给定机构运动平台的位置矩阵Or和姿态矩阵ORC，根据天线机构结构特点，分支的闭环矢量方程为：

OOPi+OPiGi+OGiQi=Or+ORCCCiQi（4）

根据机构闭环矢量方程，式（4）表示为：

OGiQi=Or+ORCCCiQi－OOPi－OPiGi（5）

动坐标系原点在定坐标系下位置矢量为Or=［rsin κcos ζ，rsin κsin ζ，rcos κ］T，动坐标系相对于定坐标系的姿态矩阵ORC为：

ORC=s2ζvδ+cδ－sζcζvδcζsδ－sζcζvδc2ζvδ+cδsζsδ－cζsδ－sζsδcδ（6）

根据机构的杆长约束条件|OGiQi|=L，可以得到：

（xGi-xQi）2+（yGi-yQi）2+（zGi-zQi）2=L2（7）

通过式（7）即可得到并联天线机构输入与输出的关系.

2" 机构模型参数化

2.1" 结构参数化建模

基于ADAMS软件建立机构的参数化模型，对机构的关键尺度进行优化设计.机构的结构尺寸主要由连杆长度L、定平台半径RO、动平台半径RC、动/定平台中心距r4组参数决定，初步确定机构的设计参数，如表1.

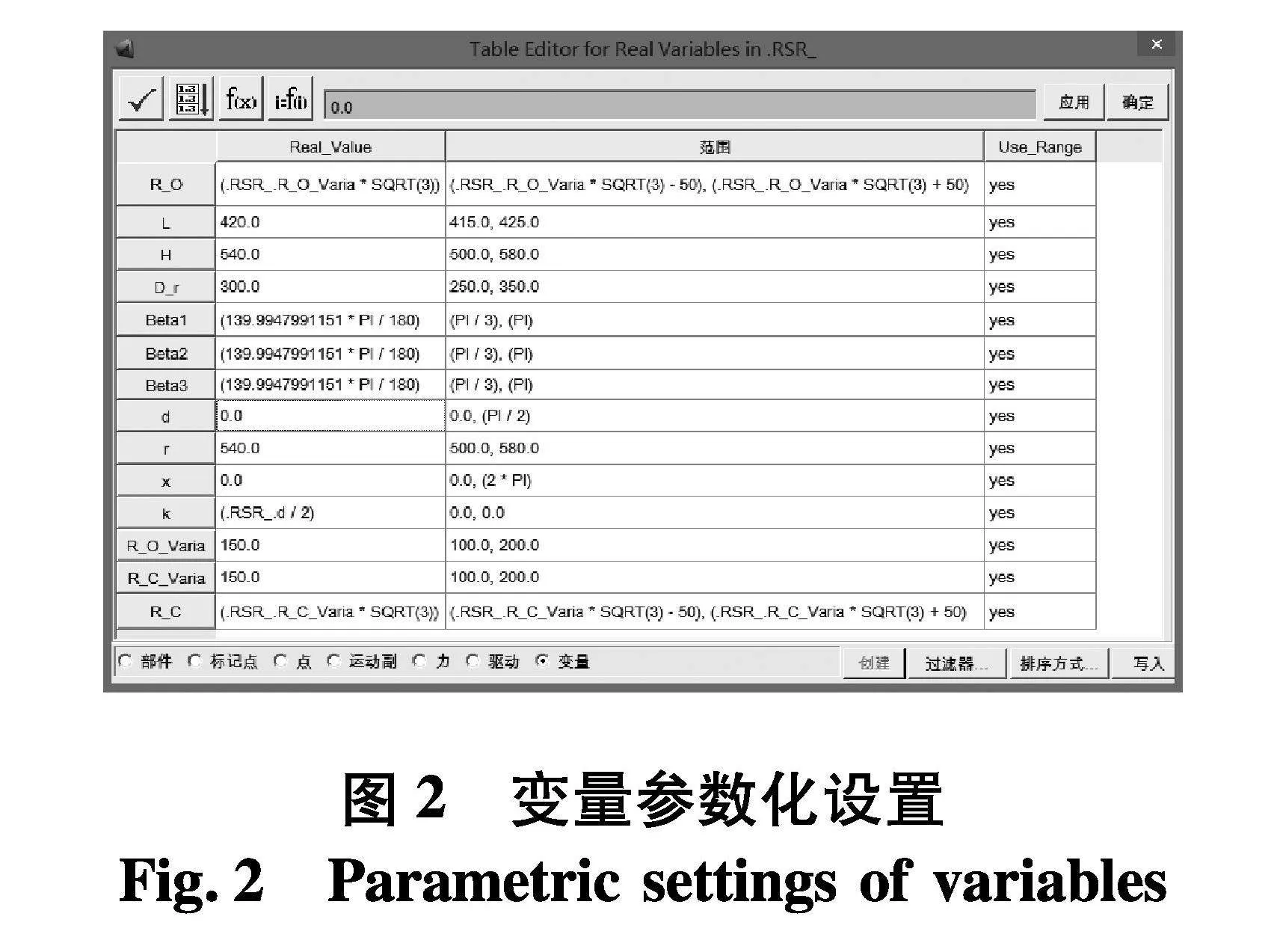
在ADAMS参数化分析模块中创建11个标记点，分别为定平台中心点、动平台中心点和9个铰链点，创建的标记点即可表征并联天线机构的空间结构.根据几何特征完成11个标记点的参数化方程.定义的设计变量还包括杆长参数L，初始高度H，初始转角Beta1、Beta2、Beta3，方位角x，俯仰角d，定平台半径R_O_Varia，动平台半径R_C_Varia等，变量参数化设置界面和数值如图2.

依据并联天线机构的结构约束关系和设计变量参考值，参数化处理后的各个标记点如图3.

采用线条将参数化特征点进行连接，并联天线机构参数化模型如图4.

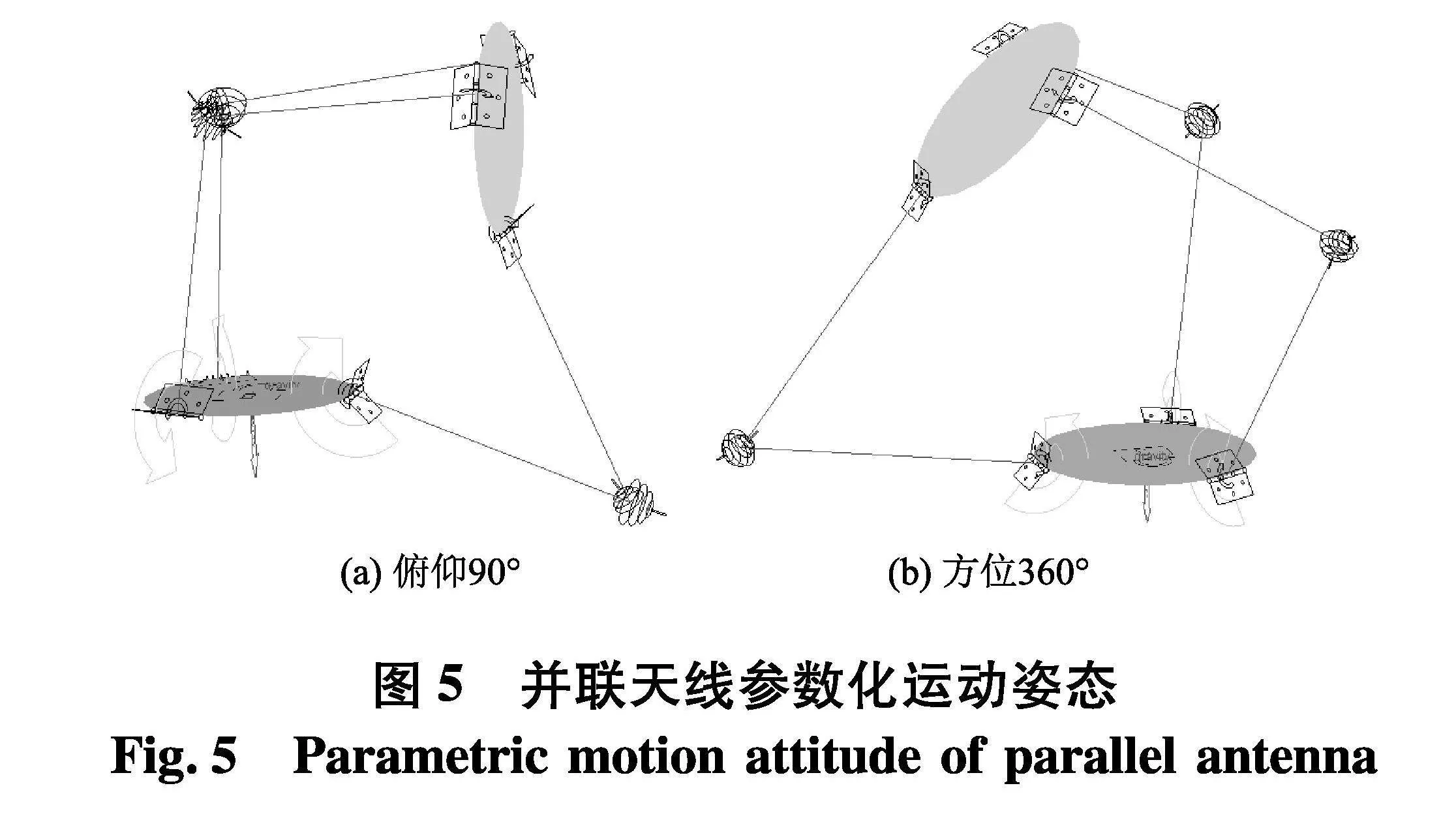
根据天线机构运动特点规划天线机构参数化模型轨迹，用以寻找特点轨迹范围下设计参数的最优值.选取天线机构俯仰90°和方位360°两组典型运行轨迹，两组轨迹下机构参数化模型如图5.

2.2" 驱动参数化

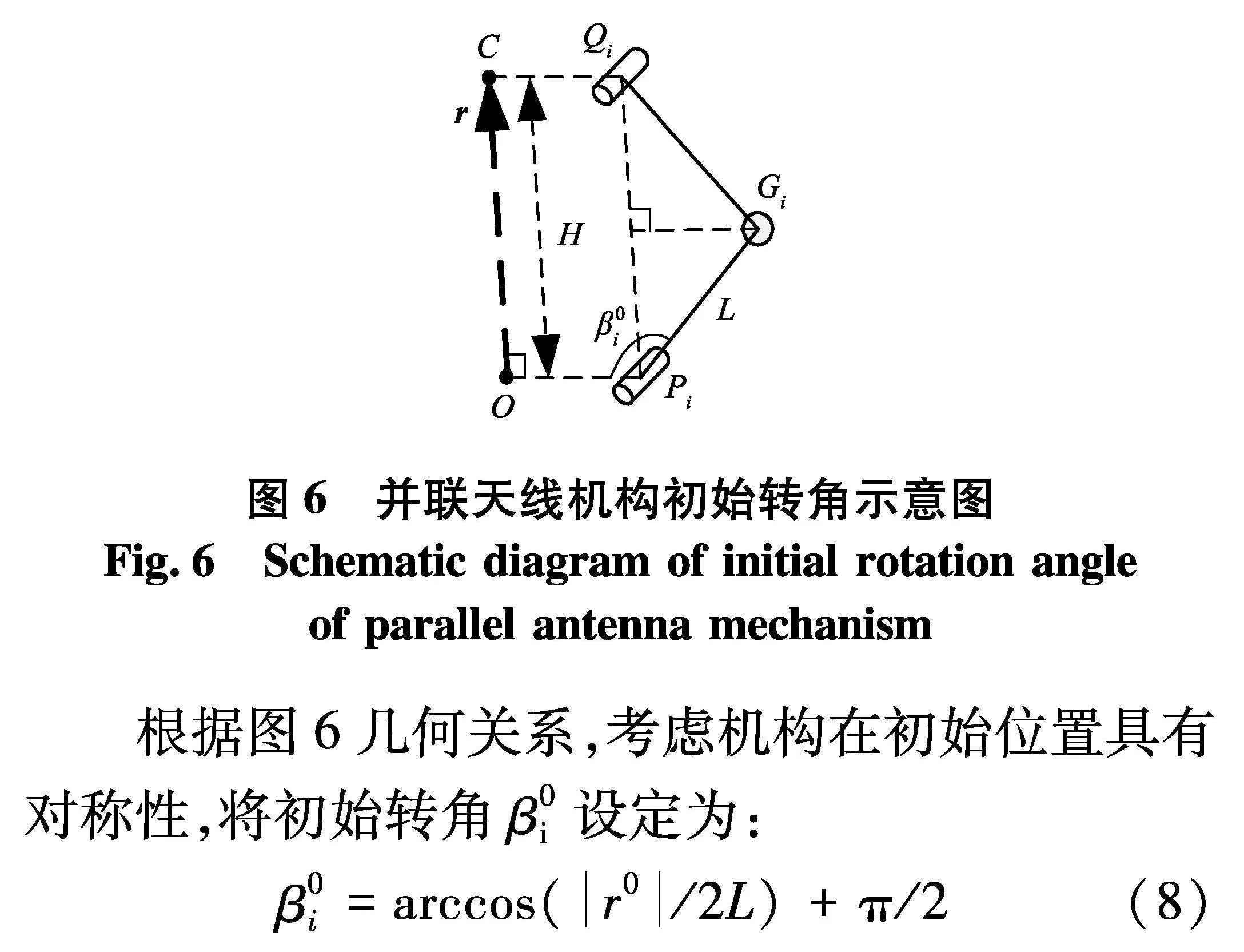
根据天线机构俯仰90°的典型运行轨迹特点，需要给定并联天线机构的初始位置，初始位置主要由机构的驱动初始转角β0i（i=1，2，3）和初始高度H=r0表示，如图6.

根据图6几何关系，考虑机构在初始位置具有对称性，将初始转角β0i设定为：

β0i=arccos（r0/2L）+π/2（8）

由式（8）可知，初始转角为连杆长度L和动/定平台中心距r0的函数.参数化分析过程中通过修改L和r0的值，即可实现初始转角的参数化.

依据天线机构运动学模型，将机构3个驱动参数设置成参数化形式.在参数化分析模型的驱动处分别写入驱动的参数化表达式，驱动的3组表达式Motion1、Motion2、Motion3分别为：

Motion1=step（time，0，0，5，if（X1：DV_Motion1a，DV_Motion1b，DV_Motion1b）Motion2=step（time，0，0，5，if（X2：DV_Motion2a，DV_Motion2b，DV_Motion2b）Motion3=step（time，0，0，5，if（X3：DV_Motion3a，DV_Motion3b，DV_Motion3b）（9）

完成驱动的参数化建模，可将驱动定义为结构变量的函数，实现参数化分析过程中驱动函数的便捷调整，提高参数化分析的便捷性.

3" 机构尺度优化

驱动力矩大小关系到伺服电机选型，将机构承载能力作为衡量天线性能的一项优化指标；考虑机构完成相同轨迹运动，分支运动范围尽可能小，将分支运动范围作为另一项优化指标.

3.1" 基于分支驱动力矩指标的优化分析

将重量为30 kg的等效负载置于并联天线机构动平台中心处，根据设定的参数化变量，研究驱动力矩随变量的变化情况.在并联天线机构进行90°俯仰运动时，分别获取单一参数变化情况下3个分支驱动力矩的极大值.在驱动力矩随参数变量变化过程中，驱动力矩的极大值越小，并联天线机构对驱动电机的额定扭矩需求越低.给定优化设计目标函数，在参数化分析模型中设定优化目标，其表达式表示为：

g（x）=min（max（MEA_Torque1，max（MEA_Torque2，MEA_Torque3）））（10）

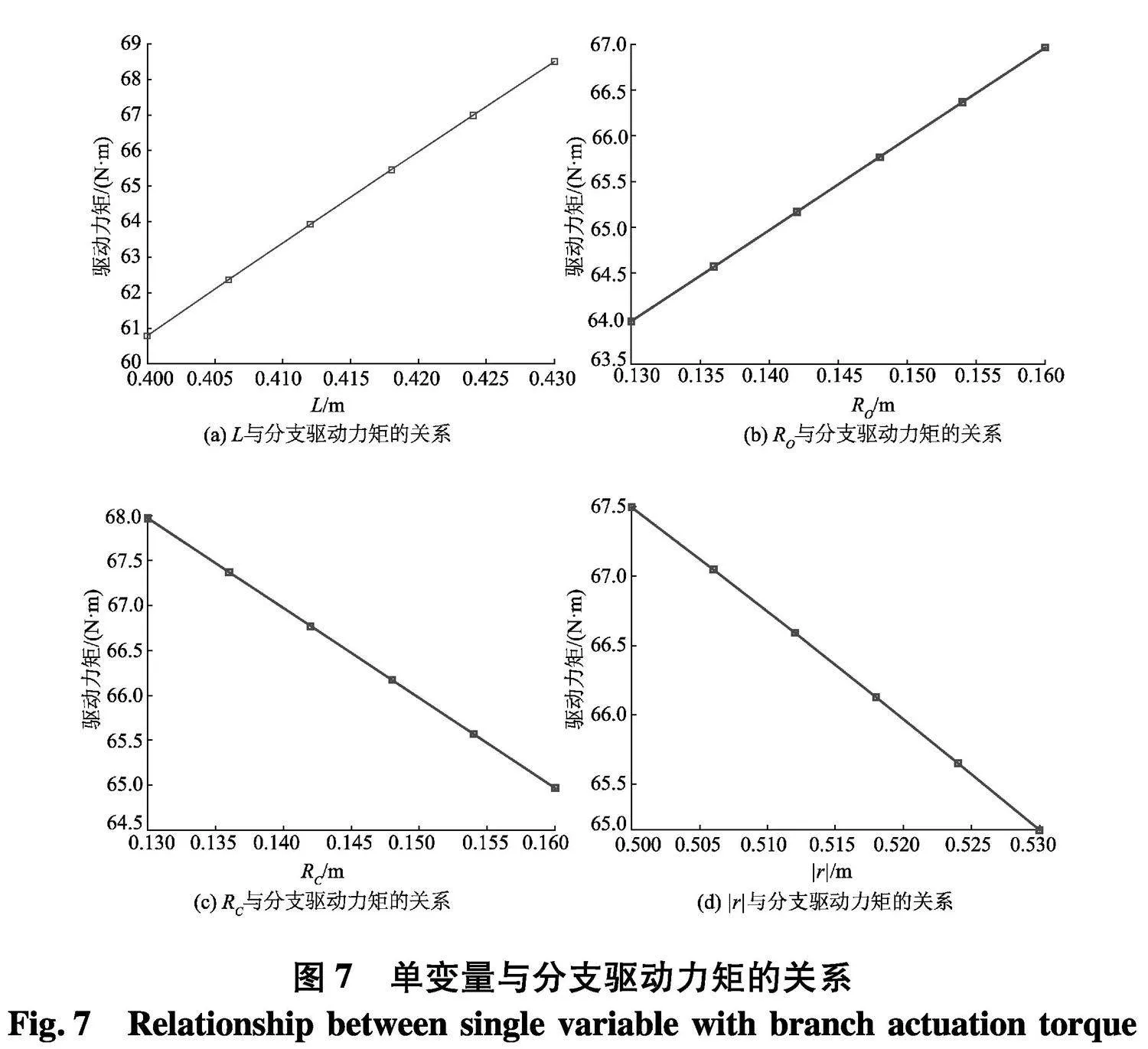
基于参数化分析设计研究模块分别研究单一变量对目标函数的影响情况，对连杆长度L、定平台半径RO、动平台半径RC、动/定平台中心距r4个参数分别进行优化分析，分析结果如图7.

由图7可知，随着连杆长度L的增加，各个分支的驱动力矩极大值增大；随着定平台半径RO的增加，各个分支的驱动力矩极大值增大；随着动平台半径RC的增加，各个分支的驱动力矩极大值减小；随着动/定平台中心距r的增大，各分支驱动力矩极大值减小.

基于参数化分析试验设计功能，给定优化目标和4组设计变量，将设计级别设定为6，即每组设计变量划分为6组数据，共计得到N组构型参数，其中N=64=1 296.基于试验设计模块得到的各组参数与驱动力矩的关系如图8.

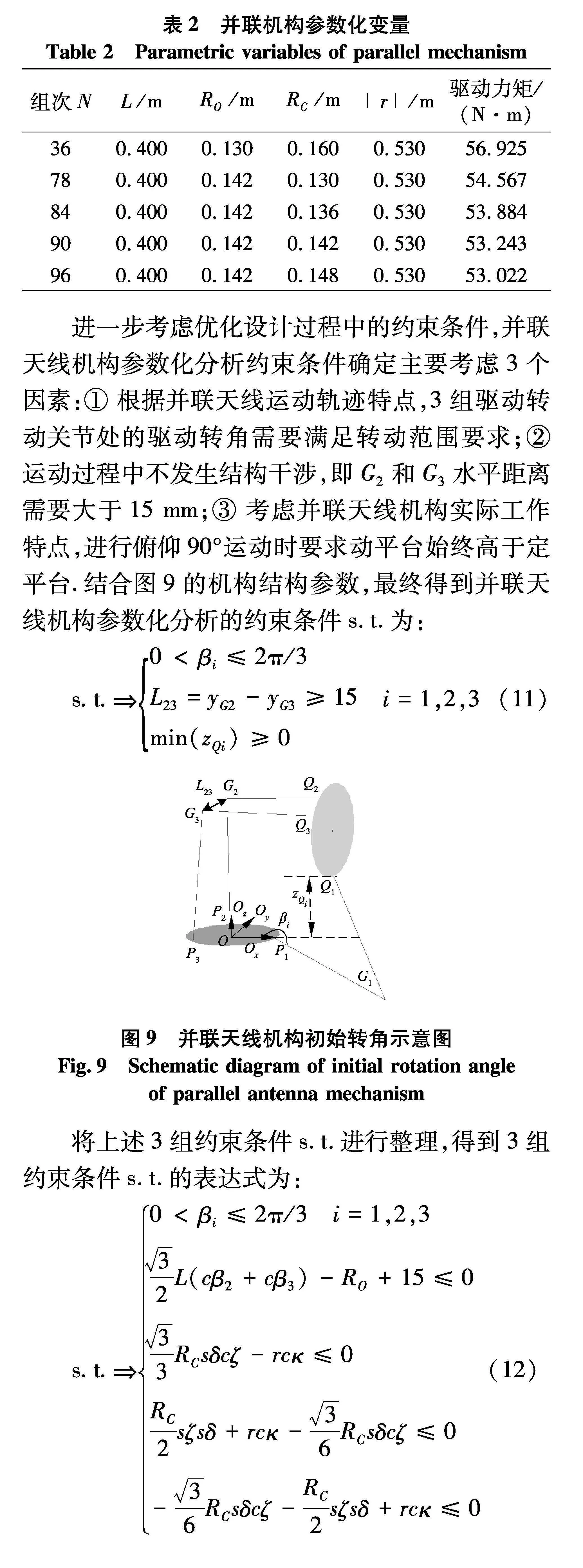
如图8，各分支驱动力矩随着各组设计变量变化呈波动上升，取出分支驱动力矩最大值较小的5组数据，分别为第36、78、84、90和96组驱动力矩值较小，其参数化变量值如表2.

进一步考虑优化设计过程中的约束条件，并联天线机构参数化分析约束条件确定主要考虑3个因素：① 根据并联天线运动轨迹特点，3组驱动转动关节处的驱动转角需要满足转动范围要求；② 运动过程中不发生结构干涉，即G2和G3水平距离需要大于15 mm；③ 考虑并联天线机构实际工作特点，进行俯仰90°运动时要求动平台始终高于定平台.结合图9的机构结构参数，最终得到并联天线机构参数化分析的约束条件s.t.为：

s.t.0lt;βi≤2π/3L23=yG2－yG3≥15min（zQi）≥0" i=1，2，3（11）

将上述3组约束条件s.t.进行整理，得到3组约束条件s.t.的表达式为：

s.t.0lt;βi≤2π/3" i=1，2，332L（cβ2+cβ3）－RO+15≤033RCsδcζ－rcκ≤0RC2sζsδ+rcκ－36RCsδcζ≤0－36RCsδcζ－RC2sζsδ+rcκ≤0（12）

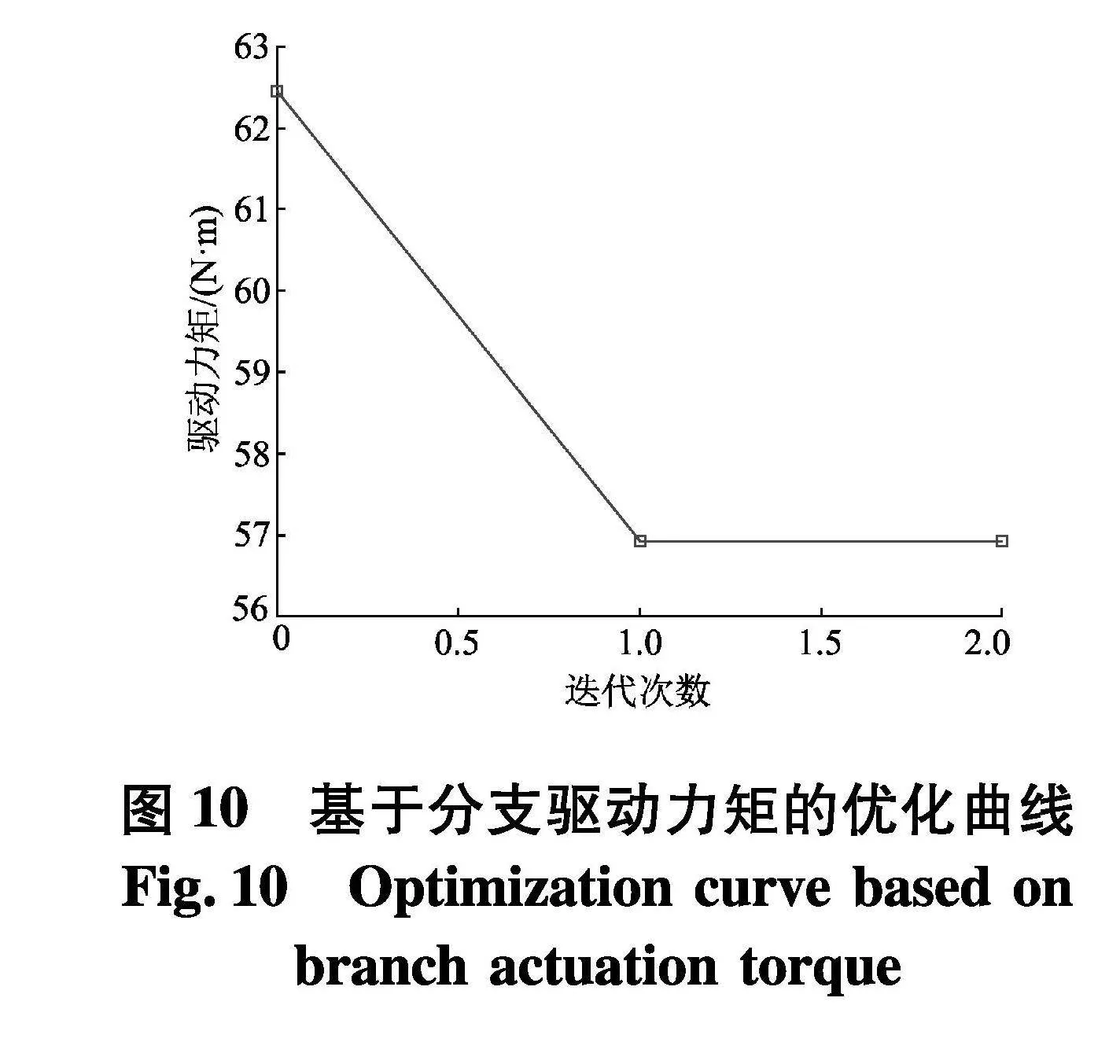
基于参数化分析模块，添加以分支驱动力矩最小的目标函数3组约束条件，优化结果如图10.

基于试验设计和优化分析结果，最终得到一组使机构分支驱动力最小的结构参数，连杆长度L=0.400 m、定平台半径RO=0.130 m、动平台半径RC=0.160 m、动/定平台中心距r=0.530 m.优化后的4组设计变量值与设计研究分析过程的单一变量分析结果以及与试验设计获得的第36组参数值均保持一致.

3.2" 基于分支运动范围的优化分析

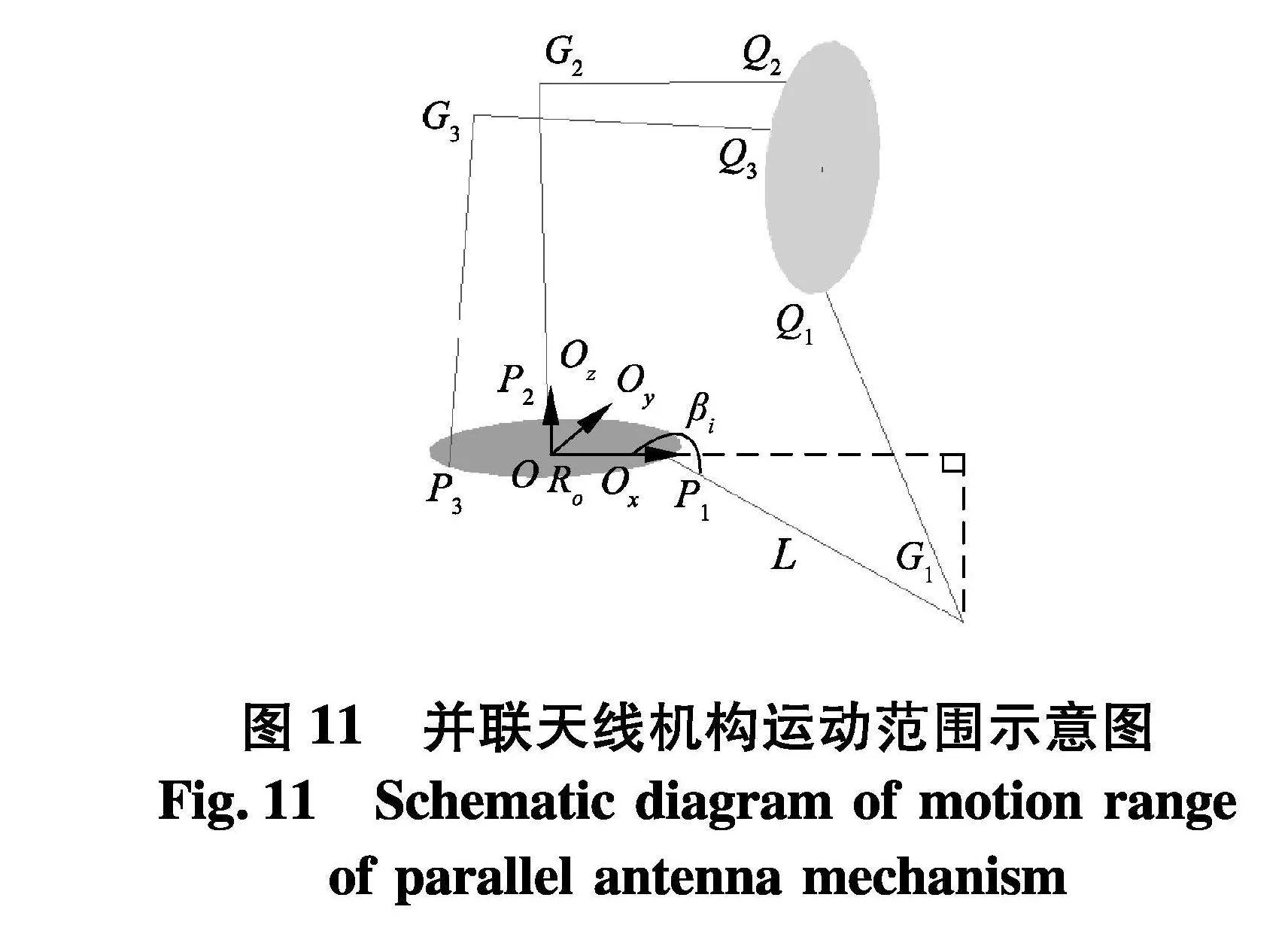
天线安装布置过程中通常需要考虑设备本身的尺寸以及运动过程中的包络空间.当天线反射面大小一定情况下，考虑分支运动范围的优化设计，需要并联天线机构完成特定运动过程中横向运动最大包络空间最小.根据并联天线机构结构特点，铰接点Gi（i=1，2，3）与定平台中心点水平距离可以作为衡量并联天线机构横向最大运动范围指标，如图11.

给定优化设计目标函数，考虑各个分支运动范围最小指标的表达式为：

f（x）=min（max（（RO+Lcosβ1），max（（RO+Lcosβ2），（RO+Lcosβ3））））（13）

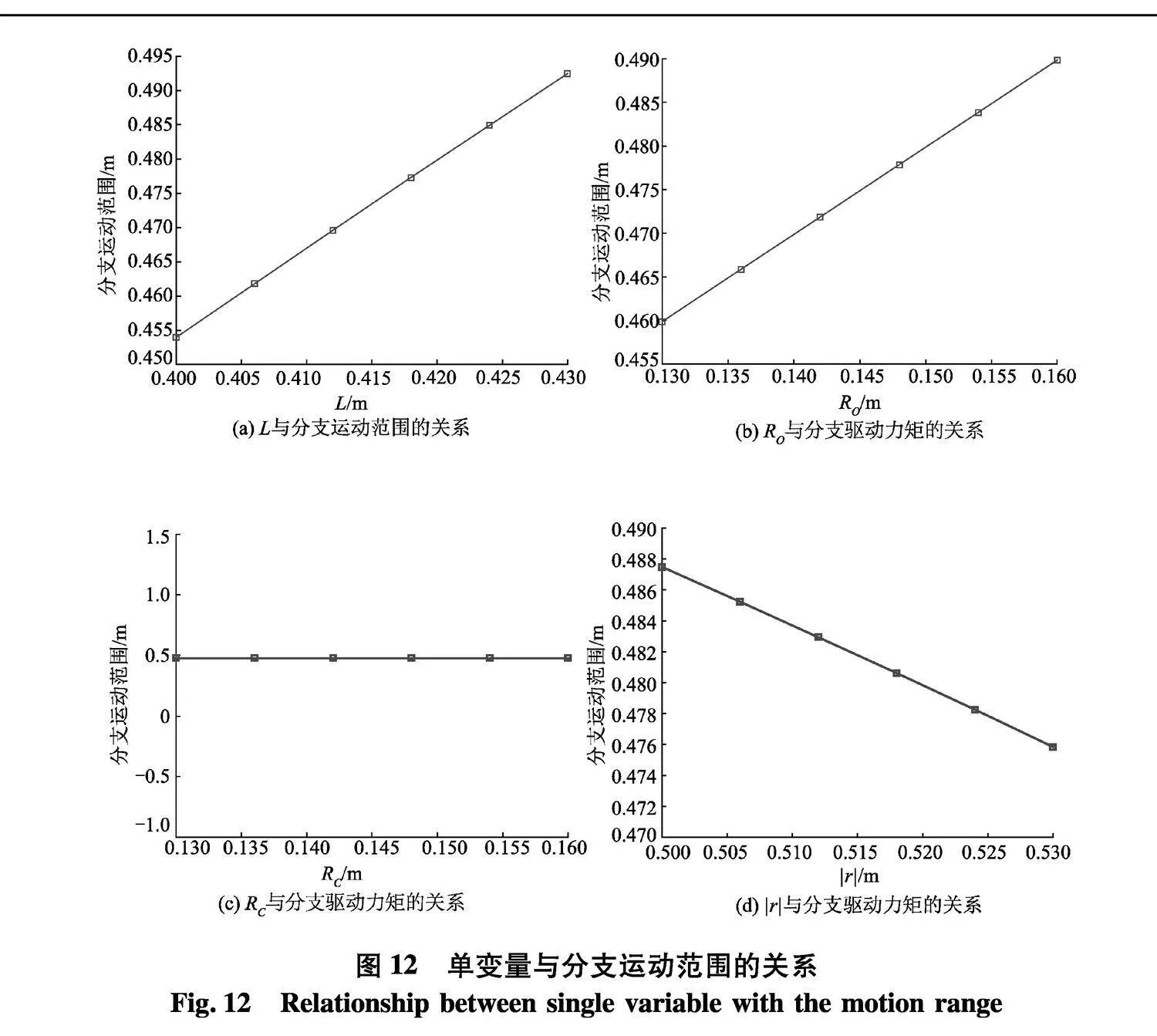
通过参数化分析的设计研究模块，分别研究四组参数对分支运动范围的影响情况，仿真分析结果如图12.

由图12可知，各个分支运动范围极大值随连杆长度L增加而增大；分支运动范围极大值随定平台半径RO增加而增大；分支运动范围极大值随动平台半径RC的增加保持不变；分支运动范围极大值随动/定平台中心距r的增大而减小.

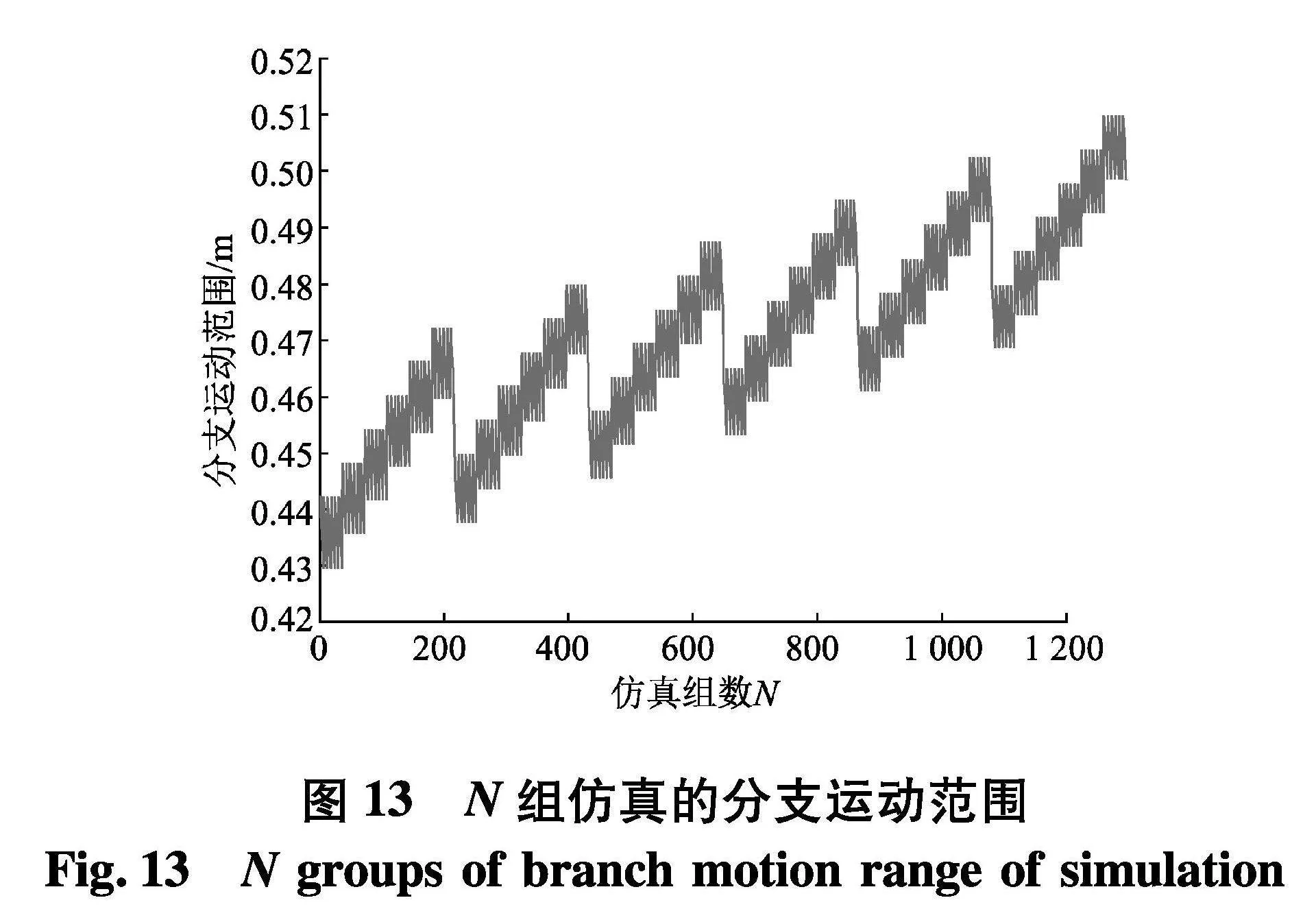
基于参数化分析试验设计功能，给定优化目标和4组设计变量，将设计级别设定为6，即每组设计变量划分为6组数据，共计得到N组构型参数，其中N=64=1 296.基于试验设计模块得到的各组参数与分支运动范围的关系如图13.

如图13，分支运动范围随各组中设计变量变化呈波动上升，取出仿真参数中分支运动范围最大值较小的6组数据，分别为第6、12、18、24、30和36组分支运动范围较小，其参数化变量值如表3.

试验设计得到的6组参数分支运动范围均为0.430 m，通过增加约束条件对数据进行筛选，并联天线机构运动的3组约束条件为：

s.t.0lt;βi≤2π/3" i=1，2，332L（cβ2+cβ3）－RO+15≤033RCsδcζ－rcκ≤0RC2sζsδ+rcκ－36RCsδcζ≤0－36RCsδcζ－RC2sζsδ+rcκ≤0（14）

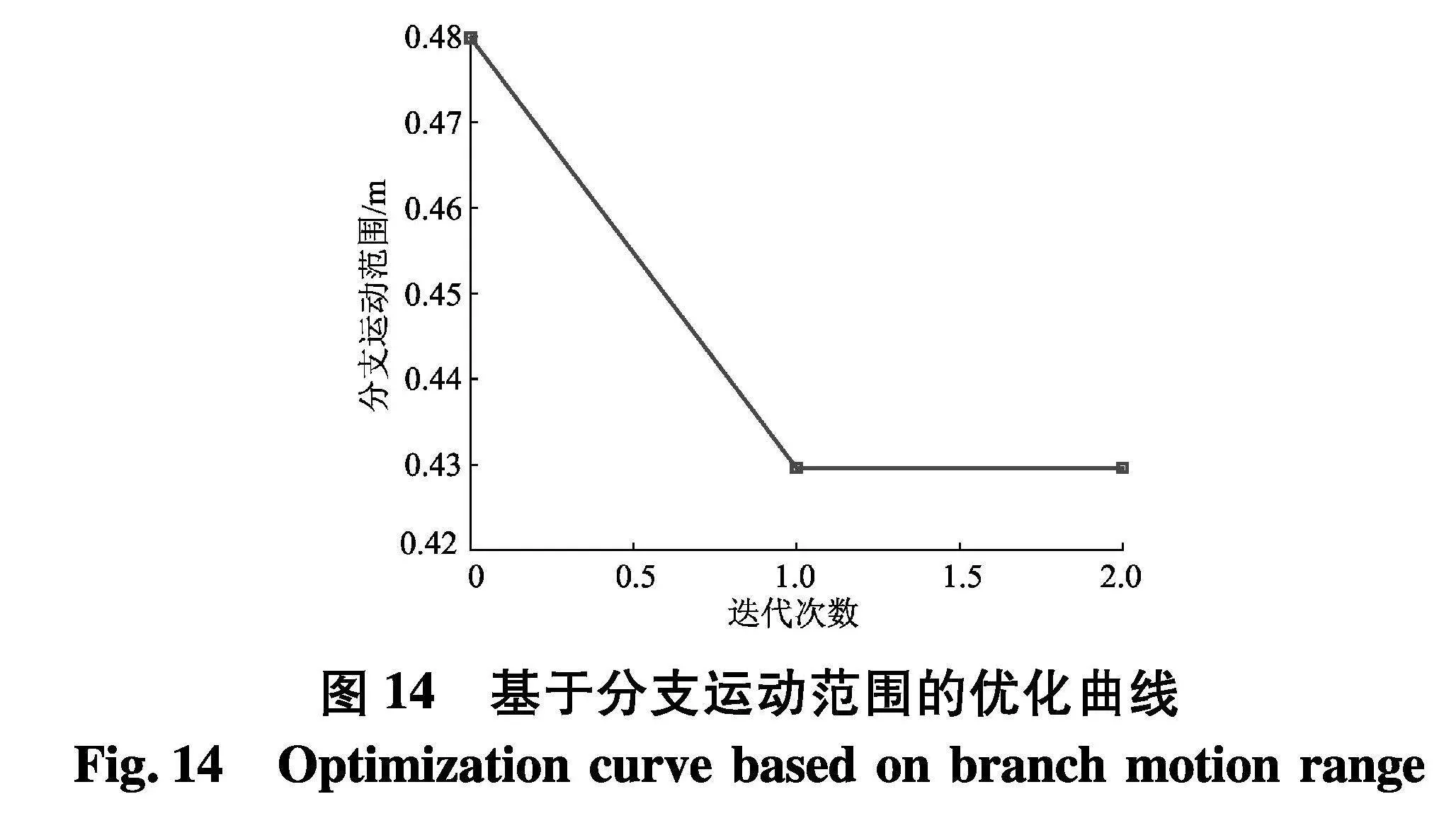
基于参数化分析模块，添加以分支运动范围最小的目标函数3组约束条件，优化结果如图14.

基于试验设计和优化分析结果，得到一组使机构分支运动范围最小的结构尺寸参数，连杆长度L=0.400 m、定平台半径RO=0.130 m、动平台半径RC=0.160 m、动/定平台中心距r=0.530 m.优化分析结果表明，在一定范围内基于分支驱动力矩和分支运动范围设计指标的优化结果相同，最终得到一组使机构性能优异的关键结构尺寸参数.优化结果对天线机构样机研制提供必要的依据.

4" 实验研究

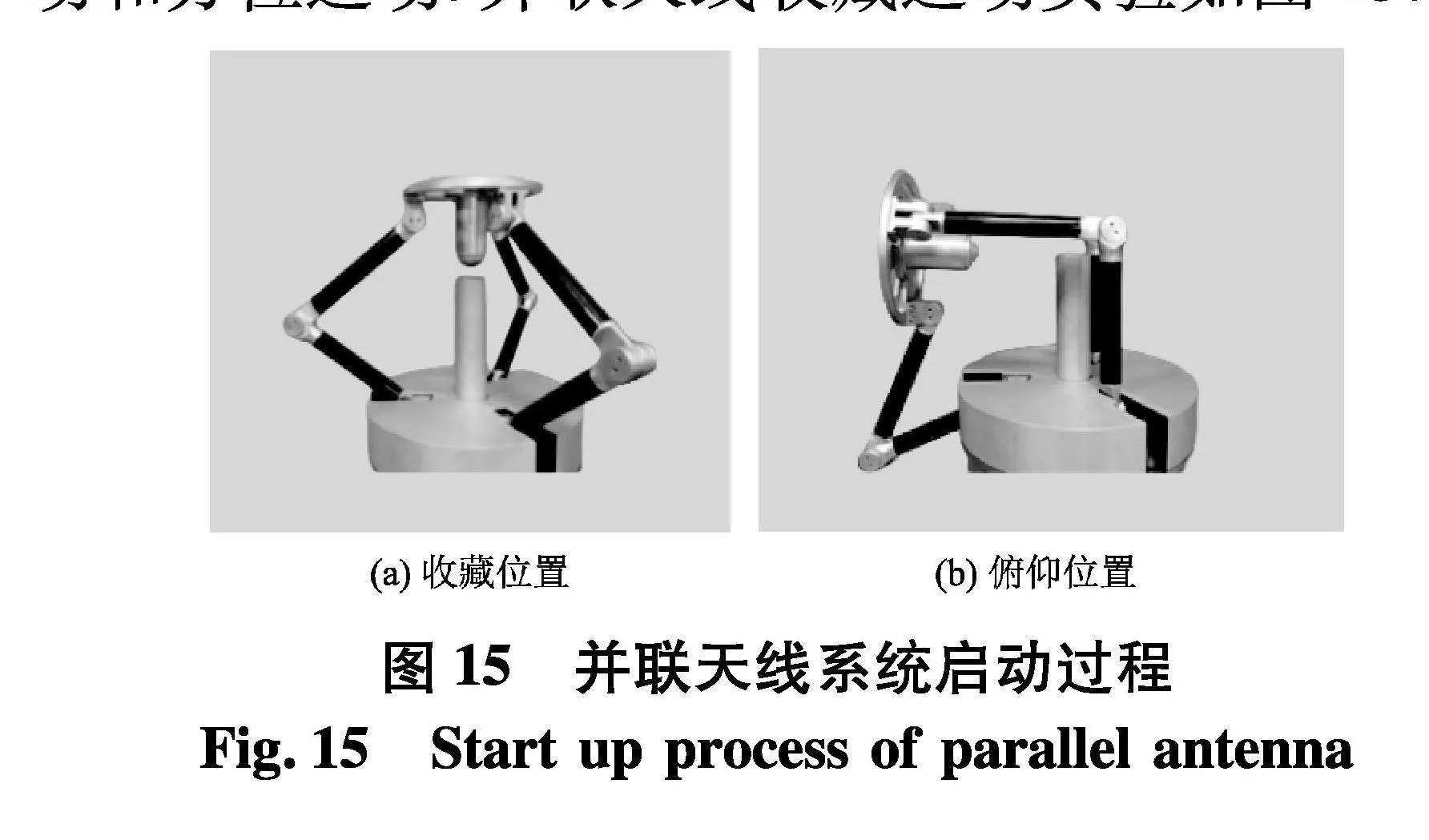
根据优化后的机构结构尺度参数研制实验样机.并联天线主要运动形式包括：收藏运动、俯仰运动和方位运动.并联天线收藏运动实验如图15.

样机实验结果表明，基于优化结构的并联天线能够达到预期运动要求，且运动过程平稳无干涉现象.

5" 结论

（1） 基于并联天线机构结构参数和运动反解模型，在ADAMS参数优化模块建立了并联天线机构参数化模型，根据天线实际运动要求定义机构尺度的设计变量、目标函数及约束条件.

（2） 分别进行了基于分支驱动力矩指标的优化分析与基于分支运动范围的优化分析，得到设计变量与优化目标间的关系，获得满足设计目标要求的机构尺度参数.

（3） 基于机构尺度优化参数，研制了并联天线机构样机，实验样机能够实现方位和俯仰运动，且运动过程中未发生干涉现象.研究工作为天线结构优化设计和样机研制提供参考.

参考文献（References）

［1］" KOCH P M， KESTEVEN M， NISHIOKA H， et al. The AMiBA hexapod telescope mount［J］. Astrophysical Journal， 2009， 694（2）： 1670-1684.

［2］" HUANG Z， LIQ C， DING H F， Theory of parallel mechanisms［M］. Dordrecht ：Springer， 2013：3-14.

［3］" ARTEMENKO Y N， SIL′VESTROV E， KORENOVSKII V， et al. Method for the synthesize of parallel-structure mechanisms for orientating a space telescope antenna［J］. Journal of Machinery Manufacture and Reliability， 2012， 41（4）： 265-269.

［4］" ZHANG G X， ZHENG D H， GUO J W， et al. Dynamicmodeling and mobility analysis of the 3-R（RRR）R+R antenna mechanism［J］. Robotica， 2021， 39（8）： 1-19.

［5］" SONG Y M， QI Y， DONG G， et al. Type synthesis of 2-DoF rotational parallel mechanisms actuating the inter-satellite link antenna［J］. Chinese Journal of Aeronautics， 2016， 29（315）： 330-340.

［6］" 侯雨雷， 赵亚杰， 周治宇， 等. 3-RSR/SP并联车载天线机构运动及力学特性分析［J］. 中国机械工程， 2017， 28（23）： 2799-2808.

［7］" 窦玉超， 侯荣伟， 邓云蛟， 等. 3-RSR构型天线并联机构的结构设计与仿真分析［J］. 机械制造， 2019， 57（8）： 43-47，62.

［8］" 张国兴， 侯雨雷， 曾达幸，等. 四自由度混联天线机构运动特性分析［J］. 中国机械工程， 2020， 31（21）： 2566-2572.

［9］" 许允斗， 仝少帅， 王贝， 等. 2RPU-UPR并联机构在天线支撑中的应用［J］. 中国机械工程， 2019， 30（14）： 1748-1755.

［10］" GUO J W， ZHAO Y S， XU Y D， et al. A novel modular deployable mechanism for the truss antenna： Assembly principle and performance analysis［J］. Aerospace Science and Technology， 2020， 105： 105976.

［11］" 杨彦东， 周治宇， 邓云蛟， 等. 3-RSR型并联车载天线机构动力学优化与仿真［J］. 中国机械工程， 2019， 30（10）：1219-1225，1232.

［12］" SHAO S， SHAO Y， SONG S， et al. Structure and controller design of a piezo-driven orientation stage for space antenna pointing［J］. Mechanical Systems and Signal Processing， 2020， 138： 106525.1-106525.18.

［13］" LI X， DINGX L， CHIRIKJIAN G S. Analysis of a mechanism with redundant drive for antenna pointing［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2017， 231（2）： 229-239.

［14］" 闫文楠， 梁顺攀， 王贝， 等. 一种新型三自由度混联转台的尺度优化分析［J］. 机械设计与制造， 2019（11）： 138-141.

［15］" WANG Y， LIANG J， ZHOU X， et al. Dynamic analysis and structure parameters optimization of a parallel platform based on ADAMS［J］. Applied Mechanics and Materials， 2013， 289： 69-74.

（责任编辑：曹莉）