概率统计重点题型与解题技巧

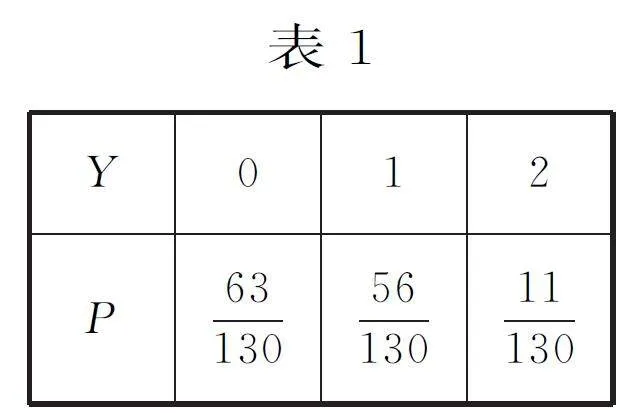
概率统计部分内容多，在现实生活中应用广泛，是高中数学中的重要模块。下面就该模块的重点题型与解题技巧进行梳理，以期对同学们的学习有所启发。

（3）从流水线上任取5件产品，恰有2件产品的质量超过505 g的概率为C2 50.32（1-0.3）3=0.308 7。

点评：抓住问题本质，认准数学模型是解题的关键。本题第二问为超几何分布，第三问为二项分布，超几何分布的本质是把样本分为两类有限抽样，二项分布的本质是独立重复试验。

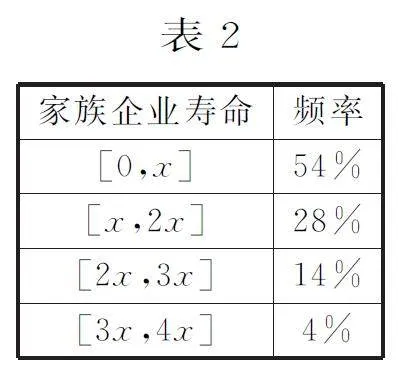
例8 “一世”又叫“一代”。东汉王充《论衡·宣汉篇》：“且孔子所谓一世，三十年也。”清代段玉裁《说文解字注》：“三十年为一世，按父子相继曰世。”而当代中国学者测算“一代”平均为25年。另一家国家研究机构的研究报告显示，全球家族企业的平均寿命其实只有26年，约占总量28%的家族企业只能传到第二代，约占总量14%的家族企业只能传到第三代，约占总量4%的家族企业可以传到第四代甚至更久远（为了研究方便，超过第四代的可忽略不计）。根据该研究机构的研究报告，可以估计该机构所认为的“一代”大约为（ ）。

A.23年 B.22年

C.21年 D.20年

解析：设“一代”为x 年，已知约占总量28%的家族企业只能传到第二代，约占总量14%的家族企业只能传到第三代，约占总量4%的家族企业可以传到第四代，可列出频率分布表，根据平均寿命其实只有26年，利用平均数的求法求解。

已设“一代”为x 年，企业寿命的频率分布如表2所示。

因为全球家族企业的平均寿命其实只有26年，所以家族企业的平均寿命为：

0.54×0.5x+0.28×1.5x +0.14×2.5x+0.04×3.5x=26。

解得x≈22，选B。

点评：同学们要重视应用，学会建模。本题主要考查频率分布表的应用以及平均数的求法，需要同学们具备一定的数学建模能力，才能把实际问题与数学知识联系起来。

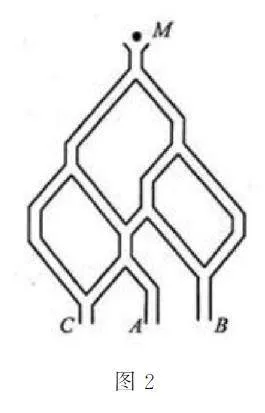
例9 如图2，一个小球从M 处投入，通过管道自上而下落到A 或B 或C。已知小球从每个岔口落入左右两个管道的可能性是相等的。某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则对应获得一，二，三等奖。

（1）已知获得一，二，三等奖的折扣率分别为50%，70%，90%。记随机变量ξ 为获得k（k=1，2，3）等奖的折扣率，求随机变量ξ 的分布列及期望E（ξ）。

（2）若有3人次（投入1球为1人次）参加促销活动，记随机变量η 为获得一等奖或二等奖的人次，求P（η=2）的值。

解析：构建答题模板：

第一步，确定离散型随机变量的所有可能取值;

第二步，弄清每个取值的意义，求出其对应概率;

第三步，列出随机变量的分布列;第四步，求期望;

第五步，回顾解题过程，查看是否有重复或遗漏的情况，规范书写过程。

如本题可重点查看随机变量的所有可能取值是否正确，根据分布列性质检查概率是否正确。

（1）由题意得ξ 的分布列如表3所示。