混凝土立方体抗压数值模拟研究

文章编号10005269（2024）05007806 DOI：10.15958/j.cnki.gdxbzrb.2024.05.11

摘要：为了探究混凝土在单轴压缩下的力学特性，对混凝土立方体受压破坏过程进行数值模拟研究，引入质量缩放技术和单元失效准则提高了数值模拟的精度，结合试验结果给出了适用于混凝土材料的HJC模型参数。结果表明，质量缩放系数和最大主应变参数的取值会对数值模拟的结果产生显著影响，在使用合理的质量缩放系数以及单元失效参数前提下，HJC模型可以较为准确地模拟出混凝土立方体抗压的破坏过程，得到的破坏形态以及应力应变曲线与试验结果的吻合度较好。计算结果为混凝土材料的数值模拟研究提供了一定的参考依据。

关键词：混凝土；立方体抗压；质量缩放；失效准则 中图分类号：TU528 文献标志码：A

混凝土是世界上使用最广泛的建筑材料之一，对其力学性能进行充分研究是混凝土结构设计的前提和基础，但由于部分力学性能试验会受到环境、材料、场地、实验器材等原因的制约，具有一定的局限性。利用计算机软件进行数值模拟研究并根据实验理论可以很好地解决实验中无法解决的问题，因此数值模拟逐渐成为研究混凝土力学性能的常用方法。PENG等［1］利用ABAQUS软件对混凝土进行材料开发，实现了混凝土开裂特性的模拟，能有效地描述冻融混凝土的应力应变演化行为；雷真等［2］基于COMSOL软件模拟了涂层对氯离子侵蚀混凝土的影响，为后续研究提供了参考；郭瑞奇等［3］基于ANSYS/LSDYNA对混凝土材料的动态拉伸力学性能进行了研究，为混凝土类非均质材料的细观数值模拟研究提供了参考；DORCIAK等［4］使用ADINA软件研究了内部结构的尺寸和形状对3D打印结构机械性能的影响，对汽车的生产和航空航天工业的研究打下了坚实的理论基础。

使用数值模拟方法对混凝土在复杂应力下的力学性能进行研究时，选用合理的本构模型、材料参数和失效参数对计算结果的有效性至关重要。其中，HUANG等［5］模拟了岩石的准静态压缩、三轴压缩等实验，提出了岩石材料在高压和高应变率下的计算本构模型；郭瑞奇［6］对一种集束式SHPB装置进行了数值模拟研究，并基于混凝土细观骨料模型的SHPB模拟结果与实验数据进行了对比分析，为实验装置的研制提供了技术支持。王嵩等［7］基于岩石损伤力学对灰岩的单轴抗压试验进行了数值模拟研究，表明修正后的力学参数能够更好地反映岩石材料的破坏过程。

本文基于ANSYS/LSDYNA软件建立了混凝土立方体抗压试验的有限元模型，选取了合理的质量缩放系数以及单元失效参数，对HJC模型参数进行修正，用试验得到的破坏形态及应力应变曲线验证了模型的有效性，为后续研究复杂应力下的混凝土力学性能提供了参考依据。

1计算方法及有限元模型

1.1质量缩放原理

在使用ANSYS/LSDYNA软件进行准静态试验的模拟过程中，常常会遇到计算时间过长的问题。因此，需要使用质量缩放技术［8］来解决这一困扰。运用该技术，可以有效地减少计算时间和存储空间，同时保持模拟结果的准确性和可靠性。此外，在准静态过程中使用质量缩放比动态过程效果更好；当模型包含多个组件时，可只对某些次要部件进行质量缩放，以减弱质量缩放对仿真结果的影响。

质量缩放技术是一种用于提高数值模拟计算效率和稳定性的技术，质量缩放的作用原理是通过在结构某些位置添加非物质质量来提升显式分析的时间步长［9］。在应用质量缩放技术时，相关参数应当设置在一个合理的范围内，否则会影响数值模拟的精度。在动态分析中，任何时候添加质量缩放对仿真结果都具有影响，可从动力学方程MU··+CU·+KU=P（t）看出。公式前面两项为质量惯性和阻尼项，对于动力学过程，当增加不合理的质量时，可能会对结果造成较大的影响，但是对于准静态分析，由于加速度和速度可忽略不计，因此质量增加对结果影响比动态过程小。

分析时间步长受单元尺寸和材料声速的影响：

时间步长：Δt=αL/c（1）

计算总时间：t∝1/Δt（2）

式中：α为比例系数（缺省值取0.9）；L为单元特征长度；c为波在单元的传播速度。

以壳单元为例，声速c与弹性模量E、泊松比v、密度ρ的关系为

c=Eρ（1-v2）（3）

计算总时间：t∝1/Δt∝ρ（4）

由上述公式可知：计算时长与材料密度成正比例的关系，可以通过增大材料密度来提高时间步长，从而减少计算总时间，而增大密度就是质量缩放的手动方法。

质量缩放可通过手动增加物体的密度或者通过设置关键词*CONTROL_TIMESTPE来自动实现，这两种方法是独立的，互不影响。前者是针对整个模型，而后者可对部分结构或单元实现质量缩放，因此推荐后者［10］。质量缩放对进一步提升计算效率有显著效果，它是通过调整质量缩放系数（DT2MS）来执行的。如果DT2MS太小，将达不到缩短计算时间的效果；如果取值太大，会因为质量的增加而造成虚惯性力提高，影响模拟的真实结果，甚至造成计算不收敛。

质量缩放系数（DT2MS）的默认值为0，表示没有进行质量缩放。当DT2MS>0时，所有单元都采用相同的时间步长，并且所有单元均应用质量缩放。当DT2MS<0时，质量缩放只在时间步长小于DT2MS的单元上应用［11］。通常选择DT2MS<0，虽然这可能会轻微增加模型质量并改变质心位置，但可以节省大量计算时间。

1.2单元失效准则

单元失效删除功能［12］是为了弥补有限元方法本身对连续介质的理想化假设而提出的，由于有限元方法的理论基础是连续介质力学，材料单元本身在连续性的理论假设基础上是不可能消失的。但在实际情况下，由于材料的损伤或断裂，一定会导致部分单元消失或完全失效，为了模拟这些现象，ANSYS/LSDYNA提供了单元失效删除功能。

单元失效功能可以在不考虑接触力或约束条件的情况下，预测单元失效后系统的响应［1314］。该技术可以确定失效单元的最小刚度位置以及可能的响应结果，如果一个单元失效，可以将其视为不在计算域内起作用；当大量单元失效时，整个构件就会失效。单元失效准则常用于描述材料的失效过程和形式，从而预测材料的破坏模式和破坏形态，除此还可以预测结构的强度和可靠性，对于准确评估材料和结构的性能和行为非常重要。

HJC模型自带的失效功能通过相关参数Fs来控制，LSDYNA关键字手册［15］中HJC材料模型关键字文件里提到“Fs>0时，当单元的有效塑性应变>Fs失效”，可以将Fs看做是一个应变临界值，当单元的有效塑性应变大于这个值就会失效删除。由于HJC模型中没有控制拉伸失效或者剪切失效的相关参数［16］，无法在数值模拟中精确地控制裂纹扩展现象，需引入关键字MAT_ADD_EROSION来控制单元失效。

关键字MAT_ADD_EROSION有关的侵蚀失效准则包含了多种失效参数，这些参数可以单独使用，也可以几种参数交叉使用。而对于使用哪种失效准则最为准确并没有明确的定论，MA［17］、XIAO［18］等学者研究混凝土的力学性能时使用最大主应变准则和剪切应变准则中的一种或者两种失效准则。考虑到影响材料侵蚀失效的各种因素之间存在着复杂的非线性关系，而立方体抗压试验主要研究压缩变形，因此本文仅研究最大失效主应变εmax对混凝土失效能力的影响，即ε>εmax时单元失效，继而通过修改失效参数MXEPS的值来控制单元失效。

1.3有限元模型的建立

将制作好的混凝土试样在湘潭大学的WAW1000液压万能试验机进行试验，混凝土立方体抗压试验的实体图如图1（a）所示，主要由上压板、下压板和混凝土试样三个部分组成，其中上下压板是直径240 mm、高50 mm的圆柱体，立方体混凝土试样的尺寸为100 mm×100 mm×100 mm；万能试验机的加载方式使用位移加载，控制上压板压缩的加载速率为1.2 mm/min。由于单元尺寸会影响计算步长，单元尺寸越小计算时长就会越长，但是计算精度就会越高，所以应该在保证精度的同时选取合适的单元尺寸。有限元模型按照立方体抗压试验的实体尺寸所建立，模型中的上、下压板和混凝土均采用LSDYNA实体单元库中的三维Solid164实体单元；混凝土和压板均采用六面体单元划分网格，网格尺寸为2 mm，单元总数为1 507 400，节点总数为1 580 383。上压板、下压板、试样分别定义3个Part，压板与试样之间均采用面面自动接触（CONTACT_AUTOMATIAC_SURFACE_TO_ SURFACE），建立的有限元模型如图1（b）所示。

2参数的确定及验证

2.1质量缩放系数的选取

在使用质量缩放技术时，质量缩放系数（DT2MS）应当设置在一个合理的范围内，否则会影响数值模拟的精度。相关文献［810］提到了在准静态实验模拟中遇到计算时长过长的问题时可以使用质量缩放技术，可具体取值范围并没有相关文献提供，因此，本文对DT2MS的合理取值范围进行了探究。此外，计算机的配置会在一定程度影响模拟的计算时间，本次数值模拟采用的工作站配置为：CPU：Intel（R）Xeon（R）Gold5218R CPU @2.10GHz 2.10GHz；内存：128 GB；硬盘：1 TB；本次数值模拟中DT2MS对计算时长的研究基于此工作站结果。如表1、表2所示为不同数量级的DT2MS取值及对应的预估计算时长。可以看出：DT2MS每增大一个数量级，就会使数值模拟计算时长减少至10%左右。当DT2MS取负数时，其取值过大会导致计算终止，无法解决计算时间过长的问题；当DT2MS取正数时，取合理的数值可以有效解决计算时长问题。因此，当DT2MS取一定范围时，可以使计算时长达到一个合适的范围，从而解决立方体抗压数值模拟的计算时长问题。本文DT2MS的合理取值范围为0.001～1。

2.2单元失效参数的选取

在研究混凝土的静、动态力学性能中，单元失效准则的确定和验证是模拟过程中重要的环节，需要结合试验和理论分析进行验证和优化。HJC模型中有自带的失效参数Fs，可以通过调整参数Fs的大小控制单元的失效删除。仅依靠HJC模型中的失效参数Fs对试样破坏形态的影响如图2所示。可以看出：参数Fs=0时，试样发生变形但失效单元并未删除，没有产生裂缝；参数Fs>0时，试样已经产生明显裂缝，可有失效单元未完全删除而又产生畸变的现象；参数Fs<0时，删除的单元较多，以至于产生过多的空洞。结果表明，仅依靠HJC模型失效参数Fs无法有效控制失效单元的删除，与试验的试样破坏形态不符。

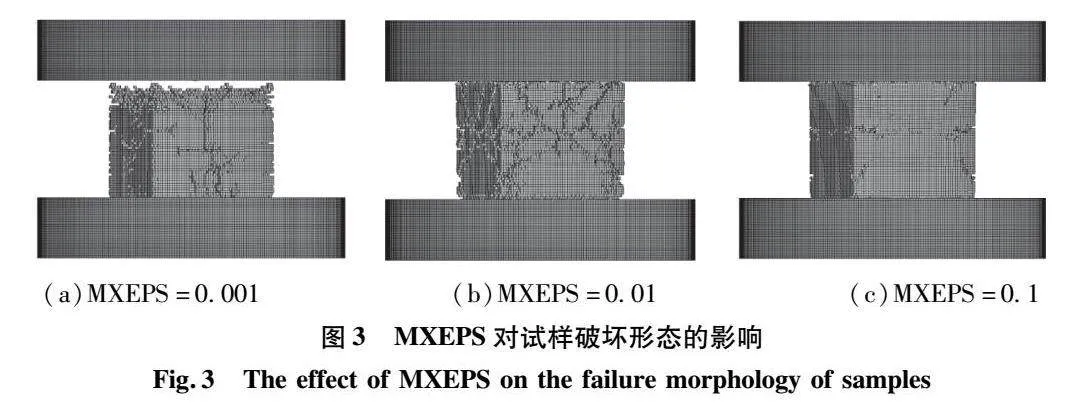
因此，需要引入关键字MAT_ADD_EROSION侵蚀失效准则来控制失效单元的删除，在此仅使用最大主应变失效准则，控制最大主应变失效准则的参数为MXEPS。如图3所示为不同取值的失效参数MXEPS及对应的试样破坏形态。可以看出：MXEPS取值太小会使失效单元删除过多，甚至形成大量空白；而MXEPS取值太大则会导致试样没有发生明显的破坏，甚至会导致单元失效并没有删除而又产生畸变。因此，在本模型中MXEPS最合理的取值范围为0.01～0.1。

2.3材料参数的确定及验证

液压万能试验机的压板只发生弹性变形，可视为线弹性材料，所以数值模拟计算中两个压板均采用线弹性模型，其中：密度ρ=7 800 kg/m3，弹性模量E=200 GPa，泊松比v=0.3。混凝土试样采用HJC本构模型，该模型是针对混凝土材料提出的计算模型，它综合考虑了应变率效应、损伤演化效应、围压效应和压碎、压实效应的影响。

经过一系列的静态力学试验，获得材料基本参数如密度ρ、抗压强度fc、剪切模量G以及抗拉强度T，假设压缩的损伤因子与材料的强度无关，参考JOHNSON等［19］在提出HJC计算模型时，给出了静态抗压强度为48 MPa的混凝土原始HJC模型参数取值，损伤参数D1、D2、εf，min取原始值，Pcrush=fc/3，参数Plock、μlock、K1、K2、K3、Smax、0和Fs参考原始取值，参数A、B、N、C、μcrush根据原始取值进行调试，得到混凝土立方体抗压HJC模型材料参数如表3所示。

经过多次数值计算，得到质量缩放系数DT2MS取0.2，最大主应变失效参数MXEPS取0.015为本模型的最佳取值。在此基础上，对修正后的混凝土HJC模型材料参数进行数值模拟。由图4可以看出模拟的试样表面形成一条X形状的

裂缝，最后呈现出上下近似对称的一对圆锥体破坏形态，与试验结果有较高的吻合度，验证了参数的有效性。如图5所示为不同时间下混凝土模型的损伤应力云图。在加载初始阶段，混凝土处于弹性破坏，应力集中在试样上端部，由于数值模拟中使用失效准则的原因，试样上端面会有部分单元先失效删除；随着加载的进行，轴向变形逐步增大，下端部应力开始集中并出现裂缝，随后试样表面的裂缝逐渐延伸贯通，应力集中在裂缝贯通的位置；最终，试样逐渐失去承载能力，达到图示应力平衡的状态。

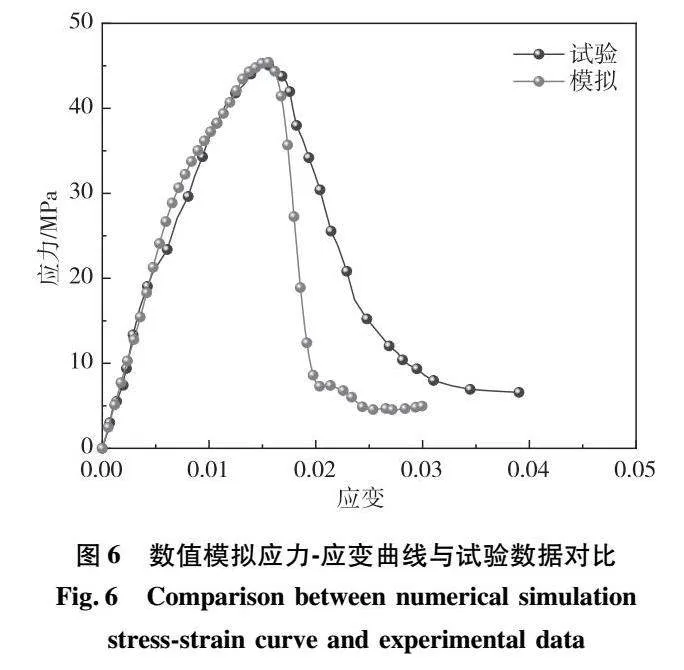
数值模拟的应力应变曲线与试验曲线经过对比，如图6所示，可以看出模拟数据和试验数据在加载阶段的应力应变曲线与试验曲线有较高程度的吻合，而卸载阶段却有一定的误差。因为在试验的卸载段，试样裂缝处的结构存在压实过程，裂缝周围的间隙会被周围的材料填充，会有一定的缓冲效果；而数值模拟中，由于使用侵蚀失效删除准则，单元失效后会被立即删除，单元删除后的间隙不会有材料填充，所以在卸载阶段数值模拟的曲线较陡；误差在可接受的范围内，验证了数值模拟模型的可靠性。

3结论

利用ANSYS/LSDYNA有限元软件，对混凝土立方体抗压试验进行了数值模拟研究。针对本文的模型得到以下结论：

1）采用质量缩放技术可以有效解决准静态模拟中计算时间过长的问题，DT2MS的合理取值范围在0.001～1，本文最佳取值为0.2。

2）单元失效参数MXEPS的合理取值范围在0.01～0.1内可以有效模拟出混凝土立方体抗压试验的破坏损伤，本文最佳取值为0.015。

3）通过调试HJC模型的部分参数，可以有效模拟混凝土立方体抗压试验的破坏过程，利用试验的破坏形态以及应力应变曲线验证了HJC模型在混凝土立方体抗压试验模拟的适用性。

在后续的研究中，可以在本文数值模拟结果的基础上进行关键参数的敏感性分析，为后续基于三维细观模型对混凝土材料进行单轴应力作用下的力学性能及破坏机理的数值模拟研究提供一定的参考依据。

参考文献：

[1]PENG R X， QIU W L， TENG F. Threedimensional mesonumerical simulation of heterogeneous concrete under freezethaw［J］. Construction and Building Materials， 2020， 250： 118573.1118573.10.

［2］ 雷真， 陈敬男， 杨洋，等. 涂层混凝土氯离子扩散的修正模型与数值模拟［J］. 混凝土， 2023（1）：3540.

［3］ 郭瑞奇，任辉启，龙志林，等.大直径SHTB实验装置数值模拟及混凝土细观骨料模型动态直拉研究［J］.爆炸与冲击， 2020， 40（9）： 1831.

［4］ DORCIAK F， VASKO M， HANDRIK M， et al. Tensile test for specimen with different size and shape of inner structures created by 3D printing［J］. Transportation Research Procedia， 2019， 40： 671677.

［5］ HUANG X P， KONG X Z，CHEN Z Y， et al. A computational constitutive model for rock in hydrocode［J］. International Journal of Impact Engineering，2020，145： 103687.1103687.12.

［6］ 郭瑞奇. 大直径Hopkinson杆混凝土材料动态压缩和拉伸特性研究［D］. 湘潭：湘潭大学， 2022.

［7］ 王嵩，左双英，曲传奇，等.基于单轴压缩试验的岩石损伤力学参数修正及数值模拟［J］.贵州大学学报（自然科学版），2017，34（2）：109114.

［8］ NEUVONEN R， SKRIKO T， BJORK T. Use of the quasistatic JohnsonCook model in the failure assessment of tensile specimens with metallurgical constraints［J］. European Journal of MechanicsA/Solids，2020，82： 104011.1104011.15.

［9］ ABDELWAHED B. Nonlinear numerical simulation for reinforced concrete elements with explicit time integration procedure［J］. Case Studies in Construction Materials， 2020， 12： e00344.1e00344.9.

［10］COCCHETTI G， PAGANI M， PEREGO U. Selective mass scaling and critical timestep estimate for explicit dynamics analyses with solidshell elements［J］. Computers & Structures， 2013， 127： 3952.

［11］熊刚. 基于LSDYNA的车辆与半刚性护栏碰撞的有限元仿真［D］. 武汉：华中科技大学， 2021.

［12］林琛， 徐建军， 杨晋伟， 等. 基于HJC模型的钢筋混凝土侵彻仿真失效准则与参数［J］. 探测与控制学报， 2017（2）：100105.

［13］孙其然， 李芮宇， 赵亚运， 等. HJC模型模拟钢筋混凝土侵彻实验的参数研究［J］. 工程力学， 2016（8）： 248256.

［14］汪衡，汪于程， 蔡金良，等.HJC模型失效参数对侵彻能力影响的数值研究［J］.兵器装备工程学报，2020，41（10）：150155.

［15］LSTC. LSDYNA keyword user’s manual［M］. California：LSTC， 2013.

［16］马爱娥，黄风雷，初哲，等.弹体攻角侵彻混凝土数值模拟［J］.爆炸与冲击，2008（1）：3337.

YWLL5+NycGQvwwr1ke+PB5pYd8tBcZXuJGFQOKJmI28=

［17］MA H Y， WU Z Y， ZHANG J H， et al. Uniaxial compressive properties of ecological concrete： experimental and threedimensional （3D）mesoscopic investigation［J］. Construction and Building Materials， 2021， 278： 121034.1121034.13.

［18］XIAO Y， ZHU W Q， WU W C， et al. Damage modes and mechanism of RC arch slab under contact explosion at different locations［J］. International Journal of Impact Engineering， 2022， 170： 104360.1104360.17.

［19］HOLMQUIST T J， JOHNSON G R， COOK W H. A computational constitutive model for concrete subjective to large strain， high strain rates， and high pressure ［C］// JACKSON N， DICKERS S.The 4th International Symposium on Ballistic. Quebec： American Defense Prepareness Association， 1993： 591600.

（责任编辑：曾晶）

Abstract：

In order to explore the mechanical properties of concrete under uniaxial compression， the compressive failure process of concrete cube was numerically simulated， the mass scaling technique and element failure criterion were introduced to improve the accuracy of the numerical simulation， and the concrete HJC model parameters were debugged. The results show that the values of the mass scaling coefficient and the maximum principal strain parameter will have a significant impact on the numerical simulation results， and under the premise of using reasonable mass scaling coefficient and unit failure parameters， the HJC model can accurately simulate the failure process of concrete cube compression， and the failure morphology and stressstrain curve are in good agreement with the test results.The research results provide a certain reference for the numerical simulation of concrete materials under complex stress conditions.

Key words：

concrete; cube compression resistance; mass scaling; failure criterion

收稿日期：20231116

基金项目：湖南省自然科学基金资助项目（2023JJ40610，2023JJ30569）；湖南省教育厅优秀青年项目（23B0124）；湖南省研究生科研创新项目（QL20230162）

作者简介：董杰（2000—），男，在读硕士，研究方向：混凝土材料工程数值模拟，Email：qswh_dj@163.com.

*通讯作者：郭瑞奇，Email：grq@xtu.edu.cn.