极限平衡法与强度折减法在边坡稳定分析中的问题讨论

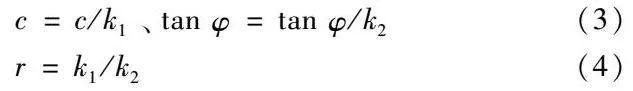





文章编号1000-5269(2024)05-0070-08 DOI:10.15958/j.cnki.gdxbzrb.2024.05.10
摘要:为比较极限平衡法与强度折减法在边坡稳定分析中的区别,通过具体算例,将瑞典条分法、简化Bishop法、Janbu法等不同的极限平衡方法和有限元软件中强度折减法(SRM)应用于工程实践中,通过多种计算方法求解边坡安全系数,并对两种均质土坡稳定性结果进行分析。结果显示瑞典条分法可信度较低,安全系数仅为089。采用正交试验探讨了网格疏密对安全系数的影响,Abaqus所得等值线最深。此外,通过比较不同方法所得安全系数和临界滑动面,进一步探讨边坡失稳和滑动面搜索等问题。研究结果可对极限平衡法与强度折减法在工程中的应用提供一定的参考。
关键词:强度折减法;边坡稳定分析;滑动面搜索;数值模拟;正交试验 中图分类号:TU411 文献标志码:A
边坡稳定性分析是岩土工程的热点问题,涉及矿山工程、水利水电工程等诸多工程领域[1]。目前,常用的边坡稳定性分析方法主要有极限平衡法和强度折减法两种。极限平衡法是一种经典的边坡稳定分析方法,具有计算简单、直观明了、工程实践经验丰富等优点,但也存在一些缺点,如不同的条分法计算结果之间有偏差[2]。强度折减法在1975年ZIENKIEWICZ[3]率先用于边坡稳定有限元分析中,随着科技的发展,国内很多学者利用强度折减法作出了许多成果。程灿宇等[4]利用MIDAS/GTS、FLAC和ANSYS三种软件采用强度折减法配合(D-P)屈服准则和(M-C)屈服准则分别对不同工况的边坡进行分析。杨才等[5]则以经典边坡算例分析,采用Abaqus有限元软件用强度折减法计算,归纳出边坡失稳时的等效塑性应变达到的数量级。王思源等[6]则采用动态强度折减法来搜索边坡滑动面,并提出了改进的矢量和法,以更好地求解边坡稳定性问题。然而,该方法仍然存在一些不足之处:赵尚毅等[7]指出其对边坡失稳的依据没有明确的规定;陈国庆[8]指出了对于滑动面位置的确定还存在不足,强度折减法获得的塑性区过大,不符合实际的边坡失稳特征。对于多层非均质边坡而言,滑动面穿过不同土体,采用相同的折减系数可能不够合理,需要进一步探究。滑动面搜索也是解决边坡失稳的关键点。大量学者的研究表明对滑动面的位置探索有较大出入。
本文旨在将这两种方法更好地应用于工程实践中。通过具体算例,采用理正岩土软件基于不同的极限平衡法(瑞典条分法、简化Bishop法、Janbu法)对边坡安全系数进行求解,并针对边坡算例特例特性,采用AbaqusCAE及MidasGTS有限元软件利用强度折减法(SRM)求解。将两种均质土坡稳定性结果进行了分析,并从安全系数与临界滑动面两方面进行了对比,此外利用正交试验探讨了网格疏密对安全系数的影响以及对边坡失稳和滑动面探索的讨论。
1边坡稳定性分析原理
1.1极限平衡法
极限平衡法作为一种经典边坡稳定分析法[9],将边坡失稳过程简化为一个滑动土体沿着未滑动土体滑动,通过对滑动面上土体间平衡状态判定边坡稳定性。对一二维平面滑动体,其安全系数可表示为
Fs=cl+NtanφT(1)
式中:Fs为安全系数;c、φ为土体黏聚力、内摩擦角;N为滑动面法向力;T为滑动面切向力;l为滑动面长度。
对于黏性土边坡滑动面一般非平面,若对滑动面进行平衡分析就要求将滑动体离散成n个竖直的土条,每一土条沿底部滑动的安全系数相同,各土条宽度很小可将其底面视为平面,滑动面上的力作用于土条底边中点。在此基础上发展而来的有瑞典条分法、简化Bishop法、Janbu法、Spencer法等众多基于以不同假定实现高次超静定降维求解的极限平衡分析法[9-10]。
瑞典条分法假定滑动面为一圆弧,不考虑土条间力,从而得出安全系数Fs的显性表达式。因其未考虑条间力,计算所得安全系数过于安全,对于不考虑地下水影响的一般工程可进行粗略计算,便于工程人员接受与应用。
简化Bishop法与Janbu法均在瑞典条分法的基础上考虑了土条间法向作用力,不同的是Bishop法采用圆弧滑动面,Janbu法适用于任意形状滑动面。两种方法都考虑了条间力作用,有明确的Fs隐性表达式,可通过迭代求解,对于均质边坡的计算结果足够精确且一般比瑞典条分法所得安全系数大。
1.2强度折减法
随计算机技术的发展,ZIENKIEWICZ[3]于1975年将强度折减法(SRM)应用于边坡稳定有限元分析中。目前,常用有限元及有限差分软件Midas、Abaqus及Flac都增加了这一功能,具体原理如下:
若记c′、φ′为
c′=c/Fs,tanφ′=tanφ/Fs(2)
则可将强度指标按式(2)进行折减,采用折减强度指标c′、φ′对边坡进行弹塑性计算。将折减系数(安全系数)Fs由一个较小的值逐渐增大,边坡处于临界破坏状态时,Fs即为边坡最小安全系数。
对于边坡临界破坏状态的直观判定准则主要有[6,10]:
(1)有限元计算不收敛;
(2)广义或等效塑性区贯通至坡顶;
(3)坡脚或坡顶某一点位移发生突变。
三项判定准则在某些情况下并不完全等同,例如程灿宇等[4]在对不同有限元软件强度折减法应用的分析中,Ansys软件多次出现塑性区不贯通但计算不收敛,迭代停止。基于现有研究及极限平衡法对失稳状态的判定,同时结合实际工程经验,得到有限元计算不收敛不可作为一单独判据这一结论,应将等效塑性区贯通坡顶与某点位移突变相结合作为基准判据,同时视有限元迭代情况对安全系数综合取值。
强度折减法无需假定滑动面形状与位置,有限元软件可直接得出安全系数并可直观显示边坡破坏过程,现已广泛应用于二维、三维边坡稳定性分析与治理中。但对于多层非均质边坡而言,滑动面穿过不同土体,采用相同的折减系数不尽合理,还需进一步探究。
2边坡稳定分析与结果对比
2.1算例
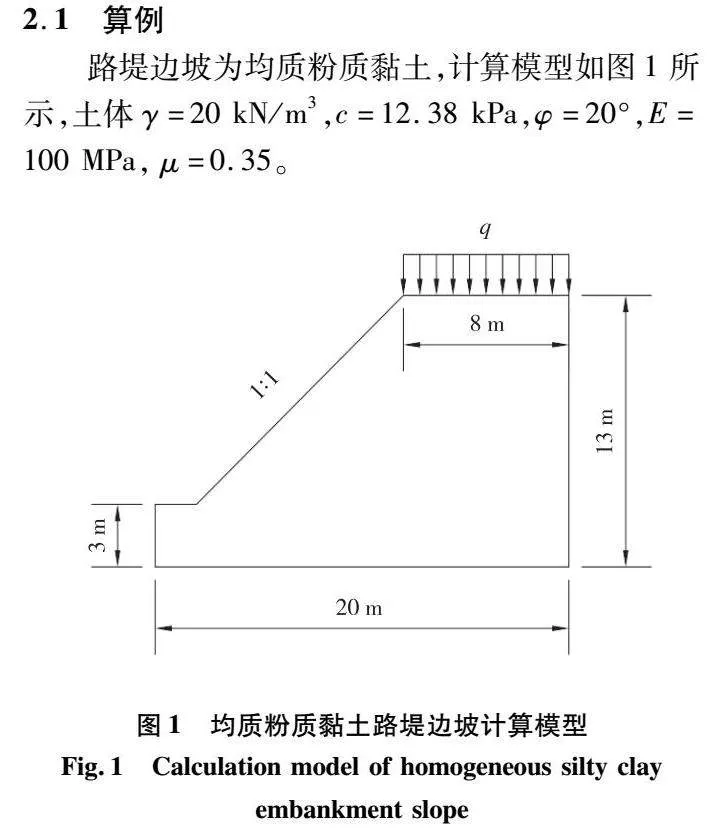
路堤边坡为均质粉质黏土,计算模型如图1所示,土体γ=20kN/m3,c=12.38kPa,φ=20°,E=100MPa,μ=0.35。
2.2极限平衡法求解
现已有较多极限平衡计算法编程软件,工程应用效果良好。为简化分析过程,这里采用理正岩土软件对算例边坡采用瑞典条分法、简化Bishop法、Janbu法安全系数分别求解。值得注意的是,据极限平衡法原理对均质边坡滑动面的假定,若滑动面处于模型边界内,计算精度并不受边界范围影响。
2.3有限元SRM求解
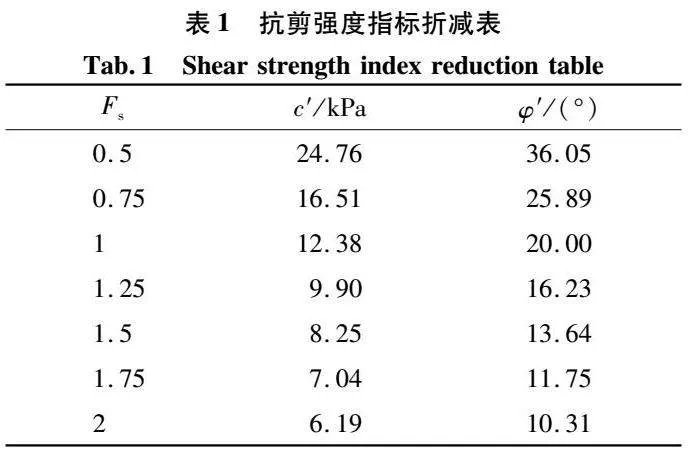
针对该算例边坡稳定性,此次采用AbaqusCAE及MidasGTS有限元软件利用强度折减法(SRM)求解。建模尺寸与算例尺寸一致,土体假设为理想弹-塑性体,采用Mohr-Coulomb屈服准则。边界条件设置为左右边界x向约束,下方边界x-y向限制。强度折减系数Fs设为0.5~2.0,按增幅为0.25依次增加,则由式(2)得抗剪强度指标迭代值如表1。将其以场变形式输入Abaqus材料属性程序,并对Midas中SRM分析步进行设置。有限元二维计算模型运算结果如图2、3所示。
2.4结果分析
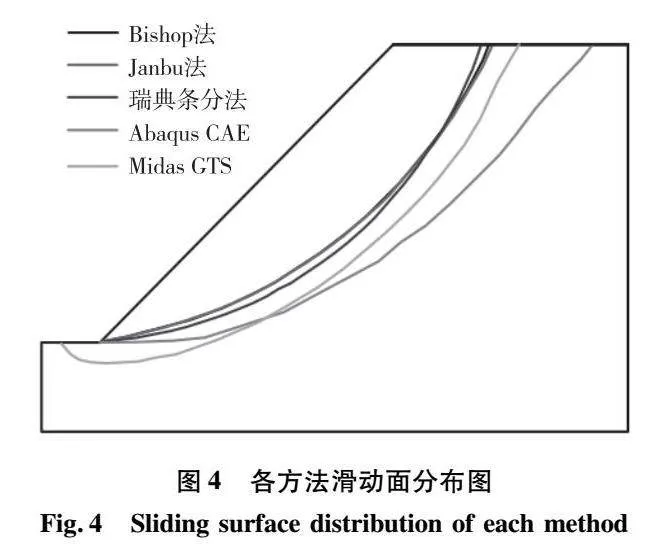
理正极限平衡分析所得滑动面与安全系数可直接输出,据1.2节所述破坏准则整理Abaqus与Midas迭代结果,为减小迭代误差,安全系数保留小数点后两位。基于极限平衡法滑动面后方土体不滑动、无位移的假设,临界滑动面以位移等值线为0进行刻画,分析结果如表2及图4。
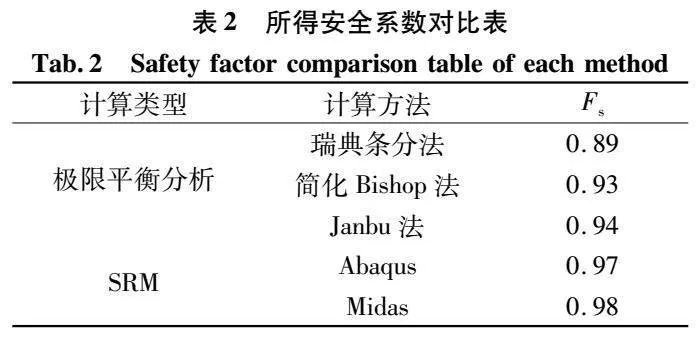
由表2可知,对于该二维均质边坡算例瑞典条分法所得安全系数最低,Midas所得最高,极差约为9%。简化Bishop、Janbu法、Abaqus及Midas所得安全系数依次增大,4种方法极差仅有5%,结果较为吻合。因此,可认为该4种方法具有较高的可信度,算例安全系数处于0.93~0.98之间,均表现为失稳状态。三种极限平衡法所得结果差异符合土体失稳基本模式。其中,瑞典条分法忽略了条间力作用,所得结果偏小。简化Bishop法考虑了土条间法向力,使安全系数在瑞典条分法基础上增大约4%。Janbu法将土条间法向与切向力均考虑在内,又将安全系数提升1%。这说明条间力对边坡稳定有利,条间法向力对稳定性的影响大于条件切向力,符合目前研究[9,11-12]结论所述规律。在计算条件允许的情况下,应当优先选用考虑更加全面的Bishop或Janbu法并对比两者结果,综合取值。
从两种有限元SRM结果来看,强度折减法所得安全系数比极限平衡法大约3%~4%。结合其他学者的对比算例,有限元SRM所得结果均表现出大于极限平衡法。原因可能在于失稳判据的主观性,有限元计算程序的不可视性。目前,有限元SRM仍存在众多争议与不确定性,但其计算精度满足一般工程要求,可与极限平衡法结合运用以提高结果可信度。
据图4所示,该算例三种极限平衡法所得滑动面相差不大,两种有限元SRM所得滑动面相差较大,且均比极限平衡法所得分布深。其中,极限平衡法与Abaqus所得滑动面均穿过坡脚,Midas所得滑动面分布深度介于极限平衡法与Abaqus之间,Abaqus所得滑动面分布深度较其他方法差别较大,滑动面均表现出有限元SRM深于极限平衡法所得。值得注意,所建本算例Abaqus计算模型滑动面分布深度差别太大,极可能具有特殊性。故对边坡加固时,应充分结合工程经验估算滑动面位置以确定加固范围,必要时采用偏保守结果。
有限元强度折减法无需假定滑动面,可直接定义模型状态即可完成各项运算并将应力、变形可视化,可应用于各种复杂边坡稳定性分析与支护设计,与极限平衡法相比具有更广的适用性与操作性。但计算模型的建立过程以及准则的选用都对结果存在相应影响,要求一定的建模经验。
3强度折减法相关问题的讨论
1、2节通过极限平衡法与强度折减法对算例边坡稳定性进行分析并得出对比结论,同时有限元SRM计算模型边界条件、计算范围及网格质量对计算结果存在一定程度的影响。本节对强度折减法计算影响因素、折减方法与广泛争议作如下讨论。
3.1有限元SRM计算影响因素
3.1.1正交试验
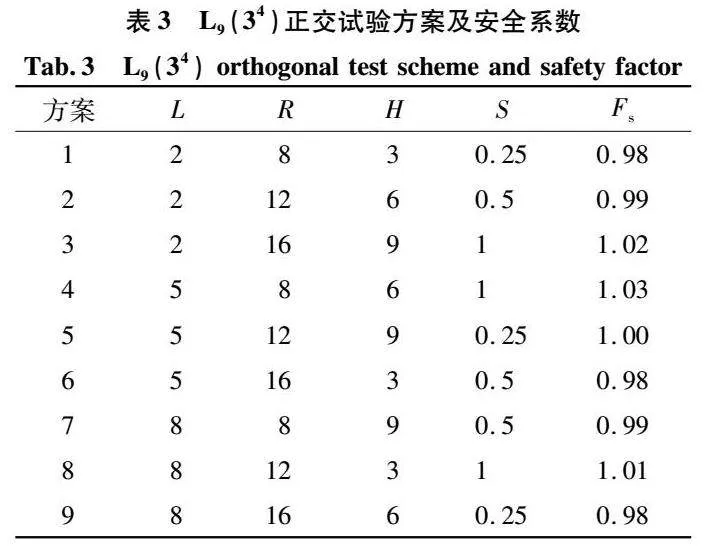
据此次建模经验,有限元SRM计算精度主要受到模型边界、网格质量的影响,除此外迭代系数、收敛因子及屈服准则均会对计算结果有影响。杨有成等[13]对此做了充分研究并得出了共性结论。利用正交试验法[14]设计建模方案,以对模型边界、网格质量的影响进行分析。在算例的基础上,定义边坡左边距L、右边距R、底边距H,边坡坡度与长度保持不变,坡顶超载为20kPa,分布范围8m,以网格尺寸S衡量网格疏密程度。其中,L水平设置为2、5、8m,R水平设置为8、12、16m,H水平为3、6、9m,综合考虑模型运算时间与一般经验将S设置为0.25、0.5、1m。由此构建四因素三水平正交试验方案L9(34),将81组模型缩减为9组,大幅降低建模及运算时间。试验方案L9(34)及安全系数如表3。
3.1.2试验结果分析
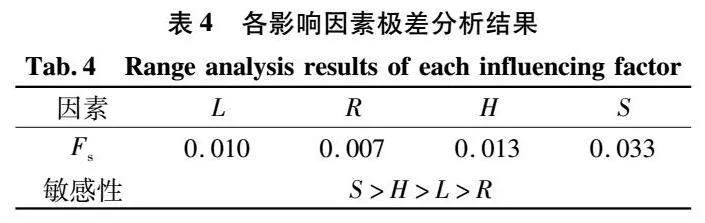
极差分析法通过极差分析与效应趋势图进行综合比较得出试验结论,设每列第i水平计算结果和为yi,则有均值Ai=yi/s,其中,s为每列所含水平数,均值Ai确定同一因素不同水平对指标的影响。极差R=maxAi-minAi,极差决定各因素对指标的影响程度。据表3绘制影响因素极差分析表及效应趋势图如图5所示。
由表4及图5可知网格尺寸S对安全系数的影响敏感度最高,底边距H次之,右边距R最低。其中,S对安全系数的影响达到3%以上,边界尺寸因素的影响均在1%左右,几乎可忽略。本文网格尺寸差仅为0.75m,当差值进一步增大时,其对安全系数的影响将进一步扩大。如杨有成等[13]给出的算例结果显示当网格尺寸差为1.5m时,所得安全系数最大可相差9%。综合正交试验结果与既有研究可知,网格疏密对安全系数的影响较大,网格越密集,所得结果越小,结果越精确。随网格密度进一步增大,安全系数变化幅度逐渐减小并稳定在一真实值附近。同时,网格越密集则有限元结果可视化效果越好。
对于本算例而言,模型边界范围对计算结果影响并不大。但在对其他经典算例的研究中边界范围对结果的影响可达5%。一般建模经验表明,边界范围至少取左边距L为1.5倍坡高、右边距R为2.5倍坡高、底边距H为1倍坡高。但边界范围也不宜过大,以免模型运算时间过长,所得结果与极限平衡法相差太大失去说服性与对比性。
3.2有限元SRM其他问题
3.2.1边坡失稳判据的讨论
目前常用的SRM边坡失稳判据主要有3类:有限元计算不收敛;坡顶等其他特征点位移突变;广义或等效塑性区贯通坡顶。对于这3类判据,许多学者对其有效性与统一性进行了广泛讨论。赵尚毅[15]、吕庆[16]和龙绪健[17]等均认为塑性区贯通是破坏的必要非充分条件,只有当塑性区贯通后,塑性应变产生不可控增长才可说明边坡失稳破坏。刘祚秋[18]、刘金龙[19]等则认为采用塑性区贯通判据作为边坡破坏的标准是合适的。陈力华[20]等认为3类失稳判据具有统一性,边坡发生整体破坏是因塑性区从坡脚到坡顶贯通而产生无限的塑性流动,特征点位移将相应的突然增大,有限元数值计算因位移无限增长而无法收敛,因此,三类失稳判据理论上是统一的。赵尚毅等[7]同样认为塑性区贯通并不代表发生失稳破坏,仅当土体屈服塑性区贯通且产生无限发展的塑性应变与位移,进而有限元计算不收敛,也即塑性区贯通为必要条件,不收敛与位移突变两者相伴而生作为失稳判据。
此次算例建模经验表明塑性区贯通、位移突变及计算不收敛在有限元分析中并不总是同步发生。塑性区贯通往往先于位移突变发生,有限元计算不收敛后于突变发生。这一点与GRIFFITHS[21]等所得经验一致。王栋[22]、程灿宇[4]等发现数值计算不收敛既可能发生在特征点位移突变时,也可能发生在特征点位移突变后,或是计算不收敛在塑性区贯通之前和之后都可能发生。此次建模过程中也少量出现这种情况,但通过调整运行参数最终有限元计算不收敛都出现在塑性区贯通与位移突变后。此外,算例建模过程中发现塑性区贯通、位移突变间迭代差很小,往往折减系数差仅在0.5%,有限元计算不收敛折减系数差稍大1%~2%。
总结而言,塑性区贯通并不一定代表失稳破坏。塑性区贯通仅是破坏的必要条件,当进一步迭代,增大折减系数后发展为无限增长塑性应变与位移,最终有限元计算表现为不收敛。在模型建立正确、参数合理、有限元程序稳定时,三种判据具有统一性。但工程人员建模时往往不能满足全部条件,进而表现出三种判据所得折减系数不同。这里给出如下建议:
(1)有限元计算不收敛必须保证最后出现,当其先于位移突变时应对模型参数进行调整。
(2)当塑性区贯通与位移突变判据所得折减系数差<1%时,采用位移突变判据更加合理并可满足一般工程精度需求。
(3)当计算不收敛折减系数差<4%且由(2)所得安全系数与极限平衡法结果相近时,可不必过于追求判据出现的同步性。反之,则检查模型建立是否正确。
3.2.2折减系数与路径的确定方法
强度折减法(SRM)自提出以来逐渐被认可,并随计算机技术的发展得以广泛应用。如式(2)所示SRM中黏聚力与内摩擦角的折减系数相等,也可称为“单折减”。近年来,较多学者[23-25]提出了对黏聚力、内摩擦角采用不同折减系数的“双折减法”,称为DRM。
双折减法认为强度参数c、φ在边坡发生滑动时发挥的作用不同,发挥作用的先后顺序及衰减速度也不同,采用不同的折减系数更加合理。定义双折减系数k1、k2,折减比r为
c=c/k1、tanφ=tanφ/k2(3)
r=k1/k2(4)
折减路径一般采用r控制的策略,对于SRM而言r=1,双折减法中r的确定方法一般为有限元模型中首先单对c进行折减得出Fs1,后单折减φ得出Fs2,r=Fs1/Fs2。拟定一较小的初始折减点即可确定折减路径。
经典SRM中安全系数等于折减系数,DRM安全系数Fs的确定目前有以下几种[23]。
取平均法Fs=k1+k22(5)
最小值法Fs=min[k1,k2](6)
多算例拟合法Fs=2k1k2k21+k22(7)
临界强度面积法Fs=k1k2(8)
其中,式(5)、(6)因缺乏理论依据,局限性较大,式(7)、(8)具备理论依据,说服力强。但式(7)由多组算例拟合得出,势必受数据样本影响。朱彦鹏等[26]在对4种确定式差异研究中,得出在折减比r在0.8~1.2之间时,4种确定式所得安全系数差距很小。白冰等[23]通过4个算例对DRM、SRM所得安全系数对比发现DRM所得结果均小于SRM,单折减可能高估了边坡的安全系数。算例同样表现出这一点,双折减法可作为边坡分析的新选项。此外,基于屈服状态的渐进式局部强度折减法[8]、重度折减法[27]等新兴方法同样取得了良好应用,为边坡稳定性有限元分析提供了更多思路。
3.2.3临界滑动面的搜索
边坡稳定性分析两基本要素为安全系数与滑动面位置,本文分析及其他学者的研究表明无论是极限平衡法或有限元SRM均能得到合理的安全系数,但对于滑动面位置的判断却有较大出入。滑动面位置确定法[27]主要有最小安全系数-最危险滑动面联合搜索法、基于有限元结果刻画法。前者通常采用随机搜索、遗传算法、蚁群算法、模拟退火算法及其他解最优智能算法。后者一般据有限元SRM分析结果云图,给定某种假设后进行可视化刻画。
联合搜索法首先假定滑动面,并确定滑动面安全系数表达式。复杂边坡滑动面确定较为困难,若设定任意滑动面形状,搜索算法计算量庞大存在易陷入局部最优的缺陷。基于SRM可视化结果进行滑动面的刻画则有更优的适用性。
SRM滑动面刻画准则主要有以下几种[27-30]:
(1)基于极限平衡滑动体假定,选用临界状态时位移为0等值线作为滑动面。
(2)认为滑动沿塑性区分布并起码包含塑性区,以屈服单元边界为滑动面。
(3)选取临界状态位移为某个值的等值线为滑动面。
(4)沿深度方向寻找等效塑性应变最大点,作平滑处理后作为滑动面。
(5)沿深度方向寻找位移变化率最大,即位移等值线最密集点作平滑处理作滑动面。
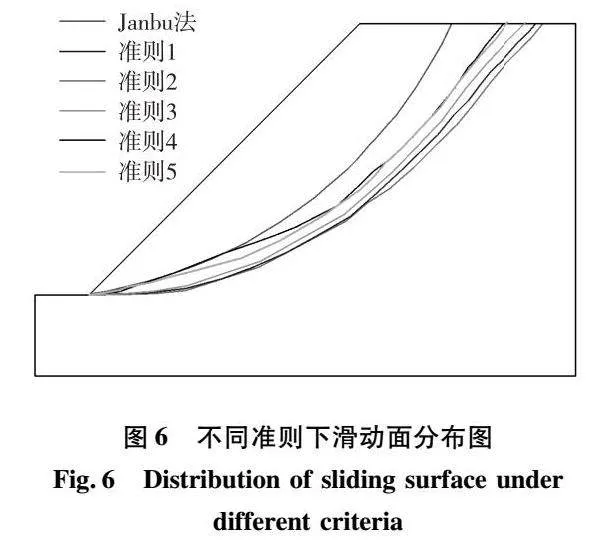
几种准则具有较强的人为性和经验性,缺乏客观、量化指标,对不同边坡的适用性及边坡内部破坏机理还应进一步探究。这里,对本文算例Abaqus软件SRM分析结果按上述5种准则刻画滑动面,由于图4所示几种极限平衡法所得滑动面相差无几,这里以Janbu法滑动面为参照进行对比,如图6所示。由图6可知Janbu法所得滑动面分布最浅,5种滑动面准则均深于Janbu法。准则1与准则2所得滑动面较为吻合,准则4与准则5所得滑动面相差不大,基于一般工程土体位移增量累计值警戒线,准则3中取位移等值线为10mm所得滑动面介于准则1、2与准则4、5之间。
本文采用Mohr-Coulomb弹塑性屈服准则,当土体一旦出现屈服则呈现理想塑性,应变趋于无限大,故准则1、2所得滑动面吻合。若与极限平衡法所得进行对比以确定合理性,本算例准则4、5最接近极限平衡法所得滑动面。基于以上分析,认为准则4或5更加合理。首先边坡失稳破坏最直观的表征为滑动体位移大于未滑动体,位移场中单位深度处位移变化率最大点连接面即位移等值线最密集处最易发生土体滑动,而后滑动面深侧土体由其自稳性位移逐渐稳定。以上分析仅基于所述算例建模结果,未进行模型试验或与实际案例监测结果对比,有效性仍待商榷。
4结论
本文采用极限平衡法与有限元强度折减法对算例均质土坡稳定性进行了分析,并从安全系数与临界滑动面两方面进行了对比。此外就目前强度折减法存在的些许问题展开了讨论,具体可得出如下结论:
1)3种极限平衡分析法(瑞典条分法、简化Bishop法、Janbu法)与2种有限元强度折减法(Midas、Abaqus)所得算例边坡安全系数处于0.89~098之间,均<1.0,算例边坡表现为失稳状态。其中,所得安全系数从小到大为瑞典条分法、简化Bishop法、Janbu法、Midas、Abaqus。瑞典条分法安全系数仅为0.89,可信度较低。故算例边坡安全系数应处于0.93~0.98。
2)3种极限平衡分析法所得临界滑动面较为吻合,不同有限元软件间采用位移云图等值线为0,刻画所得滑动面相差较大,但都深于极限平衡法。其中,Midas所得滑动面深于极限平衡法,Abaqus所得深于Midas。若按有限元SRM结果进行边坡加固,则具有更大的安全度。
3)有限元强度折减法的计算精度受模型边界条件、计算范围及网格质量等因素影响。应综合考虑等效塑性区贯通与位移突变的判据,避免单一依赖计算不收敛作为失稳判据。此外,对黏聚力与内摩擦角采用不同折减系数的“双折减法”可以更合理地反映土体强度参数的不同作用。
以上讨论说明强度折减法对于均质边坡有着较好的适用性,够直观展示边坡破坏过程,但其对于多层土边坡、岩质边坡的应用有待进一步探讨。
参考文献:
[1] 王玉平,曾志强,潘树林.边坡稳定性分析方法综述[J].西华大学学报(自然科学版),2012,31(2):101-105.
[2]张鹏.岩土边坡刚体极限平衡法的误差根源与范围研究[D].西安:西安理工大学,2003.
[3]ZIENKIEWICZOC,HUMPESONC,LEWISRW.Associatedandnonassociatedvisco-plasiticityinsoilmechanics[J].Geotechnique,1975,25(4):671-689.
[4]程灿宇,罗富荣,戚承志,等.有限元强度折减法计算边坡稳定的对比分析[J].岩土力学,2012,33(11):3472-3478.
[5]杨才,王世君,丰土根.基于塑性区开展的边坡失稳判据研究[J].中国科技论文,2016,11(13):1461-1464.
[6]王思源,童小东.基于动态强度折减-改进矢量和法的边坡稳定性分析[J].岩土工程学报,2023,45(7):1384-1392.
[7]赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座:Ⅱ有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005(2):332-336.
[8]陈国庆,黄润秋,周辉,等.边坡渐进破坏的动态强度折减法研究[J].岩土力学,2013,34(4):1140-1146.
[9]李广信.高等土力学[M].北京:清华大学出版社,2004.
[10]郑颖人,赵尚毅,时卫民,等.边坡稳定分析的一些进展[J].地下空间,2001(4):262-271,337-338.
[11]林峰,黄润秋.边坡稳定性极限平衡条分法的探讨[J].地质灾害与环境保护,1997(4):9-13.
[12]邹广电,魏汝龙.土坡稳定分析普遍极限平衡法数值解的理论及方法研究[J].岩石力学与工程学报,2006(2):363-370.
[13]杨有成,李群,陈新泽,等.对强度折减法若干问题的讨论[J].岩土力学,2008(4):1103-1106.
[14]郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002(10):57-61.
[15]赵尚毅,郑颖人,张玉芳.有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332-336.
[16]吕庆,孙红月,尚岳全.强度折减有限元法中边坡失稳判据的研究[J].浙江大学学报(工学版),2008,42(1):83-87.
[17]龙绪健,黄晓燕,张春宇,等.有限元强度折减法中的刚度退化及边坡失稳判据[J].岩土工程学报,2008,30(12):1910-1914.
[18]刘祚秋,周翠英,董立国,等.边坡稳定及加固分析的有限元强度折减法[J].岩土力学,2005,26(4):558-561.
[19]刘金龙,栾茂田,赵少飞,等.关于强度折减有限元方法中边坡失稳判据的讨论[J].岩土力学,2005,26(8):1345-1348.
[20]陈力华,靳晓光.有限元强度折减法中边坡三种失效判据的适用性研究[J].土木工程学报,2012,45(9):136-146.
[21]GRIFFITHSDV,LANEPA.Slopestabilityanalysisbyfiniteelements[J].Geotechnique,1999,49(3):387-403.
[22]王栋,年廷凯,陈煜淼.边坡稳定有限元分析中的三个问题[J].岩土力学,2007,28(11):2309-2313.
[23]白冰,袁维,石露,等.一种双折减法与经典强度折减法的关系[J].岩土力学,2015,36(5):1275-1281.
[24]唐芬,郑颖人.基于双安全系数的边坡稳定性分析[J].公路交通科技,2008,25(11):39-44.
[25]YAOHONGS.Doublereductionfactorsapproachtothestabilityofsideslopes[J].CommunicationsinComputerandInformationScience,2010,106(1):31-39.
[26]朱彦鹏,杨晓宇,马孝瑞,等.边坡稳定性分析双折减法的几个问题[J].岩土力学,2018,39(1):331-338.
[27]朱文炜,任旭华,张继勋.强度折减法与重度增加法对边坡稳定安全系数的影响[J].水电能源科学,2019,37(1):127-131.
[28]刘晓宇,赵颖,刘洋,等.土质边坡极限平衡状态及临界滑动面的判定方法[J].岩石力学与工程学报,2012,31(7):1369-1378.
[29]栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1-8.
[30]徐卫亚,肖武.基于强度折减和重度增加的边坡破坏判据研究[J].岩土力学,2007,28(3):505-511.
(责任编辑:于慧梅)
Abstract:
Inordertocomparethedifferencebetweenlimitequilibriummethodandstrengthreductionmethodinslopestabilityanalysis,throughspecificexamples,differentlimitequilibriummethodssuchasSwedishslicemethod,simplifiedBishopmethod,Janbumethodandstrengthreductionmethod(SRM)infiniteelementsoftwareareappliedtoengineeringpractice.Theslopesafetyfactorissolvedbyvariouscalculationmethods,andthestabilityresultsoftwohomogeneoussoilslopesareanalyzed.TheresultsshowthattheSwedishslicemethodhaslowreliabilityandthesafetyfactorisonly0.89.Then,theinfluenceofmeshdensityonthesafetyfactorwasdiscussedbyorthogonaltest,andtheisolineobtainedbyAbaquswasthedeepest.Inaddition,bycomparingthesafetyfactorandcriticalslipsurfaceobtainedbydifferentmethods,theproblemsofslopeinstabilityandslipsurfacesearcharefurtherdiscussed.Theresearchresultscanprovidesomereferencefortheapplicationoflimitequilibriummethodandstrengthreductionmethodinengineering.
Keywords:
strengthreductionmethod;slopestabilityanalysis;slidingsurfacesearch;numericalsimulation;orthogonaltest
收稿日期:2024-01-10
基金项目:国家自然科学基金重点资助项目(41931294)
作者简介:吴罡(1999—),男,在读硕士,研究方向:岩土工程领域,E-mail:465944013@qq.com
*通讯作者:阮永芬,E-mail:rryy64@163.com.
