一种优化均值漂移模型的测站筛选方法

文章编号1000-5269（2024）05-0026-06 DOI：10.15958/j.cnki.gdxbzrb.2024.05.04

摘要：针对均值漂移模型在异常测站剔除过程中出现的“回漂”现象导致粗差未能尽数剔除、使其拟合结果有偏于实际的问题，提出基于惩罚回归优化均值漂移模型对异常测站进行剔除的方法。利用优化后的模型方法对“中国大陆构造环境监测网络”华南块体中东部观测的水平速度场数据进行拟合对比分析，并利用剔除后的有效测站进行形变特征反演。结果表明：利用惩罚回归优化的均值漂移模型能更有效地识别异常测站点，筛选后的测站数据能顾及块体整体运动的平滑性，同时比均值漂移模型剔除具有更高的拟合精度，利用有效数据反演的形变特征也符合该区域实际运动趋势。

关键词：地壳运动；异常测站；均值漂移模型；惩罚函数；应变特征 中图分类号：P227；P313 文献标志码：A

任何观测结果都会包含噪声，全球卫星定位导航系统（GlobalNavigationSatelliteSystem，GNSS）监测站在地壳形变速度场连续观测中也8d826b8fce9328f3fba0a6b89d931f199c06d2a64435f34a68f90616a1d1d818不例外。监测站点可能会受到局部干扰或局部构造形变的影响，使同一块体上的监测站点有时会表现出不协调的位移［1］。人们把这类不协调位移的测站定义为异常测站。这类测站的存在会影响地壳运动模型拟合的精度和可靠性。所以，必须对监测站速度场数据进行合理有效的筛选，并对异常测站进行剔除。异常测站剔除的过程究其原理，可视为粗差的探测及定位，常用的方法是以最小二乘法为基础将粗差归为函数模型，利用两倍中误差法、拟准检定法、均值漂移模型等方法进行探测。文献［2］利用两倍中误差法、拟准检定法、均值漂移模型进行测站筛选对比，得出均值漂移抗差估计模型剔除效果明显好于拟准检定法和两倍中误差法。而均值漂移量的搜索方向无法进行限制，容易出现“回漂”现象［3］，导致粗差剔除不完整。针对此问题，本文提出利用平滑剪切绝对偏差（smoothlyclippedabsolutedeviation，SCAD）惩罚函数对均值漂移模型异常测站剔除方法进行优化，对“中国大陆构造环境监测网络”在华南块体的GNSS观测的速度场数据进行筛选，并对筛选出的有效速度场数据进行拟合分析。结果表明：此方法能有效识别异常测站点，一定程度上克服了“回漂”影响，利用优化的均值漂移模型筛选的测站数据进行拟合具有更高的拟合精度。

1测站剔除的方法

1.1基于刚性运动的地壳形变模型

传统的块体运动模型不考虑块体内部形变，将块体水平运动视为绕欧拉轴的有限旋转运动，其模型为［4-5］

VEVN=r-cosλsinφ-sinλsinφcosφsinλ-cosφ0ωxωyωz（1）

式中：VE表示板块任意一点在东西方向的运动速率，VN表示南北方向的运动速率；r是地球平均半径；λ为大地经度，φ为大地纬度；ωx，ωy，ωz定义为欧拉旋转参数。相应欧拉极参数计算公式为

ω=ω2x+ω2y+ω2zl=atan（ωyωx）φ=atan（ωzω2x+ω2y）（2）

式中：ω为欧拉经度；l为欧拉纬度；φ为旋转角。利用式（1）对速度场数据进行拟合处理，利用观测值与拟合值求差，得出速率残差值，其服从正态分布，符合随机误差特性，因此利用两倍中误差作为阈值进行测站筛选是合理的方法，但其模型本身未能顾及块体整体位移的平滑性，从而导致剔除效果减弱。

1.2基于均值漂移模型的测站筛选［6-7］

将式（1）简化为测量平差问题的Gauss-Markov模型

L=AX+ΔΔ～Nn（0，σ20P-1）（3）

设未知参数向量估值为X^，L为观测值向量，V=AX^－L为误差方程，则最小平差解为X^=（ATPA）-1ATPL。设可靠性矩阵为R=I－A（ATPA）－1ATP，且RL=－V。假设第i个观测值存在异常，则含有粗差的均值漂移模型为

L=AX+r+ΔΔ～Nn（0，σ20P-1）r=（0，…，ri，…，0）（4）

式中：ri为漂移量。根据最小二乘法得出均值漂移模型的抗差估计的解：

X^=（ATPA）-1ATP（5）

式中：为等价观测值。

利用迭代法求出未知参数解，即

X^k+1=（ATPA）-1ATPk+1（6）

观测值迭代抗差解计算表达式可表示为

k+1=k－rk，rk=（rk1，…，rkn）

rki=0，k－1i≤c

rk-1i，k－1i>c（7）

式中：k－1i为第k－1步的标准化残差，c值视实际情况而定，一般取值范围在0～3。rk－1i为rk－1=-（diag（R））－1k－1的第i个分量，diag（R）表示R的对角矩阵，k－1=k－1－AX^k－1。若观测值无粗差影响，则RL=－V且V很小；若观测值中含有粗差，设R（L+r）=－，r为异常值，则有Rr－V=-，又因为V相比于很小且R－1≈0，故r=-（diag（R））－1，此时粗差值便可定位。利用均值漂移模型剔除异常测站具体步骤见文献［2］。

1.3基于SCAD惩罚回归的测站筛选［8-10］

由式（4）确定的异常值识别量r是稀疏的，因此在利用上述方法检测异常测站时容易出现“回漂”现象，故利用SCAD惩罚函数对其漂移量施加惩罚，得到的目标函数如式（8）：

FnX，r;λn=‖Y－AX－r‖22+n∑ni=1Pλnri（8）

式中：‖·‖2为l2范数；∑ni=1Pλn（ri）为惩罚函数项;n为样本数量，即观测站数;λn>0是惩罚函数中的阈值参数。

由文献［9］可知，SCAD惩罚函数可通过局部线性近似拟合，即Pλn（x）≈P′λn（x^（0））x，x^（0）为x的初始估计量，P′λn（x）为Pλn（x）的一阶导数，定义如式（9）：

P′λn（x）=λnI（x≤λn）+（aλn－x）+（a－1）λnI（x>λn）（9）

式中：x>0，a>2，I（·）为示性函数，（aλn-x）+=max（0，aλn-x）。利用式（9）对式（8）进行拟合后可得加惩罚的目标函数如式（10）：

Fn（X，r;λn）=‖Y-AX-r‖22+n∑ni=1P′λn（r^（0）i）ri（10）

式中：（0）i为ri的初始估计值，X和r的估计量如式（11）。

（X^，r^）=argminLnX∈Rp-1，Δ∈Rn（X，r;λn）（11）

基于SCAD惩罚函数优化的均值漂移模型的参数解算采用坐标下降法，解算步骤如下：

第1步：设置初始值（X^（0），r（0）），令k=1。

第2步：令r（k）=argminHn（X^（k－1），r；λn1，λn2），利用公式（12）确定惩罚函数Hn的最小值，并设定r^（k）=（r^k1，…，r^kn）T，令i=1，…，n。

r^（k）i=argminHn（X^（k－1），（r^k1，…，r^ki-1，ri，r^（k-1）i-1）T;λn1，λn2）

（12）

第3步：令X^（k）=argminHn（X，r^k；λn1，λn2），利用公式（13）确定惩罚函数Hn的最小值，并设定X^（k）=（X^k0，…，X^kn）T，令j=1，…，p。

X^（k）i=argminHn（（X^k0，…，X^kj-1，Xj，X^（k-1）j-1，…，X^（k-1）p）T，r^（k）;λn1，λn2）

（13）

第4步：令k=k+1，重复第2步和第3步，直至漂移量为0，即为正常测站，不为0的为异常测站，剔除。

2测站剔除及形变特征分析

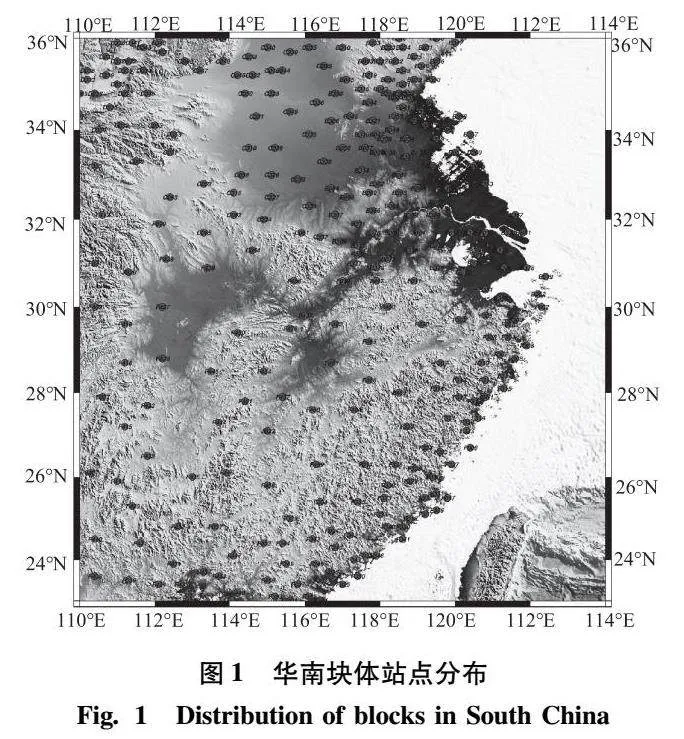
本文采用1998—2014年间“中国大陆构造环境监测网络”观测的华南块体水平速度场数据，通过解算得到的华南块体中东部地区在ITRF2008框架下统一速度场数据精度优于2mm/a，该区域监测站分布及水平速度场如图1、图2所示［11-12］。从图2可以看出，此区域常年运动区域稳定，以6.783mm/a的速度向东移动，故以刚性运动模型为基础进行测站筛选。

为验证本文方法，用以下3种方法对异常测站进行剔除：

方案Ⅰ：利用块体的刚性运动模型对未进行筛选的水平速度场数据进行拟合分析。

方案Ⅱ：利用均值漂移模型对异常测站进行剔除，用块体的刚性运动模型对有效数据进行拟合分析。

方案Ⅲ：利用惩罚回归优化的均值漂移模型对异常测站进行剔除，用块体的刚性运动模型对有效数据进行拟合分析。

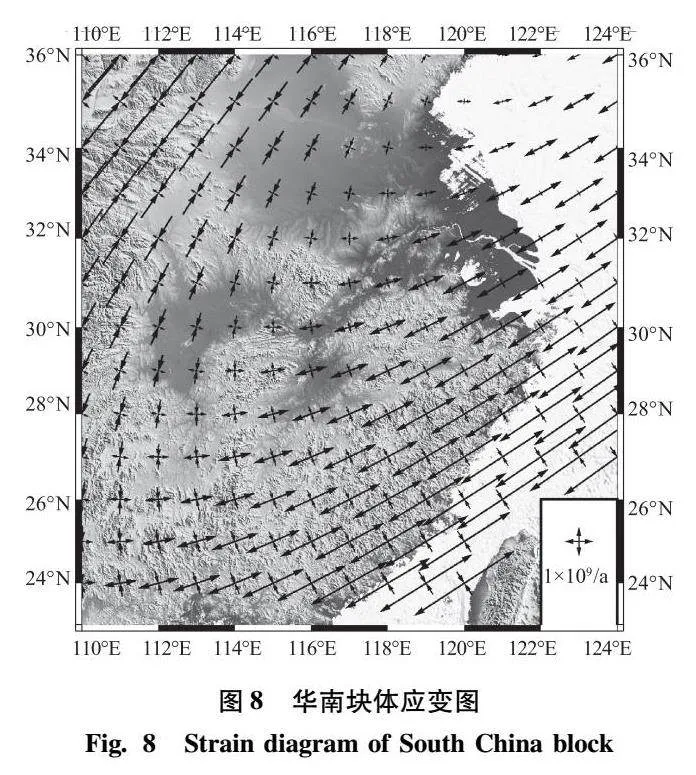
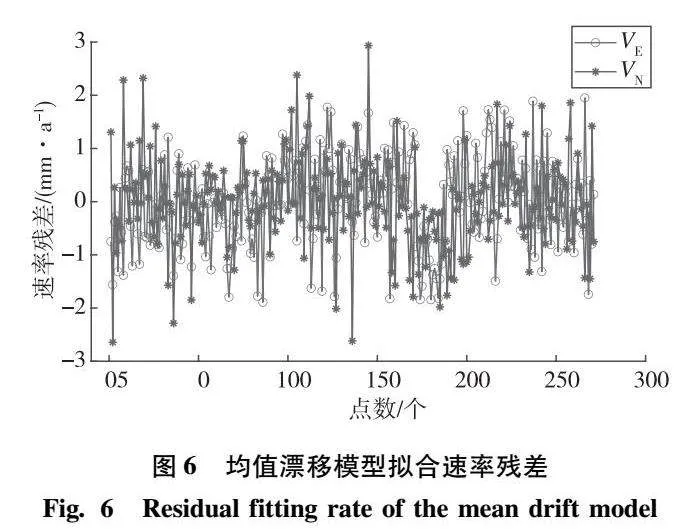
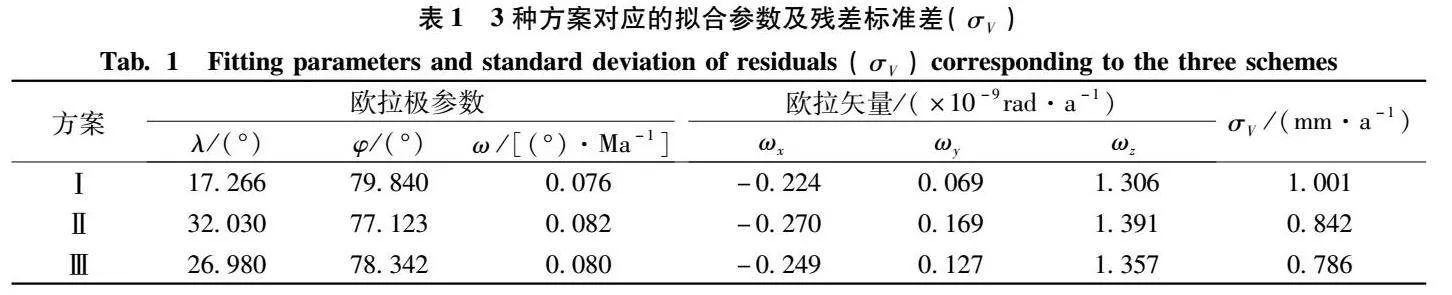
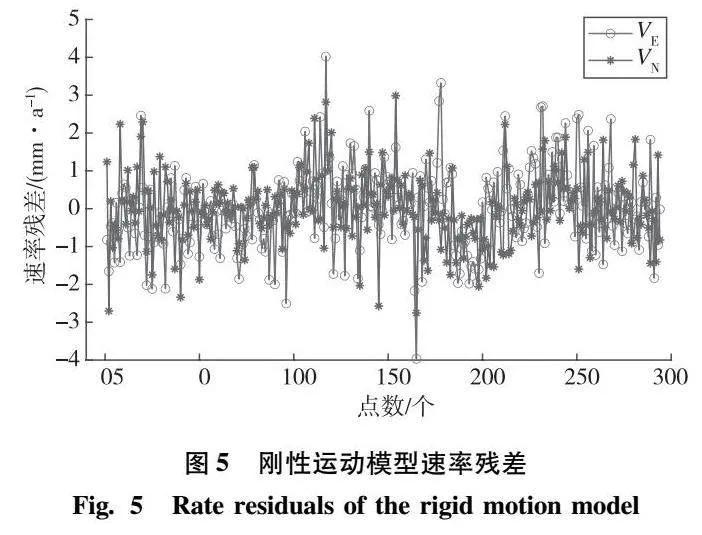
3种方案的拟合结果列于表1，同时给出方案Ⅱ和方案Ⅲ各自的异常测站分布点图及速率残差，见图3—图7；利用块体线性应变模型对方案Ⅲ拟合的结果进行应变特征反演，如图8所示。

由计算结果得出如下分析：

1）利用方案Ⅱ、方案Ⅲ对异常测站进行剔除，应剔除的异常测站点数分别为23和31。从图3、图4可以看出：优化后的均值漂移模型剔除的异常测站分布与未优化前相比多剔除了8个；但在分布上，与均值漂移模型保持一致，间接证明了利用惩罚回归剔除异常测站的可行性。

2）从图5、图6、图7可以看出：利用未进行异常测站剔除的速度场的速率残差在东西方向和南北方向最大值均在4mm/a左右，未经优化的均值漂移模型剔除异常测站后的拟合结果显示在东西方向最大为2.7mm/a，南北方向上的速率残差最大值为3mm/a，而经惩罚函数优化后的均值漂移模型剔除异常测站后的拟合结果显示在东西方向和南北方向上的速率残差最大值均在2mm/a左右；对比方案Ⅱ、方案Ⅲ，无论从东西方向还是从南北方向的拟合，方案Ⅲ残差最大值均小于方案Ⅱ；从表1中的速率残差标准差可以看出方案Ⅰ未经测站剔除的拟合精度最差，方案Ⅲ剔除后拟合精度最优；另外，利用方案Ⅲ解算的欧拉参数值和欧拉矢量值最趋近于方案Ⅰ，即趋近于未进行异常测站剔除的拟合结果，更好地说明方案Ⅲ更能顾及块体整体运动的平滑性。综上所述，无论是从速率残差残差图对比，还是从残差标准差及解算参数的对比，方案Ⅲ对异常测站剔除的效果最优，即利用惩罚回归优化的均值漂移模型对速度场数据处理的效果更好。

3）从图8可以看出，华南块体中东部地区存在不同程度、不同方向的压缩和扩张。其主压应变从西至东逐渐减弱，由南北方向按逆时针转动；其主张应变从西至东、从北至南逐渐扩大，从北至南呈顺时针方向转动，此结果与张静华、李延兴等的研究结果大体一致［13］。从研究区域地理位置分析，该区域所处欧亚板块，受印度板块挤压，整体向东移动；另外，该区域北边界还受到华北块体挤压，南边界受到南海块体自南向北的推挤力；在东南方向受到菲律宾海板块向西北方向的仰冲作用力。因此，内部形变变化复杂。由此可见，图8反演结果接近于实际。

3结论

GNSS测站的筛选与剔除是研究地壳形变时不可缺少的重要环节。本文针对GNSS的对地观测速度场数据出现的异常测站，提出利用SCAD惩罚函数改进均值漂移模型的抗差估计对异常测站进行剔除的方法。均值漂移模型虽然能有效地检测粗差位置，但不可避免地会出现“回漂”现象，而SCAD惩罚函数改进的均值漂移模型能更准确地解决线性模型数据中异常值的检测问题，在一定程度上克服了一般方法未能克服的隐差现象及均值漂移模型的“回漂”现象，对后续地壳形变模型的拟合、块体应变反演的精度大有提升，也为地壳形变异常测站的剔除提供了一种新的思路。

参考文献：

[1]

李亚萍，孙付平，朱新慧，等.抗差主成分估计在板块运动参数解算中的应用［J］.测绘工程，2016，25（8）：38-41.

［2］范成成，张俊，雷前坤，等.均值漂移模型在地壳运动异常测站剔除中的应用［J］.测绘通报，2020（5）：80-84.

［3］高向东，黎扬进，刘秀航，等.改进均值漂移算法的焊缝特征点识别分析［J］.华南理工大学学报（自然科学版），2019，47（4）：132-137.

［4］李延兴，黄珹，胡新康，等.板内块体的刚性弹塑性运动模型与中国大陆主要块体的应变状态［J］.地震学报，2001，23（6）：565-572.

［5］王东东.基于GPS速度场的地壳弹塑性形变模型及应用［D］.贵阳：贵州大学，2018：6-7.

［6］张探探，樊亚莉，钟先乐.基于均值漂移模型的异常值检测方法［J］.上海理工大学学报，2018，40（2）：116-120.

［7］范成成.顾及先验信息的地壳形变分析模型研究［D］.贵阳：贵州大学，2020：12-13.

［8］ZOUH，LIRZ.One-stepsparesestimatesinnonconcavepenalizedlikelihoodmodels［J］.AnnalsofStatistics，2008，36（4）：1509-1533.

［9］潘莹丽，刘展，宋广雨.基于SCAD惩罚回归的异常值检测方法［J］.统计与决策，2022，38（4）：38-42.

［10］万超.基于SCAD稀疏约束的字典学习算法及其在信号处理中的应用［D］.广州：广东工业大学，2021.

［11］ZHAOB，HUANGY，ZHANGCH，etal.CrustaldeformationontheChinesemainlandduring1998—2004basedonGPSdata［J］.GeodesyandGeodynamics，2015，6（1）：7-15.

［12］石玉涛，高原.华南块体中部上地壳剪切波分裂特征［J］.地球物理学报，2022，65（9）：3268-3279.

［13］张静华，李延兴，郭良迁，等.华南块体的现今构造运动与内部形变［J］.大地测量与地球动力学，2005（3）：57-62.

（责任编辑：曾晶）

Abstract：

Inviewoftheproblemthatthe“backdrift”phenomenonofthemeandriftmodelintheprocessofanomalousstationexclusionleadstothefailuretoeliminateallthegrosserrors，andthefittingresultsarebiasedtoreality，amethodofeliminatingabnormalstationsbasedonpenaltyregressionoptimizationmeandriftmodelisproposed.TheoptimizedmodelmethodwasusedtofitandcomparethehorizontalvelocityfielddataobservedinthecentralandeasternpartsoftheSouthChinablockbythe“Chinesemainlandtectonicenvironmentmonitoringnetwork”，andthedeformationcharacteristicswereinvertedbyusingtheeffectivestationsafterelimination.Theresultsshowthatthemeandriftmodeloptimizedbypenaltyregressioncanidentifyabnormalstationsmoreeffectively，andthefilteredstationdatacantakeintoaccounttheoverallmotionsmoothnessoftheblockandhaveahigherfittingaccuracythanthemeandriftmodel.Thedeformationcharacteristicsinvertedbyusingeffectivedataalsoconformtotheactualmovementtrendoftheregion.

Keywords：

crustalmovement;anomalystation;meanshiftmodel;penaltyfunction;straincharacteristics

收稿日期：2023-10-08

基金项目：贵州省青年科技人才成长项目（黔教合KY字［2022］132号，黔教合KY字［2022］135号）；贵州工程应用技术学院一流专业建设项目（ZY202104）

作者简介：范成成（1995—），男，讲师，硕士，研究方向：板块运动及地壳形变分析理论，E-mail：970864235@qq.com.

*通讯作者：范成成，E-mail：970864235@qq.com.