伏牛山区栓皮栎天然次生林径级结构模型研究

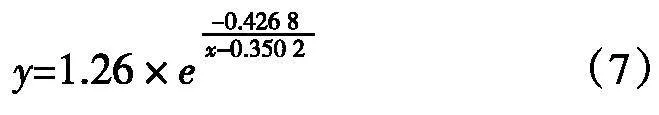
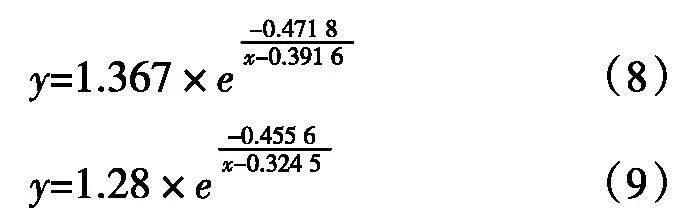
摘要： [目的]以伏牛山区栓皮栎天然次生林为研究对象，探索其径级结构变化规律，建立了神经网络径级分布模型，为伏牛山区栓皮栎天然次生林合理经营提供理论基础。[方法]采用人工神经网络建模技术和数学函数法建立伏牛山区栓皮栎天然次生林径级分布模型， [结果]（1）随着坡位变换伏牛山区栓皮栎天然次生林径级分布类型不同，上坡为反J形分布，中坡为正态分布，下坡为单峰左偏分布。（2）建立了不同坡位的神经网络径级分布模型，拟合精度分别为0.997 9、0.994 3、0.995 9。（3）负指数函数能较好地拟合栓皮栎天然次生林径级分布，不同坡位拟合精度分别为0.952 7、0.959 4、0.964 1。 [结论] 林分生长具有非线性和复杂性，而人工神经网络具有拟合任意非线性的能力，并且不受树种、立地条件、气候等因素影响。

关键词： 伏牛山区； 栓皮栎； 天然次生林； 神经网络； 径级

中图分类号： S 757 文献标识码： A 文章编号：1001 - 9499（2024）05 - 0006 - 05

DBH Class Structure of Quercus variabilis Natural Secondary Forest in Funiu Mountain

Abstract [Objective]In this study， the DBH class structure of Quercus variabilis natural secondary forest in Funiu mountainous were explored， and the DBH class distribution model based on ANN in order to provide theoretical basis for reasonable management of Quercus variabilis natural secogaAhokOoIlpaH6PXKBpRaC9Buo/oNuftS94BSeCNJ5Y=ndary forest in Funiu mountainous. [Method] The diameter distribution model in the study area were established by the application of ANN and mathematical function. [Result]（1）The types of diameter distribution Quercus variabilis natural secondary forest in the Funiu area were different as the slope changed， the diameter distribution of uphill was in a reverse J-shape， the middle slope was normally distributed， downhill was single peak left deviation.（2）The diameter distribution model of different slope position were established based on ANN， whose fitting precision respectively reached 0.952 7、0.959 4 and 0.964 1.（3）The diameter distribution of natural secondary forests of Quercus variabilis were better fitted by negative exponential function， whose fitting accuracy were separately 0.952 7、0.959 4 and 0.964 1 in different slope position. [Conclusion] Forest growth has nonlinearity and complexity， while ANN has the ability to fit any nonlinearity and is not affected by factors such as tree species， site conditions and climate， etc. In the Funiu Mountain， Quercus variabilis is a constructive species below an altitude of 1 000 m， whose carbon density increases with increasing altitude. The carbon density on sunny slopes is higher than that on shaded slopes due to the factors such as site environment and tree species characteristics.

Key words Funiu mountain; Quercus variabilis; natural secondary forest; ANN; diameter class

森林是陆地生态系统的主体，是地球生物圈的重要组成部分[ 1 ]。全国森林面积中，天然林占63.55%，但天然林蓄积占总蓄积的80.14%[ 2 ]。天然林在发挥森林生态服务价值方面发挥着主要作用。栎类是河南主要树种之一，现在多为天然萌生次生林，存在林分密度大、干形弯曲、材质差等问题，森林生产力不高，针对栎类天然次生林开展研究非常必要。

合理的林分结构是充分发挥森林生态服务功能的基础[ 3 ]。林分结构指林分内部特征因子的分布状态[ 4 ]，径级分布是最基本的林分结构[ 3 ]。根据森林生长理论，林分生长将导致径级分布发生变化，而径级分布反过来决定着林分的生长[ 5 ]。以往多采用数学函数方法研究径级分布，如三参数Weibull分布、幂函数法、负指数函数法，这种方法存在的普遍问题是模型简单、多次迭代，降低了拟合的准确性。林分生长是一种复杂的非线性过程，采用数学函数拟合是将复杂的问题简单化了。本研究采用人工神经网络技术拟合林分径级分布，与传统数学函数相比，人工神经网络具有无限逼近任意非线性的功能[ 6 ]，非常适合拟合林分生长过程。以伏牛山区栓皮栎天然次生林为研究对象，探索其径级结构变化规律，建立了神经网络径级分布模型，以期为伏牛山区栓皮栎天然次生林合理经营提供理论基础。

1 材料与方法

1. 1 研究区概况

研究区位于河南省伏牛山区，伏牛山区面积占河南省山地丘陵面积的40%，属于北亚热带和暖温带的分区线，垂直气候变化明显，植被资源丰富。海拔500～2 000 m，年均温12.1～12.7 ℃，日平均气温≥10 ℃的天数为187～197 d，积温3 500～3 700 ℃，年降水量600～850 mm，主要在6～8月，占全年降水量的48%左右。伏牛山区植物种类极其丰富，建群种主要有有栓皮栎、锐齿栎、华山松、油松等。

1. 2 样地设置

伏牛山区栓皮栎天然次生林主要分布在海拔500～1 000 m内， 2021年选取调查92块20 m×30 m的栓皮栎天然次生林标准地，标准地优势树种为栓皮栎。采用生长锥钻取标准木木芯法确定林分年龄，92块标准地林龄均属中幼龄林。标准地内林分密度、乔木层调查树种名称、胸径、树高、冠幅、生活力等（表1）。

1. 3 数据可行性分析

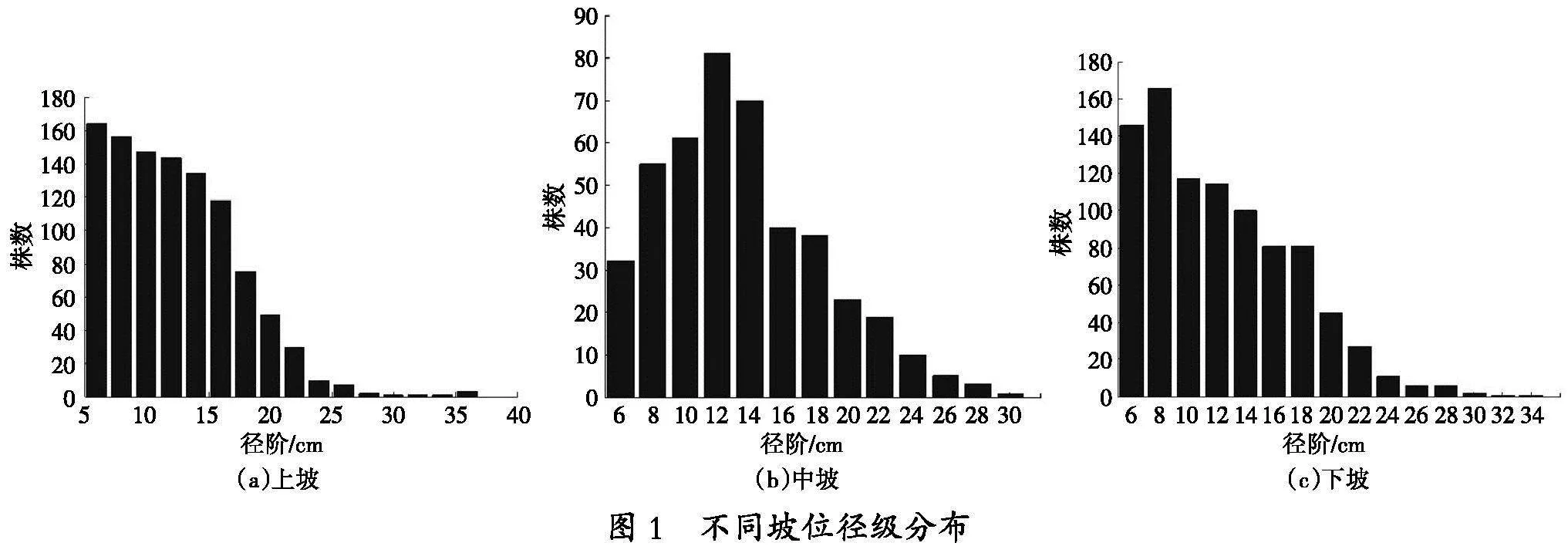
调查所用栓皮栎天然次生林标准地，栓皮栎占树种组成的8成以上，符合相对纯林的概念。为进一步探索林分类型，将所用调查数据分上、中、下不同坡位进行统计，并做径阶分布图（图1）。

由图1可知，不同坡位径级分布类型有差异，上坡（A）林分小径级林木株数最多，随着直径增大，林木株数逐渐减少，直径达18 cm后林木株数锐减，28 cm后株数趋于稳定，曲线类型呈现典型的反J形曲线。中坡（B）为单峰山状曲线，峰点为林分算术平均直径12.8 cm，中等大小的林木株数占多数，两端径阶林木株数逐渐减少，曲线类型符合截尾正态分布。下坡（C）林分类型峰点在8 cm左右，但林分算术平均直径为11.9 cm，曲线类型为不对称的单峰分布类型。

为检验中坡（B）是否为正态分布，调用MATLAB工具箱中的normfit函数，函数式

[μ，σ， muci， sigmaci]=normfit（N，0.05）（1）

式中，μ为总体均值的最大似然估计；σ为总体标准差的最大似然估计；muci为总体均值的95%的置信区间；sigmaci为总体标准差95%的置信区间。

由表2可知，不同坡位的总体均值最大似然估计值和总体标准差最大似然估计值均落在其相应的置信区间内。由图1、表2定性与定量分析相结合，可知中坡林分分布类型符合正态分布。

由上述分析可知，虽然不同坡位林分分布类型各不相同，但均表现出较为稳定的林分结构规律。本研究在探索林分结构规律的基础上，选择合适的数学函数建模，为进一步研究森林经营技术提供依据。

1. 4 模型构建思路

本研究以径阶上限相对直径作为输入变量，以径阶株数累积频率作为输出变量构建林分直径分布神经网络模型，相应的数学模型如式（2）。采用均方根误差和拟合精度等参数检测模型优劣。

y=Purelin（∑w1i2logsig（w1i1x+bi1）+b2）（2）

式中，y为径阶株数累积频率；x为相对直径；Purelin为MATLAB软件中的直线函数；w1i2为神经网络输出层权值；logsig为MATLAB软件中的曲线函数；w1i1为神经网络输入层权值；bi1为输入层阈值；b2为输出层阈值。

为便于比较，依据不同坡位径级分布规律，选择适应能力较好的数学函数， Weibull函数如式（3）、双曲线函数如式（4）、负指数函数式（5）、Logistic曲线函数模型如式（6）做比较。采用残差平方和、均方根误差做检验。

y=abxb-1e-αx （3）

y=（x+a）/（bx+c）（4）

y=αeb/（x+c）（5）

y=a/（1+be-（x+c））（6）

式中，y代表株数累积频率；x为相对直径；a、b、c分别代表模型参数。

2 结果与分析

2. 1 神经网络建模结果

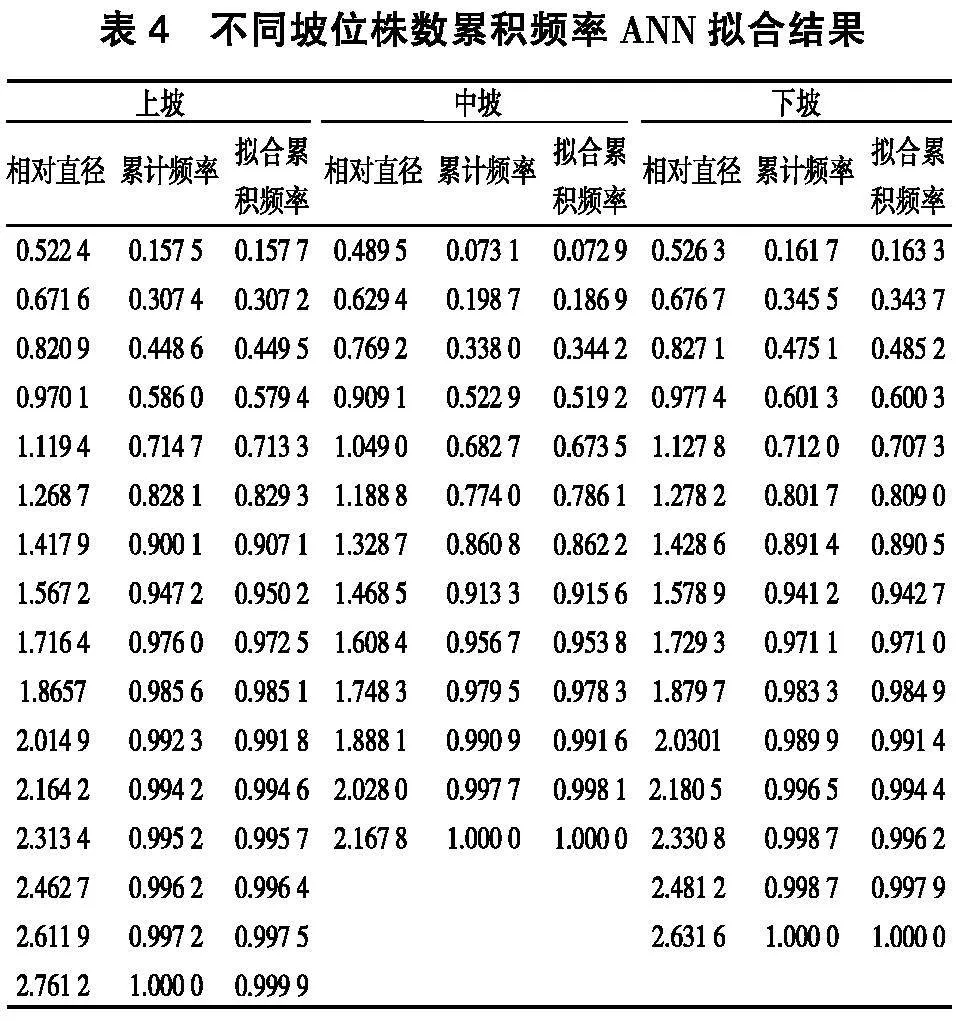
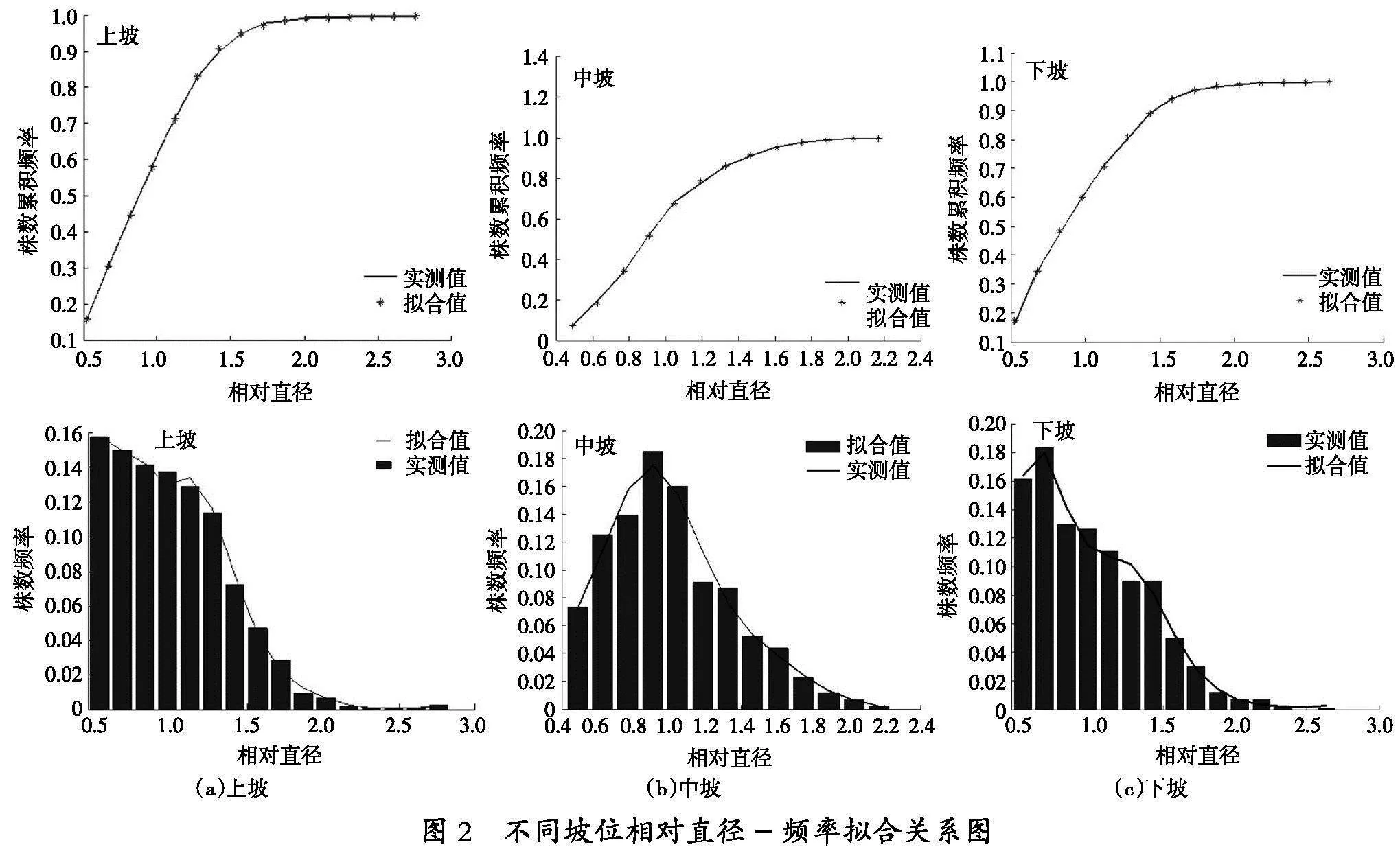
以相对直径为输入变量，以株数累积频率为输出变量，用伏牛山区不同坡位栓皮栎天然次生林为样本数据对所构建的神经网络模型进行反复训练，得到相应模型参数，对应函数表达式如表3。拟合结果如表4所示，拟合曲线如图2所示。

表3中函数表达式参数包含了所选神经网络结构的所有权值和阈值矩阵，上、中、下三个坡位的拟合精度均达到了0.99以上，均方根误差也很小。由对照表4可以看出，不同组别实测值与拟合值相差不大，神经网络能较好地拟合林分生长变化。因神经网络有无限逼近任意非线性的功能，为避免神经网络在建模时出现过度拟合，需采用定性与定量相结合的办法。由图2可知，拟合值均匀地分布在实测曲线上下两侧，拟合曲线呈“S”形，符合林分生长的一般规律。

2. 2 数学函数建模结果

选择有较好适应能力的数学函数，包括Weibull函数、双曲线函数、负指数函数、Logistic曲线函数作为基本函数，采用伏牛山区栎类天然次生林为样本数据进行拟合。

由表5可知，用残差平方和与均方根误差最小为检测指标，采用不同数学函数进行拟合时，不同坡位均表现为负指数函数拟合效果最好。同时，不同坡位，负指数函数的拟合精度也是最高的，分别达到了0.952 7、0.959 4、0.964 1。上、中、下三个坡位负指数函数关系表达式：

3 结 论

本研究采用定性与定量相结合的方法研究伏牛山区不同坡位栓皮栎天然次生林径级分布，发现伏牛山区不同坡位径级分布各不相同，上坡为典型的反J型分布，中坡为截尾正态分布，下坡为单峰左偏分布。不同坡位中小径阶林木株数较多，林分更新状态良好。上坡和下坡6～16 cm径阶株数均达到了80%以上，所调查林分属于中幼龄林。

受多种因素影响，林分的生长过程具有非线性和复杂性。人工神经网络具有无限逼近任意非线性的能力，非常适合对林分生长过程进行拟合。本研究采用人工神经网络建模技术，以伏牛山区不同坡位栓皮栎天然次生林调查数据为依据，通过不断变换神经网络结构，反复训练，得到不同神经网络结构的权值和阈值矩阵。在均方根误差最小、拟合精度最高、拟合曲线符合林分生长规律等度量标准上，选择理想的神经网络模型结构。上坡神经网络模型结构为1∶4∶1、中坡模型结构1∶2∶1、下坡模型结构1∶3∶1，不同坡位拟合精度依次为0.997 9、0.994 3、0.995 9，拟合精度较高。

为便于比较，采用相同的调查数据对具有较好拟合效果的数学函数，包括Weibull函数如式、双曲线函数如式、负指数函数式、Logistic曲线函数进行拟合，并求解模型参数。研究结果表明负指数函数在拟合不同坡位栓皮栎天然次生林径级分布上具有较好的拟合效果。上、中、下不同坡位拟合精度分别达到了0.952 7、0.959 4、0.964 1。

关于林分径级结构的研究已有很多，学者们发现，受地形、水热、林分种类等因素影响，不同树种径级分布适用不同的数学函数。惠刚盈等[ 7 ]认为Logistic函数拟合杉木人工林效果最好。杨锦昌[ 8 ]认为Richards函数拟合黄藤人工林效果最好。易烜等[ 9 ]认为Weibull函数拟合栓皮栎天然次生林效果更好。人工神经网络具有拟合任意非线性的能力，不受树种、立地条件、气候等因素影响。本研究采用人工神经网络建模技术和传统数学函数相比较，发现人工神经网络在伏牛山区不同坡位栓皮栎次生林径级分布中拟合精度均远高于负指数函数。

参考文献

［1］ 葛立雯， 潘刚， 任德智， 等. 西藏林芝地区森林碳储量、碳密度及其分布［J］. 应用生态学报， 2013， 24（2）： 319 - 325.

［2］ 国家林业和草原局. 2014-2018中国森林资源报告［M]］. 北京： 中国林业出版社， 2019.

［3］ 罗也， 王君， 杨雨春， 等. 胡桃楸次生林径级结构及乔木生物量研究［J］. 北京林业大学学报， 2022， 44（1）： 29 - 37.

［4］ 孟宪宇. 测树学［M］. 北京： 中国林业出版社， 2006.

［5］ 黄家荣. 森林生长的人工神经网络建模［M］. 北京： 中国农业出版社， 2006.

［6］ 刘光武， 陈晨， 王柯力. 基于神经网络的马尾松人工林密度指数模型［J］. 浙江农林大学学报， 2020， 37（1）： 100 - 104.

［7］ 惠刚盈， 盛炜彤. 林分直径结构的研究［J］. 林业科学研究，1995， 8（2）： 127 - 131.

［8］ 杨锦昌. 单叶省藤和黄藤人工林的系统经营技术［D］. 北京： 中国林业科学研究院， 2004.

［9］ 易烜， 朱光玉， 王琢玙， 等. 栎类天然次生林直径结构规律初探［J］. 中南林业调查规划， 2021， 40（1）： 49 - 55.