考虑土体参数不确定性的新型挡土墙可靠性分析







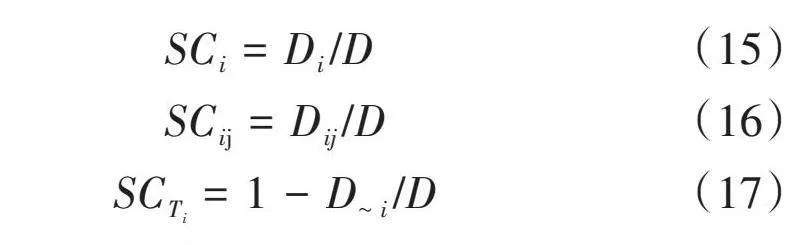
摘 要:【目的】为克服新型挡墙稳定性安全评估中传统确定性分析存在的缺陷,需要对考虑土体参数不确定性的新型挡土墙可靠性进行分析。【方法】首先,通过概率分布表达岩土参数的不确定性,计算新型挡墙的抗倾稳定和抗滑稳定。其次,通过神经网络和蒙特卡罗模拟,执行新型挡土墙可靠性分析,定量给出新型挡土墙可靠性指标。最后,通过参数敏感性分析,明确各参数对新型挡土墙安全性影响的重要程度。【结果】结果表明,新型挡土墙稳定性好,但存在一定优化空间,确定性分析结果较为保守。【结论】不同参数对新型挡土墙安全影响各不相同,应准确估计填土内摩擦角,保证挡土墙稳定性。研究成果为新型挡土墙可靠性分析提供了思路和方法。
关键词:新型挡土墙;参数不确定性;可靠性分析;敏感性分析
中图分类号:P642.22;TV221.2 文献标志码:A 文章编号:1003-5168(2024)15-0046-04
DOI:10.19968/j.cnki.hnkj.1003-5168.2024.15.010
Reliability Analysis of a New Retaining Wall Considering Soil
Parameter Uncertainty
XU Haolun1 ZHANG Yingxue 2
(1.Chongqing Water Conservancy and Electric Power Construction Survey,Design and Research Institute Co., Ltd., Chongqing 404100,China; 2. Chongqing 208 Geological Environment Research Institute Co., Ltd., Chongqing 404100,China)
Abstract: [Purposes] In order to overcome the shortcomings of the traditional deterministic analysis on the stability safety assessment of the new retaining wall, it is necessary to analyze the reliability of the new retaining wall considering the uncertainty of soil parameters.[Methods] Fristly, this paper expresses the uncertainty of soil parameters through probability distribution and calculates the overturning stability and sliding stability of the new retaining wall. Secondly,through neural networks and Monte Carlo simulations, reliability analysis of the new retaining wall is performed, providing quantitative reliability indicators. Finally, through parameter sensitivity analysis, the importance of each parameter on the safety of the new retaining wall is clearly identified. [Findings] The results indicate that although the new retaining wall has good stability, there is room for optimization, and the deterministic analysis results are conservative. [Conclusions] Different parameters have varying impacts on the safety of the new retaining wall. Accurate estimation of the internal friction angle of the backfill soil should be ensured to guarantee the stability of the retaining wall. The research approach of this paper provides ideas and methods for the reliability analysis of the new retaining wall.
Keywords: new retaining wall; parameter uncertainty; reliability analysis; sensitivity analysis
0 引言
挡土墙是水利工程中常用的支挡结构,其中重力式挡土墙应用最为广泛。由于重力式挡土墙特殊的受力特性,其存在材料用量大、施工周期长、经济性欠佳等缺点。而装配式挡土墙造价低、自重小,预制化生产也缩短了施工周期,符合低碳环保的设计理念。因此,装配式挡土墙是一种具有竞争力的挡土结构[1]。
挡土墙与土体联合结构安全问题备受关注。工程上通过安全系数来衡量挡土墙安全性,简单且易操作。然而,安全系数大于1并不意味着挡土墙不发生失效。因为天然土体在风化、沉降、侵蚀等综合作用下,土体性质随着空间位置的变化存在一定的随机性,这种随机性为挡土墙安全性评估带来了极大不确定 [2]。为合理表征土体特性的不确定性,可靠性设计弥补了确定性计算方法的缺陷,对指导新型装配式挡土墙设计有着重要意义[3]。
1 研究方法与理论
1.1 新型装配式挡土墙的构造
根据具体工程需求,对预制块的形状进行选择,通常采用仰斜式构造形式[1]。挡土墙墙背采用预制块错位的堆叠方式,预制块内部通孔,形成贯通通道。在通孔中加入钢筋后注入砂浆,形成整体的挡土墙结构,以提高挡土墙整体抗拉性能和整体稳定性。
1.2 挡土墙稳定分析及确定性计算
本研究开展挡土墙结构稳定性分析,包括整体抗滑稳定计算、体抗倾覆计算以及墙体基底压力验算。倾斜式墙背挡土墙,墙背填土采用非黏性土进行回填。本研究采用库伦土压力公式计算墙背土压力、主动土压力,见式(1)、式(2),被动土压力见式(3)、式(4)。
[Ka=cos2(φ-ε)cos2εcos(φ+δ)+[1+sin(φ+δ)(φ-β)cos(φ+δ)cos(ε-β)]2] (1)
[Fa=12γH2Ka] (2)
[Kp=cos2(φ+ε)cos2εcos(φ-δ)+[1-sin(φ+δ)(φ+β)cos(ε-δ)cos(ε-β)]2] (3)
[Fa=12γH2Kp] (4)
式(2)、式(3)中系数Ka和Kp分别为被动土压力系数和主动土压力系数。
本研究以抗倾覆稳定、抗滑稳定为研究对象,抗倾稳定安全系数、抗滑稳定安全系数的计算见式(5)、式(6)。
[Ko=MdMo=(Fsinθ)L3+GL2(Fcosθ)L1] (5)
[Kc=f'G+c'A'H] (6)
式中:[Md]、[Mo]分别为抗倾和抗覆力矩;F为墙后土压力;θ为土压力方向与水平向夹角;L1为土压力水平分力的力臂、L2土压力竖直分力的力臂、L3为墙自重G的力臂;[G]为挡土墙上垂直水平面荷载的和;[H]为平行墙基荷载的和;f′和c′分别为墙底与基础的摩擦系数和黏聚力。
1.3 挡土墙稳定分析确定性计算
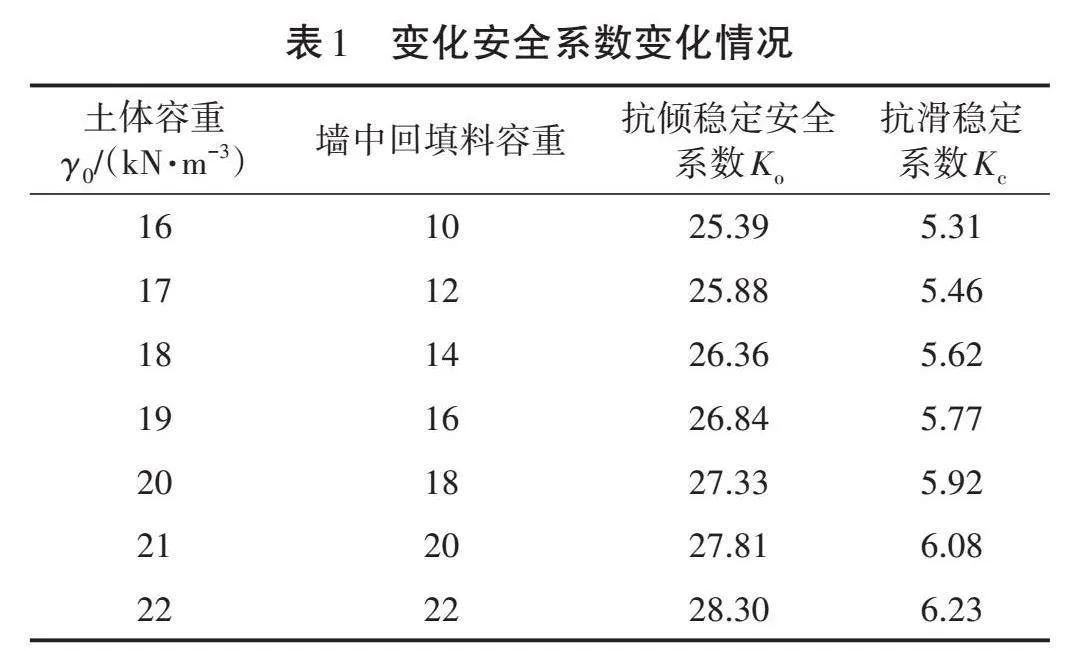
本研究涉及的装配式挡土墙高为5.4 m,墙背填土高4.5 m。研究表明,土体容重、墙中回填料容重、填土内摩擦角及土墙摩擦角是影响挡土墙稳定性的重要因素。土体容重、墙中回填料容重、填土内摩擦角等参数见表1、表2[2]。
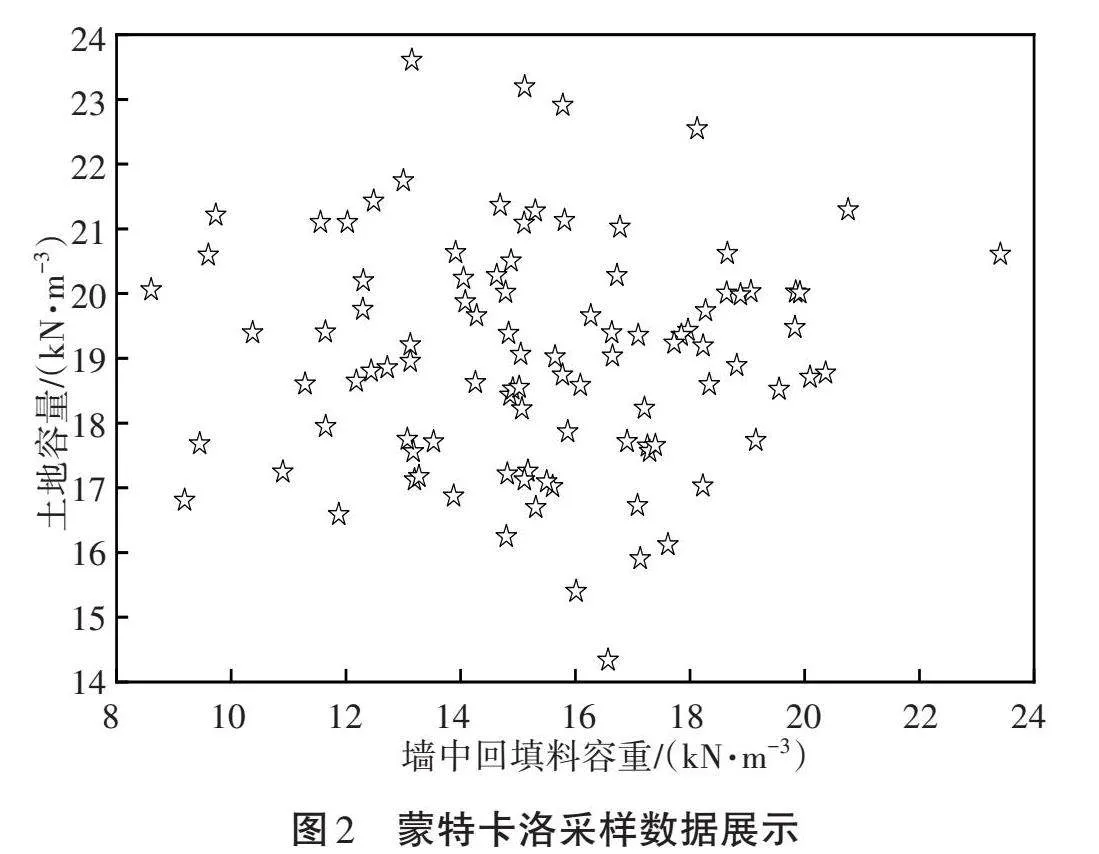
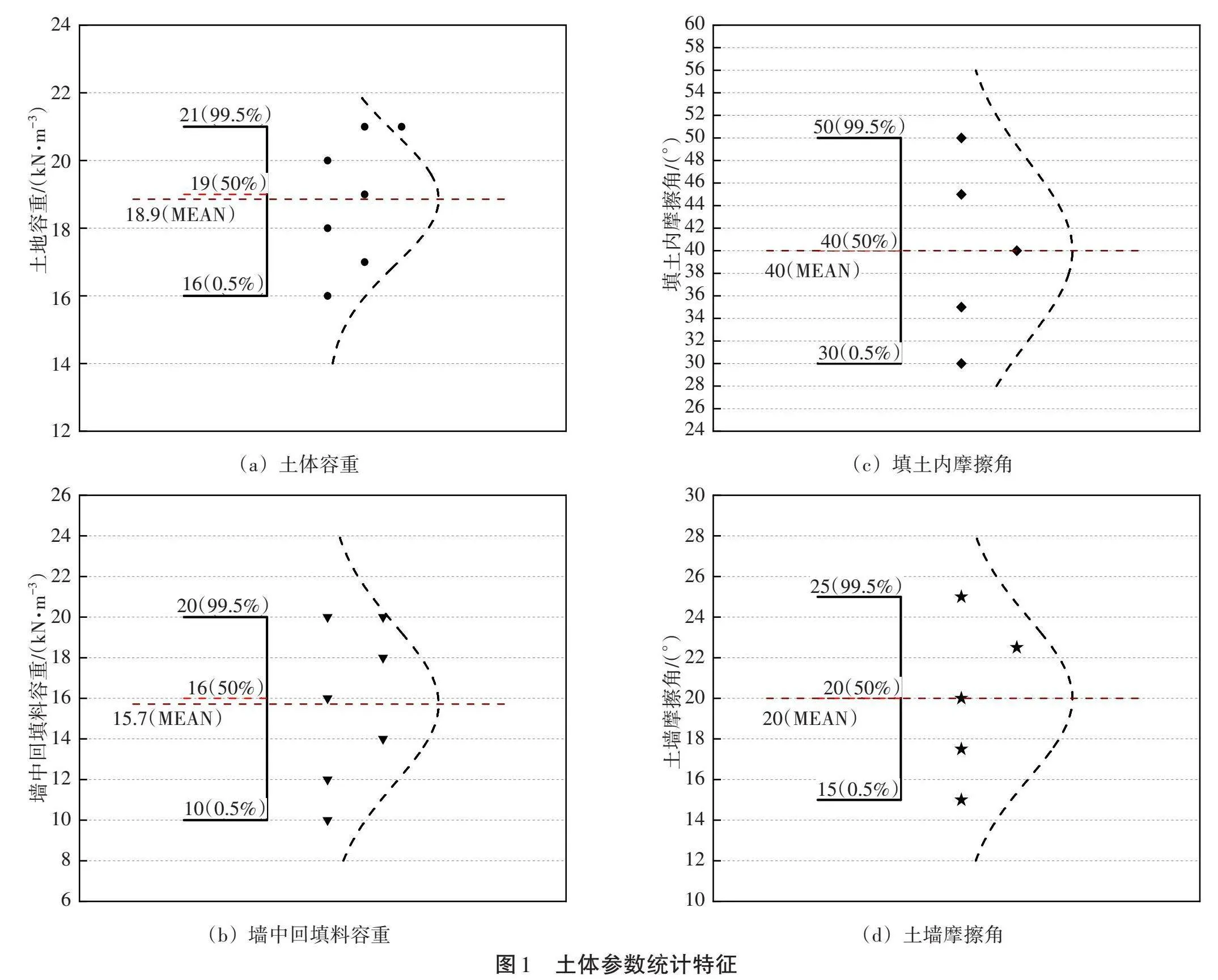
该土体相关参考数据较少,土体相关参数近似正态分布。土体容重近似正态分布N~(18.9,1.55^2),墙中回填料容重近似正态分布N~(15.71,3.05^2),填土内摩擦角近似正态分布N~(40,7.07^2),土墙摩擦角近似正态分布N~(20,3.54^2),具体如图1
所示。蒙特卡洛采样生成10 000组数据,以表征土体强度参数不确定性。以土体容重和墙中回填料容重为例,蒙特卡洛采样100次如图2所示,可以看
出土体容重和墙中回填料容重覆盖了参数不确定性区间,能够反映参数随机性。
1.4 BP神经网络代理模型
BP神经网络是经典的机器学习算法。本研究将表2数据作为训练数据,训练基于BP神经网络的代理模型,替代确定性计算。研究表明,机器学习模型的数据预测精度满足工程要求。
BP神经网络正向传播见式(7),f为sigmood激励函数[4]。
[fW1X+B1=VW2V+B2=Y] (7)
式中:[W]1为BP神经网络输入层到隐藏层的权值矩阵;B1为隐藏层阈值向量;[W]2为隐藏层到输出层权值矩阵;B2为输出层阈值向量;X为输入向量;Y为输出向量;V为隐藏层输出值向量。
反向传播函数见式(8)。
[E=12Ms=1nk=1ysk-osk2] (8)
式中:M为训练样本数量;n为输出层节点个数;[osk]为样本s在第k个节点的输出期望;[ysk]为第k个节点输出。
2 可靠性分析和参数敏感性分析
2.1 可靠性分析
本研究以抗滑稳定安全为例,介绍基于BP神经网络代理模型的可靠性分析。相关规范要求抗滑稳定系数规范值不小于1.6,构造挡土墙抗滑稳定功能函数见式(9)。
[Z=Kc-1.6] (9)
将1.2节中10 000组参数带入训练好的BP神经网络中,得到10 000个Z值并进行统计,如图3所
示。可以看出,Z值符合正态分布,通过式(10)计算可靠性[5],得到可靠性指标[β]为6.1,远大于规范值一类破坏Ⅲ级规范值2.7。同理,构造挡土墙抗倾安全稳定计算得到可靠性指标[β]为7.5,大于规范值2.7。可见新型装配式挡土墙有较高的安全富余,该挡土墙有优化空间。
[β=μzσz] (10)
2.2 参数敏感性分析
采用Sobol指数法分析因素敏感性,包括土体容重、墙中回填料容重、填土内摩擦角及土墙摩擦角。假设函数f(x)在定义域可积,变量x服从[0,1]区间均匀分布,则f(x)见式(11)、式(12)。
[f(x)=f0+nj=1 n i1<…<ijfi1…ijxi,…,xij] (11)
[f(x)=f0+ifixi+i<jfijxi,xj+…+i<jf1,2,…,nx1,x2,…,xn] (12)
式中:[1⩽i1<…<ij⩽n (1⩽j⩽n)]。
设f(x)满足前置条件[01fi1…ijxi,…,xijdxk=0],[k=i1,…,ij],可将函数f(x)的总方差分解为式(13)。
[D=iDi+i<jDij+…+D1,2,…,n] (13)
式中:D为f(x)总体方差;[Di]为第i个参数的方差;[Dij]为第i、j个参数相互作用的方差;[D1,2,…,n]为n个参数共同作用下所产生的方差。
若各参数间作用敏感系数满足式(14),则敏感系数的计算见式(15)至式(17)。
[iDiD+i<jDijD+…+D1,2,…,nD=1] (14)
[SCi=Di/D] (15)
[SCij=Dij/D] (16)
[SCTi=1-D∼i/D] (17)
式中:变量xi的敏感系数用SCi表示;变量 xi和xj相互作用敏感系数用SCij表示;考虑变量xi和其他相关参数共同作用敏感系数用SCTi表示;其他参数产生的方差用D~i表示。
通过Sobol指数法计算输入参数或输入参数集合对输出方差的贡献,以确定参数在模型中具有的影响。填土内摩擦角Sobol指数为0.65,明显高于土墙摩擦角Sobol指数0.17,土体容重和墙中回填料容重Sobol指数为3Ghc53B8pWNy7W5Y7c97Cg==0.11和0.07。综上所述,对新型挡土墙稳定性影响强弱排序为填土内摩擦角>土墙摩擦角>土体容重>墙中回填料容重。
3 结论
①BP神经网络代理模型能够较好地替代新型挡土墙稳定性计算过程,能够有效减少抗滑稳定计算、抗倾覆计算的计算次数,提高了新型挡土墙稳定性分析的计算效率,可通过较少的计算消耗获得令人满意的计算效率。
②研究的新型装配式挡土墙的抗滑稳定、抗倾安全稳定可靠性指标分别为6.1和7.5,具有较高的安全富余,该挡土墙还有进一步优化设计的空间,传统确定性方法估计挡土墙安全性偏保守。
③参数敏感性强弱排序为填土内摩擦角>土墙摩擦角>土体容重>墙中回填料容重,对填土内摩擦角度的准确测定估计是评价新型装配式挡土墙稳定性的前提,在挡土墙设计过程中应重视。
参考文献:
[1]吴国印,汪魁,易朋莹,等.新型装配式挡土墙稳定性影响因素敏感度分析[J].重庆交通大学学报(自然科学版), 2021, 40(9): 92-100.
[2]刘云龙,张道兵,张标,等.基于孔隙水效应的多失效模式下挡土墙可靠性分析[J]. 湖南科技大学学报(自然科学版), 2022, 37(1): 1-9.
[3]赵明华,蒋冲,曹文贵.基于区间理论的挡土墙稳定性非概率可靠性分析[J].岩土工程学报, 2008(4): 467-472.
[4]鲍伟,任超.基于GWO-BP神经网络的电池SOC预测方法研究[J].计算机应用与软件, 2022, 39(9): 65-71.
[5]ZHENG Z, LI Y, WEN L, et al. Reliability analysis of an embankment dam slope based on an ellipsoid model and PSO-ELM[J]. Structures, 2023, 55: 2419-2432.

